惩罚广义估计方程在纵向数据基因关联分析中的应用*
曹红艳 曾 平 李 治 崔跃华,4张岩波△
惩罚广义估计方程在纵向数据基因关联分析中的应用*
曹红艳1曾 平2李 治3崔跃华1,4张岩波1△
目的 探讨惩罚广义估计方程(pGEE)在纵向数据基因关联分析的应用,为纵向数据基因关联分析提供方法学参考。方法 以小鼠糖尿病发病相关的数量性状位点识别为例,分别采用广义估计方程(GEE)和pGEE进行分析。结果 pGEE筛选出糖尿病发病关联位点,为分子生物学研究提供了重要的候选位点。结论 pGEE能有效的实现高维纵向数据的变量选择,识别出有意义的关联位点。
惩罚广义估计方程 纵向数据 SCAD 基因关联分析 数量性状位点
随着分子生物学测序技术的不断发展,基因关联分析已经成为了复杂疾病研究的最重要手段之一,成功的识别了多种人类复杂疾病(如Ⅱ型糖尿病,高血压等)的遗传变异位点[1-2]。为了更好地了解复杂疾病和遗传变异之间的关系,越来越多的基因关联分析通过纵向的方式进行,对同一观察对象的某观察指标在不同时间上进行重复测量,数据形式表现为非独立结构。纵向数据基因关联分析相比于横断面研究,可以研究复杂性状随时间变化的关系,从而增强统计效能,提高遗传变异对复杂疾病的解释程度[3-5]。
纵向基因数据和一般的纵向数据相比,更为复杂,高维度,不同SNP之间存在复杂的LD结构,表现为强相关性和多维共线性;同时,大部分的SNP为冗余信息,只有少量的SNP为关联位点且信号强度弱,将导致参数估计和统计推断的准确性和有效性大大降低,高维纵向基因关联分析面临着巨大的挑战。因此,发展新的变量选择方法尤为重要。近年来,基于惩罚的变量选择方法备受关注,如Lasso[6],SCAD[7],自适应Lasso[8]等。惩罚方法能有效地应用于高维数据分析,通过收缩将弱效应估计为0,参数估计和变量选择同时进行,广泛的应用于不同模型的变量选择。经典的纵向数据分析中,广义估计方程(generalized estimating equations,GEE)[9-11]只需定义伪得分方程(quasi -score equations),当作业相关矩阵设置不正确时,仍然能得到一致性的参数估计,在应用中独占优势。因此,Wang,Zhou和Qu发展了基于SCAD的惩罚广义估计方程(penalized generalized estimating equations,pGEE)[12],不仅保持了GEE的重要特性,同时将GEE推广到高维数据分析,适用于协变量个数p随样本例数n同阶变化的情况,即P=O(n)。本文以小鼠的糖尿病发病相关的数量性状位点(quantitative trait locus,QTL)识别为例,进行pGEE分析,识别出小鼠的糖尿病发病相关的QTL,为QTL分析提供方法支持。
资料与方法
1.资料来源
数据来源于2型糖尿病发病相关的QTL遗传研究[13],由于肥胖是2型糖尿病主要危险因素,Reifsnyder等将肥胖且有糖尿病倾向的NZO(new zealand obese)/HILt小鼠与瘦且无糖尿病倾向的NON(nonobese nondiabetic)/Lt小鼠进行远交(outcross),产生的F1代再与亲本NON/Lt小鼠回交(backcross)生成多基因实验小鼠模型。对203例雄性实验小鼠,测量其在4、8、12、16、20、24周的体重,同时,在已知QTL位点周围20 cM范围内的高频标记中,挑选了83个微卫星位点,研究微卫星位点对体重的影响,数据形式如表1所示。

表1 体重和微卫星标记数据集形式
2.方法
(1)广义估计方程
在纵向数据基因关联分析中,设Yit为个体i在时间t的观察值,Xit为p维协变量向量,令Yi=(Yi1,…Yit)T为个体i的观察向量,Xi=(Xi1,…,Xit)T为个体i的协变量矩阵,则纵向数据分析的模型框架可表达如下:
E(Yit)=μi,g(μi)=X′iβ
基于全似然函数的参数估计方法,只有在一些特殊情况下,如当Yit服从多元正态分布时,才能直接算出,对于其他的分布,全似然函数的计算非常复杂。GEE采用类似于广义线性模型的得分方程的方法,定义伪得分方程为:

(2)惩罚广义估计方程
基于惩罚的变量选择方法有很多,Fan和Li指出一个好的惩罚函数估计值应具备无偏性、稀疏性和连续性,即Oracle性质[7]。SCAD惩罚能保留较大的系数,同时将较小的系数收缩为0,具有Oracle性质,其惩罚函数pλ(θ)的导数如下:

其中,I为指示函数,a为预先选择的常数,Fan和Li推荐a=3.7。
对GEE的得分函数进行SCAD惩罚,得到pGEE的惩罚表达式为:

采用minorization-maximization算法得到(2)式的渐进表达式,
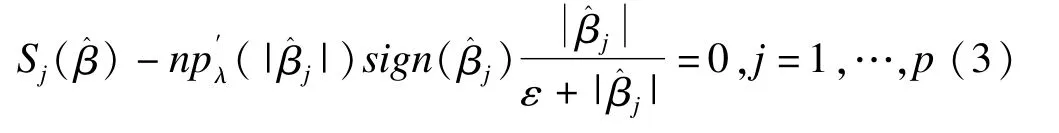
其中Sj(β^)为S(β^)的第j个得分函数,ε的取值较小,一般取ε=10-6。进一步采用New ton-Raphson算法对(3)进行迭代,计算得到pGEE的参数估计值。pGEE估计值依赖于惩罚参数λ,在此,采用交叉验证(cross validation,CV)选择最优λ。
(3)统计分析采用R软件中的“PGEE 1.4”软件包,可实现GEE和pGEE分析,GEE分析也可采用“geepack”包。“PGEE 1.4”包含3个函数:MGEE,CVfit和PGEE。“MGEE”函数用于GEE分析,“CVfit”用于计算交叉验证的最优惩罚参数λ,得到最优λ后,采用“PGEE”函数计算pGEE的参数估计值。适用于测量结果呈正态分布、二项分布、Poisson分布以及Gamma分布的情况,为纵向数据基因关联分析提供了强有力的分析工具。
本例中,以体重为应变量,以83个微卫星位点、测量时间及时间的平方为协变量,共85个协变量,X=[1,time,time2,x1,x2,…,x83],其中xj编码为0和1,这是典型的纵向数据基因关联分析。对所有变量均进行标准化,采用正态链接函数的GEE和pGEE进行分析。由于每只实验小鼠在等距的时间间隔内重复测量了6次,两次测量相隔时间越长,相应的相关关系越小,因此,假定作业相关矩阵为1阶自回归结构。截距项不进行惩罚。通过“CVfit”函数选择出最优的惩罚参数为λ=0.0212,进一步利用“PGEE”函数进行拟合,得到pGEE参数估计结果。GEE分析在“geepack”软件包中实现,GEE和pGEE参数设置均采用软件中的默认设置。
结 果
1.实验小鼠体重一般情况
将每只小鼠的体重测量值按时间进行连接,得体重随时间变化趋势图,如图1。可见小鼠在24周内的个体生长趋势总体上一致,呈先快后慢的趋势,但也存在个体间的差异,个体增长幅度可能不一致,其差别随时间的变化而增加。进一步分析每个微卫星位点的单独效应,对每个位点分别拟合GEE,得到单个位点的效应系数,如图2,单个位点系数分布在[-0.176,0.099]之间,大部分位点的效应非常弱。

图1 小鼠不同周次体重变化趋势图

图2 单个QTL系数图
2.GEE和pGEE分析
在考虑了时间效应的情况下,观察GEE和pGEE对83个微卫星位点的参数估计散点图(图3),pGEE将大部分具有微弱效应的位点收缩为0,有效的进行了降维,而未惩罚的GEE却不满足稀疏性。GEE采用Wald卡方检验进行统计推断,选出了14个有意义的QTL(检验水准),pGEE筛选出11个QTL,其参数估计结果见表2。比较两方法共同筛选出的QTL参数估计值,可看出pGEE估计值明显小于GEE,从QTL效应的微弱性而言,pGEE估计出的QTL效应更符合分子生物学特点。

图3 83个微卫星位点的GEE和pGEE参数估计散点图
在pGEE筛选出的11个QTL中,根据每个QTL系数的正负,认为D1M it211,D5M it158,D6M it275及D15M it29的突变为危险因素,将导致小鼠肥胖,其余7个QTL的变异对小鼠肥胖具有保护效应。
肥胖与2型糖尿病的发病显著相关,将诱发糖尿病的发生。肥胖的发生、发展受多个微效基因及其复杂的交互作用控制,同时也受环境因子的调控,是一种复杂的多因素、多基因疾病[14]。本例中通过pGEE分析筛选出的QTL,和Reifsnyder采用单因素方差分析和置换检验识别的体重相关的7个第一染色体位点相比[13],共同识别的位点为D1M it211,D1M it411,D1M it76。陈峰采用线性混合效应模型(linear mixed model,LMM)的Lasso和SCAD惩罚对小鼠体重QTL进行了识别[15],分别识别出14和3个QTL,和本文结果相比较,基于Lasso的LMM、基于SCAD的LMM以及本文的pGEE,三种不同惩罚模型共同识别出了D1M it411和D5M it158位点,提示这两个位点的重要性,同时pGEE识别的其他9个QTL,也将为糖尿病发病相关QTL分子生物学研究提供重要的候选位点。

表2 GEE和pGEE参数估计值
总之,pGEE成功的对高维纵向基因数据进行了降维,其参数估计具有oracle性质,有效的实现了高维纵向基因数据的变量选择,筛选出了有意义的遗传变异。
讨 论
pGEE分析借助作业相关矩阵考虑了不同时间点测量值之间的内部相关关系,通过基于SCAD的惩罚方法,实现了高维纵向数据的变量选择。本文以糖尿病纵向数据的QTL分析为例,识别出糖尿病发病相关的QTL,说明了pGEE在纵向数据基因关联性分析中应用的科学性和可行性。
基于Wald卡方检验的GEE统计推断,其前提是在保证其他变量不变的情况下,估计变量的偏效应,当维度较高且样本量较小时,基于偏效应的统计推断无法揭示变量的真实效应。基于惩罚的方法参数估计和变量选择同时进行,pGEE中采用的SCAD惩罚具有一致性和oracle性质,保证了非零系数变量的正确推断和选择。在高维纵向基因关联分析中,pGEE的变量选择明显优于GEE的参数估计和统计推断。
pGEE变量选择的一致性和稀疏性依赖于惩罚参数的选择,基于交叉验证的惩罚参数选择方法容易出现过拟合,从而将无效变量选为有意义的变量,出现错误选择[16]。Hyunkeun等通过数据模拟和真实数据分析,指出基于贝叶斯信息准则(bayesian information criterion,BIC)的惩罚参数选择方法得到的参数估计值具有一致性[17]。因此,今后可进一步研究pGEE框架下的BIC惩罚参数选择方法,选择出最优的惩罚参数,以得到更为确切的变量选择结果。需要注意的是,经pGEE筛选出的有意义的位点,还需要结合分子生物学实验进一步验证其生物学意义。
总之,pGEE作为纵向数据经典方法GEE的惩罚模型,一方面,延续了GEE在纵向数据分析中的重要优势:只需设定一阶和二阶矩以及作业相关矩阵,避免了高维纵向数据分析中更为复杂的全似然函数计算;当作业相关矩阵指定不当时,仍能保持参数估计的一致性。另一方面,pGEE将GEE推广到高维数据分析,既能考虑纵向数据之间的相关关系,又能有效的进行降维,识别出高维纵向基因数据的关联位点,为高维纵向数据分析提供了强有力的分析方法。随着分子生物学技术成本的降低,纵向基因数据必将日益增多,pGEE将在纵向数据基因关联性分析中发挥及其重要的作用。
[1]M ccarthy M I,Zeggini E.Genome-w ide association studies in type 2 diabetes.Curr Diab Rep,2009,9(2):164-171.
[2]Ehret GB.Genome-w ide association studies:contribution of genom ics to understanding blood pressure and essential hypertension.Curr Hypertens Rep,2010,12(1):17-25.
[3]Sitlani CM,Rice K M,Lum ley T,et al.Generalized estimating equations for genome-w ide association studies using longitudinal phenotype data.Stat Med,2015,34(1):118-130.
[4]Furlotte NA,Eskin E,Eyheramendy S.Genome-w ide association mapping w ith longitudinal data.Genet Epidem iol,2012,36(5):463-471.
[5]ShiG,Rao D.Ignoring temporal trends in genetic effects substantially reduces power of quantitative trait linkage analysis.Genetic epidem iology,2008,32(1):61-72.
[6]Tibshirani R.Regression shrinkage and selection via the lasso.Journal of the Royal Statistical Society.Series B(Methodological),1996:267-288.
[7]Fan J,Li R.Variable selection via nonconcave penalized likelihood and its oracle properties.Journal of the American statistical Association,2001,96(456):1348-1360.
[8]Zou H.The adaptive lasso and its oracle properties.Journal of the A-merican statistical association,2006,101(476):1418-1429.
[9]Liang KY,Zeger SL.Longitudinal data analysis using generalized linearmodels.Biometrika,1986,73(1):13-22.
[10]陈启光.纵向研究中重复测量资料的广义估计方程分析.中国卫生统计,1995,12(1):22-25.
[11]李洪艳,谭珊,高晓,等.基于广义估计方程的婴儿超重的影响因素分析.中国卫生统计,2016,33(2):222-225.
[12]Wang L,Zhou J,Qu A.Penalized generalized estimating equations for high-dimensional longitudinal data analysis.Biometrics,2012,68(2):353-360.
[13]Reifsnyder PC,Churchill G,Leiter EH.Maternal environment and genotype interact to establish diabesity in m ice.Genome Res,2000,10(10):1568-1578.
[14]Reifsnyder PC,Leiter EH.Deconstructing and reconstructing obesityinduced diabetes(diabesity)in m ice.Diabetes,2002,51(3):825-832.
[15]陈峰.线性混合效应模型的惩罚变量选择.中国卫生信息管理杂志,2014,11(3):278-284.
[16]Wang H,Li R,Tsai CL.Tuning parameter selectors for the smoothly clipped absolute deviation method.Biometrika,2007,94(3):553-568.
[17]Cho H,Qu A.Model selection for correlated data with diverging number of parameters.Statistica Sinica,2013,23:901-927.
(责任编辑:张 悦)
The Application of Penalized Generalized Estimating Equations in Genetic Association w ith Longitudinal Data
Cao Hongyan,Zeng Ping,Li Zhi,et al(Department of Health Statistics,ShanxiMedical University(030001),Taiyuan)
Objective To explore the application of penalized generalized estimating equations(pGEE)in genetic association w ith longitudinal data,and provide new statistical solutions for longitudinal genetic data analysis.M ethods We applied the generalized estimating equations(GEE)and pGEEmethods to a type II diabetes dataset for quantitative trait locus identification.Results Several loci associated w ith the development of type IIdiabeteswere identified using the pGEEmethod,providing important candidatemakers for further biological validation.Conclusion The pGEEmethod provides a powerful tool for high dimensional longitudinal genetic association studies.
Penalized generalized estimating equations;Longitudinal data;SCAD;Genetic association studies;Quantitative trait locus
*:国家自然科学基金资助项目(30972553,31371336)
1.山西医科大学卫生统计教研室(030001)
2.徐州医科大学流行病与卫生统计学教研室
3.中北大学体育学院
4.美国密西根州立大学统计与概率系
△通信作者:张岩波,E-mail:sxmuzyb@126.com

