溜井放矿冲击气流流场数值模拟研究
汤民波,姚贵佳,李义杰,陈 亮
(1.湖南有色金属职业技术学院, 湖南 株洲 412000; 2.江西瑞林稀贵金属科技有限公司, 江西 宜春 336000; 3.江西理工大学, 江西 赣州 341000)
综合技术
溜井放矿冲击气流流场数值模拟研究
汤民波1,姚贵佳2,3,李义杰3,陈 亮3
(1.湖南有色金属职业技术学院, 湖南 株洲 412000; 2.江西瑞林稀贵金属科技有限公司, 江西 宜春 336000; 3.江西理工大学, 江西 赣州 341000)
为了认识溜井卸矿冲击气流的基本规律及有效控制溜井粉尘污染,基于流体力学对溜井卸矿时冲击气流形成过程进行理论分析,推导出冲击气流与卸矿高度关系式。运用FLUENT模拟分析了溜井卸矿过程中的冲击气流流场分布、压力场分布以及各个溜井口产生的气流随时间的变化,结果表明:溜井放矿过程中,放矿体前端正压和后端负压力值不断增加,溜井内的活塞效应明显;溜井内部气流流场可分为涌入气流区域、反向气流区域、涡流区域、冲击气流区域;随着放矿体下落,各支岔溜井口依次产生最大的冲击气流,并且随着放矿高度的增大而增加。
溜井; 冲击气流; 流场; 数值模拟
1 前言
随着井下机械化程度的提高,矿山通过溜井的矿石量大大增加,所以大断面、高落差的溜井成为今后溜井系统的发展趋势[1]。溜井卸矿时由于受到溜井细长空间的限制,溜井内的空气在下落的破碎矿石的压缩下,形成类似于活塞的运动,卸矿高度的增加使溜井内的空气急剧压缩并产生更大的动压,进而生成更加强大的冲击风流,风流夹带着粉尘通过支岔溜井和卸矿硐室形成更大范围的扩散,严重污染卸矿硐室及周围巷道,甚至污染整个通风系统[2~5]。为了认识溜井冲击气流的基本规律及有效控制溜井粉尘污染,基于流体力学原理,对冲击气流形成过程进行理论分析,并根据分析结果进行数值模拟研究。
2 溜井放矿冲击气流理论
2.1 溜井放矿物理模型与假设
真实的溜井系统卸矿是一个复杂的过程,首先溜井系统(尤其是高溜井系统)的特点是断面小、细长,溜井主体与多个中段的支岔溜井口相连;并且溜井矿石下落过程中会与溜井壁碰撞或矿石与矿石之间相互碰撞,矿石下落过程是不规则的加速运动,在这样的环境中产生的空气动力学问题非常复杂,由于矿石下落的高速性及空间的约束性,溜井冲击气流的研究与航空及列车进出站的动力学研究有很多相似之处,同时也有很大的差异。
矿石在下落过程中,速度时刻都在增大,在放矿体后端形成的负压不断增大,形成诱导风流,溜井外的气体由上方井口进入溜井内。同时放矿体下方压力不断升高,形成活塞风流,其中因为下部溜井口压力小于溜井内压力,小部分气体被挤推继续沿溜井向下,而大部分气体从支岔溜井口冲出形成冲击气流,并随之带出大量的粉尘,从而对整个井下通风系统产生影响和污染,溜井内活塞风流场与矿石下落速度的关系具体情况如图1所示,矿石下落瞬时速度为Vt,矿石后侧溜井内风流流速为V0,支岔溜井口冲击气流风速为V1,支岔溜井口下方气流风速为V2,定义垂直向下的方向为速度的正方向。
2.2 溜井放矿冲击气流计算模型
根据流体力学原理可知,空气绕过放矿体流动为绕流运动。图2中,将每次放矿的矿石作为一个分散的整体,称之为放矿体,简化为一个长方体,V0为放矿体下落的速度,S0为放矿体的横断面积,l0为放矿体的整体特征长度,S为溜井断面面积,V为巷道内活塞风速,W为放矿体与溜井壁之间的环状空间中气流对于巷道壁的速度,S1为支岔口断面积,V1为支岔口冲击气流速度。在dt时间内,放矿体在溜井内排开的空气体积为S0V0dt,而在放矿体下方,部分空气被放矿体推动向下运动,总体积为SVdt,放矿体经过支岔口时,体积为S1V1dt气体从溜井口冲出,形成冲击气流,剩余气体部分继续向下,部分通过放矿体与井巷壁之间的环状空间逆向流走,其体积为(S-S0)Wdt。根据气体流动的连续性方程可得[6~10]:
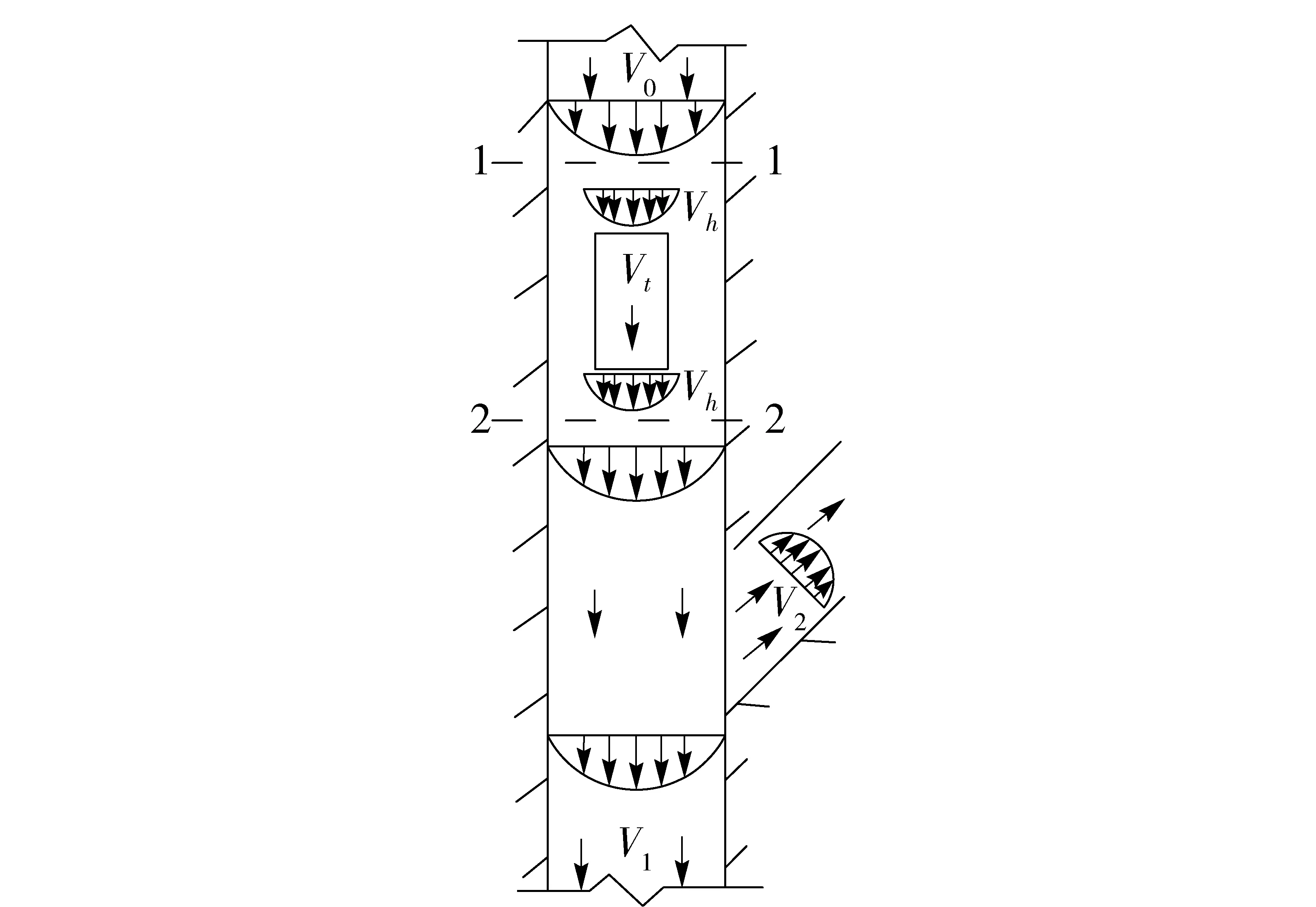
图1 矿石在溜井中下落的活塞风模型图
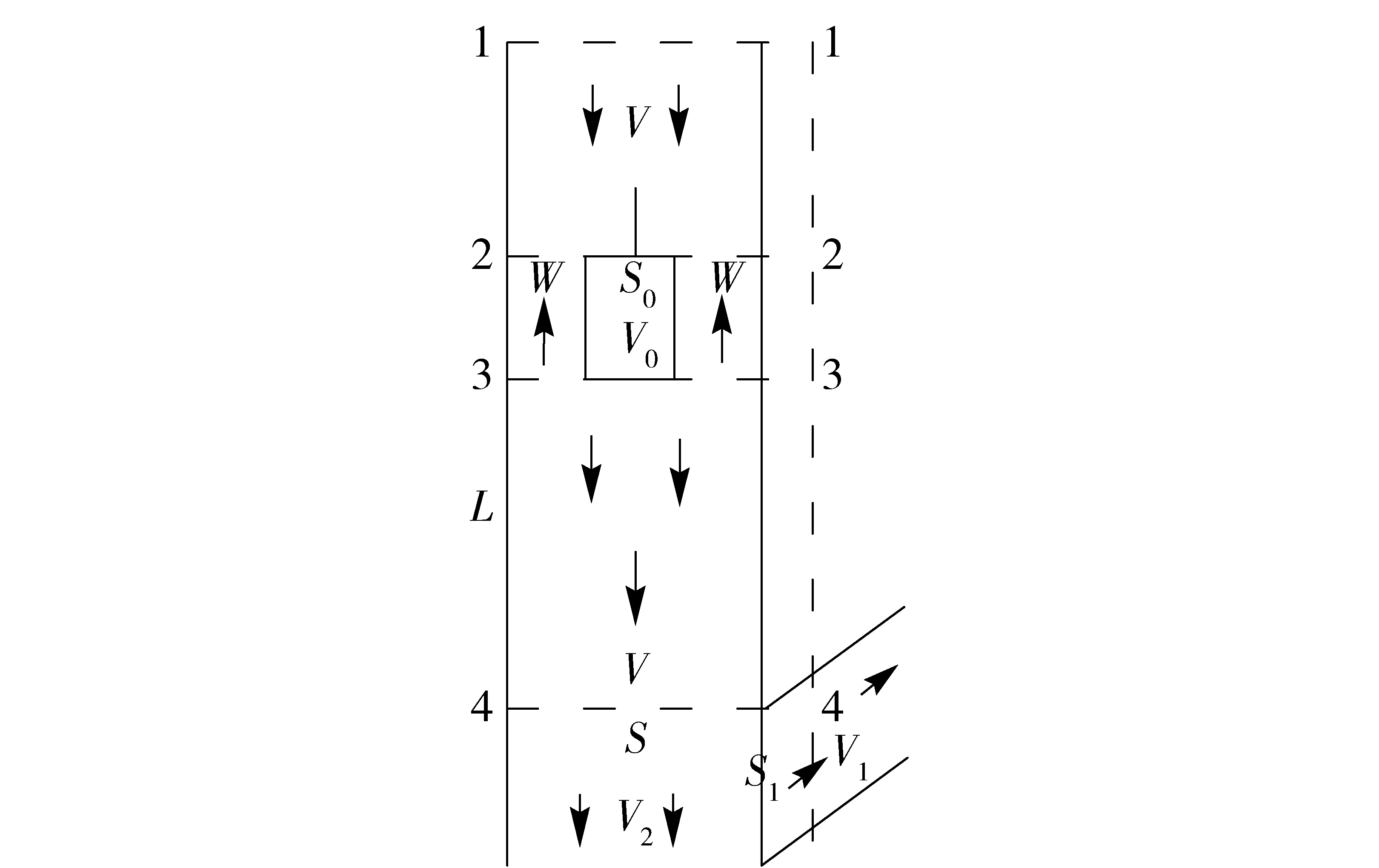
图2 放矿体在溜井中下落的简化计算模型
S0V0dt=SVdt+(S-S0)Wdt
(1)
且SVdt=S1V1dt+SV2dt
(2)
在放矿体与溜井壁之间的环状空间中向放矿体上方流动的气流相对于放矿体的速度为:
(3)
式中:α——放矿体相对溜井的阻塞比。
矿石从高处坠落在重力作用下速度越来越快,根据伯努利方程,由溜井内断面2—2与断面3—3之间气流相对放矿体运动的伯努利方程为:
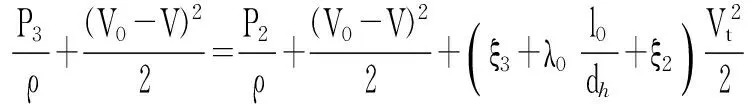
(4)
将式(3)代入上式,可得:
(5)
式中:P3——放矿体下落前方压力,Pa;
P2——放矿体下落后方压力,Pa;
ξ3——气流由放矿体下方溜井段进入环状空间的进口局部阻力系数;
ξ2——反向气流进入放矿体上方溜井出口局部阻力系数;
λ0——反向气流的沿程阻力系数,kg/m3;
l0——放矿体的高度,m;
dh——环状空间水力直径,m;
ρ——空气密度,kg/m3。
根据放矿体气候伯努利方程可得:
(6)
式中:ξ1——溜井井口的局部阻力系数;
λ——溜井沿程阻力系数,kg/m3;
l12——放矿体的后方距离溜井口的长度,m;
l34——放矿体的前方距离溜井口的长度,m;
l——溜井高度,m;
d——溜井水力直径,m。
式(6)与式(5)对比可得:
(7)
根据伯努利方程:
(8)
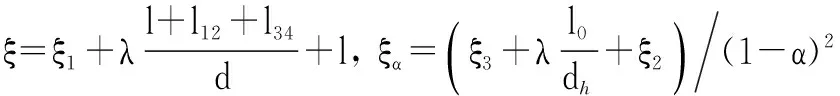
则式(8)可简化为:
ξV2=ξα(V0-V)2
(9)
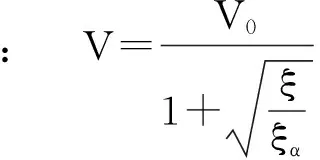
(10)
由于矿石在溜井内做落体运动(忽略摩擦撞击影响),因此:
(11)
式中:H——卸矿高度,m。
将公式(10)、(11)代入(2)可得支岔溜井口风速为:
(12)
矿石下落过程中放矿体前后的压力分布:
(13)
由此可知,当放矿体在溜井内做落体运动时,支岔溜井口冲击气流大小与卸矿高度有关[11];且放矿体前端压力始终高于放矿体后端压力,放矿体前后压力差随卸矿高度的增加而增大,进而影响溜井冲击气流风速大小。
3 溜井放矿冲击风流数值模拟结果及分析
3.1 几何模型及边界条件
溜井为直径4m圆柱体,溜井高度为250m,每50m为一个中段,每个中段有支岔溜井口与溜井相连,假设每次放矿所有矿石为一个分散的整体,整体直径为2.5m,矿石下落加速度为9.8m/s2,入口边界为压力入口在井筒上方,出口边界为压力出口在井筒下方各支岔溜井口。溜井内为不可压缩气流。
3.2 模拟实验及分析
3.2.1 各时间点压力云图
分别提取在放矿体下落过程中1、2.6、4、5、5.9、6.5s和6.9s等7个相对具有代表性时刻的溜井内压力场分布,并以溜井中轴线为路径分布50个监测点监测各时刻溜井内压力,并截取z=0截面放矿体前后压力分布图,如图3和图4。

图3 1~5s时放矿体前后溜井内压力云图
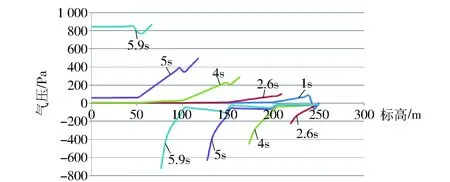
图4 1~5s时溜井内压力散点分布曲线
从图3和图4可以看到在溜井放矿过程中,随着放矿体下落速度的增加,放矿体前端正压和后端负压力值不断增加,并且影响范围越来越大,放矿体前后的压力差愈来愈大,因此溜井内的活塞效应愈加明显,下部支岔溜井的冲击气流将会越来越大。由图4看到在4s这条曲线上,溜井内放矿体前后压力差超过800Pa,到达5.9s时压力差达到1.6kPa。此时也是底部支岔溜井口冲击气流最强烈的时候。
从图5和图6可以看到,在溜井放矿过程中6.5s和6.9s时,放矿体下落到+50m以下,因其下部没有出口,所以气流从放矿体侧面冲出形成反向气流,可以看到放矿体下方的溜井内正压力在短时间内急剧增加,达到3~4kPa,而且几乎分布于整个下部溜井内,而于放矿体后端负压相对前端正压要小很多,而且负压范围要小很多,但总体来看,在这一时刻溜井内放矿体前后压力差达到6kPa。另外由于反向气流向上冲出,使放矿体后端小范围内气压上升,在+100m标高和+50m标高处溜井内均为正压。
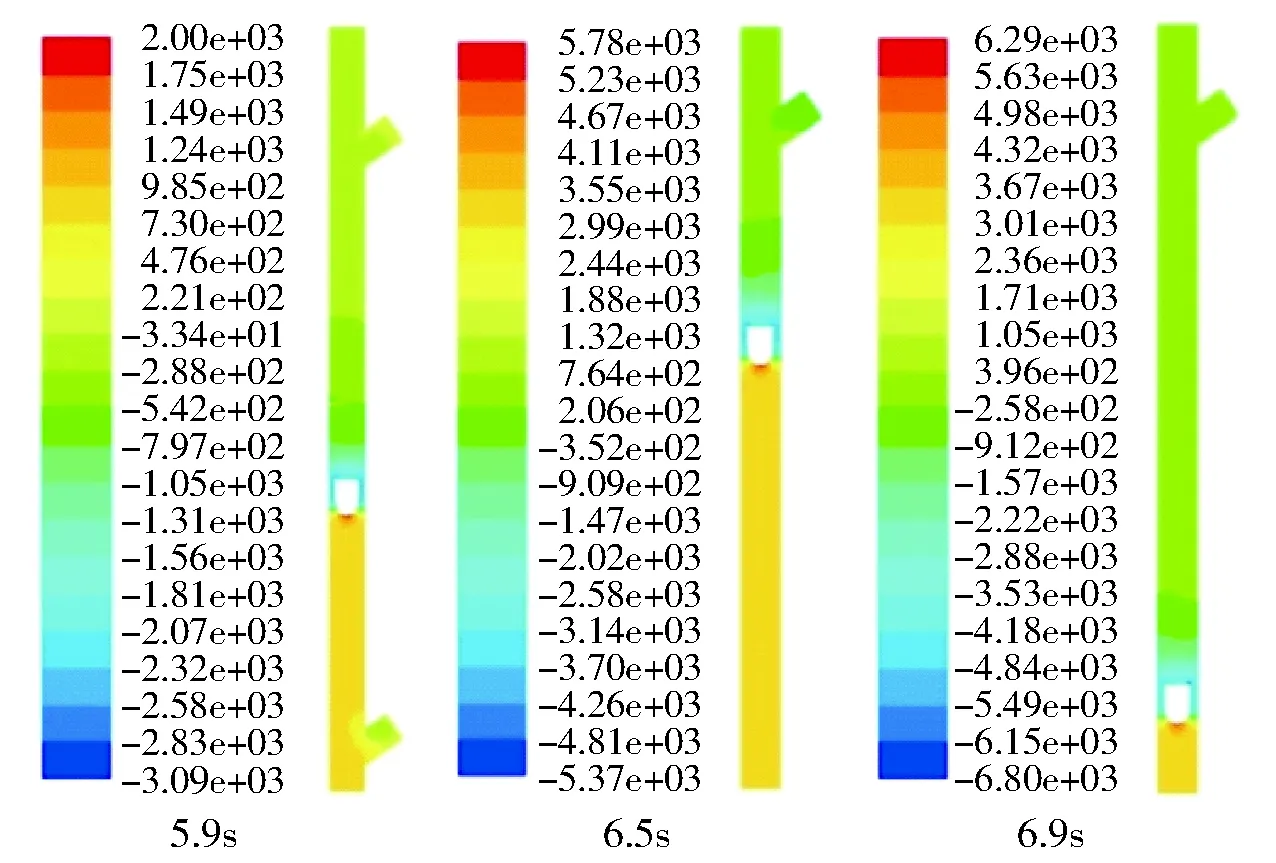
图5 5.9~6.9s时放矿体前后溜井内压力云图
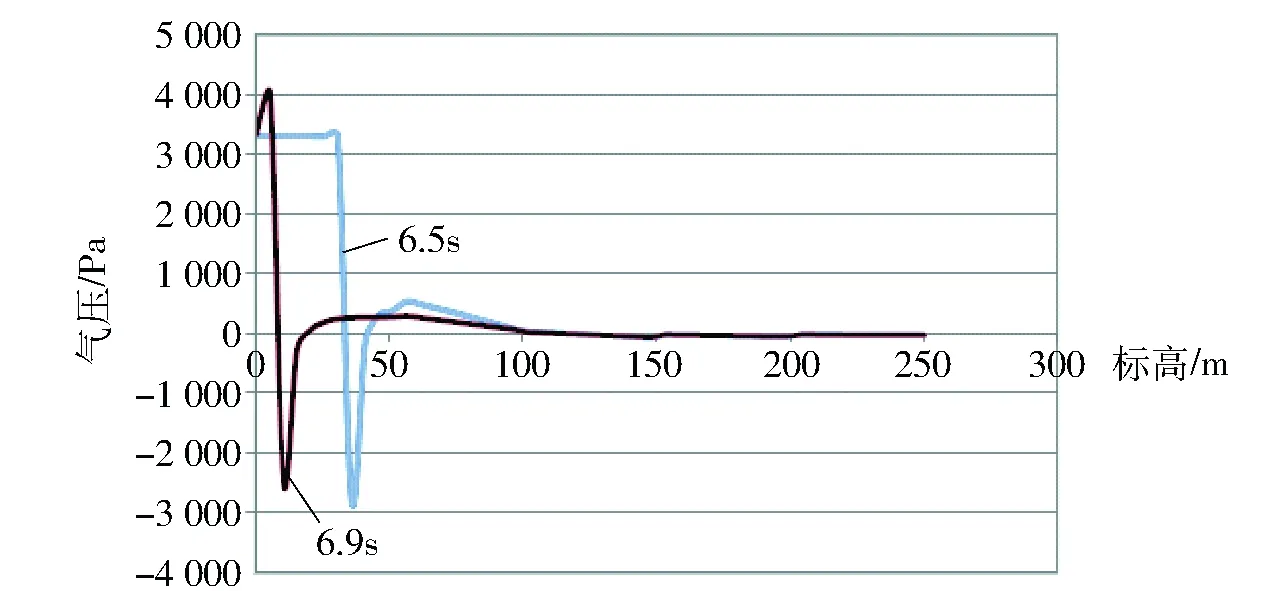
图6 6.5、6.9s时溜井内压力散点分布曲线
3.2.2 各时间点速度云图
分别提取1、2.6、4、5、5.9、6.5s和6.9s等7个相对具有代表性的时间点时溜井冲击气流流场分布数据,并且截取了z=0时刻各溜井口速度云图,如图7至图13所示。
(1)1s时刻速度云图及流场图。由图7可以看出,放矿体在下落1s时,放矿体正处于+200m标高以上较远处,溜井内放矿体下方压力开始增加,在+200m标高溜井口开始形成气流,风速大概在1m/s左右;同时放矿体后端开始产生负压。
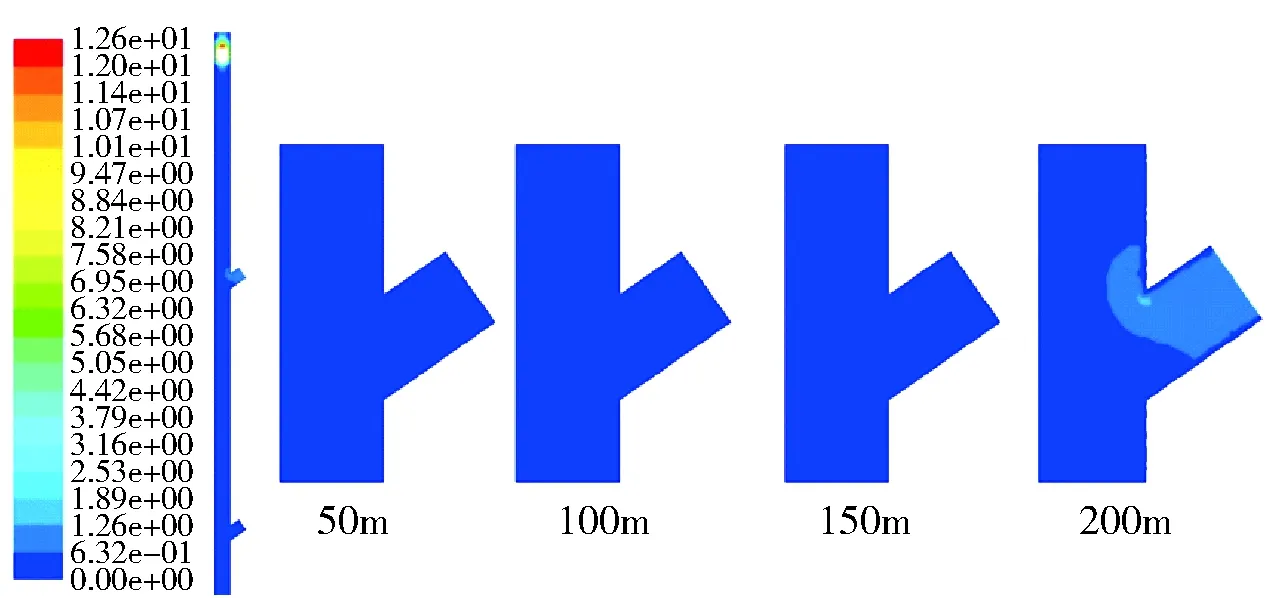
图7 z=0时刻各溜井口速度云图(1s)
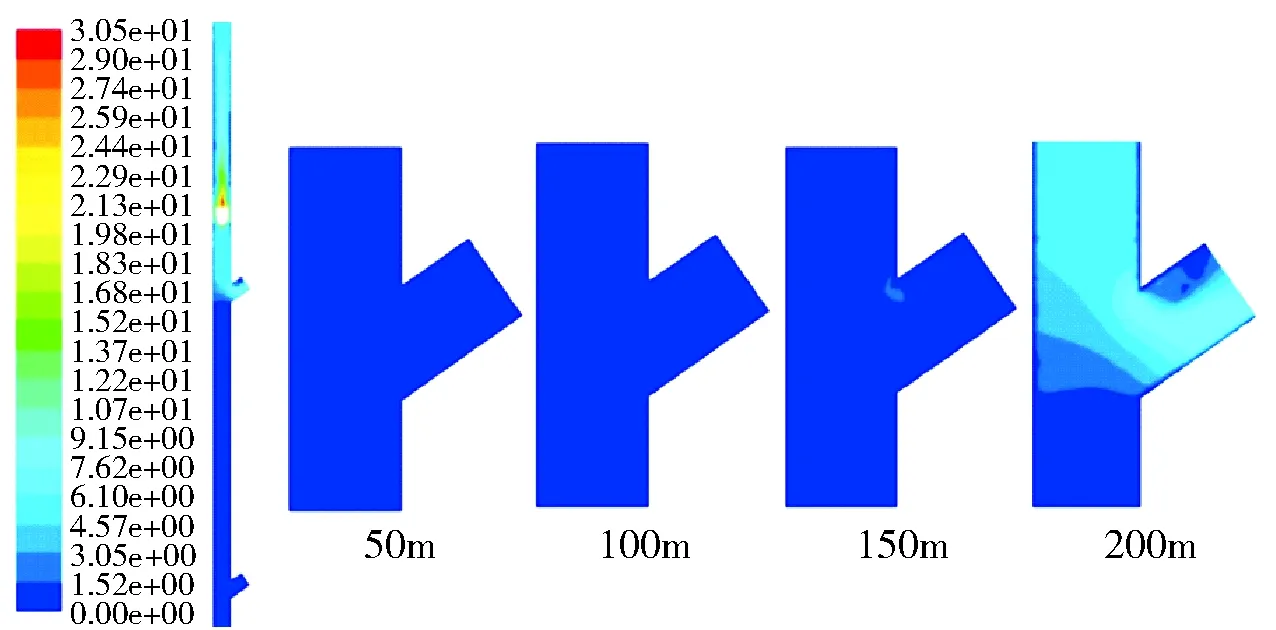
图8 z=0时刻各溜井口速度云图(2.6s)
(2)2.6s时刻速度云图及流场图。由图8可以看出,放矿体在下落2.6s时,放矿体正处于+200m标高上方附近,+200m标高溜井口冲击气流明显加大,达到约9m/s,+150m溜井口气流受到上部放矿体影响,产生气流。
(3)4s时刻速度云图及流场图。由图9可以看出,放矿体在下落4s时,放矿体下落至+200m标高至+150m标高之间,此时+150m标高溜井口产生的冲击气流较2.6s时速度明显增大,达到约16m/s,同时在+100m标高溜井口开始产生气流,风速也达到3m/s,溜井口支岔溜井转弯内侧均产生明显涡流区域,而在+200m标高的溜井口,此时产生涌入的气流,风速大概为6m/s。
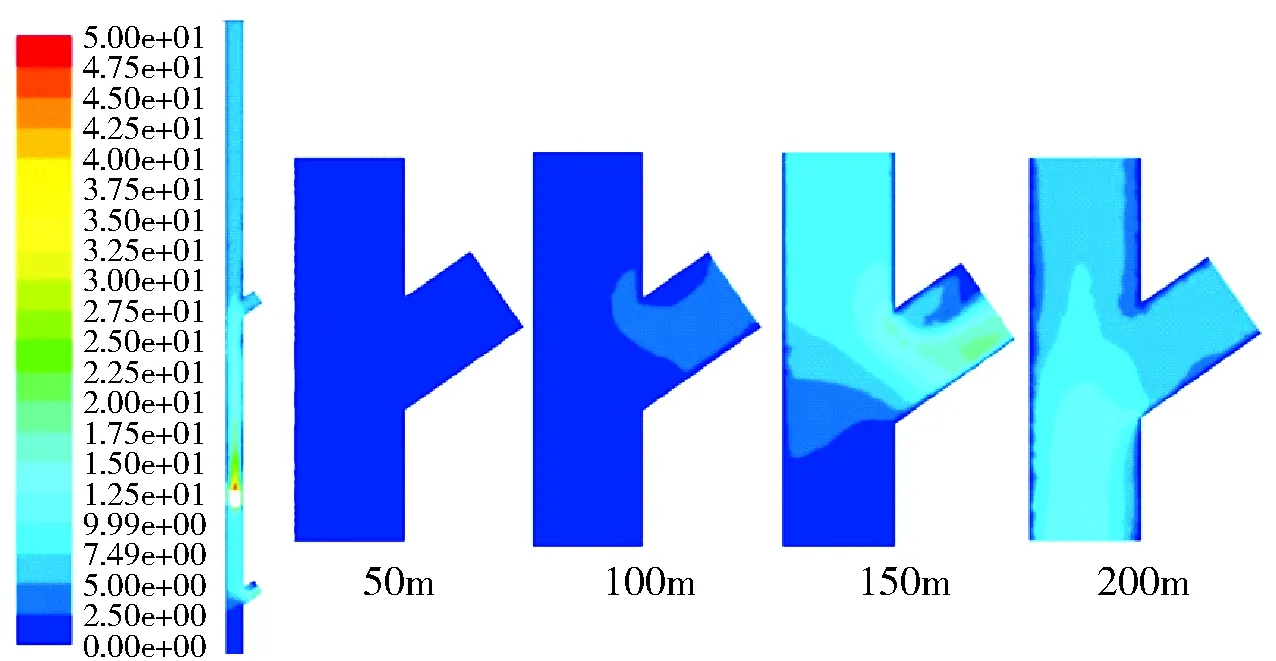
图9 z=0时刻各溜井口速度云图(4s)
(4)5s时刻速度云图及流场图。由图10可以看出,放矿体在下落5s时,放矿体下落至+150m标高至+100m标高之间,此时+50m标高支岔溜井口开始产生气流,风速约为5m/s,+100m标高溜井口冲击风流最大,达到约23m/s。同时+150m标高和+200m标高溜井口产生涌入气流,风速约为6m/s,在+150m标高支岔溜井下侧拐角处产生涡流区域。
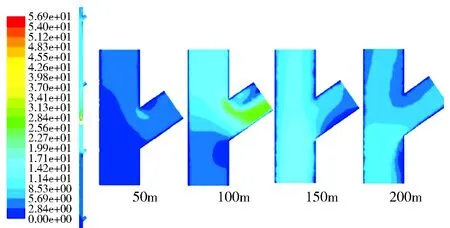
图10 z=0时刻各溜井口速度云图(5s)
(5)5.9s时刻速度云图及流场图。由图11可以看出,放矿体在下落5.9s时,放矿体下落至+100m标高至+50m标高之间,此时冲击风流最大的是+50m标高支岔溜井口,风速达到约33m/s。+100m以上的3个支岔溜井均产生涌入气流,+150m标高和+200m标高溜井口风流较稳定,风速在约5~6m/s。
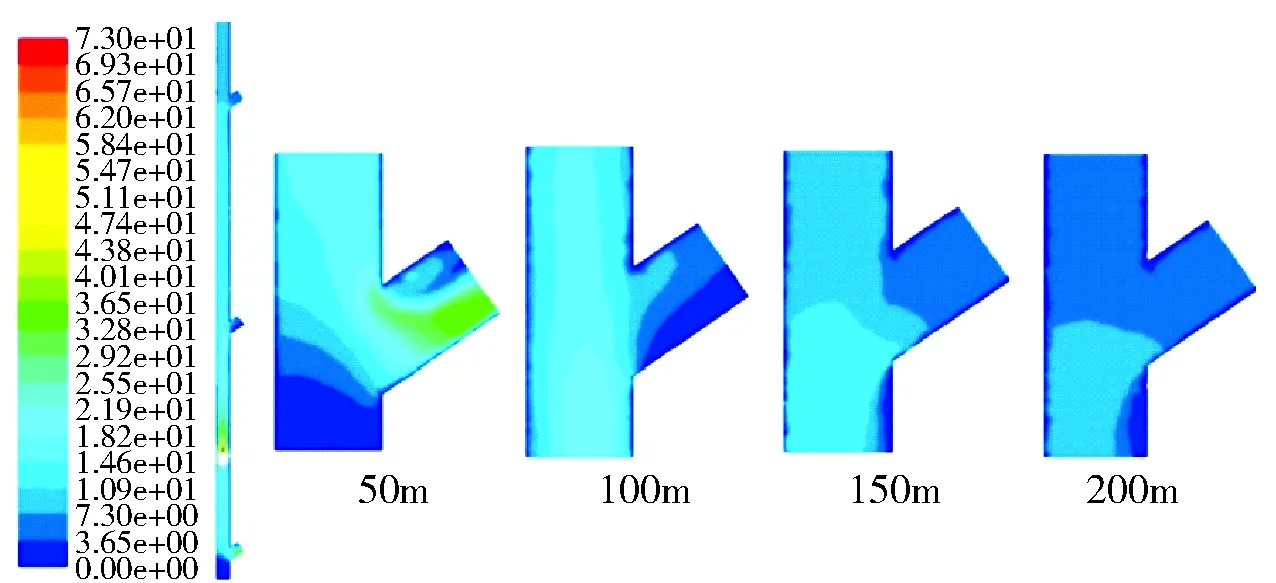
图11 z=0时刻各溜井口速度云图(5.9s)
(6)6.5s时刻速度云图及流场图。由图12可以看出,放矿体在下落6.5s时,放矿体下落至+50m标高以下,此时+50m标高溜井口冲击气流最大,达到约23m/s,较5.9s时风速有所下降,该处冲击风流的组成中一部分为在+50m标高以下的溜井内产生反向的冲击气流,另一部分为从上部溜井口涌入的气流。此时,由于受反向气流影响,溜井内放矿体后侧压力有所升高,所以+100m标高溜井口气流由涌入气流转变为冲击气流,风速为1.5m/s。
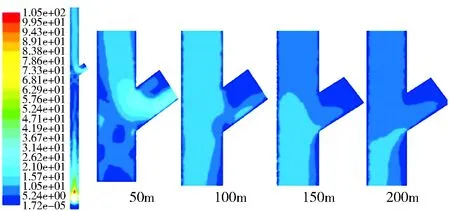
图12 z=0时刻各溜井口速度云图(6.5s)
(7)6.9s时刻速度云图及流场图。由图13可以看出,放矿体在下落6.9s时,放矿体到溜井最底部,已停止运动,此时+50m标高溜井口冲击气流最大达到约22m/s。由于在+50m标高以下的溜井内气流反向,溜井内气压不断增大,+100m标高溜井口风速约4m/s,上部溜井口的涌入风流基本开始稳定,约在4m/s,气流分布规律与6.5s时基本相似。
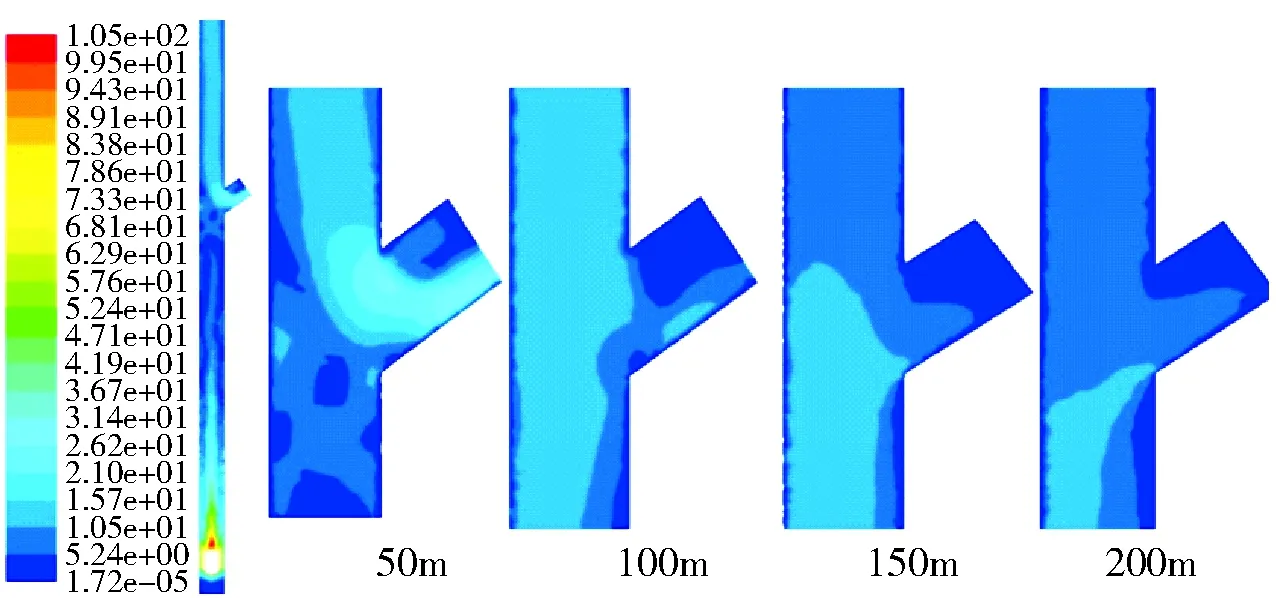
图13 z=0时刻各溜井口速度云图(6.9s)
通过对以上溜井放矿各时刻溜井内冲击气流产生的变化规律的研究,溜井内部气流流场可分涌入气流、反向气流、涡流、冲击气流等4个区域,其中涌入气流区域主要为放矿体后端溜井中心轴线至上部溜井口;反向气流区域主要为放矿体四周与溜井壁之间空隙;涡流区域为放矿体尾端近壁面和支岔溜井口拐角处内侧等区域;冲击气流区域为放矿体前端至下部溜井口。
3.2.3 各时间点溜井口风流分析
为了研究在溜井放矿过程中,各个溜井口产生的气流随时间的变化,在用FLUENT 进行模拟的过程中对每个溜井口设置了速度监控,并分别提取1、2.6、4、5、5.9s和6.5s等6个相对具有代表性的时间点的数据,如表1。
从表1和图14可以看到,在溜井放矿过程中,不同高度的支岔溜井口冲击风流与时间的关系,从图14中可以看出随着放矿体下落,各支岔溜井口依次产生最大的冲击气流,并且随着放矿高度的增大而增加。+200m标高溜井口在2.6s后冲击气流达到最大,此后该溜井口气流均以从井口外向溜井内涌入的气流为主,+150m标高支岔溜井口在4s后达到最大的冲击气流,此后该溜井口也产生涌入气流,+100m标高支岔溜井冲击气流达到最大约在5s之后,此时冲击气流大小达到约23m/s,在6s时,+100m标高支岔溜井口产生涌入气流,+50m标高溜井口冲击气流达到最大,风速约为34m/s,此处也是整个溜井中达到的最大冲击气流。当放矿体下落至+50m标高以下,溜井内产生反向气流,溜井内压力变大,+50m标高和+100m标高溜井口均受反向气流影响,+100m标高溜井口产生约1.5m/s的冲击气流,+50m标高溜井口产生约22m/s的冲击气流,较5s时有所下降。6.9s时溜井内气压增大,+100m标高溜井口冲击气流受其影响更加明显,冲击气流达到4.5m/s,+50m标高溜井口冲击气流速度变化不大,溜井上部支岔溜井口涌入气流速度基本稳定在4m/s。
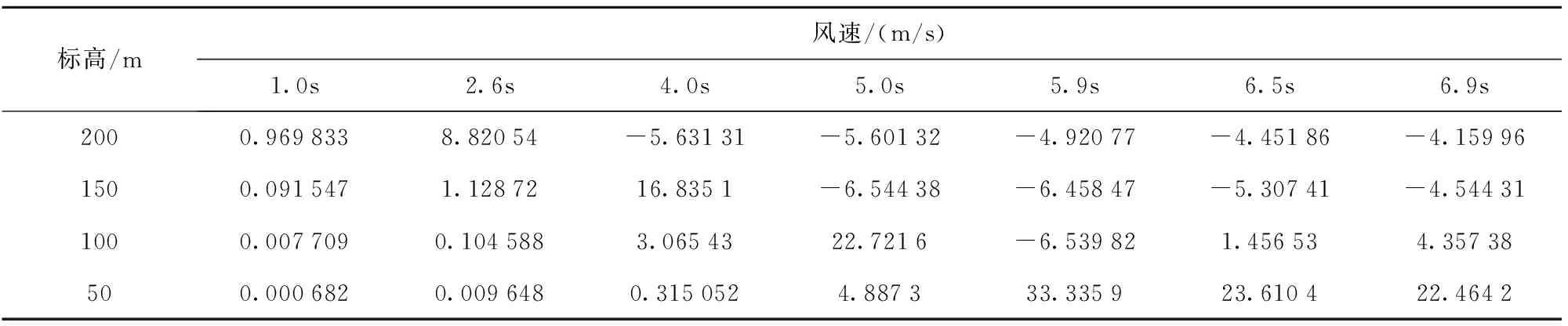
表1 溜井口风流风速表
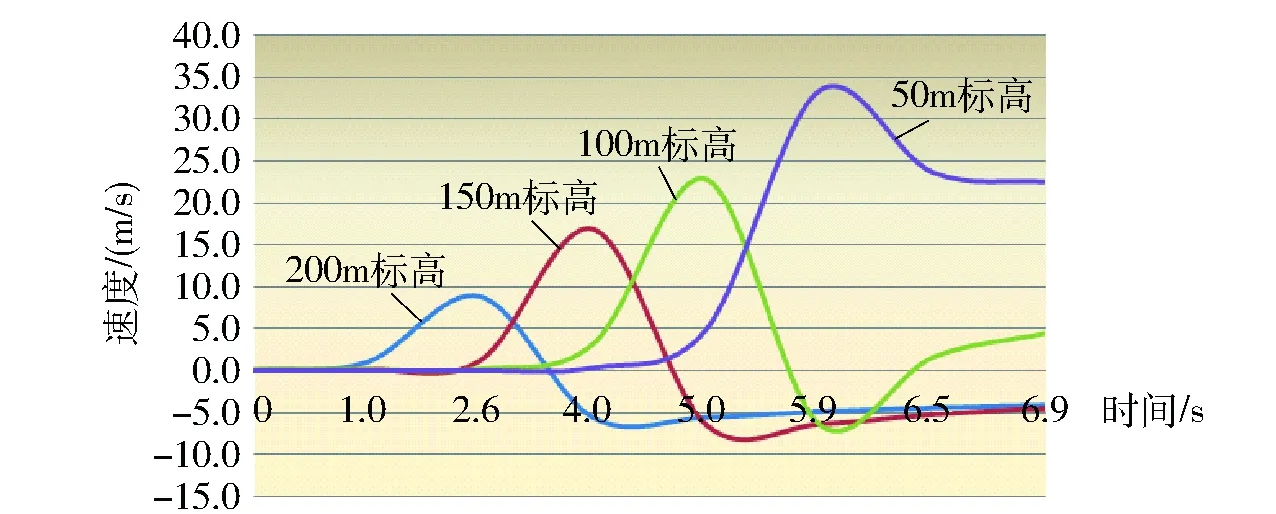
图14 各溜井口风流风速曲线图
4 结论
通过理论与模拟相结合的方法对溜井卸矿时冲击气流进行了分析研究,得出了以下结论。
(1)溜井放矿过程中,随着放矿体下落、速度的增加,放矿体前端正压和后端负压力值不断增加,并且影响范围越来越大,放矿体前后的压力差愈来愈大,因此溜井内的活塞效应愈加明显。
(2)当放矿体下落到一定深度时,由于其下部没有出口,气流则从放矿体侧面冲出形成反向气流,放矿体下方的溜井内正压力在短时间内急剧增加,可达到3~4kPa,且几乎分布于整个下部溜井内。
(3)溜井内部气流流场可分为涌入气流区域、反向气流区域、涡流区域、冲击气流区域4个区域,其中涌入气流区域主要为放矿体后端溜井中心轴线
至上部溜井口;反向气流区域主要为放矿体四周与溜井壁之间空隙;涡流区域为放矿体尾端近壁面和支岔溜井口拐角处内侧等区域;冲击气流区域为放矿体前端至下部溜井口。
(4)随着放矿体下落,各支岔溜井口依次产生最大的冲击气流,并且随着放矿高度的增大而增加。
[1] 高文远,徐忠光.大断面长溜井高位堵塞疏通处理实践研究[J].金属矿山,2009,(10):39-41.
[2] 张 蕊.深部开采·亟待解决的矿山开采现状(2011年全国金属矿山现代采矿关键技术学术研讨会)[J].矿业装备,2011,Z2(11):72-73.
[3] 郭延辉,侯克鹏,等.地下金属矿山深部开采引起地表移动变形规律研究[J].有色金属(矿山部分), 2011,63(5):36-40.
[4] 陈国军.分段瀑布式溜井系统在白音诺尔铅锌矿中的实践应用[J].科技信息,2014,(6):206-207.
[5] 罗 曼.用沙坝矿高大副井改主溜井的研究[D].长沙:中南大学,2004.
[6] 王 韦,陈正林,魏 鸿.高速铁路隧道内列车活塞风和空气阻力的解析计算[J].世界隧道,1999,(1):63-66.
[7] 金学易.隧道通风与隧道空气动力学[M].北京:中国铁道出版社,1983.
[8] 田 峰,王海桥,黄俊歆.矿井立井提升设备活塞作业理论分析[J].黑龙江科技学院学报,2006,(3):163-166.
[9] 王海桥,田 峰,吴 强.装备提升容器的通风井筒非稳态活塞风研究[C].淮南:中国(淮南)煤矿瓦斯治理技术国际会议论文集,2007:497-502.
[10] 王海桥,田 峰,施式亮,吴 强.矿井井筒提升容器活塞风效应分析及计算[J].湖南科技大学学报(自然科学版),2007,22(3):14.
[11] 陈 亮,邬长福,姚贵佳,陈祖云.溜井卸矿冲击气流影响因素模拟分析[J].矿业研究与开发,2016,36(3):1-5.
Numerical simulation study on impact airflow field in chute drawing
In order to understand the basic law of impact air flow and control the dust pollution effectively in orepass, the impact air flow formed during chute unloading was analyzed based on hydrodynamics, and the relation of impact air flow and unloading height was deduced. The impact airflow field distribution, pressure field distribution and the changing rule of air flow with time at each chute mouth during chute unloading were simulated by using FLUENT software. The results showed that during chute drawing the front positive pressure and rear negative pressure of ore drawing increased, and the piston effect in chute was obvious. The airflow field in orepass can be divided into inrush area, reverse area, eddy current region and impact air flow area. With the downfall of ore the largest impact air flow formed at each diversion chute mouth in turn and it increased with the increasing of drawing height.
chute; impact air flow; flow field; numerical simulation
TD521+.1
A
2017-02-23
汤民波(1987-),男,河南南阳人,硕士,讲师,主要从事工业安全与卫生、矿业工程专业教学与科研工作。
1672-609X(2017)03-0057-06

