轮腿混合机器人机械腿动力学建模与驱动预估

曲梦可， 王洪波， 荣誉

(1.燕山大学 河北省并联机器人与机电系统实验室, 河北 秦皇岛 066004; 2.河北科技师范学院 城市建设学院, 河北 秦皇岛 066004;3.燕山大学 先进锻压成形技术与科学教育部重点实验室, 河北 秦皇岛 066004)

轮腿混合机器人机械腿动力学建模与驱动预估

曲梦可1,2,3， 王洪波1,3， 荣誉2

(1.燕山大学 河北省并联机器人与机电系统实验室, 河北 秦皇岛 066004; 2.河北科技师范学院 城市建设学院, 河北 秦皇岛 066004;3.燕山大学 先进锻压成形技术与科学教育部重点实验室, 河北 秦皇岛 066004)

提出了一种可以同时实现迈步行走、有动力轮式机动、无动力轮旱冰式滑行3种运动方式的轮腿混合四足军用机器人，它采用一种基于3-UPS机构的6自由度并联机械腿，对并联机械腿进行了动力学建模与驱动参数峰值预估。通过矢量回路法推导出机械腿的机构传递映射模型，并建立了机构的雅可比矩阵；采用非保守系统的拉格朗日方程建立了机械腿的动力学模型，得到了驱动参数与机械腿的运动函数之间的显式方程。通过机械腿的动力学模型，对6个伺服电机的驱动转速、力矩进行了峰值预估分析，计算出各伺服电机中的最大理论转速为19.7 r/s，最大理论力矩为71 mN·m. 通过一个具体的机械腿设计方案和结构参数算例，分析了机器人按照“1-2-3-4”循环步态迈步行走过程中，其6个伺服电机的瞬时转速、瞬时力矩随时间的变化规律曲线，并计算出此算例的伺服电机最大转速为15.3 r/s，最大力矩为48.1 mN·m，均小于预估模型中的预估理论极限峰值，通过计算得出算例的伺服电机选型预估功率为77 W，算例结果证明了所建立的驱动参数峰值预估模型的合理性。

机械学； 机器人； 轮腿混合； 并联机械腿； 动力学分析； 拉格朗日方程； 峰值预估模型

0 引言

能够自主移动的军用机器人是目前机器人领域的研究热点之一[1-2]。自主移动军用机器人主要采用履带式、轮式、足式结构[3-8]。其中：履带式机器人属于传统越障结构[9]；轮式机器人采用类似车辆的方式移动[10]，这种方式在严重崎岖路面和废墟的适应性较差；足式机器人能够以迈步方式通过崎岖路面或废墟等地域[11]，但其在远距离平整路面机动时能耗较高、效率较低。轮腿混合式军用机器人是一种兼具轮式移动和迈步行走功能的机器人，在未受损公路和平坦地面通过轮式移动，在崎岖山地和灾害损毁区域通过足式迈步行走，在执行具体军用任务过程中可以根据路况随时转换移动方式[12-13]。常见的轮腿混合式机器人构型包括： 用于星际探索的Rolling-Wolf构型机器人[14-15]；机械腿末端装有动力驱动轮的ATHLETE类机器人[16-17]；机械腿末端加装无动力的轮子，以旱冰方式滑行前进的机器人[18-19]。如果一个机器人可以在有动力轮式机动、无动力轮式旱冰滑行和足式迈步机动之间转换，将使其具有超强的环境通过能力。并联机构的承载能力强、结构紧凑、运动链短、运动精度高，十分适合作为轮腿混合机器人的机械腿结构。已有的针对并联结构机械腿的研究主要有：上海交通大学高峰团队的四足、六足系列机器人[20-27]；燕山大学王洪波团队的四足、两足可重组机器人[28]等。

对机构进行动力学研究可以获得机器人的动态特性与函数模型，在设计阶段可以为机器人的驱动器参数选型提供依据，在试验阶段可以为机器人的控制建模提供基础。较为常见的机器人动力学分析方法主要有Lagrange法[29]、Newton-Euler法[30]、虚功原理法[31]、Kane方法[32]等，探索一种适用于轮腿混合机器人的机械腿动力学研究方法具有重要意义，可以有针对性地对其机械腿进行驱动参数预估和控制函数建模。

本文提出一种轮腿混合四足军用机器人和一种基于3-UPS机构的6自由度并联机械腿，其可以同时实现迈步行走、有动力轮式机动、无动力轮旱冰式滑行3种运动方式。在此基础上，采用非保守系统的拉格朗日方程对机械腿进行动力学建模；采用一种确定的机器人步态，对机械腿的伺服电机进行了转速、力矩峰值预估，计算出伺服电机的驱动参数峰值；以一组具体结构参数为实例，通过计算实例的驱动参数验证了动力学模型和驱动参数预估峰值的正确性。

1 机器人及并联机械腿构型

用于军事的轮腿混合四足机器人，如图1(a)所示，其整体结构由躯干和4条结构相同的6自由度并联机械腿及带有驱动轮的足组成。机器人可以实现3种运动方式：第1种，通过每个轮足上的驱动电机实现有动力的轮式机动，如图1(a)所示，此时每条机械腿的6自由度伺服运动主要用于对轮调姿以适应崎岖路面；第2种，将每条腿的轮置于水平让轮侧面着地，如图1(b)所示，此时每个轮侧面成为足的脚掌，机器人通过迈步方式机动；第3种，通过每条机械腿的6自由度伺服运动，使4个轮在无动力状态实现旱冰式滑行机动。

轮腿混合四足机器人的机械腿是一种基于3-UPS机构的6自由度并联机械腿，这里，U、P、S分别代表万向副、移动副和球面副，如图2所示。机械腿的3-UPS机构由固定平台、运动平台和二者之间的3条相同的UPS支链构成。其中，每条UPS支链的一端通过万向副与机构的固定平台连接，另一端通过球面副与机构的运动平台连接，在每条分支的万向副和球面副之间是一个由伸缩套筒构成的移动副。3条支链与机构固定平台连接的3个万向副回转中心点呈等腰直角三角形布局， 3条支链与运动平台连接的3个球面副回转中心点也呈等腰直角三角形布局。根据螺旋理论[33]，通过采用此种等腰直角三角形布局，可以实现机械腿足的3个转动运动之间解耦，同时使足的3个移动运动之间仅存在弱耦合，从而使机械腿的传递方程成为解耦传递方程，实现各驱动运动副之间输入力/力矩的解耦，提高机械腿的运动灵活性。

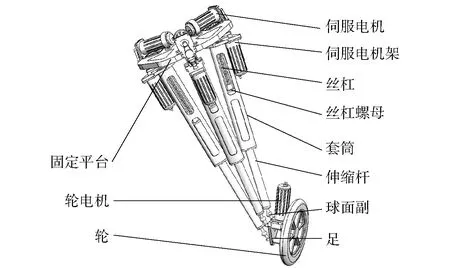
图2 机械腿结构图Fig.2 Structure of mechanical leg

采用约束螺旋法对机构进行自由度分析可知[33]，该机构每个支链均具有6个线性无关的自由度，所以其运动平台具有6个线性无关的自由度。为了实现对运动平台的6自由度伺服驱动，需要在每个支链选择2个驱动运动副，将3个支链的移动副选为移动驱动运动副，将3个支链万向副靠近固定平台的转动副选为转动驱动运动副，伺服电机的布置形式如图2所示。

2 机械腿的机构运动学分析

2.1 坐标系定义及姿态描述

机械腿的3-UPS机构如图3所示，采用矢量链进行构型描述和坐标系定义。定义运动平台的初始位姿为：运动平台与固定平台平行，且二者之间距离位于总变化范围的中间值h. 为了便于分析，本文根据前期对机械腿的运动学与构型设计的研究成果，确定初选结构参数：a=230 mm，b=70 mm，li∈(550 mm,950 mm)(i=1,2,3)，h=750 mm.

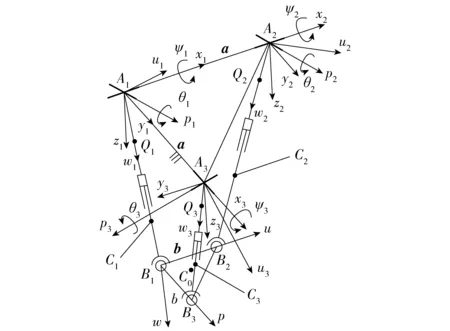
图3 机械腿3-UPS机构简图Fig.3 Sketch map of mechanical leg 3-UPS mechanism

在图3中，支链i(i=1,2,3)对应的下角标为i，Ai(i=1,2,3)是各支链与固定平台连接万向副回转中心点，Bi(i=1,2,3)是各支链与运动平台连接球面副回转中心点，A1和B1位于等腰直角三角形的直角顶点处。定义固定平台的结构参数A1A2=A1A3=a，运动平台的结构参数B1B2=B1B3=b，各支链的长度AiBi=li(i=1,2,3)。Qi(i=1,2,3)是各支链的移动副摆动套筒结构件的质心，Ci(i=1,2,3)是各支链的移动副伸缩杆质心，C0是运动平台质心。以A1为原点建立机构固定参考坐标系A1x1y1z1，其中：x1轴与位于A1点的万向副靠近固定平台的回转轴线重合；z1轴与点A1、A2、A3所张成的平面垂直，方向如图3所示；y1轴满足右手定则。又以Ai(i=2,3)为原点建立辅助参考坐标系Aixiyizi(i=2,3)，其中：xi轴与对应支链万向副靠近固定平台的回转轴线重合；zi轴与z1轴平行；yi轴满足右手定则。以B1为原点建立运动坐标系B1upw，其中：w轴与点B1、B2、B3所张成的平面垂直，方向如图3所示；u轴沿B1B2方向；p轴满足右手定则。为了描述各支链的姿态，在各支链上分别建立连体坐标系Aiuipiwi(i=1,2,3)，其中：wi轴与支链i的轴线重合并由点Ai指向点Bi；pi轴与对应支链万向副远离固定平台的回转轴线重合，方向如图3所示；ui轴满足右手定则。根据坐标系定义，连体坐标系Aiuipiwi(i=1,2,3)相对于参考坐标系Aixiyizi(i=1,2,3)的姿态可以通过两次旋转实现：首先绕xi轴旋转角度ψi，然后绕pi轴旋转角度θi.

基于图3中坐标系的定义，可以构造出连体坐标系Aiuipiwi(i=1,2,3)的旋转矩阵为

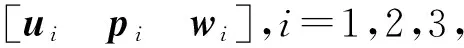
(1)

式中：ui、pi和wi分别为ui轴、pi轴和wi轴在固定坐标系A1x1y1z1中的单位主矢量。

经分析可知，ψi(i=1,2,3)即为各支链的转动驱动输入转角值。在选取运动平台参考点时，由于A1B1支链处于机构的对称面上，所以选取点B1为运动平台参考点。考虑到运动平台在固定参考坐标系A1x1y1z1中的姿态描述等效于先绕x1轴转γ角，再绕y1轴转β角，然后绕z1轴转α角获得，则运动坐标系B1upw相对于固定坐标系A1x1y1z1的旋转变换矩阵为

(2)

式中：u、p和w分别为u轴、p轴和w轴在固定坐标系A1x1y1z1中的单位主矢量。

2.2 雅可比矩阵求解

为了保证方程物理意义清晰，本文采用闭环矢量链的方法推导雅可比矩阵。在固定坐标系A1x1y1z1中，建立位置闭环矢量约束方程

l1=l1w1,

(3)

l1=ai+liwi-bi，i=2,3,

(4)

式中：li和wi(i=1,2,3)分别表示支链i的杆长和单位矢量；a2表示矢量A1A2；a3表示矢量A1A3；b2表示矢量B1B2；b3表示矢量B1B3.

通过求解(3)式、(4)式关于时间t的导数，可得

(5)

(6)

(7)

用矢量表达式(7)式可得

(8)

根据角速度叠加原理，可得

(9)

式中：ωi表示支链i(i=1,2,3)整体的角速度；xi和pi分别表示xi轴和pi轴在固定坐标系A1x1y1z1中的单位主矢量。

根据向量几何学可知，pi×pi=0，i=1,2,3. 因此，对(9)式两边同时叉乘pi(i=1,2,3)，对(5)式两端同时点乘p1，对(6)式两端同时点乘pi(i=2,3)，然后，将pi×ωi，i=1,2,3分别代入，可得

(10)

(11)

(12)

用矢量表达式(12)式可得

(13)

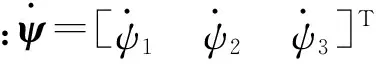
整理(8)式、(13)式就可以得到3-UPS机构的速度映射关系

(14)

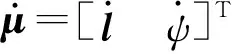
2.3 支链角速度分析

(15)

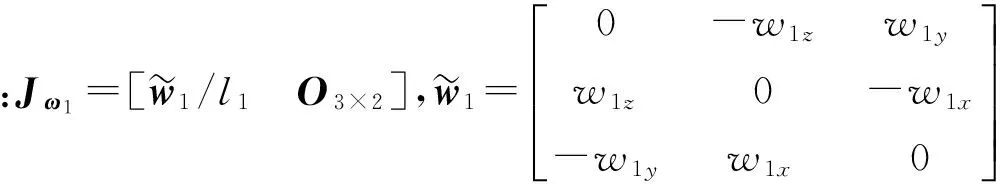
(16)

2.4 各构件质心位置、速度分析

机械腿的机构每个支链移动副摆动套筒仅绕其与固定平台连接的万向副回转中心点摆动，通过其支链的角速度可以求出其质心速度为

vqi=lqiwiωi，i=1,2,3,

(17)

式中：lqi是点Ai至点Qi的距离。

机构的各支链移动副伸缩杆质心Ci(i=1,2,3)在固定坐标系A1x1y1z1中的位置矢量pCi为

pC1=(l1-lC1)w1，

(18)

pCi=ai+(li-lCi)wi，i=2,3，

(19)

式中：lCi(i=1,2,3)是点Bi至点Ci的距离。

将(16)式等号两边同时求关于时间的导数，可得

(20)

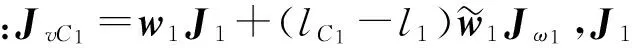
将(17)式等号两边同时求关于时间的导数，可得

(21)

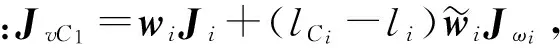
机械腿的机构运动平台质心点C0在运动坐标系B1upw中的位置矢量描述为pC0，运动平台质心点的速度为

(22)

3 机械腿的机构动力学建模

因为本文提出的轮腿混合军用机器人及其机械腿材质采用金属材料制作主要构件，其运动副及构件的弹性变形相对较小，且机器人的工作环境中地面粗糙，弹性变形相对于机器人运动环境的外部粗糙度可以忽略，所以，可以将机械腿简化为刚体进行动力学分析。为了便于动力学建模，这里首先对机械腿的机构进行分析条件假设：根据体积与质量比，各支链的万向副零部件体积和质量相对于机械腿而言非常小，所以在建模时将万向副零部件的转动惯量忽略；因为各支链的构件均采用回转体结构，所以其在各自局部连体坐标系中的惯量矩阵均为对角矩阵；因为3个转动驱动运动副的伺服电机转子相对于机械腿整体而言转速较小，所以将其转动惯量忽略。

3.1 广义力

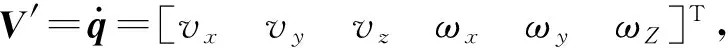
(23)

F=(J′)Tτ.

(24)

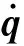
(25)

式中：Jω0=[O3×3E3×3]，O3×3为3阶0矩阵，E3×3为3阶单位矩阵。

3.2 部件动能和势能建模

机械腿的机构各种部件可以按照4类进行动能建模：第1类，各支链驱动移动副伸缩杆；第2类，各支链驱动移动副摆动套筒组件；第3类，各支链驱动移动副伺服电机转子和丝杠总成；第4类，机械腿的运动平台。

各支链移动副伸缩杆在固定坐标系A1x1y1z1中的动能描述为

(26)

式中：mCi是伸缩杆i的质量；ICi是伸缩杆i绕其质心垂直轴的惯量矩阵；vCi和ωi分别是伸缩杆i的质心速度和整体角速度。

各支链移动副摆动套筒在固定坐标系A1x1y1z1中的动能描述为

(27)

式中：IAi是摆动套筒绕其连接的万向副回转中心轴的惯量矩阵；ωi是摆动套筒i的整体角速度。

各支链驱动移动副伺服电机转子和丝杠总成在固定坐标系A1x1y1z1中的动能描述为

(28)

式中：ISAi是丝杠和电机转子总成绕其连接的万向副回转中心轴的惯量矩阵；ωi是摆动套筒i绕万向副回转中心轴的角速度；ISi是丝杠和电机转子总成绕其自身轴线的惯量矩阵；ωSi是丝杠和电机转子总成绕其自身轴线的角速度。

机械腿的运动平台在固定坐标系A1x1y1z1中的动能描述为

(29)

式中：mC0是运动平台的质量；IC0是运动平台绕过其质心的垂直轴的惯量矩阵；vC0和ω′分别是运动平台的质心速度和整体角速度。

通过前面的建模，可以得到机械腿的机构系统的总动能为

(30)

将(26)式～(29)式代入(30)式，再将(15)式、(16)式、(20)式、(21)式、(22)式代入(30)式，可得

(31)

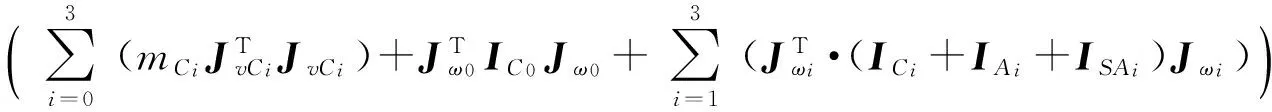
考虑到重力场的作用，机械腿的机构各部分势能建模相对容易，通过分析可得到系统的总势能为

(32)

式中：mqi和pqi分别是各支链移动副摆动套筒的质量和质心位置矢量；mCi和pCi分别是各支链移动副伸缩杆的质量和质心位置矢量；mSi和pSi分别是各支链丝杠和电机转子总成的质量和质心位置矢量；mC0和pC0是机构运动平台的质量和质心位置矢量。

3.3 机械腿的动力学方程

通过前文对机械腿的动能和势能建模，可以获得机械腿的系统拉格朗日函数为

L=T-V,

(33)

式中：T是系统的总动能；V是系统的总势能。

根据非保守系统的拉格朗日方程可知：

(34)

式中：qk(k=1,2,3,4,5,6)是机构的广义坐标；Fk(k=1,2,3,4,5,6)是与之对应的广义坐标的广义力。

将(33)式代入(34)式并以矢量形式表达，且因为势能V的函数中没有速度变量，可得

(35)

(36)

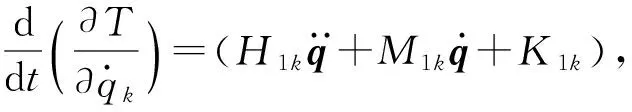
(37)

将(37)式整理成矢量表达，可得

(38)

式中：H1=[H11H12H13H14H15H16]T；M1=[M11M12M13M14M15M16]T；K1=[K11K12K13K14K15K16]T.

(39)

将(39)式整理成矢量表达，可得

(40)

式中：M2=[M21M22M23M24M25M26]T；K2=[K21K22K23K24K25K26]T.

(41)

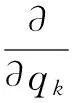
将(41)式整理成矢量表达，可得

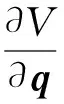
(42)

式中：Kg=[Kg1Kg2Kg3Kg4Kg5Kg6]T.

将(39)式、(40)式、(42)式代入(36)式，可得

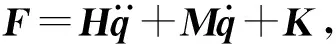
(43)式中，H是机构的实对称广义惯性矩阵;M是机构的离心力和哥氏力系数;K是机构的负载与重力项。

将(4)式代入(24)式，可得

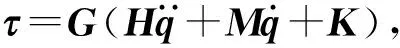
(44)

式中：τ=[τ1τ2τ3τ4τ5τ6]T是机构的驱动输入力矩矢量；G=(J′T)-1.

(44)式就是机械腿的机构逆动力学方程显式模型，通过给定机械腿的机构运动位置、速度、加速度等参数，利用(44)式便可以求出对应的各驱动运动副的驱动力/力矩，这些可以为机械腿的驱动参数预估提供依据。

4 机械腿的驱动参数峰值预估

本文提出的轮腿混合军用四足机器人可以同时实现迈步行走、有动力轮式移动、无动力轮旱冰式滑行3种运动方式。其中，迈步行走对机械腿的驱动速度与驱动力矩要求最高，当机器人以最大的速度各向迈步运动时，其机械腿的抬腿与迈步均可导致伺服电机出现峰值转速和力矩。由于机器人的4条机械腿的结构全部相同，且每条机械腿的迈步运动函数及动态特性也非常接近，这里只选择躯干的左前位置的机械腿进行驱动参数峰值预估，以此为依据对机械腿进行伺服电机选型。

这里，为了更全面考虑机械腿的工况，设定机器人按照“1-2-3-4”循环步态进行驱动参数峰值分析，即机器人迈步时采用1条腿迈步-2条腿迈步-3条腿迈步-4条腿迈步循环的方式进行前进，从而模拟四足动物的迈步规律。基于此种步态，当机器人向其躯干正前方以最大速度行走时，机械腿的最前端UPS支链(见图3中支链3)移动驱动副伺服电机会产生最大瞬时转速，机械腿的中间UPS支链(见图3中支链1)转动驱动副伺服电机会产生最大瞬时转速；当机器人向与其躯干垂直的正侧方以最大速度行走时，机械腿的中间UPS支链(见图3中支链1)移动驱动副伺服电机会产生最大瞬时转速，机械腿的最前端UPS支链(见图3中支链3)转动驱动副伺服电机会产生最大瞬时转速。在上述运动过程中，对应产生最大瞬时转速的伺服电机会产生峰值驱动力矩。设定分析的假设条件为：整个运动过程中地面保持水平；机械腿在迈步全过程足的姿态保持水平；机器人在运动过程中躯干保持水平。为了便于编程，设定在上述两种运动情况中，机械腿的运动平台(足)参考点B1在空间运动轨迹为余弦曲线，其轨迹函数为vx1(t)、vy1(t).

4.1 伺服电机驱动速度峰值分析

根据机械腿的机构速度传递模型，将(14)式中的速度雅可比矩阵以向量形式表达，可得

(45)

式中：Ji是支链i(i=1,2,3)的移动/转动驱动速度子向量，且Jli∈R1×6、Jψi∈R1×6.

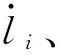
(46)

将(45)式代入(46)式，可以建立各驱动伺服电机的转速与运动平台(足)参考点B1的广义速度矢量之间关系：

(47)

将轨迹函数vx1(t)、vy1(t)代入(47)式就可以获得各驱动伺服电机的转速函数为

(48)

为了量化(48)式中的各函数，将轨迹函数具体化为

(49)

经分析可知，机器人向其躯干正前方以最大速度行走时产生的伺服电机转速大于其向与其躯干垂直的正侧方以最大速度行走时对应值，因为其向正前方行走时迈步的幅度更大。基于上述计算结果，如果机械腿的伺服电机全部采用相同的型号，那么伺服电机选型的最大理论转速为19.7 r/s.

4.2 伺服电机驱动力矩峰值分析

通过定义驱动力矩传递系数λli、λψi(i=1,2,3),建立各伺服电机驱动力矩εli、εψi与各驱动运动副的驱动力/驱动力矩τli、τψi(i=1,2,3,4,5,6)之间的传递关系

(50)

因为伺服电机峰值驱动力矩一般出现在高速启动、减速、急停等状态，所以，可以将(44)式中的离心力和哥氏力系数项忽略，并将(50)式代入(44)式，从而得到机构的显式加速度传递方程为

(51)

根据文献[20]可知，基于前文动力学模型建立的伺服电机驱动力矩峰值预估方程为

(52)

通过(52)式可以获得机构3个移动驱动副伺服电机的最大驱动力矩分别为εl1max=51 mN·m,εl2max=57 mN·m,εl3max=63 mN·m；3个转动驱动副伺服电机的最大驱动力矩分别为εψ1max=71 mN·m,εψ2max=47 mN·m,εψ3max=41 mN·m. 经分析可知，机器人向其躯干正前方以最大速度行走时产生的伺服电机力矩大于其向与其躯干垂直的正侧方以最大速度行走时对应值，因为其向正前方行走时迈步的幅度更大。基于上述计算结果，如果机械腿的伺服电机全部采用相同的型号，那么伺服电机选型的最大理论力矩为71 mN·m.

4.3 算例分析

为了验证前文驱动参数峰值预估模型的合理性，选择一组具体结构参数作为算例，如表1所示，进行驱动参数预估模型的验证。

表1 并联机械腿样机结构参数

在表1中，移动副套筒和伸缩杆的材料采用均质铝合金(密度2.88 kg/m3)，滚珠丝杠的材料采用均质轴承钢(密度7.81 kg/m3)，其余部件的材料采用40Cr钢(密度7.8 kg/m3)。各部件的惯量矩阵可以通过动力学分析软件Adams算出。因为机器人向其躯干正前方行走时产生的转速与力矩均大于其向正侧方行走，所以这里只分析其向正前方即轨迹函数vx1(t)时的伺服电机转速情况。

通过Matlab对(56)式进行编程建模计算，可以计算出同一条机械腿的3个移动驱动运动副和3个转动驱动运动副的伺服电机转速绝对值并绘制出其随时间变化曲线，如图4所示。

图4 机械腿各支链驱动速度曲线Fig.4 Driving speed curves of mechanical leg

通过图4可知，本算例的伺服电机最大驱动转速值分别为：nl1max=14.1 r/s,nl2max=14.7 r/s,nl3max=15.3 r/s；nψ1max=11.7 r/s,nψ2max=6.9 r/s,nψ3max=7.9 r/s. 这些峰值均小于本文获得的对应理论最大转速，验证了本文转速峰值预估模型的合理性。

通过Matlab对(59)式进行编程建模计算，可以计算出同一条机械腿的3个移动驱动运动副和3个转动驱动运动副的伺服电机力矩绝对值并绘制出其随时间变化曲线，如图5所示。

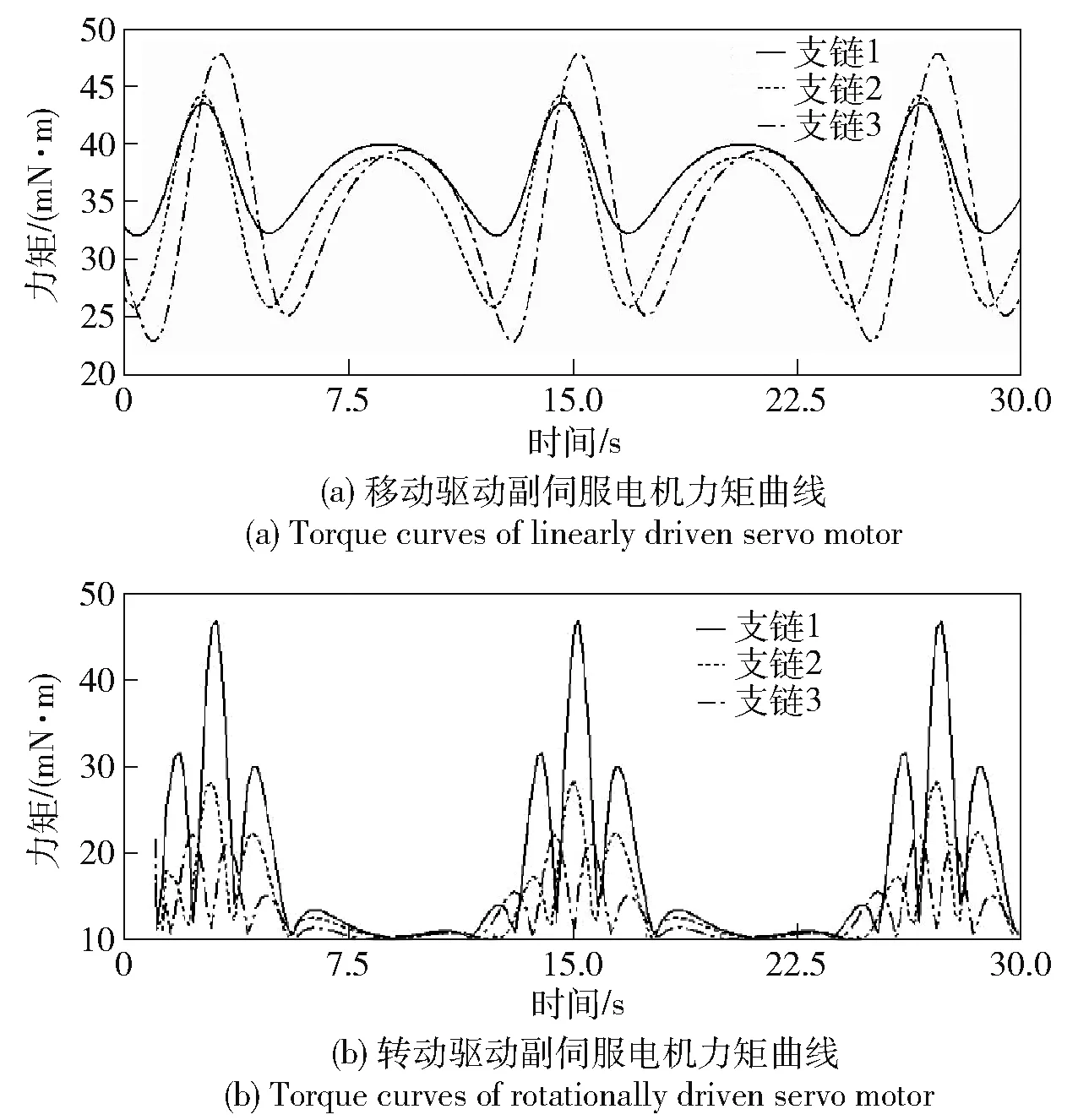
图5 机械腿各支链驱动力矩曲线Fig.5 Driving torque curves of mechanical leg

通过图5可知：本算例的3个移动驱动副伺服电机的最大驱动力矩分别为εl1max=43.7 mN·m,εl2max=44.1 mN·m,εl3max=48.1 mN·m；3个转动驱动副伺服电机的最大驱动力矩分别为εψ1max=46.7 mN·m,εψ2max=31.8 mN·m,εψ3max=27.7 mN·m. 这些峰值均小于本文获得的对应理论最大力矩，验证了本文力矩峰值预估模型的合理性。

通过前文对本算例的分析，根据直流伺服电机功率计算规律，在考虑功率损耗和机械效率的基础上，可以计算出本算例伺服电机选型的预估功率为77 W.

5 结论

1)提出了一种轮腿混合四足军用机器人及其6自由度并联机械腿，采用非保守系统的拉格朗日方程建立了机械腿的动力学模型，并推导出驱动参数与机械腿的运动函数之间的显式方程，获得了方程中各项系数的物理意义。

2)通过机械腿的动力学模型，建立了6个伺服电机驱动转速、力矩峰值预估模型，计算出各伺服电机中最大理论转速为19.7 r/s，最大理论力矩为71 mN·m.

3)通过一个具体的机械腿设计方案算例，分析了在机器人迈步行走过程中，其6个伺服电机的瞬时转速、瞬时力矩随时间的变化规律曲线，并计算出此算例的最大理论转速为14.7 r/s，最大理论力矩为48.1 mN·m，伺服电机选型的预估功率为77 W，算例结果证明了本文建立的驱动参数峰值预估模型的合理性。

References)

[1] 高峰, 郭为忠. 中国机器人的发展战略思考[J]. 机械工程学报, 2016, 52(7): 1-5. GAO Feng, GUO Wei-zhong. Thinking of the development strategy of robots in China[J]. Journal of Mechanical Engineering, 2016, 52(7): 1-6. (in Chinese)

[2] 田源木, 苏波, 许威. 四足机器人行走决策研究初探[J]. 兵工学报, 2014, 35(增刊1): 57-61. TIAN Yuan-mu，SU Bo，XU Wei. Preliminary research on walking decision of quadruped robot [J]. Acta Armamentarii, 2014, 35(S1): 57-61. (in Chinese)

[3] Estier T, Crausaz Y, Jacques B,et al. An innovative space rover with extended climbing abilities[C]∥Proceedings of IEEE International Conference on Robotics and Automation.San Francisco, CA, US: IEEE, 2000: 333-339.

[4] Eendo G, Hiros S. Study on roller-walker (multimode steering control and self-contained locomotion)[C]∥Proceedings of IEEE International Conference on Robotics and Automation. San Francisco, CA, US: IEEE, 2000: 2808-2814.

[5] Nakajima S, Nakano E. Adaptive gait for large rough terrain of a leg-wheel robot (fourth report: step-over gait)[J]. Journal of Robotics and Mechatronics, 2009, 21(2): 7-12.

[6] 陈勇, 王昌明, 包建东. 新型爬壁机器人磁吸附单元优化设计[J]. 兵工学报, 2012, 33(12): 1539-1544. CHEN Yong, WANG Chang-ming, BAO Jian-dong. Optimization of a novel magnetic adsorption unit for wall-climbing robot[J]. Acta Armamentarii, 2012, 33(12): 1539-1544.(in Chinese)

[7] 李研彪, 李景敏, 计时鸣，等. 一种3自由度并联拟人机械腿的动力学建模及伺服电机峰值力矩预估[J]. 兵工学报, 2014, 35(11): 1929-1936. LI Yan-biao, LI Jing-min, JI Shi-ming, et al. Dynamic modeling and peak torque prediction of servo motor for a 3-DOF parallel humanoid mechanical leg[J]. Acta Armamentarii, 2014, 35(11): 1929-1936. (in Chinese)

[8] 荣誉, 金振林, 崔冰艳. 六足农业机器人并联腿构型分析与结构参数设计[J]. 农业工程学报, 2012, 28(15): 9-14. RONG Yu, JIN Zhen-lin, CUI Bing-yan. Configuration analysis and structure parameter design of six-leg agricultural robot with parallel-leg mechanisms[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(15): 9-14. (in Chinese)

[9] 张豫南, 黄涛, 张舒阳，等. 一种履带式全方位移动平台转向滑移功率比分析[J]. 兵工学报, 2015, 36(8): 1562-1568. ZHANG Yu-nan, HUANG Tao, ZHANG Shu-yang,et al. Analysis about steering slip power ratio of a tracked omnidirectional mobile platform[J]. Acta Armamentarii, 2015, 36(8): 1562-1568. (in Chinese)

[10] 孙扬, 陈慧岩. 无人地面车辆测评体系研究[J]. 兵工学报, 2015, 36(6): 978-986. SUN Yang, CHEN Hui-yan. Research on test and evaluation of unmanned ground vehicles[J]. Acta Armamentarii, 2015, 36(6): 978-986. (in Chinese)

[11] 张金柱, 金振林, 陈广广. 六足步行机器人腿部机构运动学分析[J]. 农业工程学报, 2016, 32(9): 45-52. ZHANG Jin-zhu, JIN Zhen-lin, CHEN Guang-guang. Kinematic analysis of leg mechanism of six-legged walking robot [J]. Transactions of the Chinese Society of Agricultural Engineering, 2016, 32(9): 45-52. (in Chinese)

[12] 刘呈则, 严智, 邓景珊，等. 核电站应急机器人研究现状与关键技术分析[J]. 核科学与工程, 2013, 33(1): 98-105. LIU Cheng-ze, YAN Zhi, DENG Jing-shan,et al. Study on accident response robot for nuclear power plant and analysis of key technologies[J]. Nuclear Science and Engineering, 2013, 33(1): 98-105. (in Chinese)

[13] 刘波, 王欣, 吴王锁，等. 机器人在核与辐射事故应急中的应用展望[J]. 工业安全与环保, 2015, 41(1): 62-64. LIU Bo, WANG Xin, WU Wang-suo,et al. The application prospect of robot in the nuclear and radiation emergency [J]. Industrial Safety and Environmental Protection, 2015, 41(1): 62-64. (in Chinese)

[14] Volpe R, Balaram J, Ohm T,et al. Rocky 7: a next generation mars rover prototype[J]. Advanced Robotics, 1997, 11(4): 341-358.

[15] Kemurdjian A L.Planet rover as an object of the engineering design work[C]∥Proceedings of the 1998 IEEE International Conference on Robotics & Automation. Leuven , Belgium: IEEE,1998: 140-145.

[16] COLLINS C. Stiffness modeling and force distribution for the all-terrain hex-limbed extra-terrestrial explorer (ATHLETE) [C]∥2007 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference. Las Vegas, NV,US: ASME, 2007: 1-9.

[17] Smith J A, Sharf I, Trintini M T. PAW: a hybrid wheeled-leg robot[C]∥Proceedings of International Conference on Robotics and Automation. Orlando, FL, US: IEEE, 2006: 4043-4048.

[18] Wang P F, Huang B, Sun L N. Walking research on multi-motion mode quadruped bionic robot based on moving ZMP[C]∥Proceedings of IEEE International Conference on Mechatronics & Automation. Toronto, Ontario, Canada: IEEE, 2005: 1935-1940.

[19] Endo G，Hirose S. Study on roller-walker -multi-mode steering control and self-contained locomotion)[C]∥Proceedings of the IEEE International Conferences on Robotics and Automation. San Francisco， CA，US: IEEE, 2000: 2808-2813.

[20] 潘阳. P_P结构六足机器人性能设计与控制试验研究[D]. 上海: 上海交通大学, 2014: 29-55. PAN Yang. Performance design and control experiment of a novel hexapod robot with P-P structure [D]. Shanghai: Shanghai Jiao Tong University, 2014: 29-55. (in Chinese)

[21] 荣誉. 基于并联机械腿的六足机器人分析与设计[D].秦皇岛: 燕山大学, 2015: 17-88. RONG Yu. Analysis and design for hexapod robots with parallel mechanical legs[D]. Qinhuangdao: Yanshan University, 2015: 17-88. (in Chinese)

[22] 荣誉, 金振林. 五自由度并联机械腿静力学性能评价与优化设计[J]. 光学精密工程, 2012, 20(6): 1233-1242. RONG Yu, JIN Zhen-lin. Statics performance evaluating and optimal design of 5-DOF parallel mechanical leg[J]. Optics and Precision Engineering, 2012, 20(6): 1233-1242. (in Chinese)

[23] 荣誉, 金振林, 曲梦可. 六足步行机器人的并联机械腿设计[J]. 光学精密工程, 2012, 20(7): 1532-1541. RONG Yu, JIN Zhen-lin,QU Meng-ke. The design of a parallel mechanical leg of the six-legged robot[J]. Optics and Precision Engineering, 2012, 20(7): 1532-1541. (in Chinese)

[24] 荣誉, 金振林. 3-DOF并联机械腿动力学建模与伺服电机峰值预估[J]. 光学精密工程, 2012, 20(9): 1974-1983. RONG Yu, JIN Zhen-lin. Dynamic modeling and peak prediction of servo motor for 3-DOF parallel mechanical leg[J]. Optics and Precision Engineering, 2012, 20(9): 1974-1983. (in Chinese)

[25] 荣誉, 金振林, 曲梦可. 三自由度并联机械腿静力学分析与优化[J]. 农业工程学报, 2012, 28(20): 41-49. RONG Yu, JIN Zhen-lin, QU Meng-ke. Statics analysis and optimal design of 3-DOF parallel mechanical leg[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(20): 41-49. (in Chinese)

[26] 田兴华, 高峰, 陈先宝, 等. 四足仿生机器人混联腿构型设计及比较[J]. 机械工程学报, 2013, 49(6): 81-88. TIAN Xing-hua, GAO Feng, CHEN Xian-bao, et al. Mechanism design and comparison for quadruped robot with parallel-serial leg[J]. Journal of Mechanical Engineering, 2013, 49(6): 81-88. (in Chinese)

[27] 荣誉, 刘双勇, 韩勇. 六足制孔机器人三自由度并联机械腿的误差模型及验证[J]. 农业工程学报, 2016, 32(18): 18-25. RONG Yu, LIU Shuang-yong, HAN Yong. Error model and verification of three degrees of freedom parallel mechanical leg on hexapod drilling robot[J]. Transactions of the Chinese Society of Agricultural Engineering, 2016, 32(18): 18-25. (in Chinese)

[28] 王洪波,齐政彦,胡正伟,等.并联腿机构在四足/两足可重组步行机器人中的应用[J].机械工程学报,2009,45(8): 24-30. WANG Hong-bo, QI Zheng-yan, HU Zheng-wei, et al. Application of parallel leg mechanisms in quadruped/biped reconfigurable walking robot[J]. Journal of Mechanical Engineering, 2009, 45(8): 24-30. (in Chinese)

[29] 王跃灵, 金振林, 李研彪. 球面3-RRR并联机构动力学建模与鲁棒- 自适应迭代学习控制[J].机械工程学报, 2010,46(1): 68-73. WANG Yue-ling, JIN Zhen-lin, LI Yan-biao. Dynamic modeling and robust-adaptive iterative learning control of 3-RRR spherical parallel mechanism [J]. Journal of Mechanical Engineering, 2010, 46(1): 68-73. (in Chinese)

[30] Samper R E. A three degree of freedom parallel manipulator with only translational degrees of freedom [D]. Maryland: The University of Maryland, 1997: 83-97.

[31] Tsai L W. Solving the inverse dynamics of a Stewart-Gough manipulator by the principle of virtual work [J]. ASME Journal of Mechanical Design, 2000,122(1): 3-9.

[32] Samak S M, Gupta K C. Parametric uncertainty on manipulators dynamics [J]. Mechanism and Machine Theory, 1998, 33(7): 945-956.

[33] 黄真, 赵永生, 赵铁石. 高等空间机构学[M]. 北京: 高等教育出版社, 2006:277-283. HUANG Zhen, ZHAO Yong-sheng, ZHAO Tie-shi. Advanced spatial mechanism [M]. Beijing: Higher Education Press, 2006: 277-283. (in Chinese)

[34] 王振发. 分析力学[M].北京:科学出版社, 2002: 46-47. WANG Zhen-fa. Analytical mechanics [M]. Beijing: Science Press, 2002: 46-47. (in Chinese)

Dynamic Modeling and Driving Parameter Prediction of Mechanical Leg of Wheel-leg Hybrid Robot

QU Meng-ke1,2,3， WANG Hong-bo1,3， RONG Yu2

(1.Parallel Robot and Mechatronic System Laboratory of Hebei Province, Yanshan University, Qinhuangdao 066004, Hebei, China; 2.College of Urban Construction, Hebei Normal University of Science and Technology, Qinhuangdao 066004, Hebei, China; 3.Key Laboratory of Advanced Forging & Stamping Technology and Science of Ministry of Education, Yanshan University, Qinhuangdao 066004, Hebei, China)

A new type of wheel-leg hybrid quadruped robot is proposed, which has four 6-DOF mechanical legs based on 3-UPS parallel mechanism. The dynamics of mechanical legs are modeled, and their driving parameters are predicted. The vector chain method is used to establish a transfer model of 3-UPS parallel mechanism, and the Jacobian matrix is established. A dynamics model of mechanical legs is established based on the Lagrange equation, and the drive force acted on the mechanism is given. The peak prediction model of servo motors for driving speed and torque is analyzed based on the dynamics model. The calculated result shows that the peak value of rotating speed of driving motor is 19.7 r/s, and the peak value of torque of driving motor is 71 mN·m. A design scheme of mechanical leg and its structure parameters are used to obtain the changes of driving speeds and torques of 6 motors over time. The calculated results show that the peak speed of driving motor is 15.3 r/s, and its peak torque is 48.1 mN·m, which are all less than the predicted limit values. The predicted peak power of servo motors is 77 (W). It proves that the dynamic analysis and the peak prediction model of driving parameters of the mechanical leg are very reasonable.

mechanics; robot; wheel-leg hybrid; parallel mechanical leg; dynamic analysis; Lagrange equation; peak prediction model

2016-12-22

国家科技支撑计划项目(2015BAI06B01)；河北省高等学校科学技术研究青年基金项目(QN2015185)；河北科技师范学院博士启动基金项目(2015YB004)

曲梦可(1981—)，女，讲师，博士研究生。E-mail: lixiangcg@126.com

王洪波(1956—)，男，教授，博士生导师。E-mail: hongbo_w@ysu.edu.cn

TP242.3

A

1000-1093(2017)08-1619-11

10.3969/j.issn.1000-1093.2017.08.021