一种锂离子电池荷电状态估计与功率预测方法

程 泽 孙幸勉 程思璐

(1.天津大学电气自动化与信息工程学院 天津 300072 2.天津大学微电子信息学院 天津 300072)

一种锂离子电池荷电状态估计与功率预测方法

程 泽1孙幸勉1程思璐2

(1.天津大学电气自动化与信息工程学院 天津 300072 2.天津大学微电子信息学院 天津 300072)

为了能够准确估计锂离子电池的荷电状态(SOC)，同时对电池实际可用的最大充、放电功率进行预测，在研究电池充、放电过程中的滞回现象的基础上，建立基于电压滞回特性的二阶RC等效电路模型。为了避免因噪声统计特性造成的误差，将H∞滤波算法应用到锂离子电池的SOC估计中，减少了估计过程中的模型误差和算法误差，提高了估计的鲁棒性。将电池电压、电流和SOC的估计值作为联合约束条件预测锂离子电池实际可用的最大充、放电功率，对电池做脉冲充、放电实验，实验分析表明，与混合脉冲功率特性(HPPC)测试方法相比，联合约束算法提高了预测电池功率的准确性。

锂离子电池 电池模型 荷电状态 功率状态

0 引言

锂离子电池作为20世纪90年代研发推出的新型储能元件，应用场合已十分广泛，如便携式电子设备、新能源汽车、储能电源、军事航空领域等[1]。近年来，电动汽车技术发展迅速，但电动汽车的电池管理系统(Battery Management System，BMS)技术还不成熟[2]。BMS需要准确实时地估测动力电池组的荷电状态(State of Charge，SOC)，保证SOC维持在合理的范围内，防止由于过充电或过放电对电池造成损伤[3]。而对功率状态(State of Power，SOP)的了解，则可让电池在最大限度进行能量交换时保证电池的寿命。

准确估计锂离子电池的SOC是一项困难的任务，因为随着循环次数的增加，电池会发生不可逆的老化现象[4]，此时对SOC估计将出现很大的偏差。目前，国内外学者提出了多种估计SOC的方法，主要分为两类：①不基于模型的方法，如安时积分法[5]和开路电压法[6]，该类方法的优点是简单易用，不需要复杂的电池建模，缺点是精度不高；②基于模型的算法，如神经网络法[7]、卡尔曼滤波算法[8，9]、滑模观测器法[10]、粒子滤波器法[11]等，该类方法估计精度高，收敛性好，但是对电池模型要求高，计算复杂。

在电池功率预测研究方面，常采用脉冲充、放电的测试方式。美国USABC (United States Advanced Battery Consortium)峰值功率测试方法是测试不同放电深度下，电池在2/3开路电压(Open Circuit Voltage，OCV)处持续放电30 s的能力。因为该方法有80%放电深度的限制，所以其测得的功率略小于实际值，且其测试结果为静态峰值功率，并非实际运行工况中的动态峰值功率[12]。日本的JEVS (Japan electric vehicle association)功率密度测试法分别以1C、2C、5C、10C的电流对设定SOC下的电池进行交替充电或放电，充电或放电时间分别为10 s，实验期间记录电池充电或放电电压。该方法找到了截止电压限制条件下动态工况时的最大充、放电电流，但是没有考虑高倍率电流工况下电池放电能力的变化[13]。我国电池测试规范中规定：电池峰值功率为每一阶段脉冲放电闭路后0.1 s时的电压与电流的乘积；电池平均功率为每一阶段脉冲放电能量与放电时间的商，但该方法没有表述电池10 s持续峰功率值输出的能力。国内外的电池功率测试规范均无法提供电池的实际峰值输出功率[14]。

目前，在电池峰值功率预测中最为广泛且简单的方法是复合脉冲法。复合脉冲法估计锂离子电池功率状态[15]是基于锂离子电池的内阻模型[16]，利用当前SOC下的开路电压以及内阻估计出电池的瞬时SOP值。复合脉冲法所用的模型简单，计算量小，但电动车辆在实际运行过程中，电流变化非常剧烈，使用该方法会导致较大的误差。并且该方法并没有考虑电池充、放电电流阈值与SOC限制，估计的峰值功率偏大。

本文提出多参数联合约束SOP估计，考虑电压、电流、SOC的共同限制，预测电池10 s的持续峰值功率输出能力。

1 SOP预测中的滞回模型

电池模型的精度对功率预测的精度有很大影响。目前常用的锂离子电池电路模型主要有电化学模型[17]、神经网络模型[18]及等效电路模型等[19]。电化学模型能够很好地描述电池的特性，但其模型结构比较复杂，实现困难，参数获取步骤繁琐；神经网络模型优点是估计精度较高，缺点是需要大量数据进行离线训练、耗时较长，并且估计精度受训练方法影响较大；等效电路模型将电池视为动态系统，通过对电池建模完成状态空间描述，再运用各种滤波器或观测器对状态量进行估计。

1.1 考虑滞回特性的电路建模

滞回特性是锂离子电池的基本特性之一，它是指电池在相同SOC下充电过程的开路电压与放电过程的开路电压不一致的现象。滞回现象产生的原因与电池内部的材料特性相关[20]，为了研究锂离子电池的滞回特性，有学者在等效电路模型的基础上引入了描述滞回特性的电路参数[21，22]，这种方法很大程度上提高了精度，但该方法使得模型参数明显增多，计算成本较大，不适合工程应用。为了兼顾模型的复杂度和可实现性，在分析滞回特性实验的基础上，力求建立考虑滞回特性的锂离子电池模型。

为了对电池的滞回特性研究和建模，进行了脉冲充、放电实验，分别测试了电池在完整SOC周期下和局部SOC周期下的OCV-SOC特性，即滞回主回路特性和滞回小回路特性。主回路SOC变化方向为0%→100%→0%，小回路SOC变化方向为100%→30%→70%→30%→100%，测试过程中电池的电压和电流变化曲线如图1、图2所示。对数据处理后，得到电池在室温条件下静置1 h的滞回特性曲线，如图3所示，图中黑色箭头表示SOC的变化方向。

图1 滞回主回路测试电压和电流曲线Fig.1 Voltage and current curves of hysteresis major loop

图2 滞回小回路测试电压和电流曲线Fig.2 Voltage and current curves of hysteresis minor loop

图3 滞回回路特性曲线Fig.3 Hysteresis loop characteristic curves

由图3可知，OCV-SOC曲线越接近于滞回主回路特性曲线，其逼近速度就越小，利用这个特点选取如下滞回模型，使得锂离子电池的开路电压在充、放电过程中逐渐趋向滞回主回路中的电压曲线，即通过调整OCV-SOC曲线斜率加快其趋向主回路曲线的速度，即

(1)

式中，UOCVc和UOCVd分别为主回路充电过程和放电过程的开路电压；UOCV为电池实际运行时的开路电压；η为调整系数，本文取η=10。式(1)离散化得

UOCVnew(k)=

(2)

式中，UOCVc(k)和UOCVd(k)分别为k时刻主回路充电过程和放电过程的开路电压；UOCVnew(k)为k时刻修正的开路电压；UOCV(k)为电池k时刻测量的开路电压；SOC(k)为k时刻的荷电状态。

为了验证上述模型的准确性，本文将实验得到的滞回小回路数据代入式(1)计算，结果如图4所示。滞回模型电压计算结果与充、放电循环测试电压误差如图5所示，最大误差为0.001 6 V，该模型输出值基本接近锂离子电池开路电压的真实值。将调整系数分段给定，可进一步提高模型精度。

图4 滞回特性模型估计曲线Fig.4 Estimated curves of hysteresis characteristics model

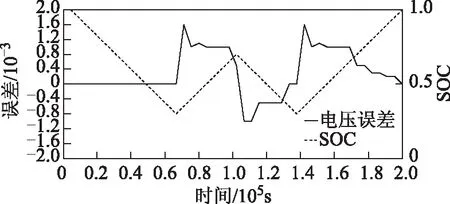
图5 滞回特性误差分析曲线Fig.5 Hysteresis characteristic curve

本文采用如图6所示的二阶RC滞回等效电路模型对电池特性进行研究。模型分为两部分，左边为基于滞回模型的滞回电压计算部分，其计算可很好地校正电池开路电压与SOC之间的关系；右边的二阶RC网络用来表示电池的静置特性，各部分的电压、电流关系为

(3)

式中，It为端电流；U0为R0两端电压；R1、C1和R2、C2用来描述电池的极化效应；U1和U2分别为R1、C1和R2、C2两端的电压。式(3)离散化可得

(4)

式中，τ1=R1C1；τ2=R2C2。

图6 二阶RC滞回等效电路模型Fig.6 Two order RC hysteresis equivalent circuit model

综合电路的两个部分和计算SOC的安时积分法，等效滞回模型为

(5)

式中，ηn为库伦效率，一般设充电效率ηn=1，放电效率ηn<1；T为采样周期；Qn为电池的额定容量。

本文采用最小二乘法动态辨识等效电路模型的各个参数值。基于脉冲放电数据的辨识结果如图7所示，可见锂离子电池的参数均会随着电池的充、放电过程变化，其中等效内阻在电池电量将尽时急剧增大。

图7 参数辨识曲线Fig.7 Parameters identification curves

1.2 模型的仿真与验证

本文在Matlab的Simulink中搭建了电池的等效滞回模型和二阶RC模型，并进行恒流脉冲仿真实验。同时在室温条件下对电池以C/3的电流进行恒流脉冲充、放电，再将电池端电压的测量值和模型的仿真值进行比较，结果如图8所示。可看出，使用二阶RC模型估计所得的电压，在电池低电量时误差较大，最大误差达到80 mV。这是由于电池在低电量时，内部化学成分发生变化，等效模型的参数必然不准确。而等效滞回模型的预测精度则高于二阶RC模型，可很好地跟踪电压真实值。

图8 脉冲放电实验下的模型验证结果及误差曲线Fig.8 The model validation results and error curves of pulse discharge experiments

2 基于H∞滤波算法的SOC估计

2.1 H∞滤波算法概述

扩展卡尔曼滤波(Extended Kalman Filter，EKF)在实际中应用十分广泛，但是其一些先天性缺陷导致其使用范围受限。只有预知系统噪声的统计特性，应用EKF滤波算法才能得到较好的估计结果，因此精度常常不能达到工程要求。如果不能预知系统的准确先验信息，则需要在设计卡尔曼滤波器时增大噪声协方差矩阵的取值，以增大对实时测量的利用权重，同时降低对一步预测的利用权重，该方法俗称调谐[23]。但是调谐存在一定盲目性，无法确定究竟增大到多少才能使估计精度达到最佳。并且，如果系统的测量噪声和过程噪声不是白噪声，或者存在偏差量时，则卡尔曼滤波效果会严重恶化，甚至发散[24]。以上缺陷使EKF的实际运用并不理想。

针对上述问题，本文采用H∞滤波算法来估计电池的SOC。H∞滤波算法只要求系统的噪声信号为能量有限的随机信号，并不要求预知精确的噪声统计特性，并且能在噪声干扰很大的情况下取得最小的估计误差[25]。H∞滤波算法设计思路是：在估计噪声、测量噪声和误差未知的情况下，将系统过程噪声、测量噪声和初始状态变量的不确定性对估计精度的影响降到最低，使滤波器在最恶劣的条件下估计误差达到最小。所以H∞滤波算法可看作是系统存在严重干扰情况下的最优滤波[26]。

2.2 基于H∞滤波的SOC估计方法

在使用H∞滤波算法时，假设电池状态空间表达式为

(6)

式中，xk为状态向量；yk为观测向量；zk为系统k时刻的估计输出向量；uk为k时刻系统的输入向量；Ak为系统状态转移矩阵；Bk为输入控制矩阵；Ck、Dk为观测矩阵；Γk为系统的干扰输入矩阵；Lk为系统的估计矩阵；wk、vk分别为系统的过程噪声和观测噪声。此处wk、vk均为预先不知道统计特性的有限能量噪声，即满足

(7)

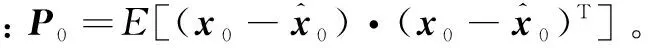
(8)

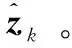
(9)

H∞最优滤波问题的解，可通过迭代H∞次滤波问题的γ来得到。由于电池模型的复杂的非线性的特点，因此在使用H∞滤波算法时，需要对非线性系统进行线性化处理。将其近似看作一个线性时变系统，再继续使用H∞滤波进行系统的状态估计。

(10)

其中

(11)

H∞滤波算法的递推方程为

(12)

(13)

(14)

(15)

式中，Kk+1为H∞滤波器增益。

可认为EKF是H∞滤波器的一个特例。当H∞滤波器中的γ∞时，Riccati递推方程就变成了卡尔曼滤波算法中的递推方程，但此时H∞滤波器算法的鲁棒性下降。而当γ为正整数时，虽然算法具有很好的鲁棒性，但可能无法取得最小的误差值。因此，在电动汽车动力电池的复杂工况下，H∞滤波算法具有更好的预测效果。

2.3 结果分析与验证

采用天津力神公司的LP2770102AC磷酸铁锂动力电池，通过电池在设定工况下充、放电实验验证H∞滤波算法在SOC估计方面的优越性。

对电池进行DST(dynamic stress test)电流工况充、放电，DST工况循环5次，每次循环都包含大电流的充电和放电过程，共14个步骤。图9为锂离子电池的实验端电压和电流。SOC的估计结果如图10、图11所示。

图9 DST工况下的实验端电压和电流Fig.9 Experiment terminal voltage and current in DST condition

图10 SOC比较曲线Fig.10 SOC comparison curves

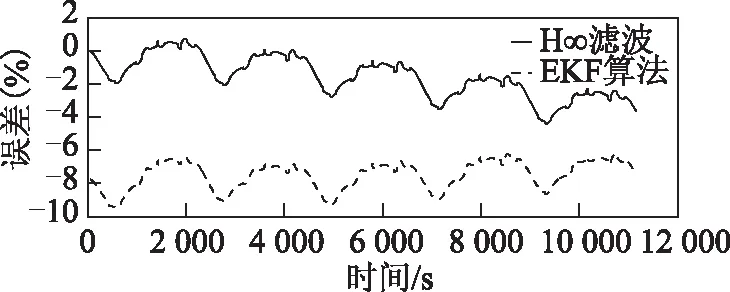
图11 DST工况SOC估计误差对比Fig.11 SOC estimation error comparison in DST condition

在DST工况下，电流变化非常剧烈。这种情况下，不仅电池模型的噪声很大且不再呈现白噪声的特点，而且电池模型参数也因电流的剧烈变化而发生较大的改变。此时若继续使用EKF算法，则电池模型的输出电压会更加偏离真实值，趋于发散状态。通过图11 可看出，H∞滤波算法和EKF算法的最大误差分别为5%和10%。

从上述实验结果和分析中可看出，在电池SOC估计方面，鲁棒H∞滤波算法是比EKF算法有优势的：①鲁棒H∞滤波算法的鲁棒性明显要强于EKF，不论系统噪声和测量噪声统计特性如何，都能保证滤波精度，受建模精度和环境因素的影响很小；②鲁棒H∞滤波算法比EKF算法适用范围更广且更灵活，可根据实际情况，通过随时调整γ的值达到更加满意的滤波效果。

3 基于滞回动态模型的多参数SOP估计

本文提出的功率预测方法将综合考虑电动汽车正常使用过程中SOC、电池截止电压对最大峰值功率的限制问题。

3.1 考虑SOC的约束估计最大充、放电电流

电池峰值功率的准确预测依赖于电池SOC估计值的精度。本文电池模型和SOC估计算法可在复杂工况下获得更好的估计结果。下面讨论SOC对功率状态的限。

假设时刻t时，以恒定电流it对电池进行放电或充电，则在Δt时间内，t+Δt时刻电池k的SOC可表示为

(16)

式中，SOCk(t)为电池k在t时刻的SOC值；SOCk(t+Δt)为t+Δt时刻的SOC值。假设电池正常工作时SOC的范围为SOCmin≤SOCk(t)≤SOCmax，则当电池以最大电流放电Δt后，SOC不小于SOCmin；当电池以相应的最大充电电流充电Δt后，SOC不大于SOCmax。此处电池放电电流为正，充电电流为负(最大充电电流在代数式中表示最小负值)。对于电池组中的每一个电池，考虑SOC因素的影响，电池的最大充、放电电流分别为

(17)

(18)

3.2 考虑电池电压约束估计的最大充、放电电流

用状态空间表示电池模型，SOC作为系统的一个状态变量。则系统可表示为

(19)

Ut(m)=UOCV(SOC(m))-U1(m)-U2(m)-R0It(m)

(20)

假设为N个采样周期时长，则Δt时间后的电池端电压为

v(m+N)=UOCV(SOC(m+N))-U1(m+N)-

U2(m+N)-R0It(m+N)

(21)

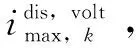
UOCV(SOC(m+N))-U1(m+N)-

U2(m+N)-R0It(m+N)-vmin=0

(22)

UOCV(SOC (m+N))-U1(m+N)-U2(m+N)-

R0It(m+N)-vmax=0

(23)

设状态方程中的状态变量为xk(t)，将xk(t)在m≤t≤m+N内线性化处理，得

xk(m+1)=Axk(m)+Bik(m)

(24)

式中，A和B为系数矩阵，且

在m≤t≤m+N时间内，电流保持恒定，则

(25)

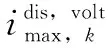
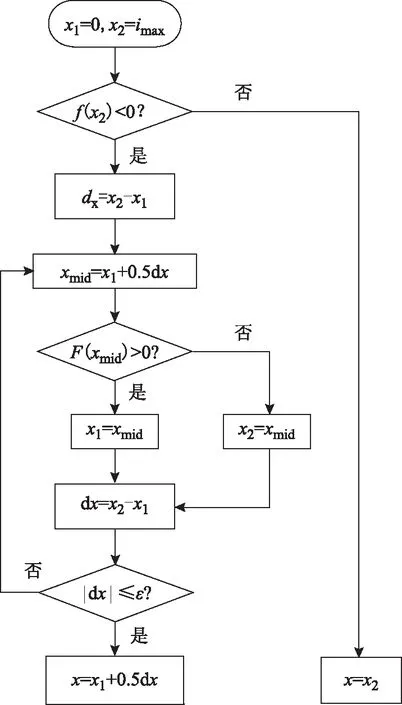
图12 二分查找算法流程Fig.12 Process of binary search algorithm

3.3 多参数约束法下的峰值功率计算

根据最大电流，得到电池组的峰值功率为

(26)

(27)

至此，基于电池滞回二阶模型，采用多参数联合约束的方法，完成了对电池最大充、放电功率的实时预测，并估计了电池的充、放电能力。

3.4 结果分析与验证

为了验证多参数联合约束算法预测峰值功率的准确性，对电池进行8 A的恒流脉冲放电实验和6.25 A的恒流脉冲充电实验。这种测试方法可验证静态工作环境下，混合脉冲功率特性(Hybrid Pulse Power Characterization，HPPC)测试法和多参数联合约束算法对动力电池的实际最大放电功率和最大充电功率的预测。恒流脉冲实验的电压及电流如图13所示。

图13 恒流脉冲充、放电测试的电压与电流Fig.13 Voltage and current in constant current pulse test

图14、图15将HPPC法与多参数联合约束算法预测得到的峰值功率结果进行了对比。可看出，随着放电过程的深入，电池峰值功率逐渐减小，其主要原因是其剩余电量的减少和端电压的降低。对比图14a中的两条曲线可看出，两种预测方法在SOC中段相差不多，而在低SOC 和高SOC时，传统HPPC法得出的结果高于多参数联合约束算法的结果，这是因为传统HPPC法没有考虑最低SOC的限制和最大电流的限制。

图14 最大放电功率对比及最大放电电流Fig.14 Maximum discharge power comparison and maximum discharge current

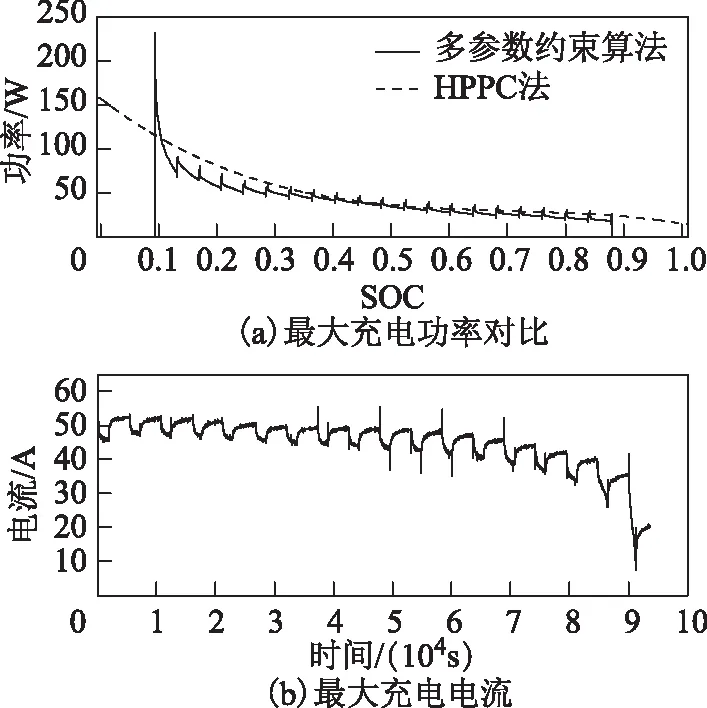
图15 最大充电功率对比及最大充电电流Fig.15 Maximum charge power comparison and maximum charge current

图15a为两种预测方法的充电峰值功率预测结果对比，与放电实验的结果类似：由于没有SOC及最大电流的限制，在SOC>90%时，HPPC法的充电功率明显高于多参数联合约束算法，在这种情况下若以较大的电流充电，则会导致电池过度充电，进而对电池产生损害。多参数联合约束算法在SOC>90%时，充电功率很快下降直至0，能够起到保护电池的作用。同时可发现，电池的充电功率与放电功率是一对矛盾，即电池在低电量的时候充电能力明显大于放电能力。

最后，使用恒功率脉冲放电法在室温条件下对电池的10 s持续峰值放电功率进行测试，以检验HPPC法与采用本文所述的数学模型和多参数联合约束算法估计出的峰值功率的精确度。恒功率放电法测试过程繁琐，对设备要求较高，但测试得到的数据准确，所以此方法通常用来检测功率估计值的准确性。

该方法采用一组型号及老化程度相同的电池，分别测试电池SOC在10%、20%、…、90%、100%时的恒功率放电能力。以SOC=70%为例，测试步骤如下。

1)将电池充电至70%SOC后进行10 s的恒功率放电，记录放电10 s后电池的端电压。

2)若此时电池电压大于(小于)截止电压，则将电池重新充电至70%后，逐步加大(减小)输出功率继续测试，直到电池在70%SOC时放电10 s后达到截止电压，则此时的功率即为电池的输出峰值功率。

3)实验中设定输出功率从电池的额定功率开始，之后按10 W梯度变化。若峰值功率落在两个梯度功率之间，则使用二分法在两梯度功率之间取值，继续测试直至同时满足截止电压与时间的要求。

动力锂离子电池应用于电动汽车领域时，电池的工作特点是工作电流变化剧烈，所以相对于静态工作环境，对动态环境下电池的充、放电性能进行预测更加重要。本文在DST工况下对HPPC法和多参数联合约束算法的预测结果进行比较验证，电池的放电功率如图16所示，放电功率误差如图17所示。

图16 DST工况下的电池放电功率Fig.16 Discharge power in DST condition

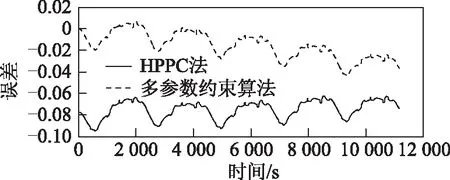
图17 放电功率误差Fig.17 Error of discharge power

由图16可看出，在DST工况下，HPPC法估计结果高于多参数约束方法的预测结果，其原因与恒流脉冲情况下类似。本文提出的多参数约束算法对电池的放电条件限制更为严格，从SOC、电压、电流的角度同时对电池的峰值功率进行限制，令电池在一定范围内工作，从而在最大程度释放电池能量的情况下保证了其安全性。而将滞回环节引入电池模型，又使得模型在电动汽车的复杂工况下有更好的表现，提升了该方法在复杂工况下的准确性。从图17中的误差曲线可看出，本文提出的方法比HPPC法有更高的精确度。

4 结论

本文针对锂离子电池充、放电过程中的滞回特性提出一种基于滞回特性的锂离子电池动态模型，并利用H∞滤波算法将上述模型应用到锂离子电池的SOC估计中，降低了电动车动态工况下SOC估计过程中的模型误差和算法误差。同时利用SOC估计结果及电池电压、电流的约束来预测出电池10 s最大充、放电功率。最后通过与恒功率放电实验数据的比较，验证了这种方法在预测电池SOP时具有较高的准确性。

针对锂离子电池SOP验证实验的分析可得出如下结论：

1)随着锂离子电池放电过程的进行，其峰值功率逐渐减小，而在放电末端其峰值功率迅速衰减，因此锂离子电池在放电末端时，电动汽车需限制电池的放电功率，防止电池寿命受损；相反，在锂离子电池充电工况下，随着充电的进行，其充电功率逐渐减小，在充电末端应该限制电池的充电电流。

2)在电池的放电过程中，锂离子电池的峰值功率与其端电压呈一致相关性，因此在一定程度上可用锂离子电池端电压表征其峰值功率。而在放电末端，相对于端电压而言，锂离子电池的功率衰减更快，此时如果仅通过端电压来确定电池性能，会对系统安全与电池寿命产生影响。

3)混合脉冲HPPC法运用广泛，在静态工作环境或对预测精度要求不高的情况下是一种比较方便的方法，但在动态工作环境下，应采用更精确的模型，考虑更多参数的限制来进行功率预测。

[1] Joo G K，Byungrak S，el al.A review of lithium and non-lithium based solid state batteries[J].Journal of Power Sources，2015，282(15)：299-322.

[2] Chen Xiaopeng，Shen Weixiang，Cao Zhenwei，et al.Adaptive gain sliding mode observer for state of charge estimation based on combined battery equivalent circuit model[J].Computers & Chemical Engineering，2014，64(18)：114-123.

[3] Dai Haifeng，Guo Pingjing，Wei Xuezhe，et al.ANFIS (adaptive neuro-fuzzy inference system) based online SOC (State of Charge) correction considering cell divergence for the EV (electric vehicle) traction batteries[J].Energy，2015，80：350-360.

[4] 连湛伟，石欣，克潇，等.电动汽车充换电站动力电池全寿命周期在线检测管理系统[J].电力系统保护与控制，2014，42(12)：137-142.

Lian Zhanwei，Shi Xin，Ke Xiao，et al.The whole life cycle on-line detection and management of system of power battery in the electric vehicle charging and exchanging station[J].Power System Protection and Control，2014，42(12)：137-142.

[5] 于海芳，逯仁贵，朱春波，等.基于安时法的镍氢电池SOC估计误差校正[J].电工技术学报，2012，27(6)：12-18.

Yu Haifang，Lu Rengui，Zhu Chunbo，et al.State of charge estimation calibration for Ni-MH battery based on ampere-hour method[J].Transactions of China Electrotechnical Society，2012，27(6)：12-18.

[6] Weng Caihao，Sun Jing，Peng Huei.A unified open-circuit-voltage model of lithium-ion batteries for state-of-charge estimation and state-of-health monitoring[J].Journal of Power Sources，2014，258(14)：228-237.

[7] 雷肖，陈清泉，刘开培，等.电动车电池SOC估计的径向基函数神经网络方法[J].电工技术学报，2008，23(5)：81-87.

Lei Xiao，Chen Qingquan，Liu Kaipei，et al.Radial-based-function neural network based SOC estimation for electric vehicles[J].Transactions of China Electrotechnical Society，2008，23(5)：81-87.

[8] Kalman R E.A new approach to linear filtering and prediction problems[J].Journal of basic Engineering，1960，82(1)：35-45.

[9] 胡益，王晓茹，李鹏，等.静止同步串联补偿器(SSSC)的非线性鲁棒H∞控制策略研究[J].电力系统保护与控制，2015，43(7)：30-36.

Hu Yi，Wang Xiaoru，Li Peng，et al.Nonlinear robust strategy static synchronous series compensator (SSSC) of H∞ control[J].Power System Protection and Control，2015，43(7)：30-36.

[10]Gholizadeh M，Salmasi F R.Estimation of state of charge，unknown nonlinearities，and state of health of a lithium-ion battery based on a comprehensive unobservable model[J].IEEE Transactions on Industrial Electronics，2014，61(3)：1335-1344.

[11]赵又群，周晓凤，刘英杰.基于扩展卡尔曼粒子滤波算法的锂电池 SOC 估计[J].中国机械工程，2015，26(3)：394-397.

Zhao Youqun，Zhou Xiaofeng，Liu Yingjie.SOC estimation for Li-ion battery based on extended Kalman particile[J].China Mechanical Engineering，2015，26(3)：394-397.

[12]刘金枝，杨鹏，李练兵.一种基于能量建模的锂离子电池电量估算方法[J].电工技术学报，2015，30(13)：100-107.

Liu Jinzhi，Yang Peng，Li Lianbing.A method to estimate the capacity of the lithium-ion battery based on energy model[J].Transactions of China Electrotechnical Society，2015，30(13)：100-107.

[13]赵淑红，吴锋，王子冬，等.动力电池功率密度性能测试评价方法的比较研究[J].兵工学报，2009，30(6)：764-768.

Zhao Shuhong，Wu Feng，Wang Zidong，et al.Study on the different test methods for power density of power batteries[J].Acta Armamentarii，2009，30(6)：764-768.

[14]刘莎，卢世刚，庞静.锂离子动力电池脉冲功率特性的研究[J].电源技术，2009，33(4)：276-279.

Liu Sha，Lu Shigang，Pang Jing.Study on pulse power characteristics of lithium ion power battery[J].Chinese Journal of Power Sources，2009，33(4)：276-279.

[15]Dees D，Gunen E，Abraham D，et al.Electrochemical modeling of lithium-ion positive electrodes during hybrid pulse power characterization tests[J].Journal of the Electrochemical Society，2008，155(8)：A603-A613.

[16]孙丙香，姜久春，韩智强，等.基于不同衰退路径下的锂离子动力电池低温应力差异性[J].电工技术学报，2016，31(10)：159-167.

Sun Bingxiang，Jiang Jiuchun，Han Zhiqiang，et al.The lithium-ion battery low temperature stress based on different degradation paths[J].Transactions of China Electrotechnical Society，2016，31(10)：159-167.

[17]Fleischer C，Waag W，Heyn H M，et al.On-line adaptive battery impedance parameter and state estimation considering physical principles in reduced order equivalent circuit battery models：Part 1.Requirements，critical review of methods and modeling[J].Journal of Power Sources，2014，260(15)：276-291.

[18]孙丙香，高科，姜久春，等.基于ANFIS和减法聚类的动力电池放电峰值功率预测[J].电工技术学报，2015，30(4)：272-280.

Sun Bingxiang，Gao Ke，Jiang Jiuchun，et al.Research on discharge peak power prediction of battery based on ANFIS and subtraction clustering[J].Transactions of China Electrotechnical Society，2015，30(4)：272-280.

[19]陈息坤，孙冬，陈小虎.锂离子电池建模及其荷电状态鲁棒估计[J].电工技术学报，2015，30(15)：141-147.

Chen Xikun，Sun Dong，Chen Xiaohu.Modeling and state of charge robust estimation for lithium-ion batteries[J].Transactions of China Electrotechnical Society，2015，30(15)：141-147.

[20]马丽萍，夏保佳.混合电动车用动力MH-Ni电池的研究现状与发展[J].电源技术，2003，27(增刊1)：245-249.

Ma Liping，Xia Baojia.State-of-art of R & D of power Ni-MH battery for hybrid electric vehicle[J].Chinese Journal of Power Sources，2003，27(S1)：245-249.

[21]Plett G L.High-performance battery-pack power estimation using a dynamic cell model[J].IEEE Transactions on Vehicular Technology，2004，53(5)：1586-1593.

[22]刘艳莉，戴胜，程泽，等.基于有限差分扩展卡尔曼滤波的锂离子电池SOC估计[J].电工技术学报，2014，29(1)：221-228.

Liu Yanli，Dai Sheng，Cheng Ze，et al.Estimation of state of charge of lithium-ion battery based on finite difference extended Kalman filter[J].Transactions of China Electrotechnical Society，2014，29(1)：221-228.

[23]岳晓奎，袁建平.H∞滤波算法及其在GPS/SINS组合导航系统中的应用[J].航空学报，2001，22(4)：366-368.

Yue Xiaokui，Yuan Jianping.H∞ filtering algorithm and its application in GPS/SINS integrated navigation system[J].Acta Aeronautica ET Astronautica Sinica，2001，22(4)：366-368.

[24]胡再刚.基于H∞的传递对准方法研究[D].哈尔滨：哈尔滨工程大学，2007.

[25]秦永元.卡尔曼滤波与组合导航原理[M].西安：西北工业大学出版社，1998.

[26]秦琴，侯明善，杨常伟.自调节鲁棒H∞滤波目标机动估计[J].电光与控制，2007，14(2)：30-33.

Qin Qin，Hou Mingshan，Yang Changwei.Target maneuvering estimations using H∞ filter and self-tuning second-order Markov process model[J].Electronics Optics & Control，2007，14(2)：30-33.

(编辑 张洪霞)

Method for Estimation of State of Charge and Power Prediction of Lithium-Ion Battery

ChengZe1SunXingmian1ChengSilu2

(1.School of Electrical and Information Engineering Tianjin University Tianjin 300072 China 2.Institute of microelectronics Tianjin University Tianjin 300072 China)

In order to estimate the state of charge (SOC) of lithium-ion battery precisely and predict the actual maximum charge/discharge power of the battery，a second-order RC hysteresis model was established based on the hysteresis phenomena which appeared during the charge-discharge process.The H∞ filter algorithm was used to estimate SOC，which avoided the error caused by the statistical characteristics of noise.This method greatly reduces the model error and algorithm error，and improves the robustness of parameter estimation.Regard the battery voltage，current and the estimation of SOC as constraint conditions to predict the actual maximum charge-discharge power of the lithium-ion battery.Compared with the hybrid pulse power characterization (HPPC) method，the pulse charge-discharge experiments showed that the method proposed had higher accuracy in estimating the battery power.

Lithium-ion battery，battery model，state of change，state of power

国家自然科学基金项目资助(61374122)。

2016-04-26 改稿日期2017-01-17

10.19595/j.cnki.1000-6753.tces.160557

TM911

程 泽 男，1959 年生，教授，研究方向为动力电池组安全评估与故障诊断。

E-mail：chengze@tju.edu.cn(通信作者)

孙幸勉 女，1992 年生，硕士研究生，研究方向为锂离子电池SOC估计。

E-mail：731569462@qq.com