DEM辅助下的倾斜航摄影像匹配方法

常 越，邓 非，2，李天烁

(1.武汉大学 测绘学院，湖北 武汉 430079； 2.国家领土主权与海洋权益协同创新中心，湖北 武汉 430079)

DEM辅助下的倾斜航摄影像匹配方法

常 越1，邓 非1，2，李天烁1

(1.武汉大学 测绘学院，湖北 武汉 430079； 2.国家领土主权与海洋权益协同创新中心，湖北 武汉 430079)

在倾斜航空摄影测量中，倾斜影像间由于视角差异较大，具有较大几何变形，而具备仿射尺度不变性的ASIFT算法存在效率较低的问题，提出一种DEM辅助下的倾斜航摄影像匹配方法。该方法通过利用影像的粗略外方位元素和测区的DEM数据，首先对倾斜影像进行仿射变换来减弱几何变形；然后通过SIFT特征匹配算法来获取同名点对，并使用RANSAC剔除误匹配；最后将同名点对根据单应矩阵反算回原影像，以基础矩阵估计法剔除误匹配，获得最终匹配点对。通过对多组数据进行实验，结果表明，该算法的计算效率较高，获得的匹配点对在数量和分布情况上也更为理想。

倾斜影像匹配；DEM；仿射变换；尺度不变特征变换算法；误匹配剔除

倾斜航空摄影测量突破了传统摄影测量垂直拍摄获取影像的作业模式，凭借其多视角的摄影方式，可获得丰富的建筑物立面信息，且成果满足三维数字城市建设的需要，因而在近年来得到了广泛地推广和应用，成为当前城市自动三维建模的热点技术[1-7]。但与此同时，通过该方法获得的倾斜影像，存在局部几何变形大、影像间具有较大仿射畸变、地物遮挡及影像分辨率不一致等问题，这些问题对影像之间的匹配造成困难。因此，如何从倾斜影像中快速、准确地获取可靠的同名点对，是倾斜航空摄影测量技术的关键问题之一，也是制约着倾斜航空摄影测量技术发展的重要原因[8]。

根据倾斜航空摄影测量成像的特点，倾斜影像的匹配方法应该具备仿射不变[9]、旋转不变以及尺度不变的特性。目前，主流的匹配方法有Harris-Affine特征匹配、Hessian-Affine特征匹配以及MSER(最稳定极值区域)算法等对原始的倾斜影像进行仿射不变性区域提取，再进行描述匹配的方法[10]。其中，Harris-Affine特征匹配[11]在匹配前要先进行Harris角点检测，然后通过迭代求出仿射不变区域，并剔除不稳定点对，得到具有仿射不变性的Harris特征点。Hessian-Affine特征匹配[12]也类似于此，不同之处在于使用了Hessian算子检测，更倾向于斑点特征。而MSER算法则是通过对比极大稳定区域(仿射不变区域)描述符来获取同名点对。这三种方法效率较高，但匹配得到的点对数量偏少，在处理视角变化较大的影像时，匹配效果并不理想，甚至无正确匹配点对。此外，Affine Scale Invariant Feature transform (ASIFT)特征匹配是通过垂直和水平方向上的旋转模拟现实的仿射变换，生成系列模拟影像后再进行SIFT特征点的提取和描述。该方法规范化了六个仿射变换参数，对于影像的旋转、缩放、光照的变化有较强的鲁棒性[13]，对倾斜影像的匹配效果较好，但是由于针对序列模拟影像的匹配非常耗时，效率较低，因此难以直接应用到实际项目中去。

对于ASIFT算法复杂度高，效率低的问题，可以考虑引入影像粗略外方位元素，生成少量模拟影像，以提高影像匹配效率。倾斜影像与垂直影像或倾斜影像间因拍摄角度的差异，存在着较大的几何畸变、尺度差异以及旋转变化，因此，本文提出了一种DEM辅助下的倾斜航摄影像匹配方法，该方法利用了倾斜影像粗略的外方位元素以及航摄区域的DEM数据(本文采用免费的低分辨率DEM数据)，首先通过将倾斜影像投影到摄区的DEM上，对倾斜影像进行仿射纠正，然后再进行SIFT(scale invariant feature transform)特征匹配[14]，并对匹配点对中的误匹配进行剔除。

此外，本文在进行仿射纠正前，首先通过求解地面投影线框间的重叠度，自动挑选出重叠度超过阈值的影像进行匹配，从而建立影像间的相互关联性，为批量影像间的匹配提高效率。同时，本文仿射纠正获得的影像也是根据计算重叠线框获取的重叠区域的影像(重叠区域含有缓冲区)，这对后面的SIFT匹配过程也起到了提高效率的作用。

1 算 法

算法的实现过程如图1所示，主要分为三个阶段：①DEM辅助下的倾斜航摄影像仿射纠正，获取原始影像重叠区域纠正后的影像；②对纠正后的影像进行SIFT特征匹配和RANSAC法剔除错误点对，得到同名点对；③将同名点对根据单应矩阵反算回原影像，以基础矩阵估计法剔除误匹配，获得最终结果。

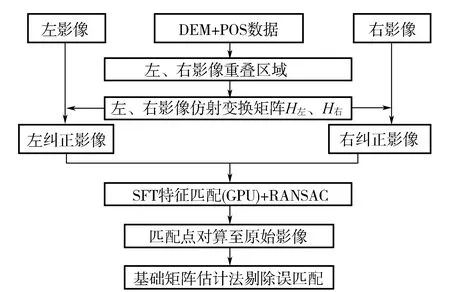
图1 匹配算法流程

1.1 DEM辅助下的倾斜航摄影像仿射纠正

倾斜航摄影像的突出特点就是由多角度拍摄而得，不同拍摄角度得到的影像间具有较大仿射畸变。因此DEM辅助的倾斜影像仿射纠正就是为了减弱这种变形，提高匹配的可靠性与效率。需要的初始数据包括：待匹配的左右影像、影像的粗略外方位元素、以及低分辨率的测区DEM(可通过免费数据源获取，其坐标系应与外方位元素坐标系相同)。

1)首先根据影像的粗略外方位元素，分别将左、右影像投影到测区的DEM上，即求解摄影光束与DEM的交点(如图2所示)，得到左、右影像上的点对应的物方坐标(Xi,Yi,Zi)。

图2 摄影光束与DEM相交示意图

2)根据求得的影像物方坐标的平面坐标值Xi，Yi，可得到左、右影像的地面投影线框，从而求得左、右影像的重叠区域，得到重叠区域的AABB包围盒，并给予一定的缓冲区，形成纠正后影像的覆盖区域S。

3)保持该区域(含缓冲区)地面投影线框的几何特征，根据垂直影像的分辨率，将其按比例缩放至影像，此时，纠正后影像的四个顶点对应于原影像的四点(xi,yi)，可通过物方点坐标(Xi,Yi,Zi)利用共线方程反算求得(四个顶点的物方点即为纠正后影像的覆盖区域S的四个角点)：

(1)

式中:Xs,Ys,Zs为外方位线元素;a1,a2,a3,b1,b2,b3,c1,c2,c3可由外方位角元素求得。然后根据这四点在原影像和纠正后影像的坐标关系，分别计算出左、右影像仿射变换矩阵H左,H右。

4)进行仿射变换，得到左、右影像变换后的影像。并对影像中的无效点(变换时未进行赋值的像元)，进行判断并插值计算。

以如图3所示的倾斜影像(a)和下视影像(b)为例进行试验，从纠正后的影像图(c)、(d)可以看出：通过该方法，可以有效地减弱几何和尺度上的变形，便于后面的影像匹配。此外，本文方法得到变换后的影像仅为重叠区域，这对后续的匹配无论在准确度上还是在效率上都能起到良好的作用。

图3 DEM辅助下的倾斜影像仿射纠正示例

1.2 SIFT特征匹配

在完成仿射纠正变换后，本文采用对尺度缩放、旋转、亮度变化都具备较强抵抗性的SIFT特征匹配算法对两张纠正后的影像进行匹配。匹配的过程包含两个阶段：SIFT特征向量的提取和SIFT特征向量的匹配[15]。

特征的提取可以概括为以下4个步骤：

第一步，通过高斯滤波函数来构建尺度空间L(x,y,σ)，并通过计算高斯差分(DOG)尺度空间来检测潜在的极值点。其中高斯差分算子式为

(2)

第二步，通过对尺度空间函数的泰勒展开来精确极值点在尺度空间的位置，在该步骤中，低对比度点将被过滤且关键点的边缘响应将被消除，以提高稳定性。

第三步，进行方向的分配。按照高斯加权的方法统计特征点区邻域像素的梯度方向直方图，该直方图的峰值就是特征点的主方向。对此，特征点的描述时就可以主方向为依据，以确保旋转的不变性。

第四步，生成SIFT特征向量，实质上生成一个128维的代表着高斯加权的邻域划分区块梯度方向和大小的向量。

SIFT特征向量的匹配以特征向量间的欧氏距离为相似性度量，通过将距离最小点与距离第二小点间的比值与阈值进行对比来判断是否为正确的匹配。

传统的SIFT特征匹配算法是由CPU串行实现，本文为提高匹配的效率，选用了GPU进行并行加速，与CPU混合实现整个算法过程[16]，加快算法的运行。

1.3 误匹配剔除

尽管SIFT特征匹配具有一定的稳定性，其匹配的结果中仍存在一些误匹配点对，需要进行剔除。本文首先采用随机抽样一致性(RANSAC)算法，对纠正后影像的误匹配点对进行初始剔除。然后将经过初步去除误匹配的同名点对根据本文1.1节的逆步骤，将同名点对分别反算回原始影像，得到其在原始影像上的点坐标值。再利用基础矩阵(fundamental matrix)估计法对同名点对进行筛选，得到最终结果。

2 实验与效果分析

2.1 实验准备

为证明上述方法的有效性，本文使用VS2010实现了该算法，并选取了一套贵州省六盘水市的倾斜航摄影像进行了测试。这套数据由航空摄影测量仪获取，分为下视影像和多组倾斜影像，影像大小为6 000像素×4 000像素。在这里，列举了3张具有代表性的城区范围的影像，如图4所示。其中，影像(a)和(b)为视角不同的两张倾斜影像，倾斜影像1为后视影像，倾斜影像2为左视影像，影像(c)为下视影像。程序的运行环境为：Windows 7、GTX960、16G、i7-CPU。

图4 实验数据缩略图

对于倾斜影像间的匹配，大致可以分为三类：不同视角的倾斜影像与倾斜影像的匹配、倾斜影像与下视影像的匹配以及下视影像与下视影像的匹配。而下视影像间仿射畸变小、匹配效果较好，不作为本文考虑内容。因此，根据上面列举的3张影像，本文的实验可分成以下两组进行：①下倾斜影像1和下视影像；②倾斜影像1和倾斜影像2。并对这两组数据分别利用SIFT算法、ASIFT算法以及本文算法所得到的匹配结果进行对比分析。对匹配结果进行评价时，既要考虑匹配的效果，又要考虑匹配的效率，因此匹配的标准包括以下三个部分：匹配点对的数量与分布、匹配点对的正确率以及匹配过程的耗时。其中匹配点对是否正确需要在ENVI 软件中逐对的人工目视检查和判断(城区影像具有多平面场景，因而不能简单地通过计算出均方根误差来判断匹配点对的正确性)。

2.2 实验结果与分析

通过三种方法得到的匹配结果如图5所示，将匹配相关结果进行统计可得到表1，从图5和表1的结果可以发现：①采用本方法得到的正确点对数分别是SIFT算法和及ASIFT算法的约7倍和5倍左右，且从匹配点对的分布情况来看，采用本文方法所得到同名点对分布更加均匀。②ASIFT算法针对倾斜影像的匹配正确率较高，本文算法略优于ASIFT算法，而SIFT算法对不同倾角的倾斜影像匹配效果较差，这也是说明了其并不具备仿射不变性。③从匹配效率来看，SIFT算法的效率最高；而ASIFT算法由于匹配算法复杂度较高，匹配过程耗时非常大，效率非常低；相比而言，采用本文的方法，效率较高。

图5 三种方法分别对两组数据的匹配效果

表1 三种方法分别对两组数据的匹配结果

通过对实验结果的分析，本文提出的方法要优于SIFT算法和ASIFT算法。由于通过利用摄区低分辨率DEM和影像初始外方位元素对影像进行了仿射变换，减弱了倾斜影像间的几何变形，使算法具有仿射不变性，可获得更为准确的匹配结果，与此同时，算法在复杂度上要比ASIFT算法简单的多，所以在效率上得到很明显地提高。

3 结束语

本文针对倾斜影像间几何变形较大的问题，提出了一种DEM辅助下的倾斜航摄影像匹配方法。该方法首先通过将影像投影到摄区的DEM上实现对倾斜影像的仿射纠正以削弱几何上的变形，然后将经过SIFT特征匹配和RANSAC误匹配剔除后的匹配点对反算回原始影像，再利用基础矩阵估计法剔除误匹配，得到最终的同名点对。经实验验证，该方法匹配的效率远高于ASIFT匹配算法，且从匹配得到的点对数量、分布及正确率来看，匹配效果较好。下一步可针对SIFT算法内部进行优化，如采用具有视点不变性的Harris角点来建立SIFT描述符等方法，以达到更好的匹配效果；也可尝试利用数字表面模型(DSM)数据对影像进行仿射变换，对比匹配效果。

[1] RUPNIK E, NEX F, REMONDINO F. Oblique Multi-Camera Systems-Orientation and Dense Matching Issues[J]. ISPRS-International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2014, XL-3/W1(3):107-114.

[2] 王伟, 黄雯雯, 镇姣. Pictometry倾斜摄影技术及其在三维城市建模中的应用[J]. 测绘与空间地理信息, 2011, 34(3):181-183.

[3] 杨国东, 王民水.倾斜摄影测量技术应用及展望[J].测绘与空间地理信息,2016,39(1):13-15,18.

[4] HÖHLE J. Oblique Aerial Images and Their Use in Cultural Heritage Documentation[J]. ISPRS - International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2013, xl-5/w2(XL-5/W2).

[5] 李镇洲, 张学之. 基于倾斜摄影测量技术快速建立城市三维模型研究[J]. 测绘与空间地理信息, 2012, 35(4).

[6] 王卿, 郭增长, 李豪,等. 多角度倾斜摄影系统三维量测方法研究[J]. 测绘工程, 2014, 23(3):10-14.

[7] 杨国东, 王民水. 倾斜摄影测量技术应用及展望[J]. 测绘与空间地理信息, 2016, 39(1):13-15.

[8] WIEDEMANN A, MORÉ J. Orientation Strategies for Aerial Oblique Images[J]. 2012, XXXIX-B1(1):1-33.

[9] MIKOLAJCZYK K，CORDELIA S. A Performance Evaluation of Local Descriptors[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，2005，27(10)：1 615-1 630

[10] MIKOLAJCZYK K, TUYTELAARS T, SCHMID C, et al. A Comparison of Affine Region Detectors[J]. International Journal of Computer Vision, 2005, 65(1-2):43-72.

[11] MIKOLAJCZYK K，CORDELIA S. Scale and Affine Invariant Interest Point Detectors[J]. International Journalof Computer Vision，2004，60(1)：63_86

[12] MIKOLAJCZYK K，SCHMID C. An Affine Invariant Interest Point Detector[J]. Lecture Notes in Computer Science，2002，2 350：128_142

[13] MOREL J M, YU G. ASIFT: A New Framework for Fully Affine Invariant Image Comparison[J]. Siam Journal on Imaging Sciences, 2009, 2(2):438-469.

[14] LOWE D G. Distinctive Image Features from Scale-Invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(60):91-110.

[15] 王佩军. 摄影测量学:测绘工程专业[M]. 武汉：武汉大学出版社, 2005.

[16] 王瑞, 梁华, 蔡宣平. 基于GPU的SIFT特征提取算法研究[J]. 现代电子技术, 2010, 33(15):41-43.

[责任编辑：李铭娜]

Matching method for oblique aerial image assisted by DEM

CHANG Yue1, DENG Fei1，2, LI Tianshuo1

(1.School of Geodesy & Geomatics,Wuhan University,Wuhan 430079,China； 2.Collaborative Innoation Center for Territorial Sovereignty and Maritime Rights,Wuhan University,Wuhan 430079,China)

In the oblique aerial photogrammetry, the oblique images have large geometric deformation due to the great differences of the viewing angles. However, the algorithm with affine scaling invariance like ASIFT algorithm is less efficient. Therefore, this paper presents a DEM-assisted oblique aerial image matching method. Firstly, the geometrical deformation is weakened by affine transformation of the oblique image by making full use of the rough Exterior Orientation (EO) elements and DEM data. Secondly, Scale Invariant Feature Transform ( SIFT) algorithm is used to match the corrected images to get the corresponding points, and then the false matches in them are eliminated by using the RANdom SAmple Consensus (RANSAC) algorithm．Finally, the homography matrix is used to calculate the corresponding point coordinates on the original image, and the mismatches are eliminated with Fundamental Matrix Estimation method in order to obtain the final corresponding points. Experiments conducted on many sets of oblique images demonstrate that the corresponding points obtained by the proposed algorithm are significantly improved in the computation efficiency, quantity and distribution.

oblique image matching；DEM；affine transformation；scale invariant feature transform(SIFT)；mismatching elimination

著录：常越，邓非，李天烁，等.DEM辅助下的倾斜航摄影像匹配方法[J].测绘工程，2017，26(11)：18-22.

10.19349/j.cnki.issn1006-7949.2017.11.004

2016-10-18

国家自然科学基金资助项目(41271431，41401536)；国家科技支撑计划课题(2012BAJ23B03).

常 越(1993-)，女，硕士研究生.

邓 非(1976-)，男，教授，博士.

TP75

A

1006-7949(2017)11-0018-05