基于流固耦合试验的k-n表达式探讨

李正辉，王世梅,1b,2，郭 振，鲁 芃，金来福

(1.三峡大学 a.土木与建筑学院；b.三峡库区地质灾害教育部重点实验室，湖北 宜昌 443002；2.三峡地区地质灾害与生态环境湖北省协同创新中心，湖北 宜昌 443002)

基于流固耦合试验的k-n表达式探讨

李正辉1a，王世梅1a,1b,2，郭 振1a，鲁 芃1a，金来福1a

(1.三峡大学 a.土木与建筑学院；b.三峡库区地质灾害教育部重点实验室，湖北 宜昌 443002；2.三峡地区地质灾害与生态环境湖北省协同创新中心，湖北 宜昌 443002)

k-n关系是岩土工程流固耦合分析计算中的一个关键表达式，常规的室内渗透试验由于没有考虑到渗流过程中的流固耦合效应，因而得到的k-n关系与实际情况有偏差。为得到更精确的k-n关系，采用自主研发的SRS-1型渗流和蠕变耦合试验仪开展了各种不同固结压力下的三轴流固耦合试验，获得了渗流过程中土样孔隙率随时间的变化曲线，拟合得到了考虑流固耦合与不考虑流固耦合的k-n表达式，并对考虑流固耦合、不考虑流固耦合及Kozeny-Caman经验公式给出的3种k-n表达式进行了对比分析。将3种表达式分别用于考虑流固耦合效应的一维饱和地基固结的数值模拟，将计算结果与非流固耦合方法计算结果进行比较。结果表明：渗流过程中土的孔隙率是动态变化的，为得到更精确的k-n关系，应考虑渗流过程中的流固耦合效应；工程中的土体固结问题实际是一个流固耦合问题，不能按非流固耦合方法计算，否则产生的误差非常大；当前流固耦合数值模拟中被广泛使用的Kozeny-Caman经验公式不能很好地反映黏土k-n的关系，在数值计算中造成的误差非常大，因此不建议使用；为了提高数值模拟结果的准确性，建议采用考虑流固耦合效应的k-n表达式。

流固耦合；渗流试验；k-n关系；数值模拟；地基固结

1 研究背景

渗透系数是描述土体渗流和固结的基本参数，对于同一种饱和土而言，在不考虑温度影响的条件下，渗透系数只与土的孔隙率有关[1]。在考虑流固耦合的数值模拟中，渗透系数k-孔隙率n的关系(文中简称为k-n表达式)，是一个至关重要的表达式[2]。

为获得k-n表达式，通常的做法是通过常规的室内渗透试验针对不同初始孔隙率的土样分别开展渗流试验，得到不同初始孔隙率对应渗流稳定时的渗透系数[3-4]。然而渗流和土体骨架变形是相互影响的，这个过程称为流固耦合[5]。在实际的渗流过程中，由于土样的孔隙水压力发生变化，引起土骨架的有效应力变化，导致土骨架的变形，使土样的孔隙率发生变化，因此常规渗透试验测得的渗透系数并不对应于土样初始孔隙率，而是对应于因流固耦合效应产生了骨架变形之后的孔隙率。因此，常规方法获得的k-n关系表达式与实际情况存在偏差。

本次试验采用SRS-1型渗流和蠕变耦合试验仪，试验中可计算渗流之前的初始孔隙率n0和渗流稳定之后(即因流固耦合效应土骨架产生变形)的孔隙率n1，并测得土样渗流稳定后的渗透系数;分别对不同围压固结稳定后的土样进行渗流试验，便可获得多组初始孔隙率n0、渗流稳定后的孔隙率n1及渗透系数k的数据;对多组数据进行拟合得到不考虑流固耦合效应的k-n0表达式、考虑流固耦合效应的k-n1表达式，并以一维饱和地基固结为算例，分别采用上述考虑流固耦合的k-n1表达式、不考虑流固耦合效应的k-n0表达式和当前广泛使用的Kozeny-Caman 建立的k-n经验公式[6-7]，进行流固耦合数值模拟，以比较其结果差别，为数值模拟中k-n表达式的选取提供科学依据。

2 试验仪器和操作方法

本次试验采用的仪器为自主研发的SRS-1型渗流和蠕变耦合试验仪，是在三轴蠕变试验仪的基础上改进而成，由双围压室、围压施加及体变测量单元、孔隙水压力传感器、渗透压施加单元、轴向压力施加单元、轴向位移传感器、渗流量测量单元、数据采集单元组成。与三轴蠕变试验仪相比，该仪器增加了渗透压施加单元和渗流量测量单元，用于对土样施加渗流和测量渗流量。仪器由加载装置及压力室和压力控制柜2部分组成，如图1所示。

图1 SRS-1型渗流和蠕变耦合试验仪Fig.1 Seepage and creep coupling test apparatus SRS-1

加载装置及压力室主要包含双压力室、轴向压力施加单元、轴向位移传感器和孔隙水压力传感器，如图2所示。仪器的其他单元设置在压力控制柜中，如图3所示。SRS-1型渗流与蠕变耦合试验仪的优点在于可以得到土样在试验过程中渗透系数和体积变形的实时数据，因此可以得到考虑流固耦合效应的k-n关系。

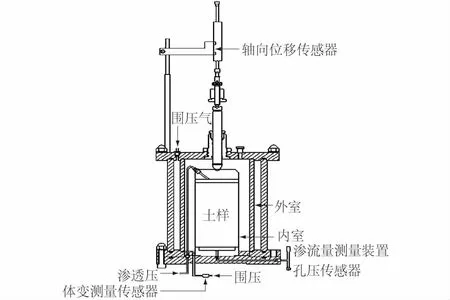
图2 加载装置及压力室Fig.2 Schematic diagram of loading device and pressure cell

图3 压力控制柜Fig.3 Photo of pressure control panel

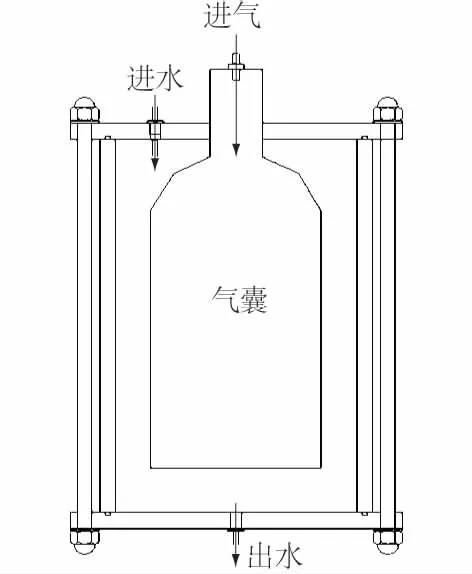
图4 隔离膜水气交换器Fig.4 Schematic diagram of water and air exchanger

隔离膜水气交换器如图4所示。

SRS-1型渗流和蠕变耦合试验仪试验前应做如下操作：

(1) 向水箱中注入蒸馏水至水箱2/3高度处。

(2) 根据试验要求选择围压管量程即选择大围压管或小围压管，选好后通过围压管注水入口向围压管中注入蒸馏水至围压管9/10高度处。

(3) 以气压水的方式将水箱中的水压入到压力控制柜中渗透压施加单元的隔离膜水气交换器中。

(4) 排出所有通水管道中的空气。

(5) 装好土样后，将压力室、轴向压力施加单元和轴向位移传感器固定，转动手轮使杠杆水平。

(6) 将水箱中的水压入到压力室的内室中，使内室充满水。

(7) 将软件中的所有数据清零，准备开始试验。

3 流固耦合试验

3.1 试验试样

试验用土取自于湖北省恩施自治州巴东县某滑坡滑带土，室内测得滑带土基本物理指标见表1，颗粒分布曲线如图5所示。滑带土取回后风干碾散，将碾细的土样过筛，筛孔直径为2 mm，作为试验用土。

表1 土体的基本物理指标

图5 颗粒分布曲线Fig.5 Curve of particle size distribution

三轴试样的横截面直径D=6.18 cm，高H=12.5 cm，通过控制干密度击实成样，然后用饱和架固定抽真空饱和。饱和土样密度ρ=1.95 g/cm3,饱和含水率W=30.69%，初始孔隙率n=0.45。

3.2 试验目的和试验方案

本试验的目的是揭示渗流过程中孔隙水压力及土骨架发生变化的现象，即流固耦合效应，并获得考虑流固耦合效应的k-n关系。

基本思路是：通过施加不同的围压对土样进行排水固结，得到渗流试验的初始孔隙率n0，然后再施加一定的水头压力进行渗流试验，待试样变形稳定及渗流稳定后，可测得土样的体积变化量，并计算出渗流稳定后的孔隙率n1。从而获得土样的渗透系数k和初始孔隙率n0(未考虑流固耦合效应)、渗流稳定后的孔隙率n1(考虑流固耦合效应)的关系。

具体试验方案如表2。

图6 孔隙率和孔隙水压力随时间的变化Fig.6 Variations of porosity and pore water pressure against time

围压/kPa水头压力/kPa围压/kPa水头压力/kPa504020019010090250240150140

逐级施加围压(50，100，150，200，250 kPa)进行排水固结，待每级围压排水固结完成后，施加对应的水头压力(40，90，140，190，240 kPa)进行渗流，即围压50 kPa对应的渗透压40 kPa，围压100 kPa对应的渗透压90 kPa，以此类推。

3.3 试验结果与分析

图6表示围压分别为50,150,200 kPa及其对

应的水头压力分别为40,140,190 kPa时土样孔隙率和试样孔隙水压力随时间的变化曲线。 图中时间均根为时间的开方。

由图6可以看出，从施加渗流水头时刻起，土样孔隙率和孔隙水压力均随时间而增大，达到一定时间后土样孔隙率趋于稳定。这是因为对于固结稳定后的土样施加渗流压力后，土样中孔隙水压力随之增大，根据有效应力原理知土样有效应力相应变小，因此土样体积将增大，土样孔隙率也相应变大。这就是流固耦合现象。

计算得到各级围压固结条件的渗流初始孔隙率n0、渗流稳定孔隙率n1及渗流稳定后的渗透系数k，见表3。

表3 试验结果

然后利用表3中数据分别绘制k-n0和k-n1曲线图，并将当前被广泛采用的由Kozeny-Caman建立的k-n经验公式绘制于同一图中，以比较3条曲线的差别，见图7所示。

图7 土样孔隙率和渗透系数的关系Fig.7 Relationship between porosity and permeability coefficient of soil samples

图7的3条曲线中k-n1代表了土样真实的渗透系数-孔隙率关系。比较3条曲线可看出，不考虑流固耦合k-n0曲线与真实的考虑了流固耦合的k-n1曲线存在一定偏差，而由Kozeny-Caman经验公式得到k-n曲线与k-n1曲线相差很大，由此进一步说明，Kozeny-Caman经验公式对黏土不适用[8]。

通过曲线拟合分别得到土样考虑了流固耦合的k-n1表达式和未考虑流固耦合的k-n0表达式，如式(1)和式(2)。

k=1.011 44×10-8×e41.090 73n1,R2=0.993 44;

(1)

k=1.798 83×10-8×e40.042 27n0,R2=0.993 37。

(2)

Kozeny-Caman建立的k-n经验公式[7]为

(3)

式中k0为初始渗透系数。

4 算例分析

一维饱和地基固结问题是典型的流固耦合问题，随着固结过程中孔隙水压力的消散，地基发生变形，土的孔隙率和渗透系数发生改变，若按经典渗流力学方法(即认为土体固结过程中渗透系数不变)计算此问题显然不符合实际情况。现采用上述3个k-n表达式分别对该问题进行数值模拟计算，并对结果进行比较，以阐述采用不同的k-n表达式对计算结果产生的影响。

4.1 计算模型及材料参数

以一维饱和地基固结为例，土层厚度为10.0 m，土层的初始孔隙率为0.454，底面不排水，顶面单向排水，排出的水立即被抽走，土体表面施加永久荷载400 kPa。土体力学模型采用线弹性模型，弹性模量E=2 MPa，泊松比ν=0.3，水的重度取γw=10 kN/m3。将模型简化为厚10.0 m，宽1.0 m，两侧边界约束x方向位移，底部约束y方向位移的模型，计算模型见图8。

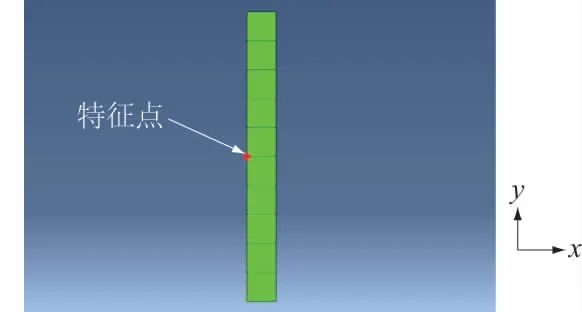
图8 计算模型示意图

4.2 计算结果及分析

选取模型中部一特征点和模型顶面进行分析，图9(a)、图9(b)分别给出了该特征点处的孔隙水压力P和模型顶面竖向位移D随时间的变化曲线。

图9 孔隙水压力和竖向位移随时间的变化曲线Fig.9 Variations of pore water pressure and vertical displacement along with time

由图9可知:

(1) 采用考虑流固耦合效应的k-n1表达式进行流固耦合数值模拟得到的结果，孔隙水压力消散速度最慢，位移减小的速度也最慢，若忽略土的流变现象，可认为该结果为真实结果。

(2) 采用未考虑流固耦合效应的k-n0表达式进行流固耦合数值模拟得到的结果与真实结果有一定误差。

(3) 采用Kozeny-Caman经验公式进行流固耦合数值模拟得到的结果与真实结果有较大误差。

(4) 按经典渗流力学方法进行非流固耦合数值模拟得到的结果与真实结果相差甚远。4种情况的误差主要体现在在固结时间上，考虑流固耦合效应时，固结完成需要12 000 d，采用常规室内渗流试验得出的k-n0表达式计算得到的结果为10 000 d，采用Kozeny-Camen经验公式计算得到的结果为3 000 d，而按经典渗流力学方法进行非流固耦合数值模拟计算得到时间只需要500 d。

以上结果表明，流固耦合问题用经典渗流力学方法进行非流固耦合数值模拟计算，会产生很大误差；对于黏土来说由于Kozeny-Caman经验公式不能很好地反映k-n的关系，在数值计算中造成的误差也很大，因此不建议使用；为了提高数值模拟结果的准确性，k-n表达式建议采用考虑流固耦合效应的渗流试验获取。

5 结 论

(1) 土体渗流过程中孔隙率和孔隙水压力是动态变化的，通过常规渗透试验(忽略渗流过程中的流固耦合效应)得到的k-n关系是不够精确的，为得到更精确的k-n关系，应考虑渗流过程中的流固耦合效应。

(2) 工程中的流固耦合问题应该用考虑流固耦合的数值模拟方法计算，不能按经典渗流力学的方法计算，否则产生的误差非常大。

(3) 考虑流固耦合的数值模拟中当前广泛使用的Kozeny-Caman经验公式不能很好地反映黏土k-n的关系，在数值计算中造成的误差非常大，因此不建议使用。

(4) 为了提高数值模拟结果的准确性，在用到k-n表达式时，建议通过考虑流固耦合效应的渗流试验获得。

[1] 张克恭,刘松玉.土力学[M]. 北京：中国建筑工业出版社, 2001.

[2] 冉启全, 李士伦. 流固耦合油藏数值模拟中物性参数动态模型研究[J]. 石油勘探与开发, 1997, 24(3): 61-65.

[3] 李 平, 骆亚生. 饱和土的三轴渗透试验研究[J]. 路基工程, 2006 ,(6): 32-33.

[4] 柯 瀚, 王文芳, 魏长春, 等. 填埋体饱和渗透系数影响因素室内研究[J]. 浙江大学学报 (工学版), 2013, 47(7): 1164-1170.

[5] 唐延贵. 降雨条件下非饱和土流—固耦合试验与数值研究[D].成都：成都理工大学, 2013.

[6]KLEINBERG R L, FLAUM C, GRIFFIN D D,etal. Deep Sea NMR: Methane Hydrate Growth Habit in Porous Media and Its Relationship to Hydraulic Permeability, Deposit Accumulation, and Submarine Slope Stability[J]. Journal of Geophysical Research: Solid Earth, 2003, 108(B10):429-432.

[7] 王春波, 丁文其, 刘书斌, 等. 各向异性渗透系数随应变场动态变化分析[J]. 岩石力学与工程学报，2014,33(增1)：3015-3021.

[8] SINGH P N, WALLENDER W W. Effects of Adsorbed Water Layer in Predicting Saturated Hydraulic Conductivity for Clays with Kozeny-Carman Equation[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2008, 134(6): 829-836.

(编辑：王 慰)

Expression ofk-nBased on Fluid-solid Coupling Experiment

LI Zheng-hui1,WANG Shi-mei1,2,3,GUO Zhen1,LU Peng1,JIN Lai-fu1

(1.College of Civil Engineering & Architecture, China Three Gorges University, Yichang 443002, China； 2.Key Laboratory of Geological Hazards on Three Gorges Reservoir Area of Ministry of Education, China Three Gorges University, Yichang 443002, China；3. Hubei Provincial Collaborative Innovation Center for Geo-hazards and Eco-environment in Three Gorges Area, Yichang 443002, China)

The expression ofk-nis crucial in the analysis and calculation of fluid-solid coupling problems in geotechnical engineering. The relationship ofk-nobtained from conventional laboratory seepage test deviates from reality as the fluid-solid coupling effect is not considered. To get a more accurate relationship between porosity and permeability coefficient, triaxial fluid-solid coupling test under varying consolidation pressure was conducted on a self-developed SRS-1 seepage and creep coupling test apparatus. The variation of porosity against time was obtained, and the fitted expressions ofk-nwith and without fluid-solid coupling effect are acquired. The expressions together with Kozeny-Caman’s empirical formula were analyzed and then were used in the numerical simulation of one-dimensional saturated foundation consolidation in consideration of fluid-solid coupling. Then the calculation results were compared with the result of classical seepage mechanics method. Results show that 1) fluid-solid coupling effect should be taken into consideration as porosity changes dynamically in the process of seepage; 2) fluid-solid coupling problem should not be solved with classical seepage mechanics method, otherwise the error is too big; 3) since Kozeny-Caman’s empirical formula, which is widely used in numerical simulation of fluid-solid coupling problem, could not accurately reflect the relationship between permeability coefficient and porosity of clay, we do not recommend it for numerical modeling; 4) the expression ofk-nin consideration of fluid-solid coupling effect is recommended to improve the accuracy of numerical simulation results.

fluid-solid coupling; seepage test;k-nrelationship; numerical modeling; consolidation of foundation

2016-05-17；

2016-06-14

国家自然科学基金面上项目(41372359)

李正辉(1993-)，男，湖北武汉人，硕士研究生，主要从事非饱和土力学特性方面的研究工作，(电话)17607186736(电子信箱) lzh1041@163.com。

王世梅(1965-)，女，湖北宜昌人，教授，博士，主要从事岩土力学特性及试验、地质灾害机理及预测评价方面的研究工作，(电话)13972598072(电子信箱)wsm3044@163.com。

10.11988/ckyyb.20160479

2017,34(8):106-110

TU411.4

A

1001-5485(2017)08-0106-05