激光在铝板中激励Lamb波的多参量数值模拟
刘增华,曹丽华,冯雪健,何存富,吴 斌
(北京工业大学 机械工程与应用电子技术学院,北京 100124)
激光在铝板中激励Lamb波的多参量数值模拟
刘增华,曹丽华,冯雪健,何存富,吴 斌
(北京工业大学 机械工程与应用电子技术学院,北京 100124)
运用有限元方法,分析了激光参量和铝板参量对铝板中激光激励Lamb波的影响。通过建立轴对称的激光辐射模型,计算出不同激光能量下的瞬态温度场分布。研究结果表明,激光能量过高会使铝板表面损伤,应控制激光能量,使其低于材料损伤阈值。随后固定激光能量,改变铝板板厚和激光光斑半径的大小,发现光斑半径减小时,Lamb波激发率提高,频带变宽,所含的频谱成分更丰富。
激光;有限元;Lamb波;频谱;铝板
激光超声具有非接触、远距离激发、瞬时、频带宽等特点,在无损检测领域得到越来越广泛的应用[1-4]。为了对材料进行无损评价或检测新材料的性能,必须从理论上理解激光超声的产生、传播过程以及信号的特征。在激光激发超声波的理论研究中,大多采用解析法或数值模拟法。
早期解析法求解热弹性耦合方程主要有本征函数展开法、格林函数法和积分变换法等。WU等[5-6]采用本征函数理论分析了各向同性薄板中激光激励的Lamb波的传播,并研究了各向同性薄板厚度对Lamb波可激励性的影响;但板厚增加时,低阶模态的高频成分和高阶模态的出现造成计算复杂。SPICER等[7]用Laplace-Hankel变换和数值联合反变换分析了各向同性薄板中激光激发Lamb波的传播,进而测量出薄板的弹性模量和厚度,但由于其采用简化模型,与实际激光作用差别较大,同时双积分变换法求解时间-空间坐标系的解比较困难。而格林函数法采用点源模型,忽略了激光的热穿透效应使激光成为表面热源。为解决解析法不准确等问题,利用有限元数值模拟研究激光超声的方法逐渐发展起来,有限元方法有严密的数学理论基础,可比较准确地计算出材料内部形成的瞬态温度场,并能够对结构中的声场分布进行模拟,能清楚描述结构中任一节点的时间位移响应曲线。LEE等[8]建立了激光激励Lamb波的有限元模型,仿真得到了Lamb波位移信号和频谱,以及热辐射附近的温度分布和应力分布。许伯强等[9-11]采用有限元方法分析得出瞬态激光Lamb波的传播特征依赖于接收点距离激励源的位置和相应的频率成分的结论,并得到了距离激励源不同位置的Lamb波的仿真位移波形。关建飞等[12]利用有限元分析法研究了短脉冲、高聚焦的条件下,改变激光光斑半径和脉冲宽度对激光超声导波的影响。
为了综合考虑激光参量和铝板参量对激光激励超声波的影响,笔者基于有限元分析方法,建立轴对称的激光激励超声波模型,定量分析了激光脉冲能量、激光光斑半径及铝板厚度与激光超声Lamb波特征之间的关系。
1 理论基础与数值计算
当脉冲激光辐射在材料表面时,材料表面吸收激光能量并转换成热能,材料表面温度升高,热能主要以热传导的形式向材料内部传递,形成瞬态温度场。温度场的梯度分布产生的热应力作为超声波的激发力源,从而激发出超声波。激光超声激发机制主要包括热弹机制和烧蚀机制。对于烧蚀机制,激光辐射功率密度高于材料表面的损伤阈值(10 MW·cm-2~20 MW·cm-2)时,材料表面的温度急剧升高达到材料的熔点,产生烧蚀现象,会对材料表面造成微米级别的损伤,不适于材料的无损检测;对于热弹机制,激光辐射功率密度低于材料表面的损伤阈值时,材料表面未损伤。因此,激光超声多基于热弹机制[13]。
1.1 热传导方程
脉冲激光辐射材料表面模型如图1所示,脉冲激光垂直辐射在各向同性的金属材料表面,采用圆柱坐标系,金属材料中的热传导方程[13]为
(1)
式中:r为径向半径;z为厚度方向尺寸;T(r,z,t)为t时刻的温度分布;ρ为材料密度;c为比热容;k为导热系数。
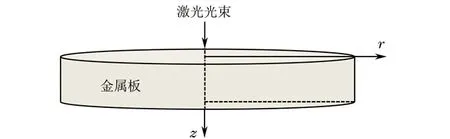
图1 脉冲激光辐射材料表面模型
激光的热作用可以看成加载在材料上表面的边界条件[14],可表示为:
(2)
下表面和侧面满足的绝热条件为
(3)
(4)
式中:R为材料表面的反射系数;r0为设置的材料半径;h为材料的厚度;I0为脉冲激光的辐射功率密度;f(r)及g(t)为脉冲激光的空间分布和时间分布。
激光加热函数的空间分布f(r)采用高斯型函数,可分别表示为
(5)
(6)
(7)
式中:E0为脉冲激光能量;a0为脉冲激光的光斑半径;t0为脉冲激光的有效加热时间。
初始温度为300 K。通过求解满足以上边界与初始条件的热传导方程,可得到材料的温度场分布。
1.2 热弹性方程
以求解的温度场为载荷,在热弹性体中,声波振动位移场可用Navier-Stokes方程[13]表示为
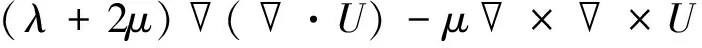
(8)
式中:U(r,z,t)为声场的瞬态位移分布;λ和μ为拉梅常数;α为样品的热膨胀系数。
在上下表面z=0,z=h处应满足自由边界条件
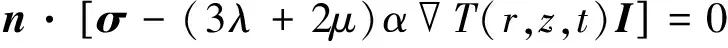
(9)
式中:n为垂直表面的单位向量;I为单位张量;σ为应力张量。
初始条件为:
(10)
通过求解满足边界条件和初始条件的Navier-Stokes方程,可得到金属板中波的位移场。
1.3 有限元形式
有限元形式的热传导方程和控制方程可以分别转化为[14]
(11)
(12)
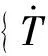
对热弹性体,柱坐标系中外力矢量表示为∫ve[B]T[D]{ε0}dV,[B]T为形函数导数的转置矩阵;[D]为材料特性矩阵;{ε0}为初应变矢量。
式(12)是建立在时刻t的平衡方程,采用Newmark时间积分法,对式(12)进行积分,便可得到时间-位移曲线。假设时间步长为Δt,位移和其一次导数[15]为
(13)
(14)
式中:α和γ为决定积分稳定性和精度的参数。
(15)
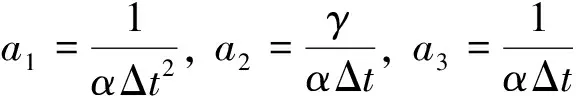
(16)
这样,通过对式(15)不断进行积分,可得到位移-时间曲线。
2 数值模拟结果
2.1 激光和材料的相关参数
仿真采用二维轴对称模型,激光辐射有限元计算模型如图2所示。超声波的激励与接收在同一侧面上,材料为铝板,板厚为0.2 mm,半径为15 mm,铝板的参数分别为:密度2 700 kg·m-3,热膨胀系数2.31×10-5K-1,比热容904 J·kg-1·K-1,导热系数238 W·m-1·K-1,弹性模量70 GPa,泊松比0.35,表面反射系数0.9。设置激光脉冲能量为10 mJ,激光光斑半径a0为600 μm,脉冲持续时间t0为10 ns,在铝材料表面反射系数为0.1的条件下,计算可得激光功率密度约为8.8 MW·cm-2,低于铝板的损伤阈值。
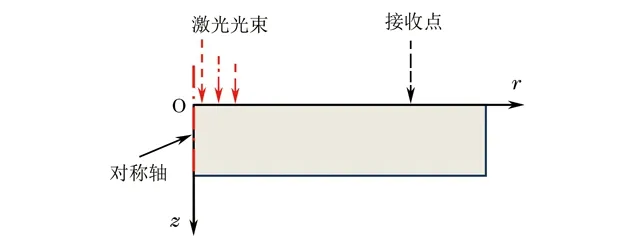
图2 激光辐射有限元计算模型
为了保证热弹控制方程的求解精度及计算效率,合理地选择时间步长和单元大小非常关键。对于单元大小的选取,由于激光作用区域小且在微米级别,网格较密,故采用变网格技术,模型分为激光辐射区域、过渡区域和超声波传播区域。激光辐射区域网格尺寸为1~5 μm,超声波的传播区域为50 μm,过渡区域则采用自由三角形过渡。对于时间步长的选取,激光脉冲持续时间为10 ns,随后温度逐渐达到稳定,故采用变时间步长计算,变化范围为0.1~10 ns。

图3 1 μs时的温度场分布
2.2 瞬态温度场
脉冲激光形成瞬态温度场的梯度分布产生的热应力是超声波的激发力源,因此,精确地计算温度场是准确分析超声波产生过程的基础。图3为1 μs时的温度场分布,可以看出激光辐射在材料表面时,温度最大值分布在材料的表面,直观看到轴向方向(r方向)温度扩散长度大于深度方向(z方向)。图4为激光辐射中心不同深度处温度随时间变化的关系。从图4可见,处于辐射区的材料表面温度迅速升高,在30 ns左右时温度达到最高值470 K(小于铝板的熔点温度),然后由于热传导,热能逐渐向材料内部传递,温度逐渐下降。同时随着距离表面深度的增加,温度上升变得缓慢,峰值也逐步下降,这是典型的热传导特性。10 μm深度处左右,温度不再上升。这表明:激光辐射在金属表面,在表面附近产生一个不均匀分布的瞬态升温区域,由于热传导作用,该区域在轴向方向深度很小,从而激发出一个存在于表面附近的超声波力源。图5为不同激光能量辐射中心处的温度变化。光斑半径均为600 μm,脉冲持续时间均为10 ns。已知铝的熔点约为853~1 013 K,沸点约为2 740 K,当激光脉冲能量为100 mJ时,铝板表面温度已接近沸点,达到2 200 K,铝板表面造成损伤。结果表明:脉冲激光能量应控制在100 mJ以内,以保证功率密度低于材料的损伤阈值,从而避免对材料表面造成损伤。故后续模型均设定激光能量为10 mJ。
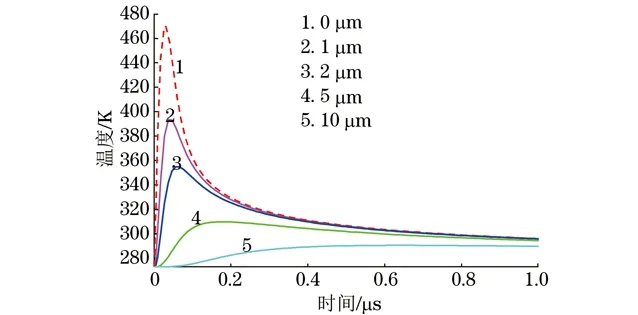
图4 激光辐射中心不同深度处温度随时间变化的关系
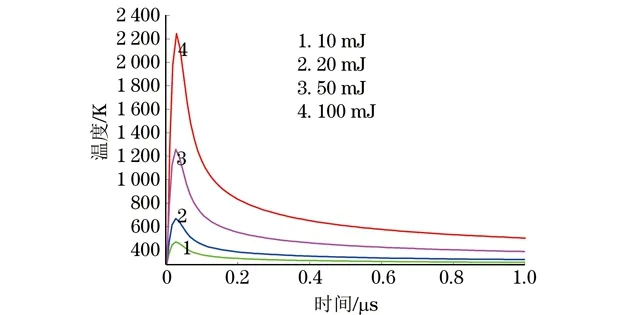
图5 不同激光能量辐射中心处的温度变化
2.3 位移场
脉冲激光形成瞬态温度场的梯度分布产生的热应力是超声波的激发力源,因此,精确的温度场计算是准确分析超声波产生过程的基础。由于应力自由的边界条件,材料的表面形成表面Rayleigh波,当材料厚度较小时,超声波在上下界面反射形成Lamb波。图6为0.2 mm厚的铝板中,距离激发源分别为5,8,10 mm处激光激发超声波的垂直位移。图7为0.8 mm厚的铝板中,距离激发源分别为5,8,10 mm处激光激发超声波的垂直位移。图8为10 mm厚的铝板中,距离激发源分别为20,25 mm处激光激发超声波的垂直位移。以上所有接收点全部位于材料上表面r轴向方向。

图6 0.2 mm厚的铝板中,离激光作用源不同距离处的超声波表面垂直位移
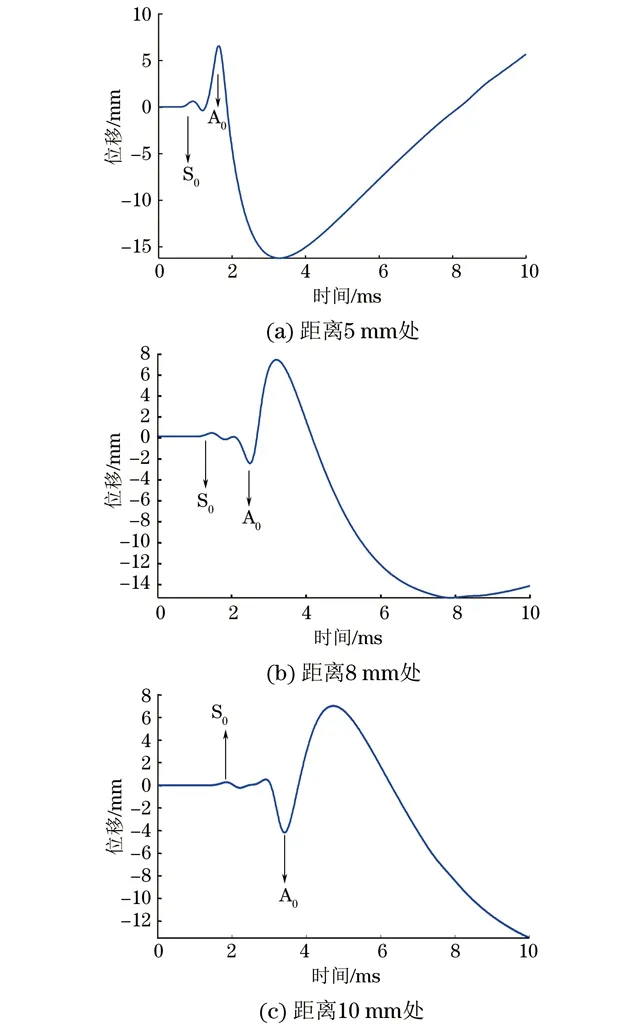
图7 0.8 mm厚的铝板中,离激光作用源不同距离处的超声波表面垂直位移
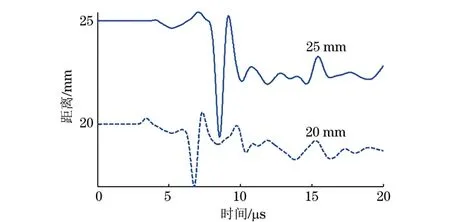
图8 10 mm厚的铝板中,激励接收距离分别为20,25 mm处的超声波表面垂直位移

图9 不同激光聚焦光斑半径下,激发得到Lamb波的时域特征和频域特征
激光脉冲的光斑半径也会影响激光激励超声波的特性,图9为激光聚焦光斑半径分别为0.6,0.4,0.2,0.1 mm时,在离光斑中心10 mm处接收到的Lamb波的时域特征和频域特征,材料厚度均为0.2 mm,激光脉冲能量均为10 mJ,脉冲持续时间均为10 ns。由图9(a)可以看出,随着光斑半径的减小,Lamb波峰值幅度逐渐增大,这是由于激光光斑半径的减小导致辐射区域功率密度增大,提高了激发Lamb波的能量。不同激光光斑半径激发的Lamb波最高频率和频带范围如表1所示,可看出,随着激光光斑半径的减小,所含的频谱成分越丰富,高频成分强度增大,频带越宽。这说明,为提高激光Lamb波的频率范围,可通过减小脉冲激光光斑半径来实现。
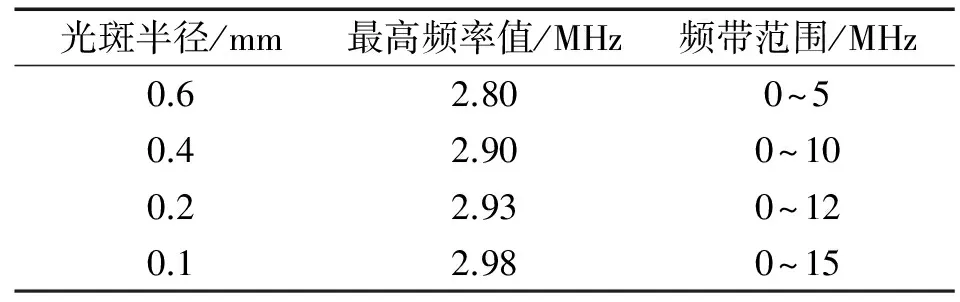
表1 不同激光聚焦半径激发的Lamb波最高频率和频带范围
3 位移场结果验证和分析
对图6(c)所示的0.2 mm厚铝板的有限元仿真结果,利用短时傅里叶变换做时频分析,结果如图10所示。可以看出,有限元分析得到的Lamb波的频率主要分布在0~2 MHz以内,在这个频段内,高阶模态不存在,因此图6(c)中只包含低阶S0和A0模态。
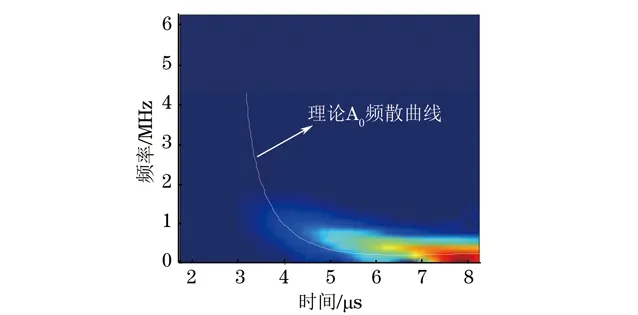
图10 0.2 mm厚铝板中,激励接收距离为10 mm的Lamb波信号
由0.2 mm厚铝板的频散曲线可知,频率范围在0~2 MHz时,S0模态的相速度几乎不随频率的变化而变化,频散现象不明显。而A0模态的频散曲线在该频率范围内显示出明显的频散特性。S0模态的群速度在该频段内基本不变,理论值约为5 433 m·s-1,当激励接收距离为10 mm,接收到S0模态的时刻在1.85 μs左右,对比图6(c)可以看出,约在1.9 μs可以观察到一个小波包。由于S0模态在该频段内主要以面内位移为主,垂直表面的位移相对较小,由此可以确定这个小波包为S0模态。图10中的时频图与理论的A0曲线相吻合,且在8 μs处能量最高,和图6(c)中8 μs时的信号幅值最大的结果相一致,由此可以确定图6(c)中第二个频散严重的波形为A0模态。从图6和图7可以看出,随着时间的推移,接收到的A0模态的波形逐渐变宽、幅值增大。这是因为在0~2 MHz的频段内,A0模态的波速和频率成正比,因此首先接收到高频的A0模态,然后才是低频的A0模态。激光点源激励出的Lamb波能量以低频占优,因此后面接收到的低频A0模态的幅值要比前面接收到的高频A0模态的幅值要高。
铝板厚度远大于超声波波长时,波形会向表面波Rayleigh波转化。
4 结论
(1) 通过有限元模拟出激光辐射在材料表面的瞬态温度场分布、超声波的传播过程,揭示了激光激发Lamb波的机理。分析了温度场,为脉冲激光能量的选取提供了依据,说明了功率密度低于材料的损伤阈值时,可避免对材料造成损伤。
(2) 铝板的厚度影响激光激励的Lamb波特征。当材料较薄时,激光点源激励出的超声波以低阶Lamb波为主,且低频成分的Lamb波能量占优。材料厚度远大于超声波波长时,波形会向表面波Rayleigh波转化。
(3) 脉冲激光的光斑半径也影响超声Lamb波的特征。随着半径的减小,Lamb波信号幅值变大,激发效率提高,且所含的频谱成分越丰富,频带越宽。
[1] 张淑仪.激光超声与材料无损评价[J].应用声学,1992, 11(4): 1-6.
[2] 何存富. 激光超声技术及其应用研究[D].北京:清华大学, 1995.
[3] 周正干,孙广开,李征,等. 复合材料层压板钻孔分层激光超声检测方法[J]. 机械工程学报, 2013,49(22): 29-33.
[4] CAUTO A, MARTARELLI M, PANDARESE G, et al. Experimental investigation by laser ultrasonics for high speed train axle diagnostics[J]. Ultrasonics, 2015, 55(1): 48-57.
[5] WU L, CHEN J C, ZHANG S Y. Mechanisms of laser-generated ultrasound in plates[J]. Journal of Physics D:Applied Physics,1995,57(18):1882-1884.
[6] WU L, CHEN J C, ZHANG S Y. Laser-generated transient Lamb wave in thin plates[J]. Chinese Physics Letters, 1996, 13(1): 24-27.
[7] SPICER J B, MCKIE A D W, WAGNER J W. Quantitative theory for laser ultrasonic waves in a thin plate[J]. Applied Physics Letters, 1990, 57(18): 1882-1884.
[8] LEE J H, Burger C P. Finite element modeling of laser-generated Lamb waves[J]. Computers & Structures, 1995, 54(3): 499-514.
[9] 许伯强,倪晓武,沈中华,等. 激光激发板状材料中超声导波的有限元数值模拟[J]. 中国激光, 2004, 31(5): 621-625.
[10] 许伯强,王纪俊,王国余,等. 金属材料中激光产生Lamb波的数值模拟[J]. 江苏大学学报(自然科学版),2005, 26(6): 542-546.
[11] 孙宏祥,许伯强. 激光激发Lamb波的有限元时域和频域数值分析[J]. 中国激光, 2010, 37(2): 537-542.
[12] 关建飞,沈中华,许伯强,等. 板状材料中脉冲激光激发超声导波的数值分析[J]. 光电子·激光, 2005,16(2): 231-235.
[13] SCRUBY C B, DRAIN L E. Laser ultrasonics:techniques and applications[M]. Bristol: Adam Hilger, 1990.
[14] ACHENBACH J D. Laser excitation of surface wave motion[J]. Journal of the Mechanics and Physics of Solids, 2003, 51(11/12): 1885-1902.
[15] XU B, SHEN Z, NI X, et al. Numerical simulation of laser-generated ultrasound by the finite element method[J]. Journal of Applied Physics, 2004, 95(4): 2116-2122.
Multi-parameter Numerical Simulation of Lamb Waves Induced by Laser in Aluminium Plates
LIU Zenghua, CAO Lihua, FENG Xuejian, HE Cunfu, WU Bin
(College of Mechanical Engineering and Applied Electronics Technology, Beijing University of Technology,Beijing 100124, China)
The effects of the parameters of laser and aluminium plate on laser-induced Lamb waves in aluminium plates are analyzed by using finite element method. Through the establishment of axis-symmetry laser radiation model, transient temperature field distribution under different laser energy is calculated. Research results show that surface material will be damaged when the laser energy is too high. Therefore, laser energy should be controlled to be lower than material damage threshold value. While laser energy is fixed, plate thickness and laser beam radius are changed, it is found that excitation rate of Lamb waves increases and signal spectra band broadens and spectral component becomes richer when laser beam radius decreases.
laser; finite element; Lamb wave; spectrum; aluminium plate
2016-08-15
国家自然科学基金资助项目(51475012, 11272021);北京市属高等学校高层次人才引进与培养计划资助项目(CIT& TCD201304048)
刘增华(1973-),男,教授,博士生导师,主要从事超声和电磁无损检测技术、结构健康监测及传感器测试技术方面的研究工作
刘增华,liuzenghua@bjut.edu.cn
10.11973/wsjc201707003
TB551;TG115.28
A
1000-6656(2017)07-0012-06

