Interactions of ion acoustic multi-soliton and rogue wave with Bohm quantum potential in degenerate plasma

M S Alam,M G Hafez,M R Talukder,and M Hossain Ali

1 Department of Applied Mathematics,University of Rajshahi,Rajshahi-6205,Bangladesh

2 Plasma Science and Technology Lab,Department of Applied Physics and Electronic Engineering,University of Rajshahi,Rajshahi-6205,Bangladesh

3 Department of Mathematics,Chittagong University of Engineering and Technology,Chittagong-4349,Bangladesh

Interactions of ion acoustic multi-soliton and rogue wave with Bohm quantum potential in degenerate plasma

M S Alam1,3,†,M G Hafez1,3,‡,M R Talukder2,and M Hossain Ali1

1 Department of Applied Mathematics,University of Rajshahi,Rajshahi-6205,Bangladesh

2 Plasma Science and Technology Lab,Department of Applied Physics and Electronic Engineering,University of Rajshahi,Rajshahi-6205,Bangladesh

3 Department of Mathematics,Chittagong University of Engineering and Technology,Chittagong-4349,Bangladesh

This work investigates the interactions among solitons and their consequences in the production of rogue waves in an unmagnetized plasmas composing non-relativistic as well as relativistic degenerate electrons and positrons,and inertial non-relativistic helium ions.The extended Poincaré–Lighthill–Kuo(PLK)method is employed to derive the two-sided Korteweg–de Vries(KdV)equations with their corresponding phase shifts.The nonlinear Schrödinger equation(NLSE)is obtained from the modified KdV(mKdV)equation,which allows one to study the properties of the rogue waves.It is found that the Fermi temperature and quantum mechanical effects become pronounced due to the quantum diffraction of electrons and positrons in the plasmas.The densities and temperatures of the helium ions,degenerate electrons and positrons,and quantum parameters strongly modify the electrostatic ion acoustic resonances and their corresponding phase shifts due to the interactions among solitons and produce rogue waves in the plasma.

wave-wave interaction,rogue waves,degenerate plasmas,Bohm potential

1.Introduction

It is well known that the dense electron–positron–ion (epi)plasmas are prevailed in the astrophysical environments, such as in white dwarfs,neutron stars,and active galactic nuclei,[1–4]and are produced in the laboratory,such as in the intense laser–solid interaction experiments.[5,6]The relativistic or quantum effect becomes prominent due to the fact that the interelectron distance is comparable to the thermal de Broglie wavelength[1]in such high density(of the order of 1030cm−3)plasmas,e.g.,in white dwarfs.In such extremely high density plasmas,the electron thermal energy is much less the electron Fermi energy.According to Pauli’s exclusion principle,the electron thermal pressure can thus be neglected[7]compared to the Fermi degeneracy pressure. The astrophysical objects sustain against the enormous gravitational forces due to the extremely dense degenerate electron pressure.In such case,the tunneling of the plasma species associated with the Bohm potential and statistical Fermi–Dirac pressure plays a significant role[8]on the structures and dynamics of the ion acoustic(IA)waves as observed in different astrophysical and space plasmas,[9,10]such as in white dwarf[1]and magnetars.[11]

[4]and[12]–[21]have investigated the structures and nonlinear propagation of IA waves considering either degenerate or non-degenerate plasmas.Mamun and Shukla[12]investigated the structures of the shock waves(SWs)in degenerate dense plasma in order to explain the phenomenon observed in white dwarfs.Rah man et al.[17]showed that the positron concentration and the relativistic plasma parameters significantly modify the amplitude,width,and phase velocity of the IA waves in epi plasmas.Haas et al.[18]found that the interaction of plasma particles with the Bohm potential significantly affects the properties of the nonlinear IA waves. Bhowmik et al.[19]studied the effects of quantum diffraction parameter(H)and equilibrium plasma species density ratio on the propagation of electron acoustic waves in the quantum plasmas.Recently,Hossen et al.[8]considered a degenerate epi plasma system consisting of inertial non-relativistic light ions,degenerate electrons,and positrons and noted the effects of tunneling of the plasma particles with the Bohm potentialon the propagation of IA waves by deriving the KdV,mKdV,and mixed mKdV(mmKdV)equations.On the other hand,many authors[22–29]have studied the propagation phenomena of the rogue waves by transforming the KdV,mKdV,and mmKdV equations to the corresponding NLS equations.Besides,Mandal et al.[30]have investigated only the overtaking collisions and phase shifts of dust acoustic multi-solitions in a four component dusty plasma.However,the interactions between single-and multi-solitons and hence the production of rogue waves along with their structures and dynamics are still unrevealed in the plasmas[8]for better understanding the physical issues observed in space plasmas.[25–29,31–38]Being motivated, for the significance of the problems related to the astrophysical and laboratory plasmas,we study the interaction processesof the IA single-,and multi-solitons,and their phase shifts as well as rogue waves in an unmagnetized plasmas composing degenerate electrons and positrons including Bohm quantum potential and an inertial non-relativistic light ions.The effects of helium ion mass and density,degenerate electrons, and positrons densities and temperatures on the phase shift, interactions among the IA single-and multi-solitons,and the production of rogue waves are investigated.

The paper is organized as follows.The theoretical model and derivations of two-sided KdV equations are presented in Section 2.The single and multi-solitons solutions of the KdV equations and their corresponding phase shifts are illustrated in Section 3.Derivation of nonlinear Schrödinger equation (NLSE)along with the solution of its rational function is displayed in Section 4.The results and discussion are described in Section 5.Finally,the conclusion is drawn in Section 6.

2.Governing equations

2.1.Model equations

The electrons(positrons)remain non-relativistic if their Fermi energy is less than their rest mass energy[39]in high density plasmas.On the other hand,the electrons have Fermi energy that is comparable to or greater than their rest mass energy,and hence the electron Fermi speed turns out to be comparable to the speed of light in vacuum for the number densities in the range of 1029–1034cm−3.Chandrasekhar[4,40]explained the equation of state for degenerate plasmas,as observed in an astrophysical compact object,namely,white dwarf,considering degenerate pressure exerted by plasma fluid aswhere α=5/3,(Λc=π¯h/msc=1.2×10−10cm,¯h=h/2π)for the nonrelativistic and γ=4/3,Ks≈(3/4)¯hc for the ultra-relativistic cases,msand nsare the plasma species mass and density,and h and c are the Planck constant and velocity of light in free space,respectively.In this report,an unmagnetized dense epi plasma system is considered composing both non-relativistic and relativistic degenerate electrons and positrons,and inertial non-relativistic light ions.ne0=np0+ni0is considered as the quasi-neutrality condition,where ne0,np0,and ni0are the densities of the unperturbed electrons,positrons,and ions,respectively.To study the structures and dynamics of the IA waves including their electrostatic resonance phenomena,corresponding phase shifts,and production of rogue waves in the considered plasmas,the normalized fluid equations[8]can be written as

Here,ns(s=i,e,p)is normalized by their equilibrium counterparts ns0,uiis the ion fluid speed normalized by ion acoustic speed Ci=(kBTFe/mi)1/2,φ is the electrostatic potential normalized by(kBTFe/e),η1=(TFp/TFe),µ=(ne0/ni0), σ=(n p0/n i0),j=e,p,kBis the Boltzmann constant,miis the ion rest mass,and TFp(TFe)is the Fermi temperature of positron(electron).The time and space variables are normalized byrespectively. The remaining dimensionless quantum parameters are β(=and λwhereandintroduced in Eqs.(3)and(4)due to the tunneling effect associated with the Bohm potential.[41]

2.2.Derivation of two-sided KdV equations

The two-sided KdV equations are derived by employing the extended Poincaré–Lighthill–Kuo(PLK)method[38].According to the extended PLK method,the scaling variables x and t are defined as

and the perturbed quantities can be written as

where ξ and η indicate the trajectories between the IA waves that are propagating toward each other,Vpis the unknown phase velocity of the IA waves normalized by Ci,and ε is a small parameter.The unknown phase functions X0(η,τ)and Y0(ξ,τ)will be evaluated later.Substituting Eqs.(6)and(7) into Eqs.(1)–(5)and equating the quantities with the same orders of ε,one can obtain coupled equations.Taking the lowest order of ε gives the following equations:

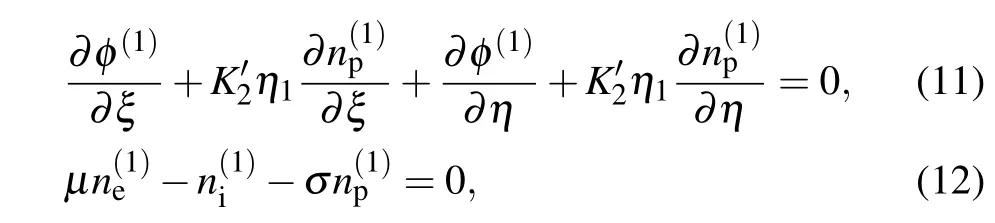
Equation(13)indicates the two-sided electrostatic waves,one of whichis propagating to the right direction from ξ=0, η→−∞to ξ=0,η→+∞and the otheris propagating to the left direction fromη=0,ξ→+∞to η=0,ξ→−∞. By inserting Eq.(13)into Eq.(12),the phase velocity is obtained as

Again,the next order of ε provides a set of equations in terms of the second order perturbed quantities,similar to Eqs.(8)– (12).One may also define the physical quantitiesandsimilar to those of Eq.(13).Considering the next higher order of ε yields a set of nonlinear evolution equations that are presented in Appendix A(Eqs.(A1)–(A5)).Simplifying Eqs.(A1)–(A5)with the help of Eq.(13)and then integrating with regards to ξ and η yield

It is clearly seen that the first and the second terms in the left hand side of Eq.(15)are proportional to η and ξ,respectively. Therefore,all the terms involved in the first two expressions of the left hand side of Eq.(15)become secular,which may be eliminated in order to stay away from resonances.[42]The following two-sided KdV equations are obtained to study the resonance phenomena of the electrostatic potential:

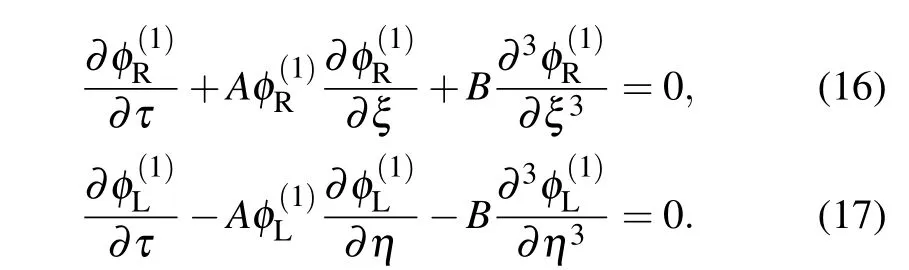
The third and the fourth terms of the left hand side of Eq.(15) may become secular terms in the next higher order and yield the following equations:

Equations(18)and(19)indicate that X0and Y0are the functions of η and ξ,respectively,which may be calculated with the help of analytical soliton solutions of KdV equations(16) and(17).

3.Soliton solutions and phase shifts

To study the nonlinear propagation characteristics of the interactions of the IAsolitons and their phase shifts in the plasmas,one has to derive the analytical soliton solutions of the KdV Eqs.(16)and(17)using the well established Hirota bilinear method.[43,44]According to this method,the single soliton solutions of Eqs.(16)and(17)can be obtained as

The trajectories of the solitary waves for weak interactions can be reduced to

To evaluate the phase shifts after interactions between the IA solitons,one may assume that the solitons,say R and L are asymptotically far away from each other at the initial time, that is,soliton R is at ξ=0,η→−∞and L is at η=0,ξ→+∞.After interaction,R is at ξ=0,η→+∞and L is at η=0,ξ→−∞to the right of L.The corresponding phase shifts are obtained as

Again,the double-soliton solutions of the KdV equations can be written as

and the corresponding phase shifts may be obtained due to the interactions of the double solitons as

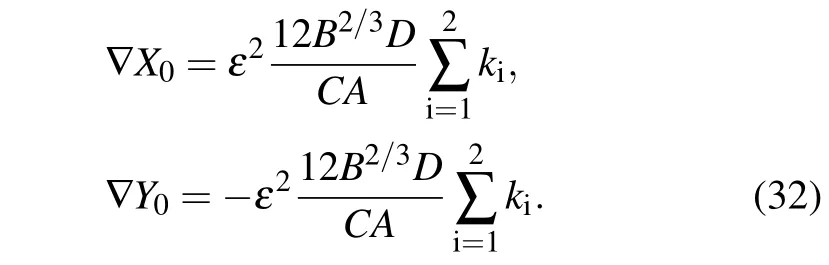
Finally,the triple-soliton solutions of the KdV equations can be written as

4.Derivation of NLSE with rogue wave solution

To study the behavior of weakly nonlinear wave packets in the plasmas,one can derive the NLSE considering the KdV equation as mentioned in Eq.(16).For simplicity,one can use the following equation for the transformation of variables:

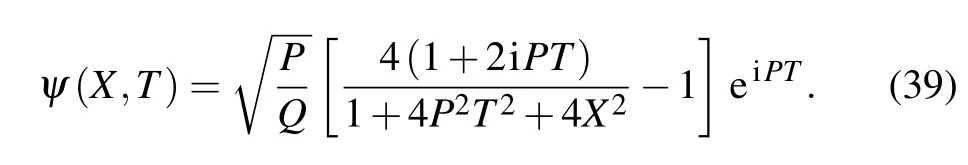
It is seen that the ratio of P and Q obtained is always negative, that is P/Q=−1/A2.Moreover,the weakly nonlinear theory predicts that quasi-monochromatic wave packets are always modulationally stable and the rogue waves cannot propagate due to the existence of the negative nonlinear coefficient terms in the NLSE.This indicates that the NLSE obtained from the KdV equation may not support the rogue wave solution.

On the other hand,there may arise the cases where the nonlinear coefficient(A)vanishes at the critical value (σc)for certain plasma parameters and equation(16)fails to study the nonlinear evolution of perturbation.For instance, A vanishes at σ=σc≈0.0195 for λ=0.10,β=0.10, γ=4/3,µ=0.1 and η1=0.8.In such a case,one can derive the mKdV equation by employing the stretched coordinates ξ=ε?x−Vpt?,τ=ε3t and perturbed quantities asinto Eqs.(1)–(5),whereandThe lowest power of ε gives the first order perturbed quantities asandThe next higher power of ε provides the second order perturbed quantitiesandthat are presented in Appendix A(Eqs.(A6)and(A7)). Finally,the next higher order of ε gives the following mKdV equation by taking the first and the second order perturbed quantities into account:[8]

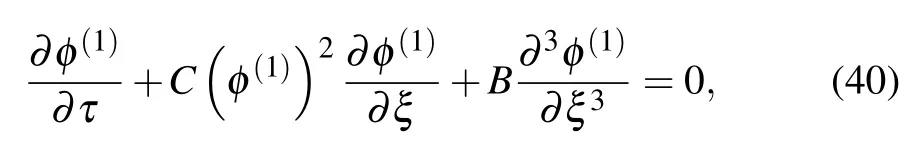
where

In order to obtain the rogue wave,substitute Eqs.(36)and(37) to the mKdV Eq.(40)and collect terms having the same order of ε.The lowest order approximation for m=1 with the first harmonic l=1 gives the dispersion relation of the electrostatic waves as ω=−Bk3.The second order approximation for m=2 with l=1 predicts vg=−3Bk2.Finally,the compatibility condition for the equation that is obtained from the next order(m=3,l=1)provides the NLSE as mentioned in Eq.(38).The nonlinearity(Q)and dispersive coefficients(P) are obtained as

5.Results and discussion

Two-sided KdV and NLSE equations are derived to investigate the unrevealed physical issues in the plasma considered, such as temporal evolution of electrostatic resonances and phase shifts due to the interaction of single and multi-solitons, and modulus instability.The effects of the plasma parameters on the temporal evolution of the electrostatic resonances, phase shifts,and rogue waves are investigated considering helium ion mass mi=6.68×10−24kg,ion density ni0=3.0× 1031cm−3,electron density ne0=9.11×1029cm−3,positron density np0=1.5×ne0,quantum parameters β=0.01–0.5 and λ=0.01–0.5 which are for the relativistic degenerate astrophysical plasmas.[4,12,45]The results obtained from this study are described below.

When two or more solitary waves propagate toward each other,they will interact and exchange their energies among themselves,and then separate off,regain their original wave forms.During the whole process of the interactions,the solitary waves are remarkably stable entities,preserving their identities through interaction.Each soliton gains two phase shifts,one is due to the head-on interaction and the other one is due to overtaking one soliton by the other one.On the other hand,the unique effect is due to the interactions that change their phase shifts.The phase shifts become either positive or negative due to head-on and overtaking interactions of the solitons,which is independent of the wave modes.[31–38]Figures 1(a)–1(f)illustrate the effects of σ and µ on the phase shift∇Y0due to the interaction among two,four, and six equal amplitude IA solitons in both ultra-relativistic and non-relativistic cases,respectively,taking the remaining parameters constant.It is seen that the changes of the phase shifts are decreasing with the increase of positron to ion density ratio σ=(np0/ni0).This means that with the increase of the positrons density,their interaction with electrons increases having opposite charges due to the contribution to the higher restoring forces.On the other hand,the changes of the phase shifts are increasing with the increase ofµ=(ne0/ni0)from 0.2 to 0.35 for ultra-relativistic and from 0.2 to 0.25 for nonrelativistic cases due to the interaction of oppositely propagating single and multi-solitons,and then decreasing significantly.It is provided that the electrons can contribute to the restoring force due to their small number density in the range 0.2≤µ≤0.35 and then the restoring force increases because the electrostatic interaction between electrons and positrons increases in the rangeµ＞0.35.Figures 2(a)–2(b)show the changes of phase shifts∇Y0with β for the interaction between equal amplitude single and multi-solitons in both cases,respectively,considering the fixed values of the remaining parameters.The quantum parameter β is mainly arisen due to the Bohm potential,which is solely responsible for the tunneling effect of the corresponding plasma components.It is clear from Fig.2 that the Bohm quantum potential significantly affects the phase shifts in which the changes of the phase shifts are decreasing with the increase of quantum parameter β.This phenomenon indicates that the electrons interact more actively with the helium ions,causing the reduction in the magnitude changes of the phase shift.Thus,it can be concluded that the phase shifts due to the interaction of two-sided single and multi-solitons are strongly dependent on the plasma parameters and the wave numbers.

Fig.1.(color online)Effects ofµand σ on the phase shift∇Y 0 due to the interaction between two((a)and(b)),four((c)and(d)),and six (1(e)and(f))equal amplitude IA solitons for non-relativistic helium light ions with α=5/3,ultra-relativistic(γ=4/3),and non-relativistic (γ=5/3)electrons and positrons,respectively,where η1=0.6,λ=0.1,β=0.1,k1=1,k2=2,k3=3 and ε=0.1.

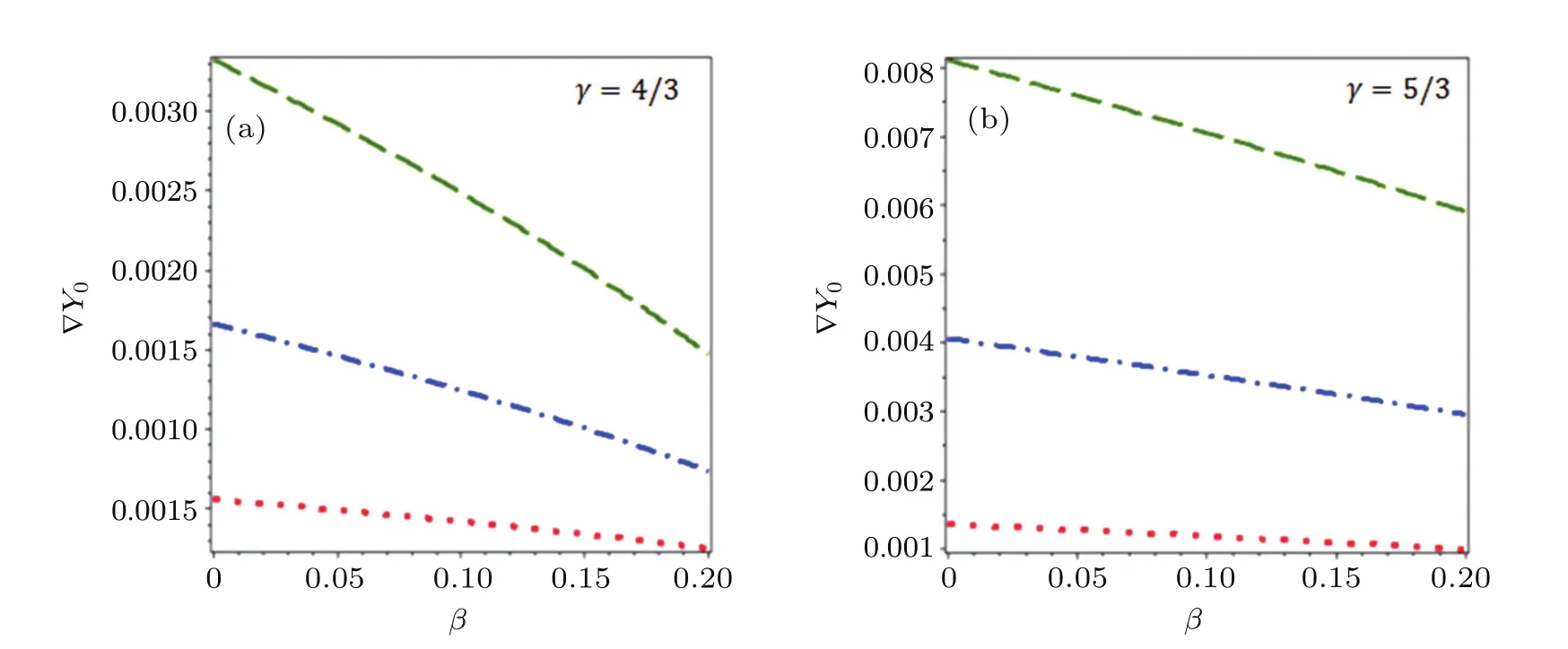
Fig.2.(color online)Effect of β on the phase shift∇Y 0 due to the interaction between two(red color),four(blue color),and six(green color) same amplitudes IA solitons for non-relativistic helium light ions with α=5/3)and ultra-relativistic(γ=4/3)as well as non-relativistic (γ=5/3)electrons and positrons,where η1=0.6,λ=0.1,µ=0.4,σ=0.6,k1=1,k2=2,k3=3,and ε=0.1.

Fig.3.(color online)Electrostatic potentialprofiles due to the interaction between equal amplitude single solitons at different τ and β with inertial non-relativistic helium ions for both ultrarelativistic(γ=4/3)and non-relativistic(γ=5/3)degenerate electrons and positrons,where η1=0.6,λ=0.10,µ=0.40,k1=1 and σ=0.5.

Figures 3(a)–3(d),4(a)–4(d),and 5(a)–5(d)display the two-sided equal amplitude electrostatic potential structuresfor single,double,and tripple-soliton against ξ and η,respectively,with different values of β and τ taking the remaining parameters constant for both ultrarelativistic and non-relativistic cases.It is seen from these figures that the amplitudes and widths of both right and left moving solitons are decreasing with increasing β.The quantum parameter β is mainly arisen due to the influence of the Bohm potential and exclusively related to the tunneling effect of the corresponding plasma component.The tunneling effect is also increasing with the increase of β.It is ensured that the electrons interact more actively with the ions,causing the reduction in amplitude and width of solitons,which is in agreement with the theoretical finding of Ref.[8].Furthermore,the potential profilesof the solitons are shifted towards the right,whileare shifted towards the left with increasing τ.This dictates that the position of solitons R is at ξ=0,η→−∞and that of L is at η=0,ξ→+∞before interaction and they collide at time t→0 and then the soliton R is at ξ=0,η→+∞and L is at η=0,ξ→−∞after interaction,such interaction phenomena are displayed in Figs.3–5.

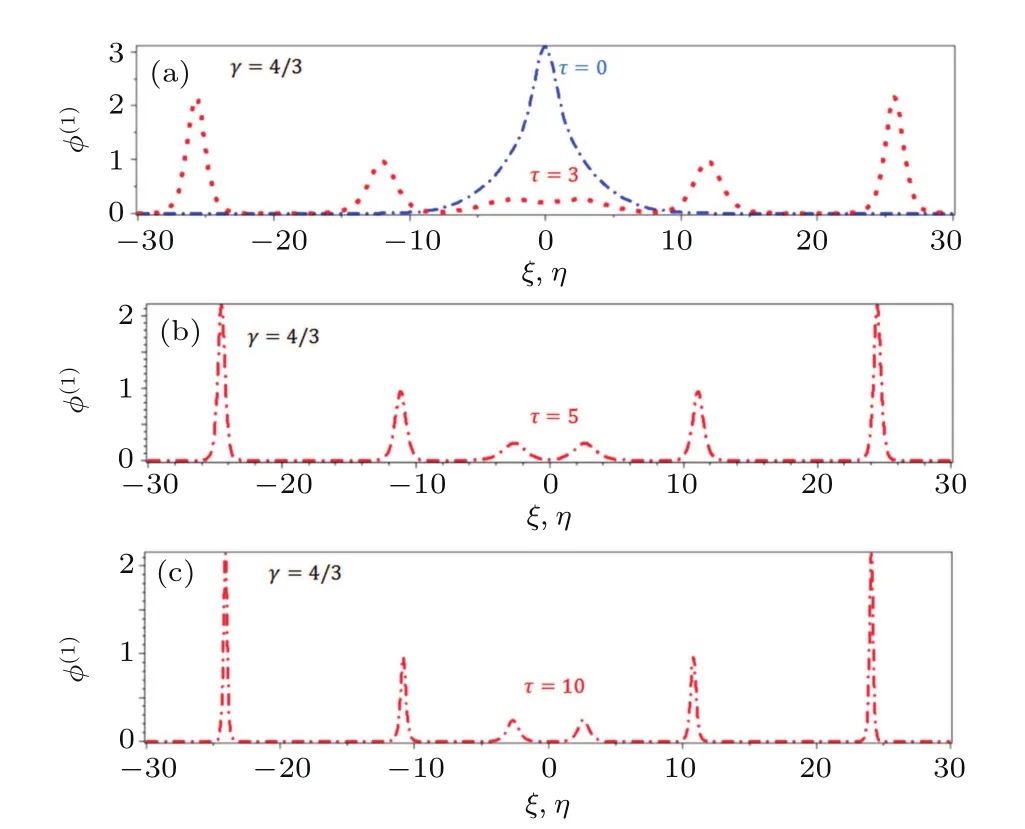
Fig.5.(color online)Electrostatic potential(φ(1))profiles due to the interaction between equal amplitude tripple solitons at different τ for ultra-relativistic(γ=4/3)degenerate electrons and positrons,and inertial non-relativistic helium ions,where η1=0.6,λ=0.10,β=0.10, µ=0.40,k1=1,k2=2,k3=3 and σ=0.5.

On the other hand,it is found that the NLSE obtained from the KdV equation does not support rogue wave solutions due to the modulational stability of the quasi-monochromatic wave packets.But,the NLSE obtained from the mKdV equation supports the rogue wave solutions for the considered plasma parameters as well as the critical value for which the nonlinear coefficient A of the KdV equation is zero.Figures 6(a)and 6(b)show the influences of σ and β on the rogue waves,respectively,taking different values of µ and remaining parameters constant for ultra-relativistic degenerate electrons and positrons.It is seen that the amplitudes of the rogue waves are decreasing with increasing β,σ andµin the plasmas.The quantum parameter β arises due to the Bohm potential which is solely responsible for the tunneling effect of the corresponding plasma component.The tunneling effect becomes pronounced with the increase of β,which dictates that the electrons interact more actively with the ions,causing the reduction of amplitude of rogue waves.Furthermore, the amplitude of the rogue waves decreases significantly due to the increase of σ and µ in the aforementioned plasma system,which predicts that the electrostatic interaction between electrons and positrons increases,and thus their contribution to the restoring force increases in the plasmas.Finally,figures 7(a)–7(d)display the existence regions(red color)of the rouge waves with repect toµ,β,σ,and η1along with k, respectively,taking the remaining parameters as constant for ultra-relativistic degenerate electrons and positrons.

Fig.6.(color online)Effect of(a)σ(β=0.10,T=0.01)and(b)β (σ=0.4,T=0.1)on the rogue waves for ultra-relativistic(γ=4/3) degenerate electrons,positrons,and inertialnon-relativistic helium ions, where the remaining parameters are η1=0.6,λ=0.10 andµ=0.40.

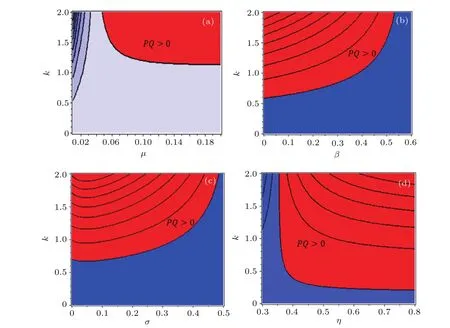
Fig.7.(color online)Contour plot of PQ for the existence regions(red color)of the rogue waves against(a)µand k(β=0.10,λ=0.10, η1=0.45,σ=0.01),(b)β and k(λ=0.10,η1=0.8,σ=0.3,µ=0.4),(c)σ and k(β=0.3,λ=0.3,η1=0.8,µ=0.1),and(d)η1and k (β=0.10,λ=0.10,µ=0.4,σ=0.3).

6.Summary

The interactions between the IA solitons,their phase shifts,and the production of rogue waves are investigated by considering the soliton solution of the two-sided KdV equations and the rational function solution of the NLSE,respectively.It is found that the quantum parameters become prominent due to the Bohm potential,which significantly modifies the propagation characteristics due to the interactions of the small amplitude long-lived solitons as well as large amplitude short-lived rogue waves in the plasmas.The results obtained in this study might be useful for the understanding of the effects of electrostatic resonance and phase shifts after weak interaction between multi-solitons and rogue waves for astrophysical compact objects,e.g.,white dwarfs,neutron stars,etc.,and for laboratory plasmas like intense laser–solid matter interaction experiments.

Appendix A

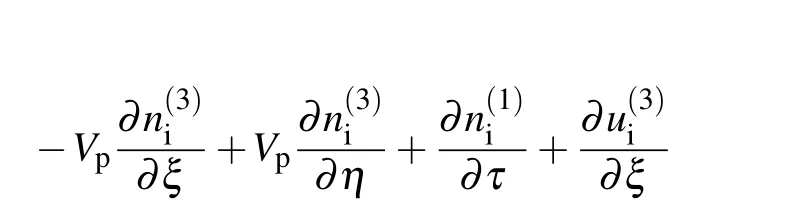
[1]Shapiro S L and Teukolsky S A 1983 Black Holes,White Dwarfs and Neutron Stars:The Physics of Compact Objects(New York:John Wileyamp;Sons)

[2]Garcia-Berro E,Torres S,Althaus L G,Renedo I,Lorn-Aguiltar P,Crsico A H,Rohrmann R D,Salaris M and Isern J 2010 Nature 465 194

[3]Woolsey N C,Courtois C and Dendy R O 2004 Plasma Phys.Control. Fusion 46 B397

[4]Mamun A A and Shukla P K 2010 Phys.Lett.A 374 4238

[5]Murklund M and Shukla P K 2006 Rev.Mod.Phys.78 591

[6]Berezhiani V I,Tskhakaya D D and Shukla P K 1992 Phys.Rev.A 46 6608

[7]Ata-ur-Rahman,Kerr M M,El-Taibany W F,Kourakis I and Qamar A 2015 Phys Plasmas 22 022305

[8]Hasan M M,Hossen M A,Rafat A and Mamun A A 2016 Chin.Phys. B 25 105203

[9]El-Bedwehy N and Moslem W M 2011 Astrophys.Space Sci.335 435

[10]Shatashvili N,Javakhishvili J and Kaya H 1997 Astrophys.Space Sci. 250 109

[11]Opher M,Silva L O,Dauger D,Decyk V K and Dawson J M 2001 Phys.Plasmas 8 2454

[12]Mamun A A,and Shukla P K 2010 Phys.Plasmas 17 104504

[13]Popel S I,Vladimirov S V and Shukla P K 1995 Phys.Plasmas 2 716

[14]El-Taibany W F and Tribeche M 2012 Phys.Plasmas 19 024507

[15]Shahmansouri M and Tribeche M 2014 Astrophys.Space Sci.349 781

[16]Hossen M A and Mamun A A 2015 Phys.Plasmas 22 102710

[17]Ata-ur-Rahman,Ali S,Mushtaq A and Qamar A 2013 J.Plasma Phys. 79 817

[18]Haas F,Garcia L G,Goedert J and Manfredi G 2003 Phys.Plasmas 10 3858

[19]Bhowmik C,Misra A P and Shukla P K 2007 Phys.Plasmas 14 12210

[20]Hafez M G,Talukder M R and Ali M H 2016 Waves in Random and Complex Media 26 68

[21]Hafez M G,Sakthivel R and Talukder M R 2015 Chinese J.Phys.53 120901

[22]Ruderman M S,Talipova T and Pelinovsky E 2008 J.Plasma Phys.74 639

[23]Rudermana M S 2010 Eur.Phys.J.Special Topics 185 57

[24]Grimshaw R,Pelinovsky D,Pelinonsky E and Talipova T 2001 Physica D 159 35

[25]El-Tantawy S A and Moslem W M 2014 Phys.Plasmas 21 052112

[26]El-Tantawy S A,Wazwaz A M and Schlickeiser R 2015 Plasma Phys. Control.Fusion 57 125012

[27]El-Tantawy S A,El-Awady E I and Tribeche M 2015 Phys.Plasmas 22 113705

[28]El-Tantawy S A,El-Awady E I and Schlickeiser R 2015 Astrophys. Space Sci.360 49

[29]El-Tantawy S A 2016 Astrophys.Space Sci.361 164

[30]Mandal G,Roy K,Paul A,Saha A and Chatterjee P 2015 Z.Naturforsch.70 703

[31]Ghosh U N,Roy K and Chatterjee P 2011 Phys.Plasmas 18 103703

[32]Parveen S,Mahmood S,Adnan M and Qamar A 2016 Phys.Plasmas 23 092122

[33]Roy K,Ghorui M K,Chatterjee P and Tribeche M 2016 Commun. Theor.Phys.65 237

[34]Han J N,Li S C,Yang X X and Duan W S 2008 Eur.Phys.J.D 47 197

[35]Han J N,Du S L and Duan W S 2008 Phys.Plasmas 15 112104

[36]El-Labany S K,El-Shamy E F,Sabry R and Shokry M 2010 Astrophys. Space Sci.325 201

[37]Saha A and Chatterjee P 2014 Astrophys.Space Sci.353 169

[38]Xue J K 2004 Phys.Rev.E 69 016403

[39]Sadiq S,Mahmood S,Haque Q and Ali M Z 2014 The Astrophysical J. 793 27

[40]Chandrasekhar S 1935 Mon.Not.R.Astron.Soc.170 405

[41]Hossen M A and Mamun A A 2015 Phys.Plasmas 22 073505

[42]Chatterjee P,Ghosh U N,Roy K,Muniandy S V,Wong C S and Sahu B 2010 Phys.Plasmas 17 122314

[43]Hirota R 2004 The Direct Method in The Soliton Theory(Cambridge: Cambridge University Press)

[44]Alam M S,Hafez M G,Talukder M R and Ali M H 2016 arXiv:1611.10225

[45]Koester D and Chanmugam G 1990 Rep.Prog.Phys.53 837

25 March 2017;revised manuscript

18 June 2017;published online 24 July 2017)

10.1088/1674-1056/26/9/095203

†Corresponding author.E-mail:alam21nov 2016@yahoo.com

‡Corresponding author.E-mail:golam hafez@yahoo.com

©2017 Chinese Physical Society and IOP Publishing Ltd http://iopscience.iop.org/cpb http://cpb.iphy.ac.cn