Super-resolution and super-sensitivity of entangled squeezed vacuum state using optimal detection strategy

Jiandong Zhang(张建东),Zijing Zhang(张子静),†,Longzhu Cen(岑龙柱), Shuo Li(李硕),Yuan Zhao(赵远),‡,and Feng Wang(王峰)

1 Harbin Institute of Technology,Harbin 150001,China

2 Tianjin Jinhang Institute of Technology,Tianjin 300192,China

Super-resolution and super-sensitivity of entangled squeezed vacuum state using optimal detection strategy

Jiandong Zhang(张建东)1,Zijing Zhang(张子静)1,†,Longzhu Cen(岑龙柱)1, Shuo Li(李硕)1,Yuan Zhao(赵远)1,‡,and Feng Wang(王峰)2

1 Harbin Institute of Technology,Harbin 150001,China

2 Tianjin Jinhang Institute of Technology,Tianjin 300192,China

Interference metrology is a method for achieving high precision detection by phase estimation.The phase sensitivity of a traditional interferometer is subject to the standard quantum limit,while its resolution is constrained by the Rayleigh diffraction limit.The resolution and sensitivity of phase measurement can be enhanced by using quantum metrology.We propose a quantum interference metrology scheme using the entangled squeezed vacuum state,which is obtained using the magic beam splitter,expressed assuch as the N00N state.We derive the phase sensitivity and the resolution of the system with Z detection,project detection,and parity detection.By simulation and analysis,we determine that parity detection is an optimal detection method,which can break through the Rayleigh diffraction limit and the standard quantum limit.

entangled squeezed vacuum state,quantum metrology,parity detection

1.Introduction

Since laser was invented,interference metrology has been extensively applied in the field of precision measurement. However,phase sensitivity is restricted by the standard quantum limit.[1]Simultaneously,the resolution is similarly constrained by the Rayleigh diffraction limit.Quantum metrology can break through the limit,thereby becoming the focus of research.In the study of Lloyd et al.,it was shown that by exploiting the quantum states of light,it is probable to overcome the Rayleigh diffraction limit[2,3](super-resolution)and the standard quantum limit[4,5](super-sensitivity).Briefly,a series of quantum interference metrology schemes have been proposed.[6–8]Among them,the performance of the N00N state and squeezed vacuum state are relatively outstanding. The research team of Louisiana State University indicated that the sensitivity of the system could be increased fromto 1/N using the N00N state.[9]James Smith from the United States Naval Research Laboratory developed an adaptive optics correction method for the N00N state.[10]The use of the squeezed vacuum state injection to reduce the noise was verified by the research team at Northwestern University.[11]Investigations from Louisiana State University research team revealed that super-sensitivity can be achieved by using a two mode squeezed vacuum state.[12]In this paper,we establish a quantum metrology model using the entangled squeezed vacuum(ESV)state.We will also describe the phase sensitivity and the resolution with Z detection,project detection,and parity detection.By calculating the phase sensitivity and resolution,an optimal detection method is discovered,which exhibits super-resolution and super-sensitivity.Finally,the influence factors of signal resolution and phase sensitivity are analyzed.

The ESV state interference measurement device is shown in Fig.1.It is similar to a Mach–Zehnder interferometer.The upper part is mode A,and the lower part is mode B.When the input state on port A is a squeezed vacuum state,|ξ〉A= SA(ξ)|0〉A,with ξ=r eiθ.Moreover,portBis a vacuum state |0〉B.The input state can be written as|ψin〉=|ξ〉A|0〉B.Then, the two modes quantum state passes through a magic beam splitter(MBS).[13]MBS possesses only two modes:complete transmission or full reflection.When the mode is complete transmission,the two modes quantum state exhibits mutual exchange.Therefore,the output state is|0〉A|ξ〉B.When the mode is full reflection,the two modes quantum state exhibits no exchange.The output state at this time is|ξ〉A|0〉B.With the total probability for the transmission and reflection being 1:1,the quantum state has become a highly entangled state |ψ1〉=K(|ξ〉A|0〉B+|0〉A|ξ〉B).It is called the ESV state. Here,is a normalized coefficient.With two pathways from the MBS to the beam splitter where the length difference of two optical paths is represented by the phase shift ϕ of mode B,[14]the quantum state is changed to

Fig.1.(color online)Quantum interference metrology scheme with entangled squeezed vacuum state.

2.Quantum detection strategy

2.1.Z detection

First,the zero–nonzero photon counting at the output port A is analyzed.The counting data{a,b}are grouped into binary outcomes:0 for a=0 and/0 for a/=0.[15,16]We expand the state|ψ2〉as

where

According to the transformation theory of the beam splitter, we obtain the output state

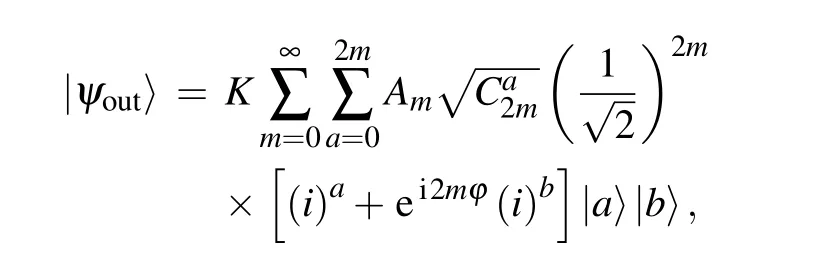
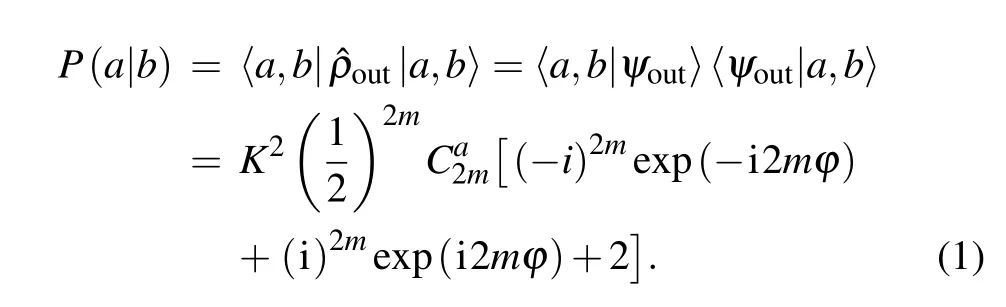
The probability of detecting zero photon on port A is

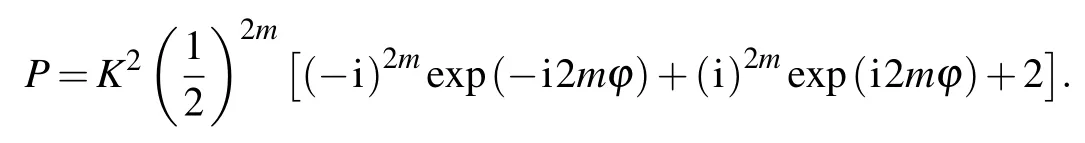
For different values of m,the probability changes periodically.

The reason for this result is that the power of the imaginary number i produces a circle every four times(in=in+4). The photon probability distribution for a squeezed vacuum state is oscillatory,thereby vanishing for all odd photon numbers.Therefore,the expression of the signal can be writtenwhere|Am|2is the probability of detecting 2m photons in the squeezed vacuum state.P2mis the probability of detecting zero photon on port A when the photon number in the squeezed vacuum state is 2m.Namely,

However,this is an infinite series summation.Therefore, it is difficult to obtain an analytical solution.We make some rules to truncate the sum.In other words,small probability series items are eliminated.When the total probability of the first m items is more than 99%or the probability of m th is less than 0.1%,the sum operation is stopped.This is analogous to the theory of“random walk.”[17]

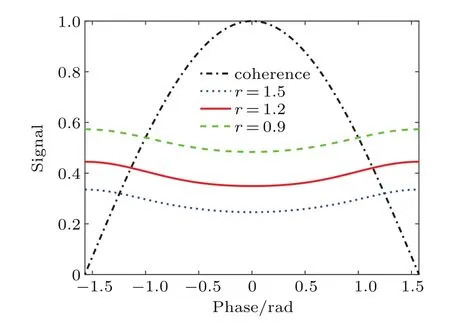
Fig.2.(color online)Variation of signal resolution with different squeezing parameters.

To clearly observe the behavior of the signal resolution for this strategy,in Fig.2,we plot the signal resolution as a function of phase.It can be observed from the figure that this method cannot achieve super-resolution and the visibility is low.The definition and the details of visibility can be found in Ref.[13].When the squeezing parameter increases,the visibility will increase,but the peak value of the signal will reduce.

This result can be perceived,because the counting data of Z detection are grouped into binary outcomes.When the value of 2m is larger,the binomial coefficient of P2mis smaller. That is,the possibility of zero photon appearing on port A is smaller.Therefore,the resolution is poor with the increase of the photon numbers.

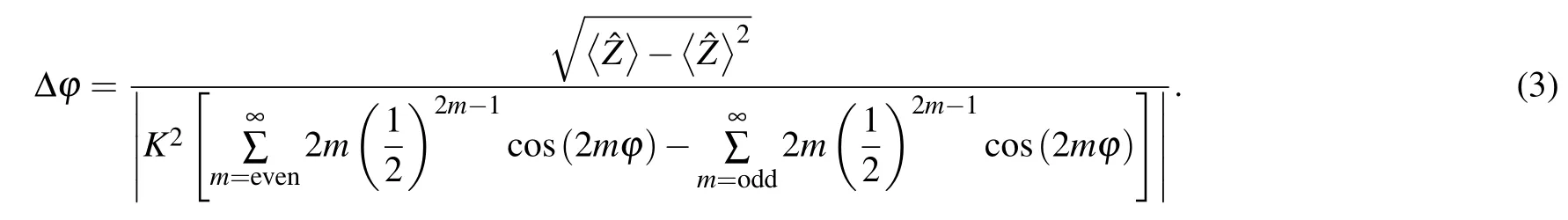
We determine that phase sensitivity cannot reach the standard quantum limit,and hence cannot achieve super sensitivity.

2.2.Project detection

Project detection is proposed by the Louisiana State University research team.[19]Then,this type of method is widely used in the field of quantum metrology.We expand the state |ψ2〉as

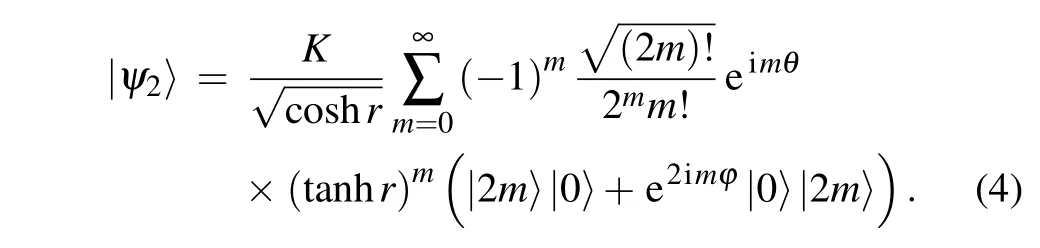
The phaseϕ can be determined by measuring the operatorthe expectation value of the operatoris

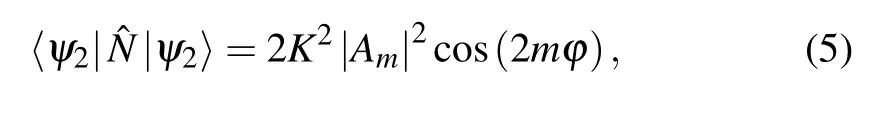
where

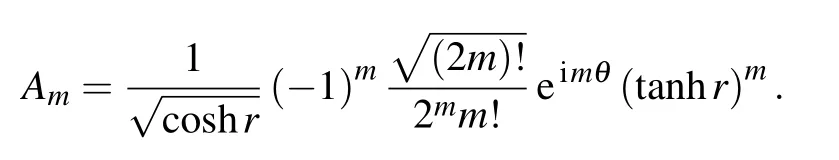
We consider two factors(m and r)and simulate the output signal.In Fig.3(a),m=1,the squeezing parameter r=0.3,0.6, and 0.9.It is not difficult to observe from the picture that the signal can achieve super-resolution;however,the visibility of the signal is low.With increase in the squeezing parameter,for the same m,the visibility of the signal increased.Figure 3(b) exhibits r=0.9,m=1,2,and 3.It can be observed from the figure that the super-resolution exhibits multiple peaks with increase in the value of m.However,the visibility decreases.According to the squeezing level of the squeezed vacuum state, we can select a suitable value of m to achieve super-resolution and ensure favorable visibility.

By using the error propagation,the phase sensitivity is given by

This strategy selects only one projector,|Am|2is small; hence,is also small.Therefore,the visibility of the signal is low.We consider projection onto all projectors.It has been demonstrated that the parity measurement on the output port A is equivalent to the measurement that is constructed from all projectors.[20]

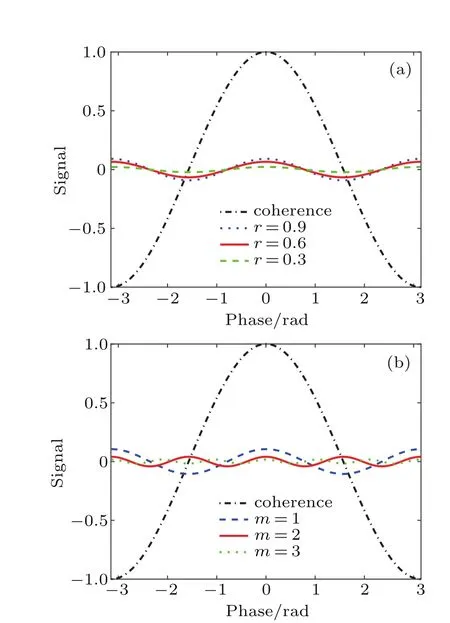
Fig.3.(color online)(a)Variation of signal resolution with different squeezing parameters.(b)Variation of signal resolution with different values of m.

Fig.4.(color online)Variation of sensitivity with different values of m.

2.3.Parity detection

Parity detection was originally discussed in the context of trapped ions by Bollinger etal.[21]and later adopted for optical interferometry by Gerry and Campos.There are several equivalent approaches of calculating the phase sensitivity.[22–24]The parity operator on output mode A iswhich divides the photon counting data{a,b}into binary outcomes±1.In other words,if a is an even number,The conditional probabilitiescan be obtained through a sum of Paover the odd or the even number of a.

Using the conclusions of the N00N state for parity detection,[25]the output signal of the system is

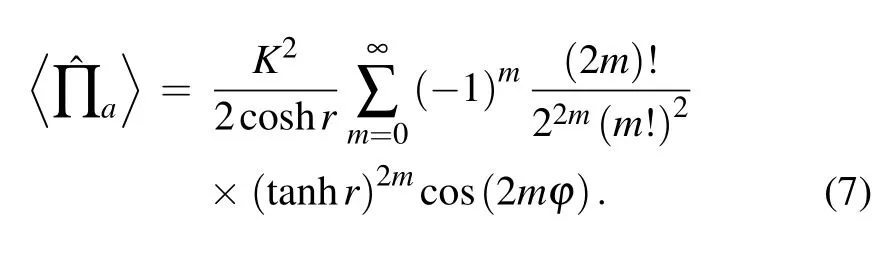
We also use the previously mentioned truncation method to obtain the output signal of the ESV state scheme.The results of the ESV state scheme are compared with the ones of the coherent state scheme when r=0.9,1.2,and 1.5(see Fig.5).We can observe that the peaks of the ESV state in Fig.4 are narrower than the coherent state input.This suggests that parity detection can achieve super-resolution.When the squeezing parameter increases,the peaks of the signal will become narrower,and the visibility will become bigger.For example,for r=0.9,visibility is about V=26.1%.Moreover,for r=1.5,the visibility is approximately V=51.9%. Furthermore,the visibility is approximately twice that of the visibility of r=0.9.

Here,we discuss two limit problems.The first is the threshold of the signal when achieving super-resolution.With the help of simulation analysis,we found that r=0.6 is the critical value of our scheme for achieving super-resolution. We can observe from Fig.5(b)that,when the squeezing parameter is less than 0.4,the signal peak is wide and it cannot break the Rayleigh diffraction limit.That is,the condition r＞0.4 should be satisfied to achieve super-resolution.

The second problem is the maximum visibility of the signal.As shown in Fig.5,the signal visibility is proportional to the squeezing parameter.Moreover,we draw the signal curve with large squeezing parameter to determine whether visibility will eventually tend to saturation.We found that the visibility of the signal can be saturated through simulation calculation.

Particularly,as shown in Fig.5(b),when the squeezing parameter is r=6,the resolution of the signal will reach 99%.Moreover,as the squeezing parameter increases,the signal peak width becomes narrow and finally tends to become a sharp peak similar to the delta function,and visibility is V=1. To be sure,in order to compare the width of the peak,we moved the coherent signal with parallel in Fig.5(b).

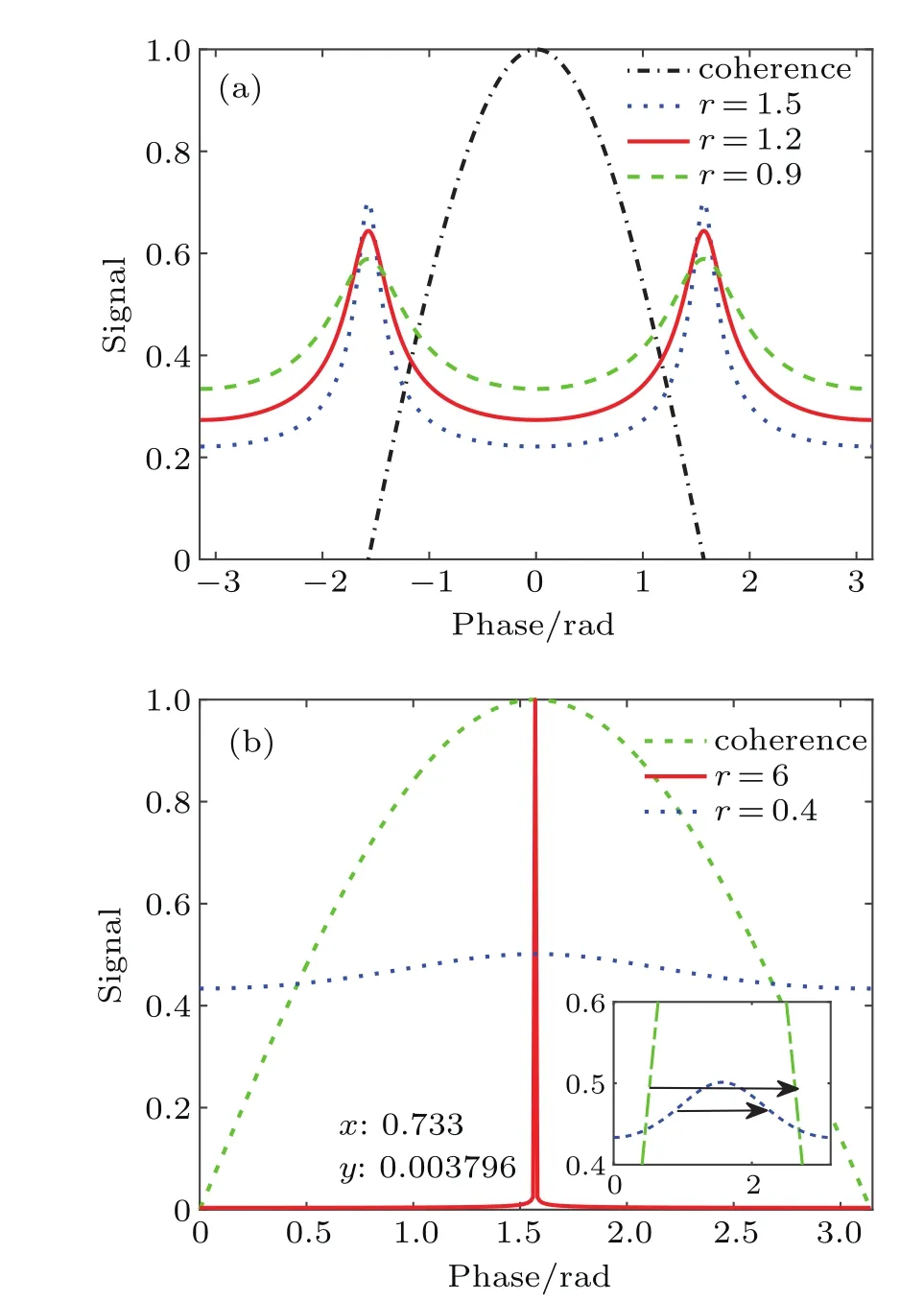
Fig.5.(color online)(a)Variation of signal resolution with different squeezing parameters.(b)Variation of signal resolution with critical condition.

The phase sensitivity can be estimated using the error propagation formula

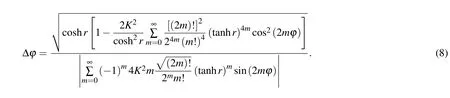
In Fig.6(a),we draw the curve of the sensitivity of the system with phase change(r=2)and the standard quantum limit.We can observe that the best sensitivity can break the standard quantum limit.It is presented in Fig.6(b)for the best sensitivity with the squeezing parameter from 0.9 to 2.5,and we also draw the standard quantum limit.The reason for selecting 0.9 is¯n=sinh2(0.9)≈1.It can be observed from the diagram,for r≥1.4,that the best sensitivity of the system can achieve super-sensitivity.

Our results are also verified for large squeezing parameters through simulation.For example,r=4,ΔϕSQL(4)= 0.03664 and ΔϕESV(4)=0.01538.In other words,in the case of large squeezing parameter,the ESV state scheme can still breakthrough the standard quantum limit and achieve super sensitivity.

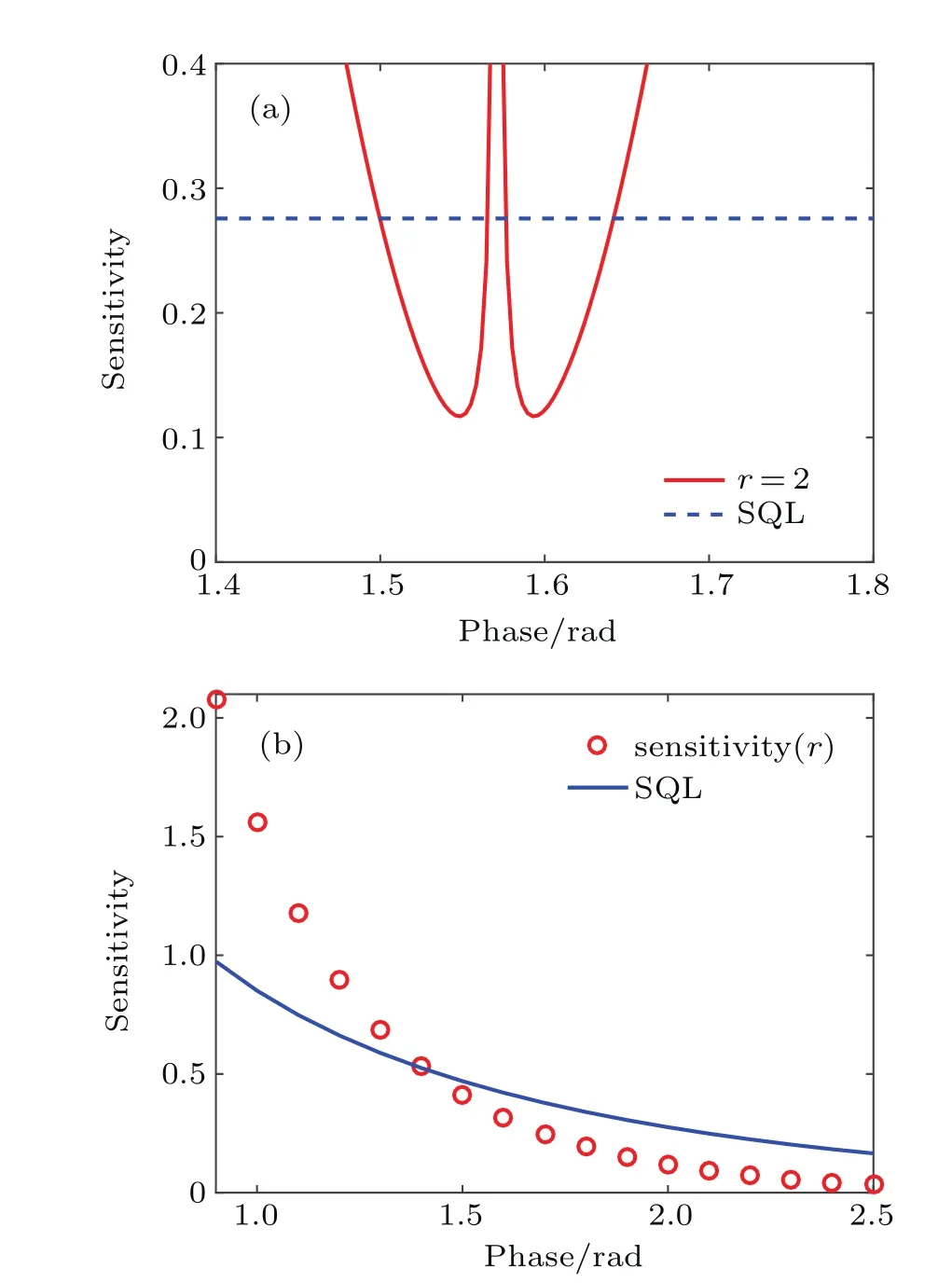
Fig.6.(color online)(a)Variation of phase sensitivity with r=2.(b) Best phase sensitivity from r=1.5 to r=2.5 and SQL.

Overall,the ESV state scheme can achieve super resolution and super-sensitivity,the super-resolution range is r＞0.4,the range of visibility reaches 1 when r＞6,and the super-sensitivity is established for r≥1.4.

3.Conclusion and perspectives

We present a quantum interference metrology scheme for the ESV state.Moreover,we derive the phase sensitivity and the resolution with Z detection,project detection,and parity detection.The final results reveal that Z detection cannot achieve super-sensitivity and super-resolution.This is because Z detection is to judge whether the output photon number is zero or nonzero.Project detection cannot achieve super sensitivity,but it can achieve super-resolution;the disadvantage is the visibility is low.The reason for this phenomenon is that project detection selects only one projector.Moreover,parity detection can achieve super-sensitivity and super resolution.This suggests that parity detection is more suitable for the ESV state scheme.The super-resolution range is achieved when r＞0.4.With the increase of squeezing parameter,the peak of the signal will become narrow,and the visibility of the signal will be enhanced.Therefore,the resolution will be promoted,and the range of visibility reaches 1 when r＞6.Super-sensitivity is established for r≥1.4. When the squeezing parameter increases,the sensitivity of the system will be enhanced.In addition,the squeezing parameter r=1.45 that corresponds to a squeezing of 12.6 dB was achieved under current experimental conditions.[26]This suggests that super-resolution and super-sensitivity will be obtained.With further perfect experimental conditions,our scheme will achieve better visibility of signal and sensitivity.

[1]Caves C M 1982 Phys.Rev.D 26 1817

[2]Shapiro J H and Lloyd S 2009 New J.Phys.11 063045.

[3]Cohen L,Istrati D,Dovrat L and Eisenberg H S 2014 Opt.Express 22 11945

[4]Lee H,Kok P and Dowling J P 2002 J.Mod.Opt.49 2325

[5]Giovannetti V,Lloyd S and Maccone L 2004 Science 306 1330

[6]Pooser R C and Pfister O 2004 Phys.Rev.A 69 043616

[7]Pezzé L and Smerzi A 2008 Phys.Rev.Lett.100 073601

[8]Xu X X 2015 Phys.Rev.A 92 012318

[9]Gerry C C and Mimih J 2010 Contemp.Phys.51 497

[10]Smith J F 2010 Proceedings of SPIE,April 13,2009,Orlando,United States,p.73420A

[11]Dutton Z,Shapiro J H and Guha S2010 J.Opt.Soc.Am.B 27 A63

[12]Anisimov P M,Raterman G M and Chiruvelli A 2010 Phys.Rev.Lett. 104 103602

[13]Dowling J P 2008 Contemp.Phys.49 125

[14]Zhang Y M,Li X W and Jin G R 2013 Chin.Phys.B 22 114206

[15]Escher B M and de Matos Filho R L 2011 Nat.Phys.7 406

[16]Escher B M,de Matos Filho R L and Davidovich L 2011 Braz.J.Phys. 41 229

[17]Li M,Zhang Y S and Guo G C 2013 Chin.Phys.B 22 30310

[18]Helstrom C W 1969 J.Stat.Phys.1 231

[19]Boto A N,Kok P and Abrams D S 2000 Phys.Rev.Lett.85 2733

[20]Gao Y,Anisimov P M and Wildfeuer C F 2010 J.Opt.Soc.Am.B 27 A170

[21]Gerry C C 2000 Phys.Rev.A 61 043811

[22]Seshadreesan K P,Anisimov P M and Lee H P 2011 New J.Phys.13 083026

[23]Knysh S,Smelyanskiy V N and Durkin G A 2011 Phys.Rev.A 83 021804

[24]Feng X M,Jin G R and Yang W 2014 Phys.Rev.A 90 013807

[25]Chiruvelli A and Lee H 2011 J.Mod.Opt.58 945

[26]Vahlbruch H,Mehmet M and Chelkowski S 2008 Phys.Rev.Lett.100 033602

16 March 2017;revised manuscript

2 May 2017;published online 31 July 2017)

10.1088/1674-1056/26/9/094204

†Corresponding author.E-mail:zhangzijing@hit.edu.cn

‡Corresponding author.E-mail:zhaoyuan@hit.edu.cn

©2017 Chinese Physical Society and IOP Publishing Ltd http://iopscience.iop.org/cpb http://cpb.iphy.ac.cn