基于FDTD的隧道衬砌质量雷达检测正演模拟及其应用分析
张 杨, 肖国强, 周黎明, 余信江
(长江科学院 a.水利部岩土力学与工程重点实验室,b.工程安全与灾害防治研究所,武汉 430010)
基于FDTD的隧道衬砌质量雷达检测正演模拟及其应用分析
张 杨a, 肖国强a, 周黎明a, 余信江b
(长江科学院 a.水利部岩土力学与工程重点实验室,b.工程安全与灾害防治研究所,武汉 430010)
针对隧道衬砌可能出现的不同的地质病害,根据其介质电性特征,构建相应的地球物理模型,基于时域有限差分(FDTD)算法和完全匹配层(PML)的吸收边界条件,利用GprMax软件结合Matlab编程作探地雷达正演模拟。研究结果表明,不同密度的钢筋和钢拱架模型,在不同中心频率的天线的正演结果中,受到探地雷达分辨率地影响,反射信号同相轴的强弱和形态有所不同,不同的形状的脱空模型其相位、振幅、波形特征都各不相同。结合工程实例,雷达正演模拟与实测剖面结果的主要异常波形信号及钻孔揭示情况基本相符,说明探地雷达能有效地检测衬砌病害的类型、位置、构造走向等空间分布特征,验证了该正演方法的可行性,有助于更好地指导物探工作者对衬砌质量进行更精确地解释,准确发现衬砌的地质病害,确保隧道运营安全。
隧道衬砌质量检测; 探地雷达; 不同形状的质量缺陷体; 时域有限差分算法
0 引言
在我国,随着隧道建设在公路、铁路、水利水电等大型工程中地普及,隧道工程的质量安全越来越受到关注。隧道因其复杂的工程结构和特殊的功能要求,施工难度大,施工过程中影响因素多。调查发现,相当多的隧道容易出现衬砌施工质量问题。衬砌施工的主要病害包括:衬砌脱空、空隙、钢筋网变形、钢筋网缺失、回填层不密实等。病害会减弱衬砌的承压能力,影响隧道的稳定性,对隧道的正常运营带来安全隐患,并且会加大隧道的维护费用,缩短隧道的使用寿命[1]。探地雷达法以其高分辨率、快速高效、无损等特点,在隧道工程质量检测中被广泛应用[2]。
利用探地雷达法对隧道衬砌施工质量检测的关键在于对雷达成果图的解释,通过软件对原始数据进行时深转换、增益调整、去噪、偏移归位等处理后,可得到雷达剖面成果图,通过对图像的波形大小、相位变化、振幅强弱等信息的解释,可以得出相应的检测结果。但是,由于施工现场的复杂性和检测条件的局限性,在施工现场有通风机、照明灯、接触网、钢缆、钻机等障碍物和金属电磁干扰物,测线布置过程中常受到钢筋、铁丝、衬砌表面不平整的影响,导致检测条件不理想[3],对检测采集的信号造成严重干扰,解释结果的合理性和准确性依赖于物探工作人员长期的经验。因此,对雷达剖面图像中质量缺陷体的去伪存真地识别非常重要。
笔者在前人的研究基础上,针对衬砌施工存在的主要病害及其形态,分析正演模拟的探地雷达剖面结果,有助于更好地指导实际病害的探测工作。
1 探地雷达及FDTD正演原理
1.1 探地雷达原理
探地雷达(GPR)是一种用于探测地下介质分布的地球物理勘探技术,探地雷达运用于隧道衬砌施工质量检测,其原理是通过发射天线发射宽频短脉冲的电磁波信号到隧道衬砌内部,当遇到存在电性差异的介质如钢筋、衬砌脱空、混凝土与围岩分界面时形成反射电磁波,反射电磁波返回到地面通过接收天线接收,根据接收到的反射电磁波波形、振幅强度、双程走时等参数,便可推断掌子面前方目标体的电性性质、地质结构、空间位置及几何形态[4],从而达到对衬砌混凝土内部质量缺陷体探测的目的。
所有的电磁现象,在宏观尺度上,是由著名的Maxwell方程组描述。Maxwell方程组描述了电磁场各属性参数之间的相互关系,为分析探地雷达的探测原理和性能提供了理论基础。数学上,电场、磁场及其二者的关系可描述如下:
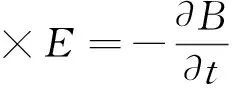
(1)
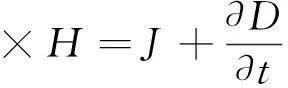
(2)
▽×D=q
(3)
▽×B=0
(4)
式中:E为电场强度矢量(V/m);q为电荷密度(C/m3);B为磁感应强度(T);J为电流密度(A/m2);D为电位移矢量(C/m2);t表示时间(s);H为磁场强度(A/m)。
1.2 FDTD正演原理
为了模拟探地雷达电磁波的波形在隧道空间中的传播情况,时域有限差分(FDTD)的原理是,选择雷达电磁波TM模式下在x,y平面上的传播,利用K S Yee网络模型,运用中心差商代替微商,将连续变量离散化。二维情形下Maxwell 方程的有限差分形式是:
(5)
(6)
(7)
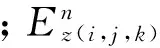
我们利用GprMax软件进行正演模拟,GprMax基本原理是基于美国学者K S Yee[5]通过引入Yee细胞提出的解Maxwell偏微分方程的方法,该方法基于时域有限差分算法(FDTD)和完全匹配层(PML)[6]的吸收边界条件。
完全匹配层(PML)吸收边界条件是一种媒质吸收型边界,其原理是构造了一种非物理的吸收媒质与FDTD网格外部相连,该吸收媒质的波阻抗与外向散射波的频率和入射角均无关[7-8]。
时域有限差分算法是有稳定条件的数值方法,稳定的条件称为CFL条件(Courant,Freidrichs和Lewy):
(8)
式中:c为光速;Δx和Δy分别为X方向和Y方向的空间步长;Δt为时间步长。
为了减少对网格步长数值引起的模型离散化的频率散射影响,需要满足以下的经验法则:
(9)
式中:Δl是网格步长;λ是介质的最小波长。
2 雷达正演模拟
2.1 应用条件
在隧道衬砌空间中,探地雷达发射的高频电磁波在介质中的传播速度取决于介电常数的大小。电磁波速与介质的相对介电常数的关系可用式(10)表示。
(10)
式中:C是光速。
电磁波在传播过程中,遇到不同的阻抗界面(介质分界面)时将产生反射波和透射波,其反射与透射遵循反射与透射定律,反射波能量大小取决于反射系数。电磁波在岩土介质分界面上的反射系数是与介质导电率、介电系数、导磁率及入射角度等有关。由于不同岩土介质之间导电率的差异可以达到几个数量级,因此,介质分界面两侧岩土介质的电磁波反射系数差异很大。
探地雷达高频电磁波在两种不同介质的分界面产生反射,电磁波反射系数的大小主要取决于反射界面两侧导电率的差异。表1给出了常规介质的典型参数[9]。
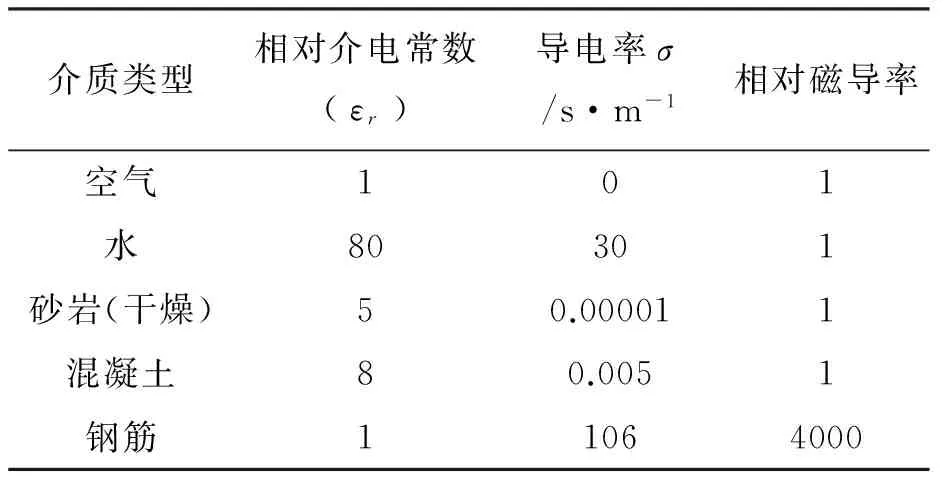
表1 常规介质电性参数Tab.1 Dielectric parameters of conventional media
2.2 隧道空间模型
隧道空间模型模拟实际隧道衬砌区域,设计一个4 m×0.8 m长方形,其中隧道衬砌混凝土对应x轴0 m~4 m,混凝土厚度范围对应y轴0 m~0.4 m,围岩范围对应y轴0.4 m~0.8 m。探地雷达正演对象为隧道衬砌从左至右0 m~4 m、深度0 m~0.8 m的范围。
2.3 钢筋和钢拱架正演模拟
在当今隧道施工工艺中,钢筋和钢拱架是隧道衬砌支护中一项重要内容,是隧道衬砌具有足够的承压强度的重要保障。但是由于施工过程中,偷工减料或者施工不标准,容易出现钢筋和钢拱架缺失、错段、变形等质量问题。
我们模拟了隧道衬砌空间下不同密度的钢筋和钢拱架模型(图1)。钢筋的直径为2 cm,埋设深度为15 cm。钢拱架长为20 cm、宽为10 cm,埋设深度为40 cm。设置三组不同密度的钢筋模型:第一组钢筋间距为8 cm;第二组钢筋间距为18 cm;第三组钢筋间距为38 cm。正演模拟参数分别用中心频率为500 MHz、800 MHz、1 200 MHz的天线进行正演模拟。模型区域为4 m×0.8 m,空间步长为Δx=Δy=0.000 1 m,时窗宽度为15 ns,天线采集道数为390。发射天线的初始位置为tx(0.05,0.05),接收天线的初始位置为rx(0.1,0.05),天线探测范围为从衬砌表面左端移动到右端。天线间距为0.05 m,道间距为0.01 m。混凝土、钢筋、砂岩的电性参数见表1。在混凝土介质中,雷达正演模拟的电磁波速度为0.12 m/ns。
将建立好的模型参数导入GprMax软件进行运算,再将得到的正演模拟数据导入自行编制的Matlab程序,经过时深转换、道间能量均衡等处理,可以绘制得到雷达正演剖面图(图2、图3、图4)。
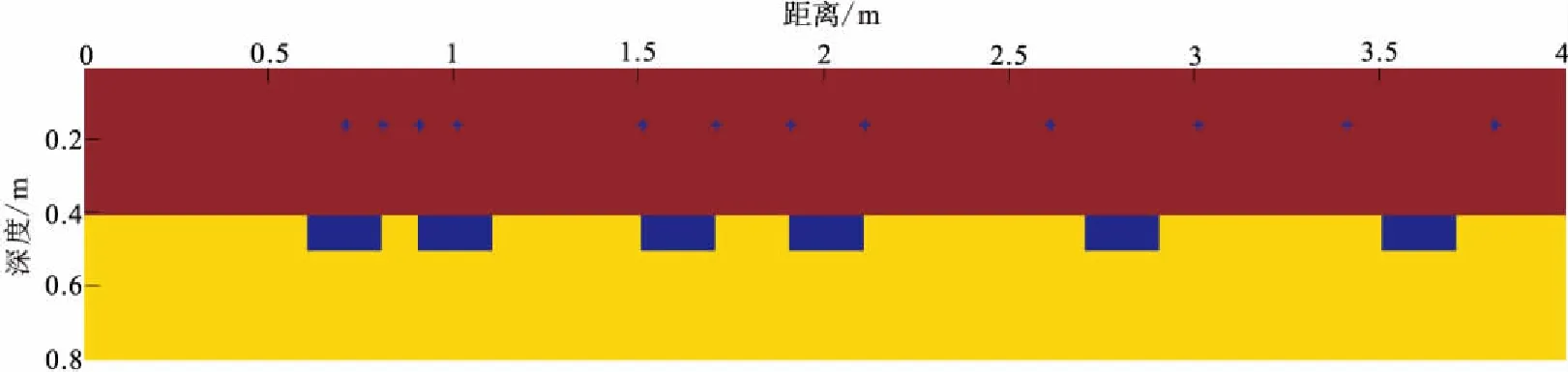
图1 不同密度的钢筋和钢拱架模型示意图Fig.1 Schematic diagram of different density and quantity of steel and steel grid frame model
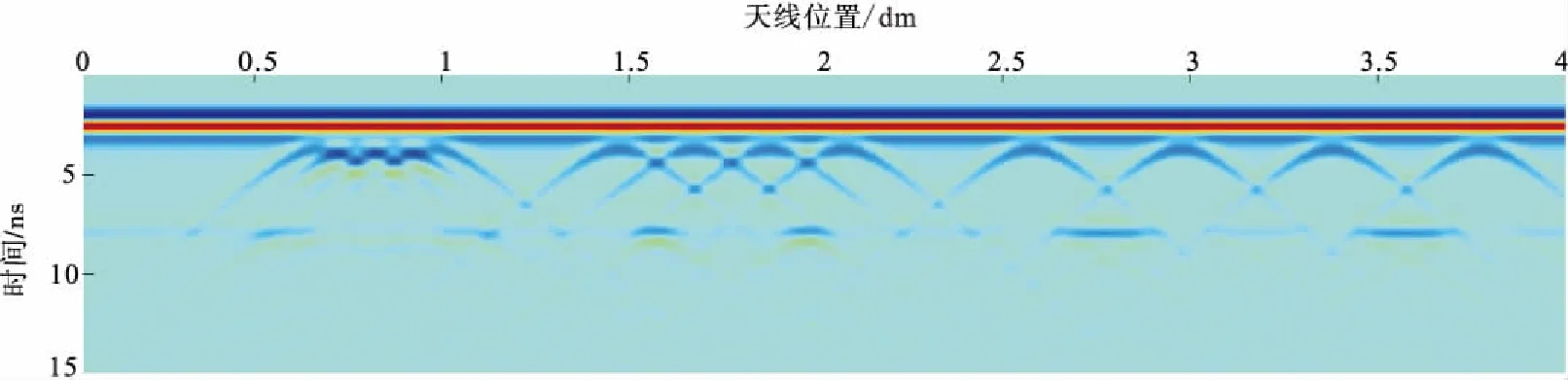
图2 500 MHz 天线钢筋和钢拱架正演模拟结果Fig.2 Steel and steel arch forward modeling results of 500 MHz antenna
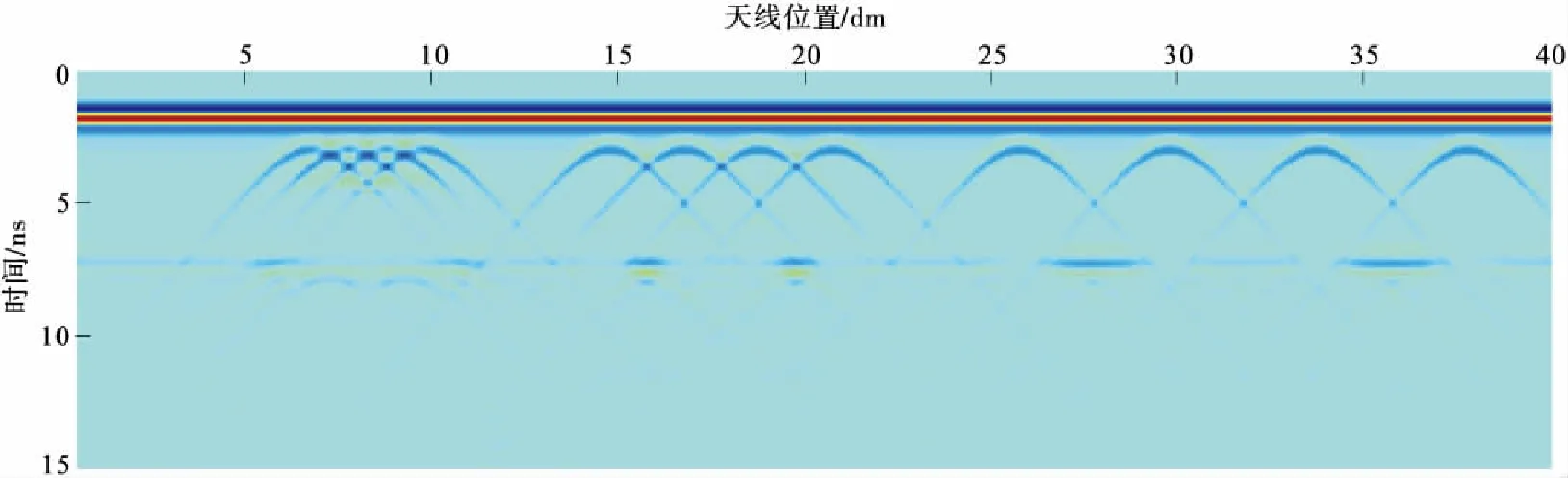
图3 800 MHz 天线钢筋和钢拱架正演模拟结果Fig.3 Steel and steel arch forward modeling results of 800 MHz antenna
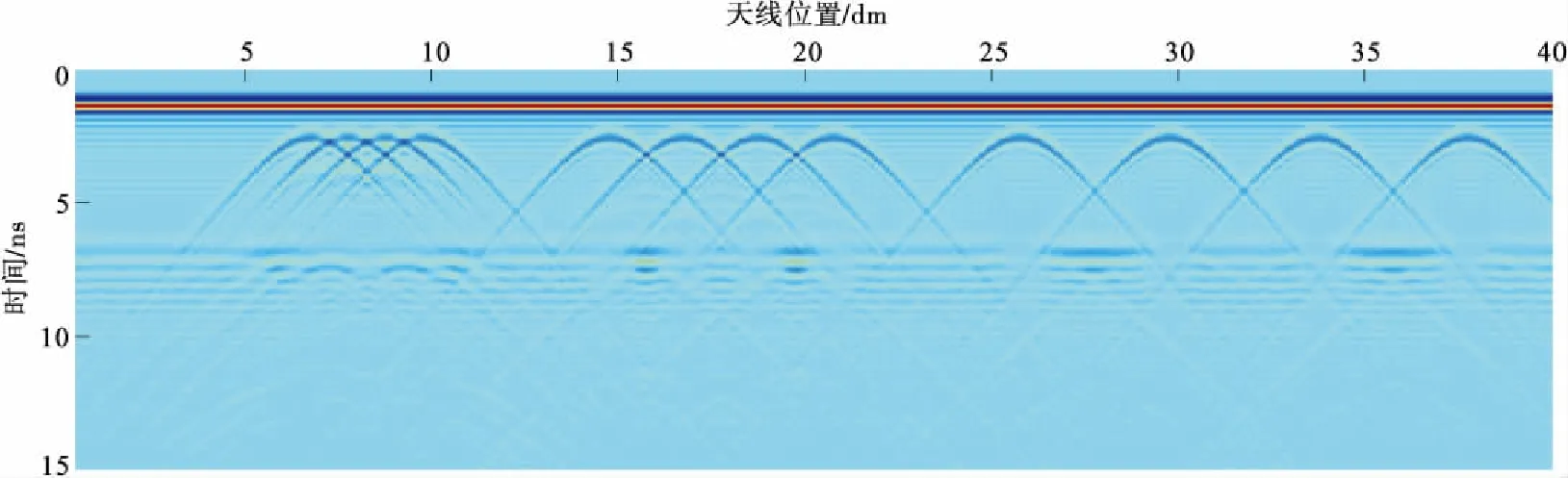
图4 1 200 MHz 天线钢筋和钢拱架正演模拟结果Fig.4 Steel and steel arch forward modeling results of 1 200 MHz antenna
由图2~图4可知,三种不同频率的天线正演结果均可以识别钢筋的数量和密度。弧形同相轴顶点(图中圆弧顶点)即为钢筋所在位置,弧形顶点间距即为任意2条钢筋的间距。但是由于反射电磁波受到钢筋散射干扰的影响,导致钢拱架的反射信号与多次反射波信号重叠,图像不清晰。如果钢筋网密度较大,例如间距为8 cm的4个钢筋,由于较为强烈的多次波干扰,使得分辨处于其下方的钢拱架十分困难。
由图2可知,中心频率为500 MHz的天线分辨率最低,弧形同相轴顶点较为模糊。其中,间距为8 cm的4个钢筋下方的钢拱架无明显波形,无法识别;间距为18 cm的4个钢筋下方的钢拱架波形与实际钢拱架长度不一致;间距为38 cm的4个钢筋下方的钢拱架波形与实际钢拱架的中心埋深和长度都较为一致。
由图3、图4可知,800 MHz和1 200 MHz中心频率的天线分辨率较高,能够准确识别不同密度的钢筋下方钢拱架的中心位置,并且在深度为0.4 m的位置,有一条从左至右能量较弱的水平同相轴,为混凝土和砂岩分界面。其中,对间距为38 cm的钢筋下方的钢拱架的埋深和长度能准确标出,为反射能量最强的水平同相轴所在位置。(图3、图4中出现能量相对较弱、交叉的多次反射波和绕射波,均是由于受到电磁波在有耗介质中的衰减和钢筋对电磁波的散射干扰的影响,其对围岩分界面反射信号的连续性也有影响)。
通过对图2~图4的分析可知,对于隧道衬砌的钢筋质量检测,可以选用高频的天线,在检测范围内都有较高的分辨率。但是,高频天线也存在缺陷,钢筋的散射干扰非常强烈,甚至淹没了钢拱架的实际位置和大小等信息。这种干扰可以通过K-F滤波等后期信号处理方法将干扰信号排除,以供解释人员准确识别目标体的反射信号[10- 11]。
2.4 衬砌脱空正演模拟
脱空是在衬砌施工期间隧道拱顶和拱腰位置常见的病害,是隧道二次衬砌浇筑混凝土振捣不当导致的收缩,围岩压力等方面因素造成的。
脱空是指隧道初衬与二衬之间较小范围的脱离区(可能充填空气或者水),或者是衬砌混凝土不密实或有小孔洞,可能会导致隧道衬砌出现裂缝,甚至导致开裂。
笔者模拟了隧道衬砌空间下的三种不同的脱空模型:①充气脱空模型;②充水脱空模型;③蜂窝状(密集小孔洞)模型(图5~图8)。钢筋的直径为2 cm,埋设深度为10 cm,钢筋间距为20 cm。每组脱空模型模拟实际问题中可能出现的三种不同的脱空形态:①圆形;②长方形;③三角形。圆形脱空的中心位置为(0.5,0.4),半径为10 cm;长方形脱空的中心位置为(1.5,0.4),长为40 cm、宽为30 cm;三角形脱空的中心位置为(2.5,0.4),是边长为30 cm的等腰直角三角形。蜂窝状模型把脱空充填介质改为不密实的蜂窝状,蜂窝状小孔洞内部充填介质为空气,以模拟衬砌混凝土不密实的情况。正演模拟参数:天线的中心频率为1 200 MHz。模型区域为3 m×0.8 m,天线采集道数为295。其它模型参数的设置与钢筋和钢拱架模型相同。混凝土、钢筋、砂岩、空气、水的电性参数参考表1。
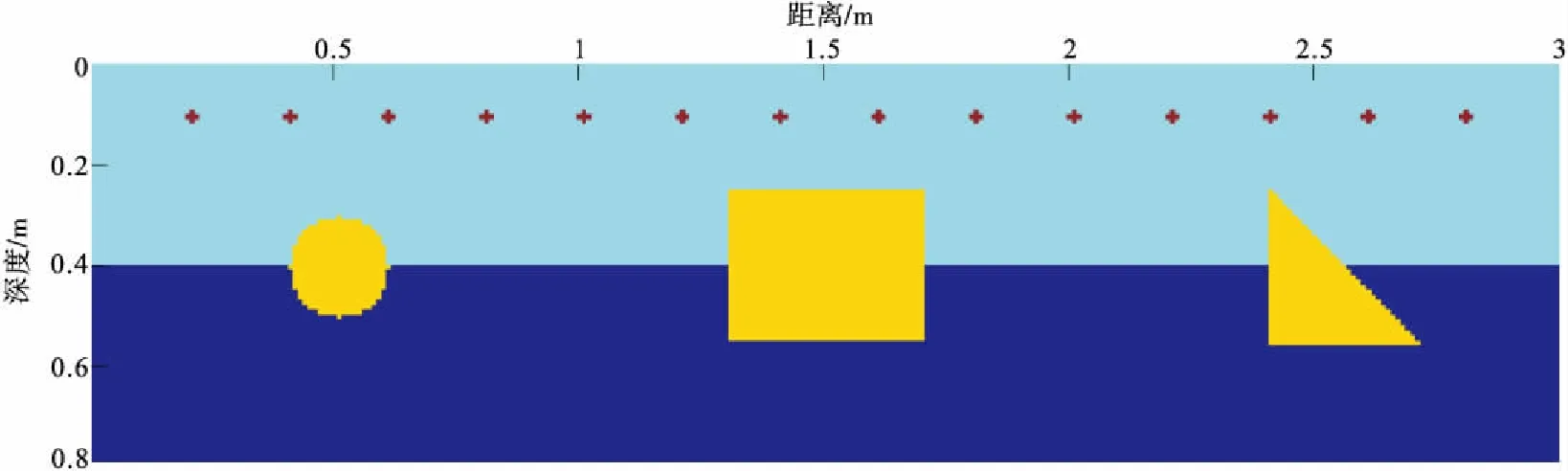
图5 不同形态的脱空区模型示意图Fig.5 Schematic diagram of different forms of cavity
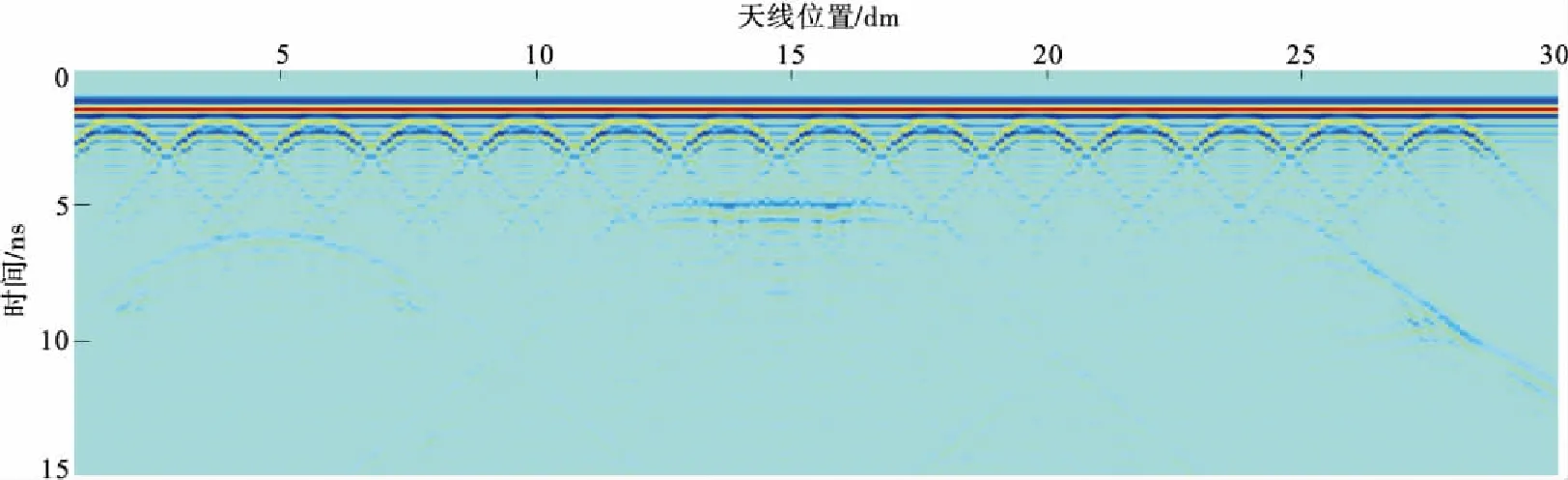
图6 1 200 MHz 天线充水脱空模型正演模拟结果Fig.6 Water filled cavity forward modeling results of 1 200 MHz antenna
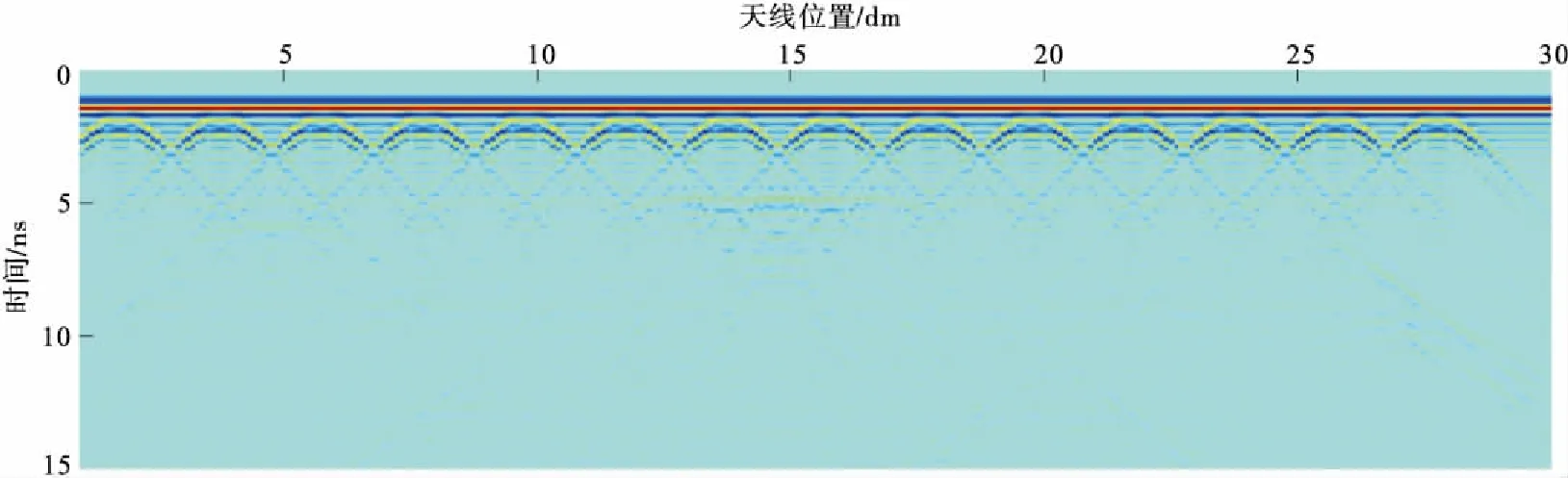
图7 1 200 MHz 天线充气脱空模型正演模拟结果Fig.7 Water filled cavity forward modeling results of 1 200 MHz antenna
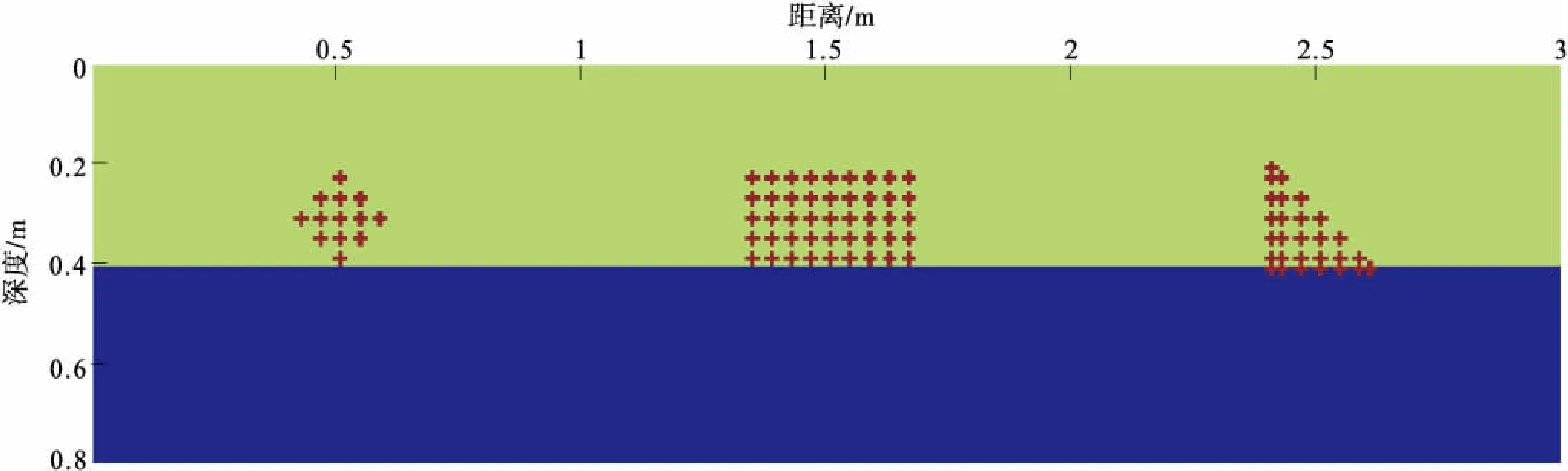
图8 蜂窝状模型示意图Fig.8 Schematic diagram of honeycomb cavity

图9 1 200 MHz 天线蜂窝状模型正演模拟结果Fig.9 Honeycomb cavity forward modeling results of 1 200 MHz antenna
由图6可知:对于圆形脱空模型,出现能量较强的弧形反射,且弧形反射同相轴的顶点位置为(0.5,0.15),其位置与模型设置的圆形脱空顶点位置一致,说明正演模拟能有效标出圆形脱空顶点的埋深和位置;对于长方形脱空模型,天线位置从左至右1.3 m~1.7 m,深度为0.15 m的位置,出现一条反射能量较强的水平同相轴,其位置与模型设置的长方形上部边界一致,说明正演模拟能有效标出长方形脱空上部边界的位置及其延伸长度;对于三角形脱空模型,天线位置从左至右2.45 m~3.5 m位置,出现一条与衬砌表面斜交的同相轴,与水平界面的角度大约为30°,模型设置的直角三角形上边界(斜边)位置为从左至右2.4 m~2.6 m,与水平界面的角度为45°。正演模拟结果与实际模型的位置和角度均有偏差,但是可以大致反映出三角形上边界的位置。分析原因,可能是由于充水脱空区域对电磁波能量的吸收而导致偏移。这种误差可以使用Kirchhoff积分偏移法等偏移方法将真实信号归位,准确反映目标体的位置信息[12]。
综上所述,利用中心频率为1 200 MHz的天线,对于隧道衬砌模型中,钢筋下面不同形状的脱空模型的大致埋深和位置均可以有效识别。但是受到脱空体上方钢筋的产生多次反射波的影响,对脱空体深度和位置的准确识别均有干扰,需要有经验的物探人员准确进行解释和识别。
图7为同样利用1 200 MHz的天线对充气脱空模型的正演模拟结果。区别于图6,图7中模型界面的反射能量相比于图6均较弱。因为由表1可知,空气、水、混凝土的电导率分别为0 s/m、30 s/m、0.005 s/m,空气与混凝土界面的反射系数相对较小。所以图7反射能量相对较弱,受到钢筋产生的多次反射波的干扰影响更大,不利于对脱空体的准确解释和识别。
由图8可知,蜂窝状模型也可以当作混凝土回填不密实的模型。小孔洞越密集,不密实程度越大,其模拟结果越接近脱空模型。
通过图9的正演模拟结果可知,衬砌与不密实区域界面的反射同相轴呈弧形,特别是小孔洞呈长方形分布的正演模拟结果,其密集小孔洞相叠加的多个反射波同相轴不连续,较为密集。
3 工程实例
3.1 检测方法
检测仪器采用pulseEKKO 型探地雷达,中心频率为1 200 MHz的天线,时窗为24 ns,采集方式为测轮距触发沿测线的连续测量。
探地雷达沿隧洞的拱顶、拱腰、边墙分别布置三条测线,测区布置如图10所示。
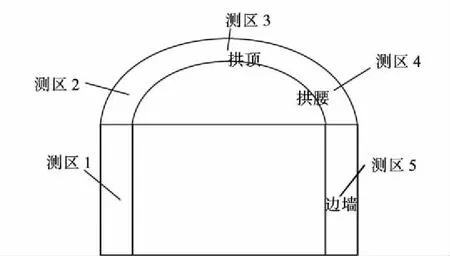
图10 测线布置示意图Fig.10 Sketch of measuring line
3.2 三种形状脱空和混凝土不密实病害实测结果
图11为云南玉溪市星云湖、抚仙湖出流改道工程隧洞衬砌混凝土质量检测图像。
1)由图11(a)可知,在测线位置6 227 m~6 233 m,时间轴6 ns~10 ns范围内,存在弧形反射信号,且反射能量强,推断该处为圆形脱空区产生的异常。经钻孔验证,该处确实存在圆形的充水小脱空区。对比图8发现,图8的充水圆形脱空区域,正演模拟结果显示时间轴在6 ns~10 ns范围内,有一条反射能量强的弧形反射信号。
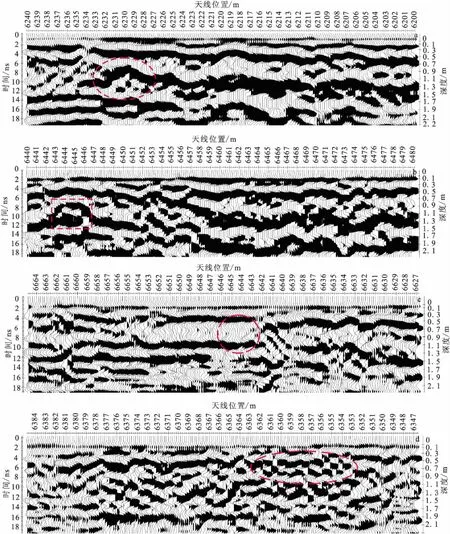
图11 探地雷达实测图Fig.11 Measured map of GPR(a)圆形脱空区;(b)长方形脱空区;(c)三角形脱空区;(d)混凝土不密实
2)由图11(b)可知,在测线位置6 442 m~6 447 m,时间轴6 ns~10 ns范围内,发育一条水平延伸的强反射能量的同相轴,且与两侧同相轴不在同一水平时间轴上,推断该处为长方形脱空区产生的异常。经钻孔验证,该处确实存在长方形的充水脱空区。对比图6发现,图6的充水长方形脱空区域,正演模拟结果为一条能量较强的水平反射信号,且其深度与两侧同相轴不一致。
3)由图11(c)可知,在测线位置6 639 m~6 642 m,时间轴4 ns~8 ns范围内,发育一条斜向延伸的强反射能量同相轴,且与右侧同相轴发生明显错段,推断该处为三角形脱空区产生的异常。经钻孔验证,该处确实存在三角形的充水脱空区。对比图6发现,图6的三角形脱空区,正演模拟结果为一条能量较强的斜向延伸的反射信号,且与右侧同相轴发生错段。
4)由图11(d)可知,在测线位置6 654 m~6 662 m,时间轴6 m~10 m范围内,同相轴不连续,波形断断续续,且较为密集,推断该处为混凝土不密实产生的异常。经钻孔验证,该处确实存在混凝土不密实的缺陷体。对比图9发现,图9的矩形不密实区,正演模拟结果为不连续的较密集的波形。
综上所述,由图11的4种不同异常的实测结果可知,主要异常信号与图6、图9的正演模拟结果反射信号都较为相似,且经钻孔验证,确实存在相似形状的混凝土病害。实测结果与钻孔揭露地质情况和正演结果都较为相符,达到了检测的目的。
因为本文正演模拟模型结构单一,只包含衬砌内部主要的结构和地质病害模型,因此我们采用的正演模拟方法的结果中,主要突出地质缺陷体的信号特征,不含噪音干扰。而实际的GPR探测结果与其相比,由于实际衬砌体内部构造的复杂性,有其他的噪音信号。但是实际探测结果的地质缺陷体异常信号与正演模拟基本一致,说明我们采用的正演方法可以指导实际工作。
4 结语
基于时域有限差分方法(FDTD)和完全匹配层(PML)的吸收边界条件,通过对隧道衬砌病害的探地雷达正演模拟及工程实例应用分析,可以得出以下结论:
1)探地雷达能较为快速高效、无损地识别衬砌质量如钢筋网和钢拱架的密度、衬砌脱空、混凝土不密实等问题,并且能够掌握充填不同介质、不同形状的脱空体的剖面图像特征。
2)利用GprMax软件结合Matlab编程,可以实现基于隧道衬砌模型的正演模拟,正演结果和实测剖面图的主要异常波形部分较为一致。
3)说明基于FDTD的雷达正演模拟,有助于更好地指导物探工作者对复杂的衬砌混凝土质量问题进行更精确地解释,同时也说明完全匹配层的吸收边界条件在混凝土质量检测雷达正演中的适用性。
4)对于正演结果中出现的绕射干扰和在频散介质中的偏移误差,可以结合K-F滤波和Kirchhoff积分偏移法等雷达信号处理方法,来对正演结果加以改进,进一步提高正演效果和解释精度。
[1] 徐赞.探地雷达在隧道初衬质量检测中的应用研究[J].地温建筑技术,2015,41(8):108-110. XU Z. Application of ground penetrating radar in quality detection of tunnel lining[J]. Geothermal construction technology,2015,41(8):108-110.(In Chinese)
[2] 王法刚,肖国强,尹健民.探地雷达在隧道衬砌混凝土质量检测中的应用[J].岩土力学,2003,24(增):183-185. WANG F G,XIAO G Q,YIN J M. Application of ground penetrating radar in quality detection of tunnel lining concrete[J]. Rock and soil mechanics,2003,24(S):183-185. (In Chinese)
[3] 钟世航,王荣.探地雷达检测隧道衬砌中的几个问题[J].物探与化探,2002(5):77-80. ZHONG S H,WANG R. Several problems in detection of tunnel lining by ground penetrating radar[J]. Geophysical and Geochemical Exploration,2002(5):77-80.(In Chinese)
[4] 李大心.探地雷达方法与应用[M].北京:地质出版社,1994. LI D X. Ground penetrating radar and its application[M].Beijing: Geological Publishing House,1994. (In Chinese)
[5] YEE K S.Numerical Solution of Initial Boundary Value Problem Involving Maxwell's Equations in Isotropic Media[J]. IEEE Transactions on Antennas and propagation,1966,14(3):302-307.
[6] BERENGER J P.Perfectly matched layer for the absorption of eletromagnetic waves[J]. Journal of Computation Physics,1994,114(2):185-200.
[7] 刘四新,曾昭发,徐波.探地雷达数值模拟中有损耗介质吸收边界条件的实现[J].吉林大学学报,2005,35(3):378-381. LIU S X,ZENG S F,XU B. Realization of lossy medium absorbing boundary conditions in the numerical simulation of Ground penetrating radar[J]. Journal of Jilin University, 2005,35(3):378-381. (In Chinese)
[8] 肖明顺,昌彦君,曹中林,等. 探地雷达数值模拟的吸收边界条件研究[J].工程地球物理学报,2008,5(3):315-320. XIAO M S,CHANG Y J,CAO Z L,et al. Study on the absorbing boundary conditions for the numerical simulation of ground penetrating radar[J]. Journal of Engineering Geophysics,2008,5(3):315-320. (In Chinese)
[9] 乔尔(Jol,H.M.).探地雷达理论与应用[M].雷太文,等译.北京:电子工业出版社,2011. JOEL (Jol, H.M.) Theory and application of ground penetrating radar[M].translation by LEI Tai-wen et al. Beijing: Electronic Industry Publishing House,2011. (In Chinese)
[10]TILLARD S,DUBOIS J C.Analysis of GPR data:wave propagation velocity determination[J]. Applied Geophysics,1995,33:77-91.
[11]JAYA M S,BOTELHO M A,HUBRAL P.Remigration of ground penetration radar data[J].Applied Geophysics,1999,41:19-30.
[12]邓世坤. 克希霍夫积分偏移法在探地雷达图像处理中的应用[J].地球科学—中国地质大学学报,1993,18(3):303-308. DENG S K. Application of Kirchhoff integral migration method in ground penetrating radar image processing[J]. Journal of Earth Science, China University of Geosciences, 1993,18(3):303-308. (In Chinese)
Simulation of tunnel lining concrete quality radar detection based on FDTD and its application analysis
ZHANG Yanga, XIAO Guoqianga, ZHOU Liminga, YU Xinjiangb
(Yangtze River Scientific Research Institute,a.Key Laboratory of Geotechnical Mechanics and Engineering of the Ministry of Water Resources,b.Engineering Safety and Disaster Prevention,Wuhan 430010,China)
For the tunnel lining may appear different geological diseases. According to the dielectric characteristic, we build the corresponding geophysical model based on the finite difference time domain (FDTD) algorithm and the perfectly matched layer (PML) absorbing boundary conditions, using GprMax software combined with Matlab programming to realize the forward modeling of GPR. The results show that the different density of reinforced with steel arch model, in different center frequency antenna forward results, affected by GPR resolution, reflected signal of different intensity and appearance. The phase, amplitude and waveform characteristics in different shapes of void model are not identical. Combined with the engineering application examples, GPR forward simulation results are basically matched with main abnormal waveform signal of measured profile results and drilling revealed condition. This shows that GPR can effectively detect the type, location, tectonic trends and spatial distribution characteristics of lining disease, and to verify the feasibility of the forward method. It is helpful to guide the geophysical workers to explain the quality of the lining more precisely, more accurately find the geological diseases of the lining, and to ensure the safety of the tunnel operation.
tunnel lining quality detection; ground penetrating radar (GPR); quality defects of different shapes; finite difference time domain algorithm(FDTD)
2016-07-15 改回日期:2016-08-06
长江科学院院所基金(CKSF2016045/YT)
张杨(1991-),男,硕士,主要从事工程物探和岩石力学理论与应用研究,E-mail:297380421@qq.com。
1001-1749(2017)04-0430-09
P 631.4
A
10.3969/j.issn.1001-1749.2017.04.02

