地震波与地层共振匹配的探讨与应用
黄德智, 孙 渊, 杨飞龙, 田 燚, 胡鹏飞, 陈继川
(1.长安大学,地质工程与测绘学院,西安 710054;2.西安石油大学,地球科学与工程学院,西安 710065;3.中国能源建设集团陕西省电力设计院有限公司,西安 710054;4.陕西省地质调查院,西安 710054)
地震波与地层共振匹配的探讨与应用
黄德智1, 孙 渊1, 杨飞龙2, 田 燚1, 胡鹏飞3, 陈继川4
(1.长安大学,地质工程与测绘学院,西安 710054;2.西安石油大学,地球科学与工程学院,西安 710065;3.中国能源建设集团陕西省电力设计院有限公司,西安 710054;4.陕西省地质调查院,西安 710054)
在地震资料采集、处理中,低信噪比资料和深部地震信号的信噪比提升非常困难,提高信噪比是该类地震资料处理中最关键的一环,是决定最终成像品质的关键。针对该问题,首先从地震波在粘弹性介质中的传播规律出发,详细分析了粘弹性介质对其内部传播地震波的频率、能量和信噪比的影响,总结了地震波在经过地下粘弹介质传播后频率、能量和信噪比的衰减规律和低信噪比地震资料的频率、能量特点;然后讨论了地震波与地下岩层的谐振,并分析了它们之间的谐振与地震资料频带、能量之间的关系,提出了通过改造地震记录频率使之与地下岩层共振频率带匹配来改善地震资料成像品质的观点;最后讨论宽带Ricker子波的原理及其优点,提出应用宽带Ricker子波对地震记录进行子波整形,最终实现地震资料与地层响应频率的匹配,从而提高地震资料信噪比的具体应用方法。该方法已在多个区域的地震资料处理中应用中,并取得了良好的应用效果。这表明,通过地震资料与地层响应频率匹配的方法,可有效地提高低信噪比地震资料的信噪比,为低信噪比地震资料的处理提供了一条具有参考意义的思路。
共振频率; 共振频率带; 宽带Ricker子波; 信噪比
0 引言
谐振是地下岩层固有的物理特征,它具有特定的响应频率。同时,不同岩性的地层也具有不同的响应频率,当人工激发地震波的频率与地下岩层的共振频率一致时,岩层会与人工地震波产生共(谐)振,这时人工地震波在岩层中产生的反射能量最强。对于地震资料采集来说,它有利于提高地震采集资料的信噪比(品质);对于地震资料处理来说,针对地层响应频率的特征进行资料处理,可提高地震剖面成像的信噪比,改善剖面的成像质量。从以上两个角度出发,地震资料频率与地层响应频率的匹配,是决定地震资料信噪比(成像品质)的关键因素。在实际应用中,宽带Ricker子波在实现地震资料(尤其是低信噪比地震资料)与地层响应频率的匹配、恢复优势谐振能量、提高地震成像剖面信噪比上具有较好的应用效果。
1 基本原理
1.1 粘弹性介质传播过程中能量吸收和频率衰减
地震波在粘弹性介质中传播时,部分能量转化为热能造成地震波能量损失。地层对地震波的吸收与地震波的频率成正比,与地层速度和品质因子成反比[1]式(1)、式(2)。品质因子Q值为一无量纲量,是在一个周期内(或一个波长距离内)振动所损耗的能量与总能量之比的倒数。
A=A0e-αr
(1)
其中:A为振幅;A0为初始振幅;α为吸收系数;r为半径。
α=πf/Qv
(2)
其中:α为吸收系数;f为频率;Q为品质因子;v为纵波速度。
通过式(2)我们可以看出,地层的吸收系数与地层的Q值跟地震波在地层中传播的速度成反比,与地震波的频率成正比。Q值越大、速度越大、频率越低,地层吸收系数越小,地震波的能量衰减就越小;反之Q值越小、速度越小、频率越高,地层吸收系数越大,地震波的能量衰减就越大,地层的吸收作用就越显著。从这一角度来说,对于较低频率成分的地震波,粘弹性介质对其的吸收相对较小;对于较高频率成分的地震波,粘弹性介质对其的吸收相对较大。
综合式(1)和式(2)可知,人工激发地震波在粘弹性介质中传播的过程中,由于地层的吸收作用及波前面的几何扩散,高频信号能量随传播距离变大而不断衰减,当某一频率的高频信号能量衰减到一定程度时,可认为该频率地震波被地层完全吸收。因此,地震波在粘弹性介质中传播过程中,也是高频信号不断被地层吸收的过程,地震波的频率和能量逐渐降低。另一方面,地震波前面的能量与其振幅的平方、频率的平方及介质密度成正比[2]:
(3)
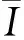
综合以上,地震波能流密度是单位面积上地震波波前面的能量,在一定程度上意味着地震资料的信噪比。某一层粘弹性介质中地震波的传播速度和介质密度是固定的,在地震信号频率较低、振幅较低的情况下,地震信号的能量就弱,这是产生低信噪比地震资料主频较低的原因。低信噪比地震资料的有效频带相比于信噪比较高资料的有效频带应该变窄而且向低频端移动。基于同样的原因,深部地震勘探由于地震波传播距离过长,它的有效频带也会向低频端移动。
1.2 固有响应频率与激发地震波的共振
共振是某一物理系统在特定频率下,比其他频率以更大的振幅做振动的情形,产生共振的特定频率称为共振频率。无论力学、声学、电子等物理系统,一个物理系统有多个共振频率,并且在这些频率上会产生共振,在其他频率上不会产生共振。如果是一个频率比较复杂的振动(如宽频振动),系统会将其他频率过滤掉,而与其共振频率相同的振动产生共振。在共振频率下,很小的周期振动便能够在产生共振的物理系统中产生很大的振动,因为该物理系统储存了动能。当系统的阻尼很小时,共振频率基本与系统的自然频率(固有频率)相等;当系统的阻尼高时,则会产生较宽的共振频率带。在共振频率带中,固有频率的振幅是最大的。
地震波在地层中传播的过程中,地层也会同地震波中与地层共振频率相同的振动产生共振。因为地下地层为粘弹性介质,阻尼系数一般相对较高,所以地层产生的共振为一个共振频率带。从信号角度来说,地层的共振响应频带是地层对于地震勘探人工激发地震波的一个滤波器,在地层对地震波的滤波过程中,如果激发地震波的频带与地层的共振频率相同,地层会对地震波产生共振响应,这时接收的地震波能量最强。从这个角度来看,如果在地震资料处理过程中地震资料以地层共振响应频率为基础进行处理,地震资料的信噪比会得到提升。
因此,从共振的角度出发,地震资料采集时应该使激发地震波的频带尽量与地层的固有响应频率接近,这样接收到地震信号的信噪比才会更高。在地震资料处理时,如果地震资料的频带和地层共振响应频率带一致的话,地震剖面成像的信噪比会得到提升,尤其是低信噪比资料。
1.3 固有频率与地震反射波共振频率的确定
虽然不同地层间的共振频率各不相同,但是它们之间的共振频率带有相互重叠的部分。地震波在两套地层之间传播时,传出地层所传出的地震波是经过传出地层共振响应滤波改造后的地震波,其频率是以传出地层的共振频率带为基础。同时,地震波在接收地层传播时,接收地层会与传入的地震波中跟自己共振频率一致的地震波产生共振,从而对地震波进行滤波改造,使之与自己共振频率带一致。由此可见,地震波在地下岩层中的传播过程中,每经过一套地层后其频率特性就要被改造一次。因此,我们每个时刻接收的地震波是在传播过程中所经过的所有地层共同改造的结果。由于地震波本身的特质,由浅至深频率逐渐降低,对于地层而言,深部地层只有谐振频率在地震波的频率范围内才会与其谐振。因此,地震记录由浅至深,频率逐渐降低。
当把地震波由激发点到接收点所有经过的岩层看成是一个整体系统时,那么这个系统的共振频率带应该是各地层的固有共振频率带共同滤波作用而产生的一个共振频率带(图1)。这个滤波系统的共振频率,是地震波传播所经过各地层的共同作用的结果,在地震记录中表现为频谱中能量最强的频率,有些情况下它也可以表现为一个频率不宽的共振频带。
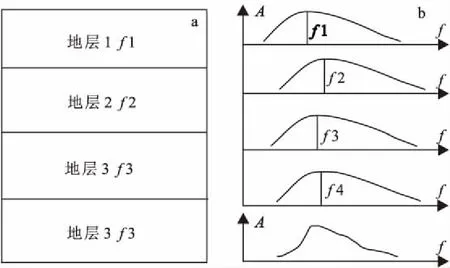
图1 地震波与地层共振响应频谱示意图Fig.1 The relationship between seismic wave and layer resonance(a)四套地层和各自对应的共振频率;(b)各地层的共振频率带示意图
但在两种情况下,我们可以将所有地层近似看成一个整体响应系统:
1)如果激发所产生的地震波能量较弱,在地震记录时间上由小到大,深度上由浅至深地震波的频率成分比较接近的情况,我们可以模型简单化,将其看成一个整体的响应系统。
2)如果由浅至深,虽然存在不同地层,但各层间的基频频率基本接近且地层的吸收作用弱,那么在一定深度范围内,地震信号向低频端降低的幅度会非常小,我们也可以将其视为一个整体的地层响应系统。
对于满足上述理论要求的勘探区域而言,我们可以按同一共振频率来进行地震资料处理(图2)。

图2 地震数据频谱分析图Fig.2 The frequency spectrum of seismic data
1.4 共振频率及其倍频对地震波能量的影响
由式(4)可知,如果地震波的频率为2f,我们也可以把它的频率看作f。基于此,频率为3f、4f等以f为基频的地震波也可以看成频率为f的地震波,如果将此类地震波与频率为f的地震波叠加可增加f频率地震波的能量(式5)。
A=A0cos(2πft+t0)
(4)
其中:A为振幅;A0为初始振幅;f为频率;t0为初始时间。
A=A0cos(2πft+t0)+A1cos(4πft+t0)+
A2cos(6πft+t0)+A3cos(8πft+t0)
(5)
其中:A为振幅;f为频率;t0为初始时间;A0为f频率初始振幅;A1为2f频率初始振幅;A2为3f频率初始振幅;A3为4f频率初始振幅。
图3为一个周期的f(系列1)、2f(系列2)、3f(系列3)、4f(系列4)四种频率余弦波与它们直接叠加结果(系列5),这里的叠加结果相当于我们接收到的地震波信号。通过该图,我们可以看到叠加后的余弦波的波形和能量与基频余弦波的波形和能量差异非常明显。在基频地震波与倍频频率地震波的叠加过程中,叠加时在基频的波谷处会与倍频的波峰叠加,振幅会产生相互抵消作用,使得地震信号波谷处能量变弱。从示意图中可以看到,如果波谷处倍频成分能量叠加后超过基频,甚至会发生波谷变波峰。这样会出现假频现象,从而造成视频率提高。
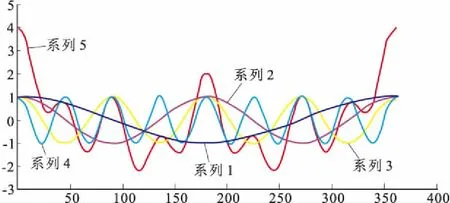
图3 基于倍频的余弦波叠加效果图Fig.3 The superposition of frequency-doubling cosine wave
综上所述,我们接收地震信号有效频带的最高频率一般为最低频率的几倍。由此可知,地震波中地层共振频率的倍频信号对地震波中的共振频率信号有一定的抵消作用。因此,我们在地震资料处理过程中(尤其是低信噪比地震资料处理过程中)应尽量消除相关地影响,以突出共振频率信号来提高地震剖面的信噪比。具体来说,就是在地震数据处理过程中,应关注相对频率较低的共振频率信号的能量、相位的波形恢复工作。
1.5 宽带Ricker子波
宽带Ricker子波[3]-[15](图4)是由不同宽度Ricker子波合成的子波具有主瓣比较窄、旁瓣幅度小、波形简单的特点[3]。在主瓣宽度相同的情况下, 其振幅谱的峰值频率比较低,使得其在保真度和信噪比方面优于常用的带通子波和Ricker子波。其表达式为
(6)
其中:g为频率参数;p和q是Ricker子波式中参数g的积分限。
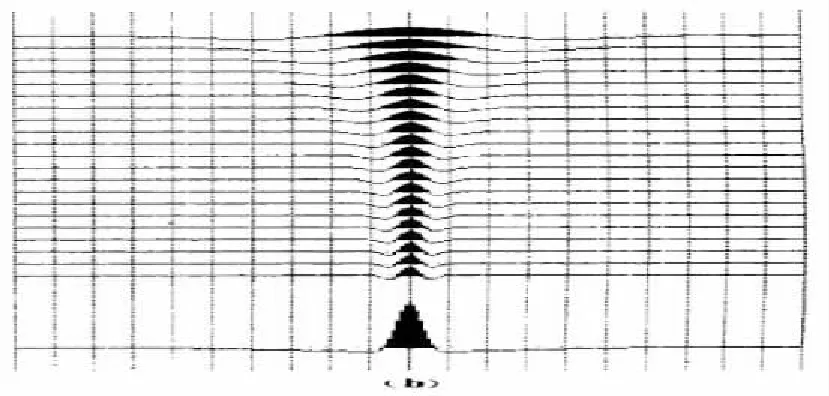
图4 宽带Ricker子波的合成Fig.4 The synthesis of wide-band Ricker wavelet
宽带Ricker子波振幅谱的峰值频率远低于主瓣等效频率[3](图5),其向低频方向下降的陡度大,有利于衰减噪声的低频成分,特别是面波;其向高频方向下降的陡度小,有利于对高频噪声的压制。
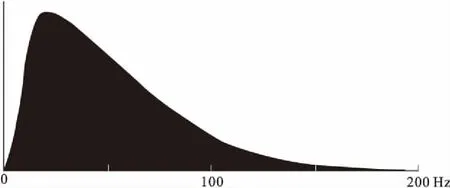
图5 宽带Ricker子波的振幅谱Fig.5 The spectrum of wide-band Ricker wavelet
利用宽带Ricker子波的滤波特性对地震记录进行改造, 若宽带Ricker子波的峰值频率与地层的谐振频率一致(即最高信噪比的频率),可以得到地层共振响应频率一致的地震记录,从而实现提高地震记录和地震剖面的信噪比。因此,在处理过程中可以通过宽带Ricker子波对记录进行反褶积整形, 部分达到地震记录与地层响应频率匹配的目的。
2 应用及效果分析
实际应用中,首先在炮集记录上提取统计子波(最小相位), 根据不同的期望子波做反褶积处理;然后在共接收点道集上提取统计子波(最小相位或零相位), 根据不同的期望子波进行反褶积处理。该方法不仅能校正压缩激发震源子波波形,还可以消除地表响应。从这个意义上讲,它具有一定的地表一致性反褶积效果,从而达到恢复共振响应频率地震波的波形。
图6至图11是两个通过调整地震资料主频,使之与地层的谐振频率一致,从而提高地震资料信噪比的实例。从图6可以看到,记录频率调整到谐振频率后,声波、面波和线性干扰得到明显压制,反射波信噪比得到明显提高;从图7可以看出,调整后速度谱的杂乱能量团得到明显压制,有效反射能量的速度趋势变得明显,速度谱质量得到提高;从图8可以看到,调整到谐振频率后的叠加剖面信噪比提高明显。
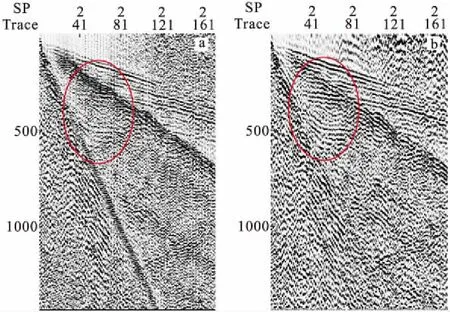
图6 实例一共振频率调整前后地震记录对比Fig.6 The comparison of frequency adjusted seismic data and original seismic data of the first example(a)调整前;(b)调整后
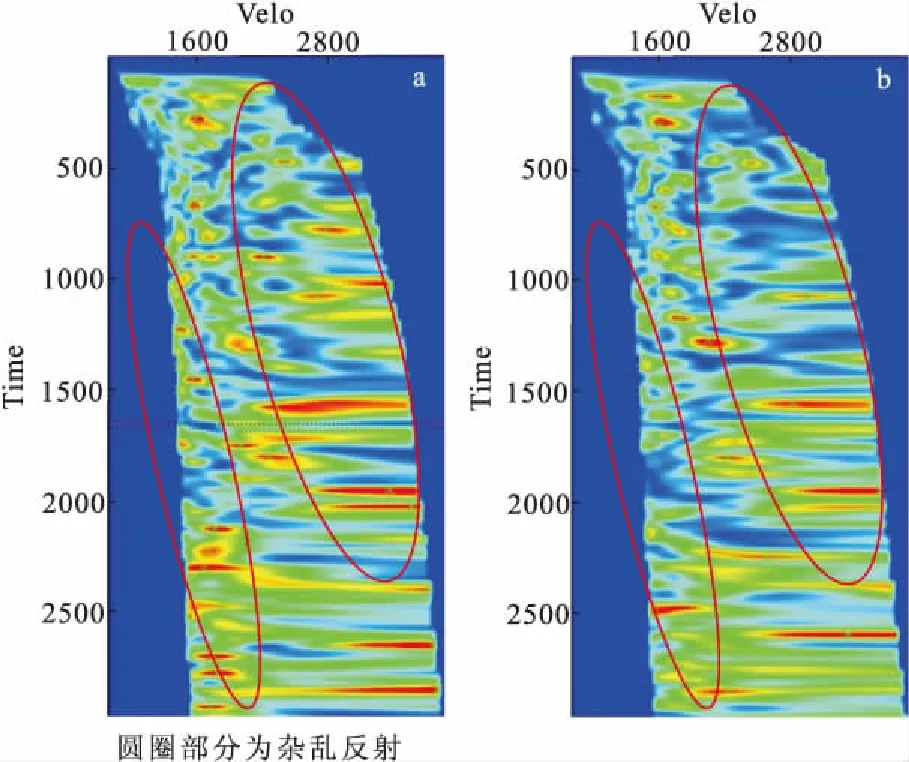
图7 实例一共振频率调整前后速度谱对比Fig.7 The comparison of frequency adjusted velocity spectrum and original velocity spectrum of the first example(a)调整前;(b)调整后
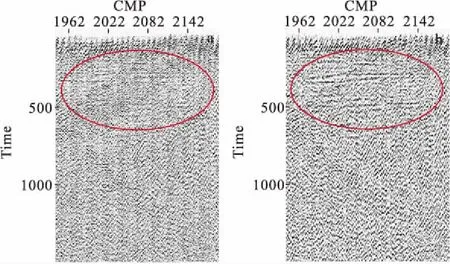
图8 实例一共振频率调整前后地震叠剖面对比Fig.8 The comparison of frequency adjusted section and original section of the first example(a)调整前;(b)调整后

图9 实例二共振频率调整前后地震记录对比Fig.9 The comparison of frequency adjusted seismic data and original seismic data of the second example(a)调整前;(b)调整后
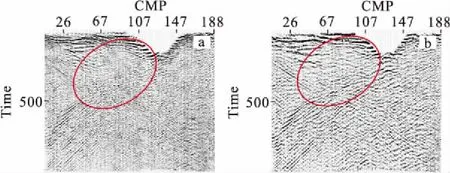
图10 实例二共振频率调整前后地震叠剖面对比Fig.10 The comparison of frequency adjusted section and original section of the second example(a)调整前;(b)调整后
从图9可以看出,在频率调整前记录上500 ms~1 000 ms有较弱的绕射波和断面波,反射波不明显;调整之后绕射波和断面波信噪比的到明显提高,同时浅层出现反射波。从图10可以看出,经过频率调整后地震剖面的成像变得清晰,信噪比提高明显。从图11可以看到,叠前去噪后叠加剖面信噪比得到进一步提升,偏移剖面反映的地质现象非常清楚,能够清楚地揭示该测线下的真实地质情况。
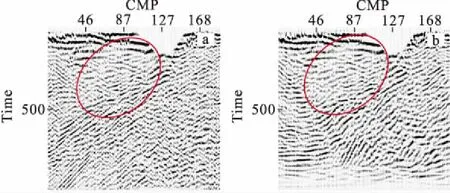
图11 实例二经共振频率调整后的叠前去噪 剖面及偏移剖面Fig.11 The prestack noise elimination section and migration section of the second example(a)叠前去噪剖面;(b)偏移剖面
通过两个实例可以看出,经过频率匹配处理后,地震剖面的信噪比提高明显,由倍频等引起的视假频也有所压制。
3 结论
1)一个地震勘探区域是一个滤波物理系统,它会将频率与自己共振频率带一致的地震波放大,其他频率的地震波会被压制。因此,基于地震波与地层共振的原理,地震资料采集时应使激发地震波的频带尽量与地层的共振频率带一致,这样激发的地震波能量才会最强,接收到地震信号的信噪比才会更高;在地震资料处理过程中,尤其是低信噪比地震资料,确定地下地层的谐振频率,使地震资料频率与之相匹配,做好共振频率地震波的能量、波形和相位恢复工作,可有效提升地震成像剖面的信噪比。
2)现在的地震数据的采集、处理以及相关地震软件的研发,主要偏向于提高地震剖面的分辨率(频率)方面,基本没有考虑到地层系统的共振对地震资料的影响。在高信噪比地震资料采集、处理过程中,这方面的影响不是十分突出,但在低信噪比地震资料和深部地震勘探中,这方面的影响就变得非常突出。因此,在这类地震勘探中,针对地层共振响应方面研究的意义就变得非常重要。
致谢
感谢西安石油大学李辉峰教授为本文的完成提供了大量有益的建议。
[1] 李振春,张军华.地震数据处理方法[M].东营:中国石油大学出版社,2004. L Z C, ZHANG J H. The method of seismic data processing[M].Dongying: China University of Petroleum press, 2004.(In Chinese)
[2] 杜世通.地震波动力学[M].东营:石油大学出版社,1999. DU S T. Dynamics of seismic wave [M]. Dongying:China University of Petroleum press,1999. (In Chinese)
[3] 俞寿朋.宽带Ricker子波[J].石油地球物理勘探, 1996,315(5):605-615. YU S P. Wide-band Ricker wavelet [J]. Oil Geophysical Prospecting, 1996, 31(5):605-615. (In Chinese)
[4] 梅金顺,王润秋.Ricker类地震子波[J].石油地球物理勘探,2012,47(s):8-14. MEI J S, WANG R Q.Ricker Seismic wavelet[J].Oil Geophysical Prospecting,2012,47(s):8-14. (In Chinese)
[5] 蔡希玲.俞氏子波在地震数据处理中的应用研究[J].石油地球物理勘探,2000, 35(4):497-507. CAI X L. Application of Yu wavelet to seismic data process[J].Oil Geophysical Prospecting,2000,35(4):497-507. (In Chinese)
[6] 邓巧琳.地震波在反射与透射影响下的能量衰减分析[D].长沙:湖南大学,2013. DENG Q L.Derivation of reflection and transmission coefficients of seismic waves in viscoelastic media[D].Changsha:Hunan University,2013. (In Chinese)
[7] 魏文,李红梅,穆玉庆.中心频率法估算地层吸收参数[J].石油地球物理勘探,2012,47(5):735-739. WEI W, LI H M, MU Y Q,et al. Estimation of stratigraphic absorption parameter based on center frequency method[J].Oil Geophysical Prospecting,2012,47(5):735-739. (In Chinese)
[8] 韩海英,王志章,王宗俊,等.基于Ricker类地震子波的匹配追踪[J].石油物探,2014,53(1):17-25. HAN H Y, WANG Z Z, WANG Z J,et al.Matching pursuit based on Ricker-like seismic wavelet[J].Geophysical Prospecting for Petroleum,2014,53(1):17-25. (In Chinese)
[9] 云美厚,丁伟.地震子波频率浅析[J].石油物探,2005,44(6):578-581. YUN M H, DING W. Analysis of seismic wavelet frequency[J].Geophysical Prospecting for Petroleum,2005,44(6):578-581. (In Chinese)
[10]何宝庆,王秋成,蔡锡伟.地震波场数值模拟中的信号恢复问题[J].石油物探,2008,47(4);357-360. HE B Q, WANG Q C, CAI X W. Signal restoration in numeral simulation of seismic wave field[J].Geophysical Prospecting for Petroleum,2008,47(4);357-360. (In Chinese)
[11]胡世丽,王星,王观石.子波穿过黏弹性节理的波形变化规律[J].有色金属科学与工程,2014,5(6):89-94. HU S L, WANG X, WANG G S.Waveform change rule of wavelet across viscoelasticity joint[J].Nonferrous Metals Science and Engineering,2014,5(6):89-94. (In Chinese)
[12]高倩,李仲东,赵爽.基于子波分解的含气性识别技术在CC地区浅层气藏勘探中的应用[J].天然气地球科学,2011,22(3):549-553. GAO Q, LI Z D, ZHAO S. Application of gas-recognition technology based on wavelet[J].Natural Gas Geoscience,2011,22(3):549-553. (In Chinese)
[13]刘浩杰,王延光.地震资料分辨率若干问题的探讨[J].油气地球物理,2009,7(4):5-11. LIU H J, WANG Y G. Discussion of some questions on resolution for seismic data[J].Petroleum Geophysics, 2009,7(4):5-11. (In Chinese)
[14]涂远艮,王达远,李华科.川西坳陷地震波衰减定量估算及分析[J].物探与化探,2013,37(4):596-602. TU Y G, WANG D Y, L H K. Quantitative calculation and analysis of sesmic wave attenuation[J]. Geophysical and Geochemical Exploration,2013,37(4):596-602. (In Chinese)
[15]马灵伟,顾汉明,李宗杰,等.应用正演模拟分析近地表黏弹性对深层缝洞储层地震波衰减及成像的影响[J].石油地球物理勘探,2014,49(4):694-701. MA L W, GU H M, LI Z J,et al. Near surface visco-elastic medium influences on wave attenuation and imaging of deep fractured-vuggy reservoir with forward modeling[J].Oil Geophysical Prospecting,2014, 49(4):694-701. (In Chinese)
Discussion and application between seismic wave and layer resonance matching
HUANG Dezhi1, SUN Yuan1, YANG Feilong2, TIAN Yi1, HU Pengfei3, CHEN Jichuan4
(1.Geology Engineering and Geomatics, Chang'an University, Xi'an 710054, China;2.School of Earth Sciences and Engineering, Xi'an Shiyou University, Xi'an 710065, China;3.China Energy Engineering Group Shaan Xi Electric Power Design Institute Co., Ltd. Xi'an 710054, China;4.Shaanxi Geological Survey Institute, Xi'an 710054, China)
It is very difficult to improve which the signal-noise ratio of the seismic data with either low signal-noise ratio (SNR) or the deep depth. To improve the SNR of eismic data is a key issue in seismic data process. For this problem, we first analyze the change of frequency, energy and signal-noise ratio of seismic wave which seismic wave spread in viscoelastic medium in this paper. The affect to the SNR of the seismic data from the relationship between seismic wave and layer resonance is analyzed. We then suggest that seismic data is reformed to matching layer's resonance frequency. The principle and advantages of wide-band Ricker wavelet is finally studied, suggesting that wide-band Ricker wavelet reform seismic data is used to matching layer's resonance frequency. The method has been applied to the seismic data processing in many regions, and good results have been achieved. This shows that the method of matching the seismic data and the formation response frequency can effectively improve the SNR of seismic data with low SNR, which provides a reference for the processing of low signal-noise ratio seismic data.
resonance frequency; band of resonance frequency; wide-band Ricker wavelet; signal-noise ratio
2016-02-04 改回日期:2017-03-30
黄德智(1976-),男,硕士,主要从事地震资料处理及研究工作, E-mail:410821265@qq.com。
1001-1749(2017)04-0558-07
P 631.4
A
10.3969/j.issn.1001-1749.2017.04.17

