雷达拼图射线状杂波抑制算法及其应用

福建省气象信息中心 袁 伟 高 攀 郑玉兰

雷达拼图射线状杂波抑制算法及其应用

福建省气象信息中心 袁 伟 高 攀 郑玉兰

从雷达产品拼图中出现的射线状杂波出发，研究其产生的机理与特征，并在大量统计分析的基础上，建立相应的射线状杂波筛选、去伪存真和逐点抑制的检验模型，同时对模型中用到的检验参数进行了分析与论证。该文设计的射线状杂波筛选游程算法，可以有效定位雷达产品数据中的射线状杂波，应用强相关性检验算法和T-值检验算法进一步得到更加可靠的射线状杂波数据，最后设计格点平移窗口对射线状杂波数据进行逐点抑制。三个步骤的抑制算法过程实施后，能够改善雷达拼图效果，在射线状杂波对天气过程判断造成的干扰有一定的抑制作用。

雷达拼图 射线状杂波 检验模型 游程算法 强相关性检验

多普勒天气雷达在短临、台风、暴雨等天气过程预报中起的作用已越来越重要。其观测产品数据、小时累计降水产品、基本反射率、组合反射率、回波顶高、基本速度等十几个直接产品和几十种衍生产品已应用到不同场合下天气预报预测中[1]。与此同时，在雷达观测数据的质量控制研究方面，国内外也做了大量的技术研究与应用[2-5]，并取得了非常有价值的成效，由于雷达产品因种类繁多、应用广泛，仍存在部分没有质控或质控算法未普及到的地方，给实际预报预警判断上会带来一定的困扰。

雷达基本反射率、组合反射率产品是雷达最基本的产品，常以一定区域范围内多部雷达进行拼图的形式展示出来，在降水动态监测预警中直观、形象，对预报员而言，有很强的既视感，如图1所示。

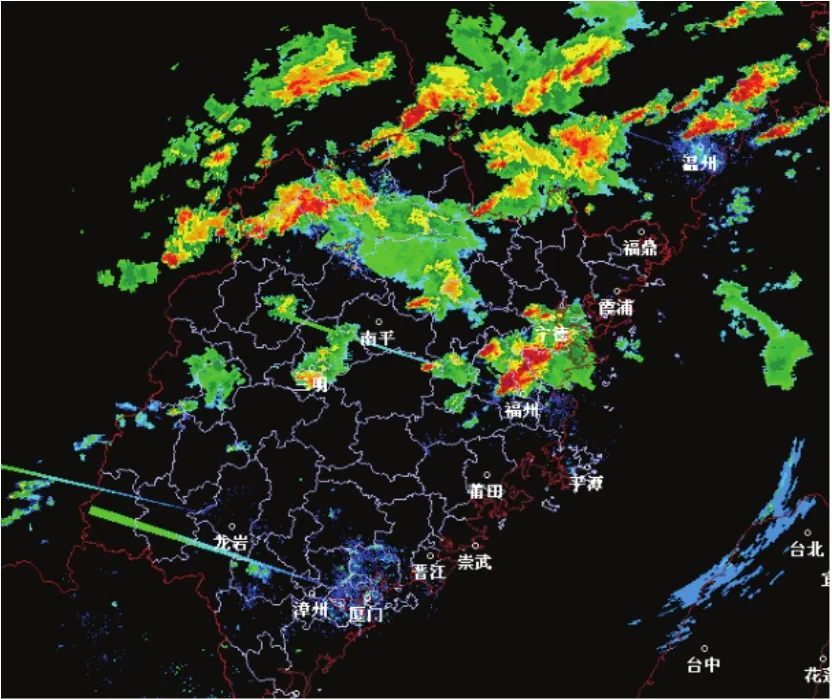
图1 基本反射率多部雷达拼图实况

雷达拼图产品在实际应用中，时有一些射线状的杂波出现，对预报员准确判读产生了一定干扰影响，同时也存在回波图像遮挡等问题。本文将对雷达拼图中出现的射线状杂波进行研究，并提出相应的抑制方案和实现过程，试图最大可能的还原真实回波图像。

1 雷达拼图中射线状杂波抑制概述

分析雷达拼图产品中出现射线状雷达回波的数据，可以发现它有几个特点：（1） 常常以一根或多根孤立的线段存在，而周边没有回波。（2）线段出现在扫描线的末端居多。（3）线段上的回波强度一般不强，且大部分在中间值左右。（4）同一扫描线上，除该线段外，没有更长的其他线段。

当多部雷达进行产品拼图时，单站的射线状杂波可能会遮盖周边雷达探测的有效数据，造成不必要的误判，而且这类射线本身没有实际上的天气现象含义，但其往往与真实的降水回波叠加在一起，容易造成人工识别上的困扰。因此抑制这类非天气过程引起的射线状杂波，有一定的研究价值和意义。

根据上述特点，本文将追溯到拼图产品来源的单站雷达产品，展开相应的技术分析，试图建立一个较为客观的射线刻画模型，遵循用模型算法定位射线，然后加以抑制，从而达成拼图产品中剔除射线的研究目标。

2 射线状杂波抑制算法

由于雷达拼图的数据来自雷达单站产品，通过研究单站雷达产品的特征，采用射线状杂波筛选、伪射线状杂波剔除、相邻射线状杂波抑制、基准射线状杂波抑制等措施，最终实现去伪存真、有效抑制射线状杂波的算法。

下面的研究将以单站雷达基本反射率19号产品为例进行分析论证,其回波强度量化后从0～15分为16个等级，值越大表示回波越强，这里我们称之为能量值。

2.1 射线状杂波筛选

单站雷达产品数据上射线状杂波的特征，主要体现在：孤立的一条射线，射线上回波较强，周边回波非常弱（量化后一般为零），射线长短不一，粗细不均等。根据这些特点，设计回波游程统计，相对集中的能量判决算法，初步过滤出射线状杂波。

针对单站雷达产品，每条扫描线上，统计游程：

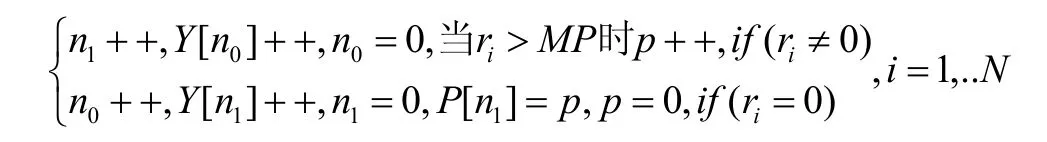
其中N为扫描距离数；ri为扫描线上第i个扫描距离的回波值；n0、n1分别为扫描线上回波值为0和非0时的连续统计计数；Y[n0]、Y[n1]分别为统计连续回波为0和非0出现的距离数长度计数。p为连续能量计数器，MP =8为能量中值，P为连续非0距离数的回波能量累加和。

记游程Y[n0]最大值所对应的距离长度为Md0。记游程Y[n1]最大值所对应的距离长度为Md1，此时相应的能量为P[Md1]。记游程Y[n1]第二大值所对应的距离长度为d1。

则满足如下条件的扫描线可定为疑似射线状杂波：

(1)Md1/N >0.5，有回波的最大距离长度超过总长度的一半以上。

(2)P[Md1] < 1，能量值控制在一般回波强度范围内，即要求不出现特别强的回波。

或

(1)（Md0+ Md1）/N > 0.8，有回波值和无回波值的距离长度之和占据大部分扫描线。

(2)P[Md1] < 1能量值控制在一般回波强度范围内，即要求不出现特别强的回波。

(3)d1/ Md1 < 0.5，有回波的第二长度的距离数不超过有回波的最大距离长度一半。

上述判决条件是基于2017年2月份中15000个文件（总计5788562条扫描线）的数据统计分析情况而定。设定几个中值进行比较，统计结果见表1～表3。

表1 有回波的最大距离长度与总长度占比分析

表2 有回波值和无回波值的距离长度之和与总长度占比分析

表3 有回波值的第二距离数与第一距离数比率分析

统计表中的偏好系数为：估算射线数（样本比率乘以疑似文件数）与疑似射线的比值，其值越大表明筛选效果越好。综合表1～3结果分析，在筛选射线状杂波时，为尽可能的选入存在射线状杂波的数据（偏好系数相差不大的情况下，选稍小比率或占比），可选取如下门限参数：①有回波的最大距离长度与总长度占比=0.5；②有回波值和无回波值的距离长度之和与总长度占比=0.8；③有回波值的第二距离数与第一距离数比率=0.5。

2.2 伪射线状杂波剔除

经过射线状杂波筛选预处理后，大部分射线状杂波文件能够选入，但仍然存在部分伪射像杂波，需要进一步进行剔除过滤，尽管会错过不少真实射线状杂波的选入，但可以确保极大概率剩下真实的射线状杂波。

根据单站产品数据文件分析，射线状杂波的周边能量值一般不超过1。设计基于当前射线状杂波扫描线为基准，统计与周边扫描线的相关性,如强相关性、T-值分布等[6]，进行进一步滤除。

以当前射线状杂波所在扫描线为基准(称为：基准线)，按扫描方位角前后设定相关统计窗口(窗口内的扫描线称为：窗口线)，窗口数记为W。

（1）强相关性统计。

用来做两条扫描线的相关性检测。强相关系数越大，表明两者之间的相似性越强。

计算基准线与窗口线的强相关系数：

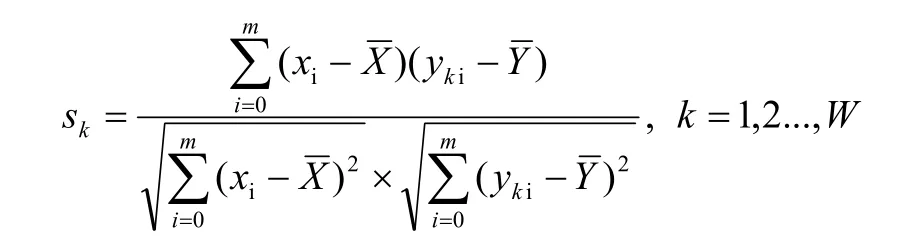
其中xi为基准线上的射线状杂波段的数据，m为该杂波段数据的长度（即点数），为该段数据的均值。yki为第k个窗口线上的对应基准线扫描距的数据，为相应的均值。

这样得到W个强相关系数Sk。

（2）T-值检测。

用来做两条扫描线的显著性差异检测，T-值越大，表明两者之间的关系越小。

这样得到W个T-值系数kT。

根据上述统计分析得到的两种检测标准，我们用于检测基准线是否为符合一定检测水平的射线状杂波，另一方面可以识别窗口线是否可以归类到射线状杂波。

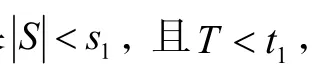
检验水平门限值的选定统计如图2、图3所示。图2中，横轴为强相关系数门限范围[0-1]，按0.1刻度放大10倍，纵轴为符合检测标准的射线数，总共统计6757条疑似射线数，实际射线数7条。可见s0取值越大，检测门槛就越低，当s0=1时，有970条通过检测。s0取值越小，检测门槛越高，当s0=0时，疑似射线全部排除。

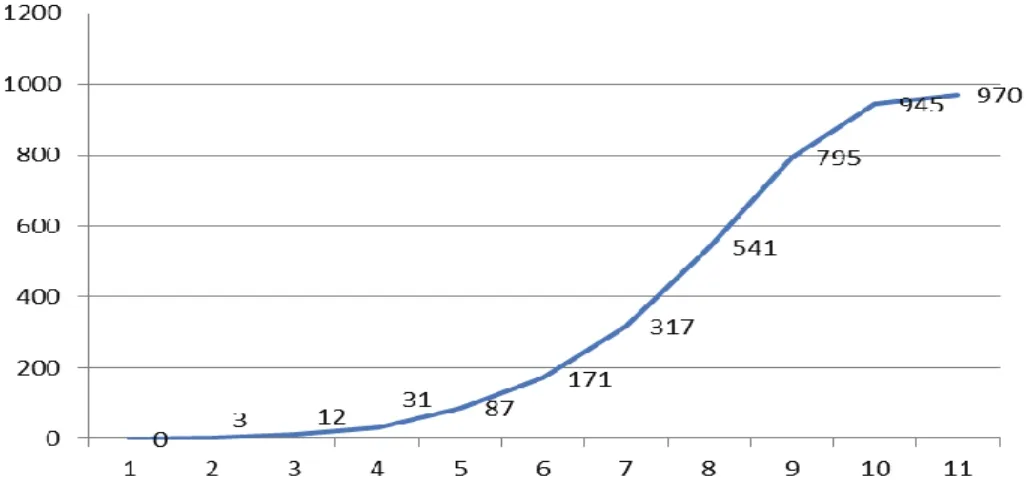
图2 S-检验水平门限值统计图

图3中，横轴为T-值门限范围[0-10]，按0.5刻度放大2倍，纵轴为符合检测标准的射线数，总共统计6757条疑似射线数，实际射线数7条。可见t0取值越大，检测门槛就越高，t0≥4，疑似射线全部排除；t0取值越小，检测门槛越低，当t0=0时，有2326条通过检测。

图3 T-检验水平门限值统计图

综合实际射线数，以及上述两种检测门限的趋势，取s0=0.2，t0=3.0，可以大概率剔除伪射线状杂波。

同理统计分析后，我们取s1=0.6，t0=7.0，可以显著判定相邻的窗口线是否属于射线状杂波。

2.3 杂波抑制的逐点判决方法

对于一个单站雷达产品文件，通过上文所提供的算法计算后，可以大概率找到射线状杂波回波扫描线。如前所述，我们可以定位出射线状杂波的位置和长度，为尽量避免可能有用的回波数据，采用逐点判决。

假设xi（i=1,m）为基准线上的杂波点能量值，以xi为中心点，设定一个7×7的网格窗口，如果窗口内的（除中心点）点yijk的平均值低于中心点到一定阈值时，则将该中心点能量值置为0。移动窗口遍历基准线上的m个杂波点，从而实现杂波的抑制：

Pi越小，表明剔除中心点的可能性越大。

实验表明，一般取0.5作为Pi的判别阈值。当Pi<0.5时，中心点可剔除（能量值置为0），否则我们保留该点数据。

3 实际应用效果

上述算法应用到实际雷达拼图处理中，有效地对射线状杂波进行了抑制，在减少了一些射线状回波对短临预报的干扰方面有一定作用（图4，图5）。此外，该方法还能抑制2016年9月出现的一次“饼图”现象（图6）。

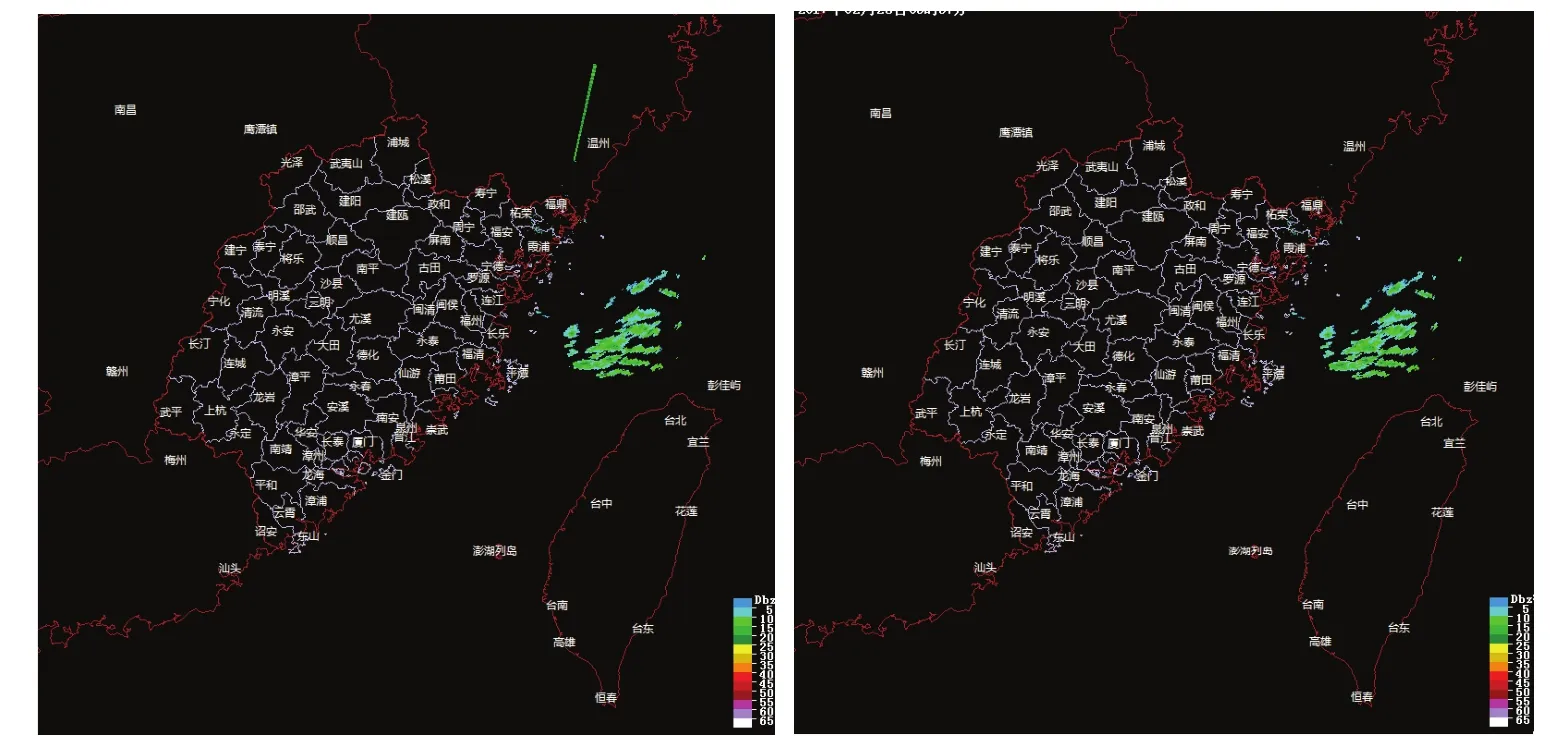
图4 射线状回波抑制前后对比实况1

图5 射线状回波抑制前后对比实况2

图6 一次抑制“饼图”现象的前后对比

4 结论

射线状杂波的抑制想法主要来源于工作中发现诸类现象不少，且或多或少在短临预报、气象服务等方面存在一定的影响，目前也确实没有完全能够抑制的方法，基于尽量发现，准确抑制的想法，经过大量数据分析及实验验证，试图寻找一些技术方法来达成该目标。

目前设计的抑制算法能有效识别并剔除射线状杂波。但算法在实际应用过程中，还存在一些难以定位的射线状杂波，现有的做法是不对其进行抑制处理。此外对这些射线杂波，经过分析，如果一些检验标准放宽些，可以很容易寻找到，但同时也会带来负面影响，导致一些非射线状的杂波被误判，因此算法还有很大的改进空间，如设计更多的检验算法，设计更灵活、能自适应的检验标准，引入其他气象观测数据作为参照等等。

此外，本算法适用于射线状杂波的抑制，也为对于地物回波、鸟群干扰等非天气现象回波方面的研究提供了一种参考思路，即从数据自身出发，研究其特征与非天气现象回波的关联性，从而提出一些假设检验标准。

[1] 俞小鼎,姚秀萍, 熊廷南, 等. 多普勒天气雷达原理与业务应用[M]. 北京：气象出版社, 2006.

[2] 陈媛, 陈江民, 王紫阳, 等. 天气雷达反射率基数据质量控制的几种算法[J].天气与减灾研究, 2007,30(3): 48-51.

[3] 马中元.CINRAD雷达数据质量控制方法初探[J]. 气象. 2010,36(8): 134-141.

[4] Waldteufel P，Corbin H. On the analysis of single-doppler radar data[J]. Journal of Applied Meteorology, 1979, 18(4):532-542.

[5] Meng Z. Methods for improving data quality for WSR-98D weather radar[J]. Meteorological Science & Technology, 2006, 34(21): 85-89.

[6] 梁之舜,邓集贤, 杨维权. 概率论与数理统计[M].北京: 高等教育出版社,1992.