子午线弧长的计算方法及精度分析

刘学杰，杨丽坤

(1. 河南省中纬测绘规划信息工程有限公司，河南 焦作 454000； 2. 郑州工业贸易学校，河南 郑州 450007)

子午线弧长的计算方法及精度分析

刘学杰1，杨丽坤2

(1. 河南省中纬测绘规划信息工程有限公司，河南 焦作 454000； 2. 郑州工业贸易学校，河南 郑州 450007)

计算子午线弧长除了采用经典的级数展开算法之外，还可通过数值积分与常微分方程数值解法进行求解。为评价各种算法的精度，本文选取大地纬度自0°—90°、间隔距离为1°、1′、1″的3组样本数据，分别基于传统算法、数值积分算法和常微分方程数值算法3大类11种算法计算得到各组样本所对应的子午线弧长结果，并从算法精度和运算速度两个方面对各种数值算法进行了分析与评价。实例表明三阶、四阶Runge-Kutta算法不仅精度高，而且运算效率是其他算法的2倍多，研究结果为计算子午线弧长的提供了有效的算法模型。

子午线弧长；数值积分；常微分方程；展开算法

计算子午线弧长是椭球大地测量学的一项基本内容，是高斯-克吕格投影坐标正算的基础问题。子午线弧长的计算公式本质上是一个椭圆函数积分公式，由于被积函数的原函数无法用初等函数的形式予以表示，因此无法得到严格的解析结果。传统做法是基于二项式定理将被积函数展开为级数形式，通过分项积分得到近似的解析结果。

近年来，国内外相关学者对此问题提出了一些新的算法，文献[1—5]基于第二类椭圆积分，将子午线弧长公式表达为有理函数和第二类椭圆积分之和等两类形式不同但结果等价的公式，或是引入椭球的第三扁率和高斯超几何函数，给出解算公式的简化形式，完善了子午线弧长计算方法。文献[6]给出了以空间直角坐标为参数的子午线弧长计算公式。文献[7—8]给出了子午线弧长计算公式的直接展开式。文献[9]基于递归关系给出了任意精度的子午线弧长计算公式，可满足不同精度要求。文献[10]基于数值积分算法对子午线弧长进行了计算，但结果表明数值积分算法与传统级数展开算法存在较大差异。文献[11]利用复合Simpson积分公式表明数值积分算法与传统级数展开算法结果基本一致。

子午线弧长计算公式直观而言是一个椭圆函数积分问题，但其实也是一个标准的一阶常微分方程求解问题。现代数值分析对于这两个数学问题有着成熟的解算方法，前者通过数值积分予以解决，后者则基于常微分方程数值解法进行解算，两类方法的计算过程中都没有涉及深奥的数学理论知识，有完备的算法及公式，程序设计简单易行。本文利用这两类方法对子午线弧长进行了求解，并分析比较了各种算法的精度及运算速度，对算法质量进行了比较与评价。

1 计算子午线弧长的三类算法

1.1 级数展开算法

根据椭球大地测量中曲线弧长与曲率半径的基本关系[12]，子午线上某点P从赤道到该点的子午线弧长X与点P的大地纬度B之间满足如下微分关系

(1)

式中，a、e、M分别为椭球的长半径、第一偏心率、子午线曲率半径。则有

(2)

式(2)无法直接用定积分进行求解，因为被积函数M的原函数无法用初等函数形式进行表达。传统做法是将被积函数M按照二项式定理展开为sin2B的幂级数，并将sinB偶次幂函数按照三角函数的倍角公式展开为余弦的倍数函数，转换为可积函数，然后逐项进行积分。考虑到计算结果目的和精度要求，截断之后得到以下实用计算公式

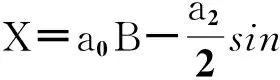
(3)

(4)

(5)

对于我国常用的4个椭球(克拉索夫斯基椭球、IUGG-75椭球、WGS-84椭球、CGCS2000椭球)而言，式(3)最后一项的最大值均未超过0.03 mm，因此截断误差不超过0.1 mm，完全满足测量工作的精度要求。

1.2 数值积分算法

子午线弧长公式本质上是一个椭圆函数的积分问题，可采用数值积分直接进行求解。数值积分有诸如复合梯形算法、复合Simpson算法、Romberg算法、Gauss-Legendre算法、Monte Carlo算法等几种成熟的算法[13～14]，但计算精度与效率各不相同，需要进行分析与比较。

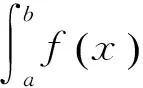
(6)

复合Simpson算法公式为

(7)

Romberg算法公式为

(8)

Gauss-Legendre算法公式为

(9)

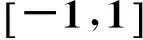
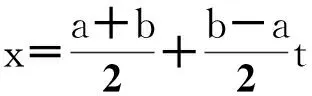
(10)

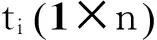
(11)

1.3 常微分方程数值解法

标准的一阶常微分方程形式为

(12)

子午线弧长计算公式本质上即为一个标准的一阶常微分方程，结合椭球实际，式(1)可写为如下形式

(13)

对于式(12)的标准一阶常微分方程，常用的数值计算方法主要有Euler算法、改进的Euler算法，以及二阶、三阶、四阶Runge-Kutta算法[13-14]。

(14)

改进的Euler算法公式为

(15)

二阶Runge-Kutta算法又称为变形的Euler算法，其公式为

(16)

三阶的Runge-Kutta算法公式为

(17)

四阶的Runge-Kutta算法公式为

(18)

2 计算结果分析与评价

为分析对比上述3大类11种算法的计算精度与运算效率，本文以2000国家大地坐标系的椭球基准CGCS2000椭球(a=6 378 137 m、f=1/298.257 222 101、e2=2f-f2)为例，选择了3组大地纬度的样本数据，分别计算得到了各组样本相应的结果，并统计了相应的计算时间(见表1)。

表1 3组大地纬度样本数据基本情况

基于Matlab平台[15]，根据式(3)—式(18)分别对上述3大类11种算法予以编程实现。在对3组样本数据计算过程中，当数值算法程序涉及区间等分数n与步长h时，需要相应样本数据中的样本数目和间隔距离保持一致。

根据各种算法计算得到3组样本数据的子午线弧长后，将同一样本中各种数值算法结果与级数展开算法结果进行求差，差值即可反映各种数值算法的精度情况，具体结果见表2。

采用Monte Carlo算法，3组样本中差值的最大值分别达到4998、1670和301 m，表明该算法结果错误，表2中不再列出具体数值。对于Gauss-Legendre算法，分别计算了二阶、三阶、四阶、五阶的计算结果，其中二阶、三阶、四阶计算精度较差，因此表2中仅给出了五阶算法的计算结果。对于Romberg算法，计算限差取10-5(对应计算结果截至0.01 mm)。

各种算法的运算速度也是衡量算法有效性的一个重要指标，现将3组样本中各种数值算法的计算时间列于表2中。其中第1—2组样本中传统算法的计算耗时均未超过1 s，第3组样本中传统算法的计算耗时为458 s。

从表2可以看出，在算法的计算精度方面，只有Romberg算法和三阶、四阶的Runge-Kutta算法的计算结果与传统展开算法结果间的差值在0.1 mm以内，能够满足测量工作的需要；而复合梯形算法、复合Simpson算法、Euler算法、改进的Euler算法及二阶的Runge-Kutta算法，随着步长h的缩小、区间等分点n的增多，计算精度随之提高，但Euler算法直至步长h=1″差值仍大于155 mm，由此可知这些算法精度不能满足测量工作的需要。Gauss-Legendre算法结果精度与步长、等分点数无关，计算精度仅随阶数的增大而提高。

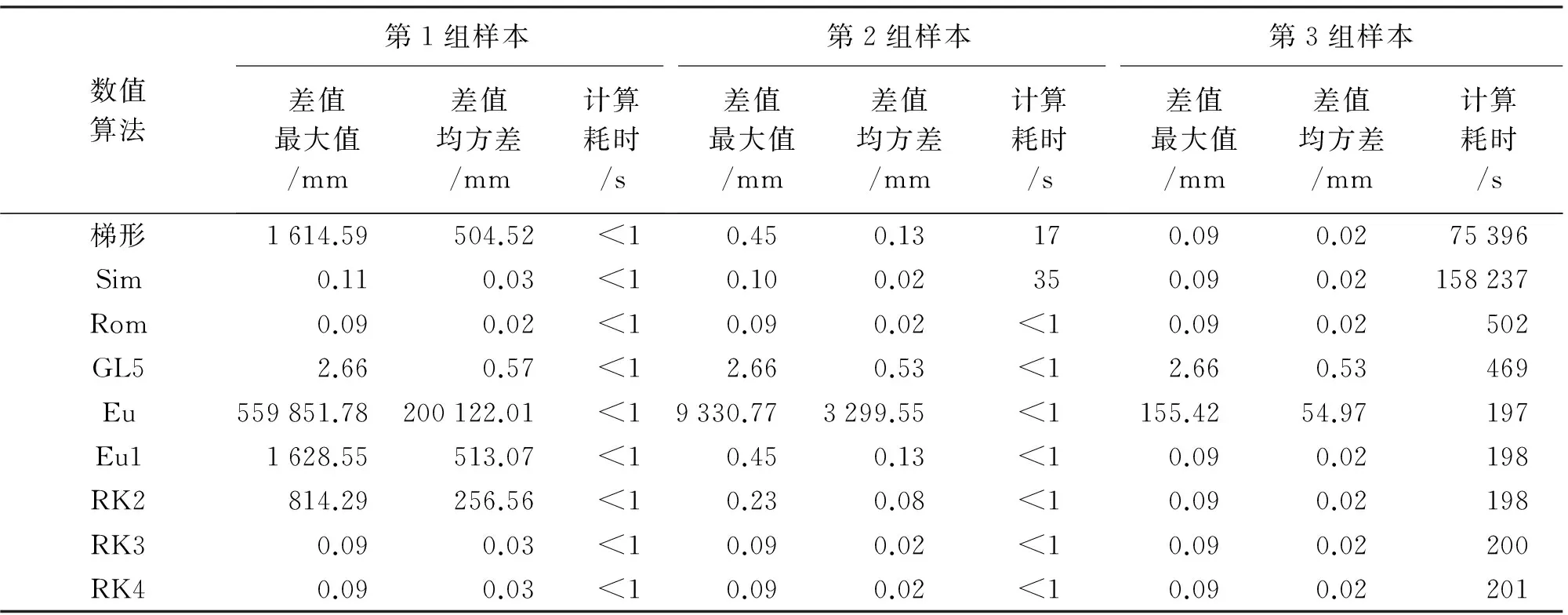
表2 各种数值算法与传统算法结果间差值及数值算法计算耗时统计

注：表2第一列中的梯形、Sim、Rom、GL5、Eu、Eu1、RK2、RK3、RK4分别代表复合梯形、复合Simpson、Romberg、五阶Gauss-Legendre、Euler、改进Euler、二阶Runge-Kutta、三阶Runge-Kutta、四阶Runge-Kutta算法。

在算法的运算速度方面，由于第1组和第2组样本数目较少，各种算法的计算耗时基本都在1 s之内，难以反映出算法的效率，但从第2组样本的计算耗时可以看出复合梯形、复合Simpson算法的运算速度要明显慢于其他几种算法。第3组样本数目多达324 001个，各种数值算法的运算速度可以非常清晰区分开来：Romberg算法、Gauss-Legendre算法的运算速度与传统算法大体相当；传统算法速度分别是复合梯形算法、复合Simpson算法的165倍和345倍，这两种数值算法速度最慢，不适用于大数据的计算；而常微分方程的5种数值解法运算速度大致相同，均为传统算法速度的2倍多。

综合3组样本数据各种数值算法结果精度与运算速度两方面因素，三阶、四阶的Runge-Kutta算法最优，不仅计算精度高，而且运算速度是传统算法的2倍多，优于其他几种数值积分算法。而复合梯形算法、复合Simpson算法虽然可以通过减小步长及增大区间等分点数来提高计算结果的精度，但运算速度却急剧降低。

3 结 语

本文基于传统的展开算法、数值积分和常微分方程数值解法分别对子午线弧长进行了计算，并从计算精度、运算速度两个方面对各种算法的有效性进行了分析与评价。试验结果表明，采用常微分方程数值解法比传统算法速度快、精度高；而数值积分虽然可以通过减小步长来提高结果精度，但计算速度低，难以适用于大数据计算。本文研究结果为计算子午线弧长提供了一条新的途径和借鉴。

[2] DORRER E.From Elliptic Arc Length to Gauss-Kruger Coordinates by Analytical Continuation[C]∥Geodesy: The Challenge of the 3rd Millennium. Berlin: Springer, 2003: 293-298.

[3] KAWAS K.A General Formula for Calculating Meridian Arc Length and Its Application to Coordinate Conversion in the Gauss-Kruger Projection [J]. Bulletin of the Geospatial Information Authority of Japan, 2011, 59(2):1-13.

[4] 过家春，赵秀侠，徐丽，等．基于第二类椭圆积分的子午线弧长公式变换及解算[J]．大地测量与地球动力学，2011，31(4)：94-98．

[5] 过家春．子午线弧长公式的简化及其泰勒级数解释[J]．测绘学报，2014，43(2)：125-130．

[6] 牛卓立．以空间直角坐标为参数的子午线弧长计算公式[J]．测绘通报，2001(11)：14-15．

[7] 严伯铎．椭球子午线弧长的一种计算方法[J]．地矿测绘，2003，19(3)：7-10．

[8] 李厚朴，刘敏，孔海英，等．子午线弧长和等面积纬度函数变换的直接展开式[J]．海洋测绘，2011，31(1)：17-19．

[9] 刘仁钊，伍吉仓．任意精度的子午线弧长递归计算[J]．大地测量与地球动力学，2007，27(5)：59-62.

[10] 刘修善．计算子午线弧长的数值积分法[J]．测绘通报，2006(5)：4-6．[11] 杨双富．再议计算子午线弧长的数值积分法[J]．城市勘测，2010(6)：140-142．

[12] 孔祥元，郭际明，刘宗泉．大地测量学基础[M]．武汉：武汉大学出版社，2007：106-116．

[13] 李庆扬，王能超，易大义．数值分析 [M]．4版．北京：清华大学出版社，2001：336-359．

[14] 易大义，沈云宝，李有法．计算方法[M]．杭州：浙江大学出版社，2000：243-266．

[15] 宋叶志，贾东永．MATLAB数值分析与应用[M]．北京：机械工业出版社，2010：380-410．

Calculation Methods and Accuracy Analysis of Meridian Arc Length

LIU Xuejie1，YANG Likun2

(1. Zhongwei Surveying and Planning Information Engineering Co.,Ltd. of Henan Province, Jiaozuo 454000，China;2. Zhengzhou Industry and Trade School, Zhengzhou 450007，China)

There are several kinds of algorithms for calculating the meridian arc length except the classical expanded algorithm, such as numerical integration and ordinary differential equations numerical solution. In order to study the accuracy of each algorithm, this paper selected 3 sets of sample data within the geodetic latitude from 0° to 90°, whose intervals are 1°,1′,1″, respectively. Based on the traditional expanded algorithms, numerical integral algorithms and numerical solution of ordinary differential equations, the corresponding meridian arc length results were calculated and the quality of each numerical algorithm with regard to algorithm accuracy and computation speed were evaluated. The results show that the 3 and 4 order Runge-Kutta algorithm not only have high precision but the computing speed is twice more than other algorithms. This paper provides new, reliable algorithm with high speed for meridian arc length calculation. The results provide an effective algorithm for calculating the meridian arc length.

meridian arc length; numerical integral; ordinary differential equations; expanded algorithm

刘学杰，杨丽坤.子午线弧长的计算方法及精度分析[J].测绘通报，2017(8)：106-109.

10.13474/j.cnki.11-2246.2017.0264.

2017-02-20

2016年国家重点研发计划(2016YFC0803103)；河南省高校创新团队支持计划(14IRTSTHN026)；河南省创新型科技创新团队支持计划

刘学杰(1968—)，男，高级工程师，主要研究方向为测绘科学与技术。E-mail：zwchlxj@126.com

P226

A

0494-0911(2017)08-0106-04