基于内环H∞控制的实时混合试验
宁西占, 周惠蒙, 吴 斌, 王 贞
(1.哈尔滨工业大学 结构工程灾变与控制教育部重点实验室,哈尔滨 150090;2.哈尔滨工业大学 土木工程学院,哈尔滨 150090;3.中国地震局工程力学研究所地震工程与工程振动重点实验室,哈尔滨 150080)
基于内环H∞控制的实时混合试验
宁西占1,2, 周惠蒙3, 吴 斌1,2, 王 贞1,2
(1.哈尔滨工业大学 结构工程灾变与控制教育部重点实验室,哈尔滨 150090;2.哈尔滨工业大学 土木工程学院,哈尔滨 150090;3.中国地震局工程力学研究所地震工程与工程振动重点实验室,哈尔滨 150080)
实时混合试验将结构的关键部位作为试验子结构进行试验,而其余部分作为数值子结构在计算机中模拟,并通过作动器或振动台对试验子结构进行加载来实现二者边界条件的协调。由于作动器-试件系统复杂的非线性动力特性,传统的PID控制器性能受到一定影响,必须采用时滞补偿方法或外环控制消除作动器-试件系统的非线性动力特性影响,才能保证实时混合试验的成功。为在作动器内环消除作动器-试件系统非线性动力特性的影响,采用基于混合灵敏度的H∞控制理论设计实时混合试验作动器内环控制器,并研究了这种方法的可行性。数值仿真表明,H∞控制器表现出较好的跟踪性能并具有一定的鲁棒性;单自由度线弹性结构实时混合试验证明了该方法在作动器内环控制上的可行性。
实时混合试验;内环控制;H∞控制;鲁棒性;混合灵敏度
实时混合试验由拟动力试验发展而来[1],它可以对具有速度或加速度相关特性的结构或构件进行试验,在工程抗震试验领域得到了不断的研究。实时混合试验的关键在于数值子结构与试验子结构在边界处运动量的协调和力的平衡。然而作动器-试件系统复杂的非线性动力特性使作动器难以在积分时间末准确实现期望位移,这将带来试验误差,使试验精确性降低甚至发散,从而导致实时混合试验失效。因此,品质优良的控制方法成为实时混合试验成功的必要条件。Wagg等[2]在实时混合试验中采用了最小控制合成法(Minimal Controller Syn-thesis,MCS),试验结果表明该方法可行,由于其试验子结构质量太小,这种方法对土木工程结构试验的适用性有待研究;Stoten等[3]提出了最小合成误差反馈控制法,该控制方法对结构参数变化、试件非线性仍具有较好效果;Phillips等[4]提出了基于模型的前馈反馈控制方法,其控制效果与模型的准确程度有关,作动器模型不宜高于三阶;Wu等[5]将滑动模态控制方法代替比例积分(Proportional Integral Controller,PI)和比例微分(Proportional Differential,PD)控制应用于实时混合试验的等效力控制方法中,通过对弹簧试件和防屈曲支撑试件的研究表明滑动模态控制方法具有较好的控制效果。
自1981年Zames[6]提出H∞控制思想以来,该方法得到了广泛的研究。它在设计过程中考虑了建模的不确定性、参数不确定性和外界干扰的影响,具有很好的鲁棒性,且兼顾了频域方法的形象与时域方法的灵活等特点。徐洋等[7]采用H∞方法对AMD(Active Mass Driver)结构主动控制中的Benchmark问题进行了研究,并通过数值仿真表明该方法具有较好的鲁棒性。Gao[8]在作动器内环控制基础上基于回路成型设计了H∞外环控制器并应用于实时混合试验,通过钢框架试验证明该方法具有很好的鲁棒性与跟踪性能,但却存在稳态误差。
本文研究了实时混合试验内环作动器H∞控制方法,从作动器内环消除作动器-试件系统的非线性特性带来的试验误差和潜在稳定性问题。将基于混合灵敏度的H∞控制方法应用于实时混合试验中作动器-试件系统的加载控制,通过加权函数来考虑作动器-试件系统的不确定性。结合特定算例,对权函数的选取以及控制器的设计方法作出了详细阐述。数值仿真和实时混合试验证明了H∞控制方法在实时混合试验中的可行性。
1 H∞控制方法原理
H∞控制是通过建立所关心的性能指标并以其H∞范数作为衡量标准,通过不断优化该性能指标来设计控制器的方法。图1给出了标准H∞控制问题的一般框图,其中G表示性能加权的广义被控对象,K为所需设计的控制器,w为包含参考输入、干扰等的广义输入,u为控制输入,z为性能输出,y为控制输出。

图1 标准H∞控制框图
标准H∞控制问题可通过一般的反馈控制问题经性能加权获得,如图2所示,其中P为被控对象,K为所需设计控制器,w为参考输入,WS、WR和WT分别为性能加权矩阵。权函数WS、WR和WT分别反应了系统的追踪性能、控制器输出性能和模型的不确定性,于是得到输入(w,u)到输出(z,y)的传递函数,即广义被控对象为
(1)
式中:0和I分别为具有相应维数的零矩阵和单位矩阵。其状态空间实现表示为
z=C1x+D11w+D12u
y=C2x+D21w+D22u
(2)
式中:x是状态向量(本文为位移及其对时间的各阶导数),“·”表示状态向量对时间的一阶微分;A是状态转移矩阵,B1和B2是输入位置矩阵,C1和C2是输出矩阵,D11、D12、D21和D22是直接传输矩阵。从而广义被控系统可记为
(3)
采用DGKF法[9]设计H∞控制器,就是寻求一个使得系统内稳定的控制器K,并使广义输入w到性能输出z的闭环系统的线性分式变换FL(G,K)的H∞范数小于γ,γ为给定的正数。FL(G,K)的表达式为
FL(G,K)=G11+G12K(I-G22K)-1G21
(4)

图2 加权的反馈控制框图
若式(2)所示广义被控对象满足以下条件:
(1) (A,B2)为可镇定的,(C2,A)为可检测的;
(2)D12=[0;I]、D21=[0I];
其中,ω是频率,j是虚数单位,则可基于2个Riccati方程并通过DGKF法[9]来设计H∞控制器。
定义系统的灵敏度函数、控制器灵敏度函数和补灵敏度函数分别为
S=(1+PK)-1
(5)
R=K(1+PK)-1
(6)
T=I-S=PK(1+PK)-1
(7)
灵敏度函数S反映了系统的开环变化对闭环性能的影响程度,是参考输入w到误差信号e的传递函数;补灵敏度函数T反映了响应信号对命令信号的跟踪性能,是系统的参考输入w到测量输出y的传递函数;控制器灵敏度函数R可以看作是系统的参考输入w到控制器输出u的传递函数。因此,调整权函数WS可改善系统的跟踪特性以及对干扰的抑制能力,调整权函数WR可避免控制输出过大甚至饱和,而调整权函数WT则可保证被控系统对高频输入具有较好的鲁棒性。权函数选取原则可参考文献[10]。
2 控制器设计
2.1 控制对象
本节将阐述基于混合灵敏度的H∞控制器设计过程。这里将作动器-试件系统称之为内环,采用H∞控制理论设计实时混合试验内环H∞控制器,如图3所示,图中RN、RE、dN、dE、d、dc、rm分别为数值子结构恢复

(a) 实时混合试验流程图

(b) 作动器-试件系统
力、试验子结构恢复力、数值子结构位移、试验子结构位移、测量位移、作动器位移命令和作动器出力。采用文献[11]中电液伺服系统建模方法,通过对电液伺服系统的各个环节进行线性简化,结合电液伺服系统出厂指标以及油压(见表1)等信息获取被控对象模型。得到简化的从控制输入u到位移输出d的传递函数表达式为
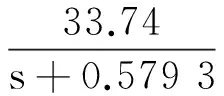
(8)
2.2 权函数选择
实时混合试验中不仅要求作动器在积分时间末能够实现对命令信号的追踪,而且要避免发送给伺服阀的电压过大而造成流量饱和,同时控制器应能考虑到系统的不确定性,因此控制器设计问题为S/R/T混合灵敏度问题。

表1 电液伺服系统相关技术指标
权函数WT与被控对象建模的不确定性有关,反应了标称模型(被控对象P)与实际模型未建模高频动态特性的差异,文献[7,10]给出了其选取方法。为加速系统频响函数在高频处的衰减以达到对高频噪声的抑制,本文选取权函数WT使其具有s2特性。由传递函数的性质可知,广义被控对象G应为有理真分式,因此选择权函数WT使其在所考察的频率范围内具有近似s2特性。经试算,其表达式为
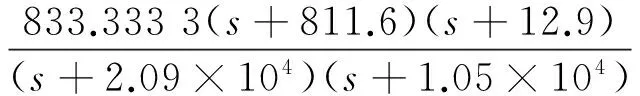
(9)
权函数WS与系统的追踪能力有关,直接影响着被控后系统的动态性能。选择权函数WS使系统在所关心的频率范围内具有较小的灵敏度增益,同时为避免被控后系统出现稳态误差,应使权函数WS应具有积分特性。经试算,其表达式为

(10)
从图4可以看出,权函数WS的穿越频率远小于WT的;权函数WT在低频段奇异值远小于1,且随着频率的增加而逐渐变大,当超过某一频率时,奇异值远大于1,在高频处权函数WT具有接近40 dB/dec的斜率,表明其具有近似s2特性;WS的斜率为-20 dB/dec,具有积分特性。
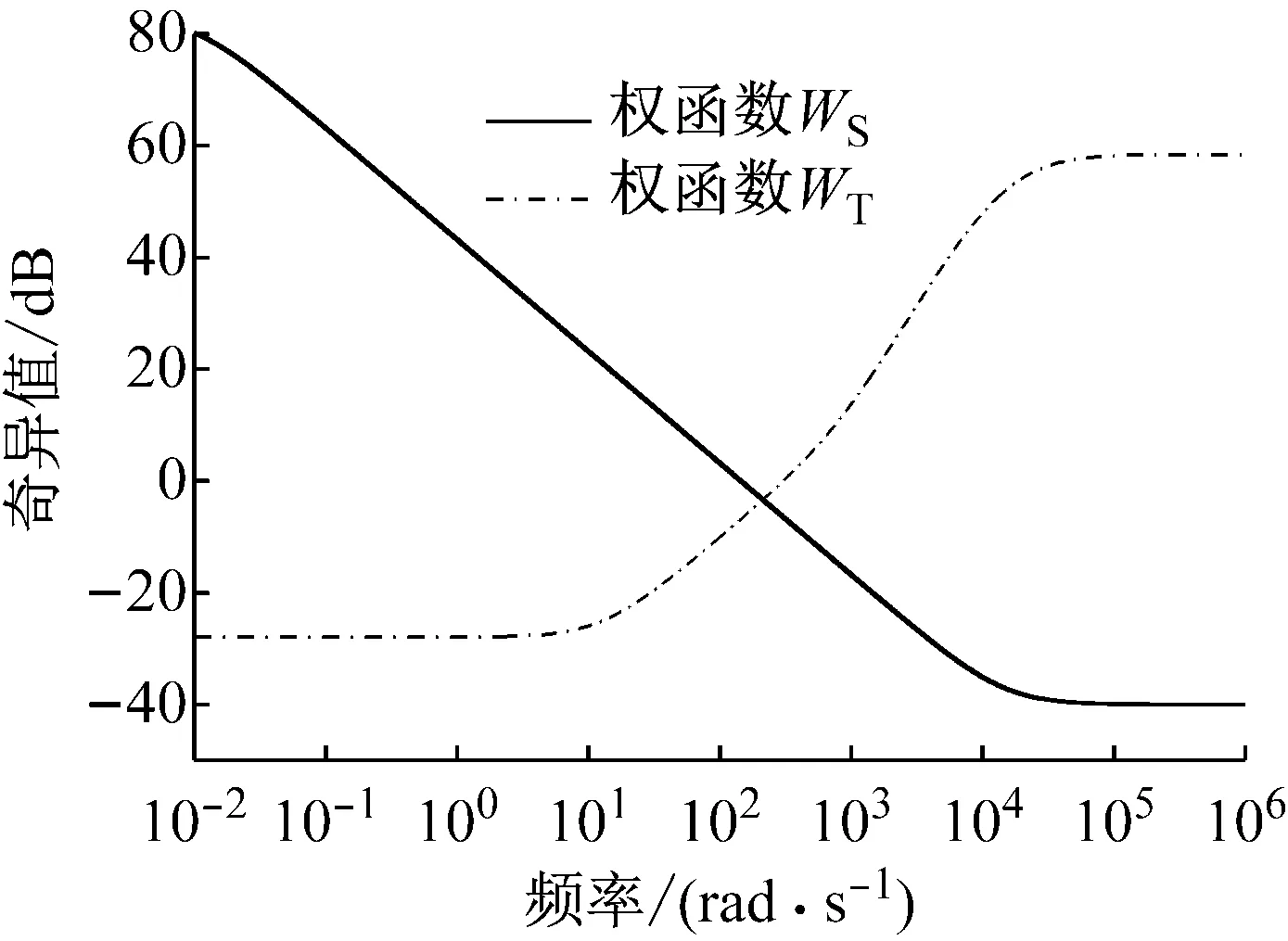
图4 权函数奇异值图
考虑到控制器输出u过大易造成流量饱和,经试算,选取选函数WR为
WR=0.1
(11)
2.3 控制器的获取
权函数选取完成后,借助Matlab鲁棒控制工具箱,将传递函数形式的广义被控对象G(式(4))转化为状态空间形式(式(5)),通过求解Riccati方程进而获取控制器。本文的控制器传递函数表达式为

(12)
3 控制器性能仿真


图5 闭环系统性能图
为考察被控后系统的动态性能,本文采用Matlab/Simulink对被控后系统的单步阶跃响应进行了分析。考虑试验中由于外界振动、A/D和D/A转换以及接口转换等因素,将不可避免的引入噪声,本节分析中也分析了含有测量噪声的单步阶跃响应。需要说明的是,仿真中所施加的测量噪声信号为试验中加载系统开机状态下实测的噪声信号,噪声峰值为0.22 mm。
从图6中可以看出,无噪声时系统达到稳态耗时小于0.02 s且无稳态误差。在有噪声时,系统响应单调上升并趋于稳态,且调节时间小于0.02 s;存在超调现象,但超调量为2%,在可接受的范围内。同时可以看出,两种工况下系统的上升时间和调节时间相同,控制器表现出一定的鲁棒性能。
同时,为考察所设计控制器在应用于实时混合试验时的性能,完成了单自由度线弹性结构的虚拟实时混合试验仿真,计算简图如图7所示。结构阻尼比ζ=0.1,周期T=2 s;数值子结构质量MN=6 889.8 kg,刚度KN=34 N/mm;试验子结构为质量、阻尼可忽略不计的线性弹簧试件,刚度为KE=34 N/mm。选用的地震动为EI Centro(NS,1940) 地震加速度记录,峰值加速度为80 gal。数值积分算法为中心差分法,积分步长为0.02 s,系统采样频率为1 000 Hz。仿真在Matlab/Simulink中完成。同时,采用Matlab软件中的LSIM命令计算得到位移时程作为参考解。

图6 有无系统噪声下阶跃响应

图7 单自由度结构计算简图
虚拟实时混合试验的模拟结果如图8所示。从图8(a)可以看出,作动器响应与作动器命令完全重合,作动器响应与参考解基本吻合;从图8(b)可以看出,在积分时间末点,作动器响应能够完全跟踪作动器命令,无超调现象,且能与参考解吻合良好。算例表明,设计H∞控制器作为实时混合试验作动器内环控制器是可行性的。
4 试验验证
本试验在哈尔滨工业大学力学与结构试验中心进行,所用电液伺服作动器为FTS,由北京富力通达技术有限公司生产;控制器采用dSPACE系统,硬件控制板为DS1104。试验中位移传感器为德国NOVOTECHNIK公司生产的型号为LWH-200的位移传感器,最大量程为200 mm;力传感器是由Vishay公司生产的PSD-5tSJTT传感器,最大量程为5 t;伺服阀是由MOOG公司生产的型号为MOOG-761-3005伺服阀。试验装置如图9。鉴于试验系统加载条件的限制,选用弹簧试件作为试验子结构,并采取轴向加载。图10和图11分别给出了试验系统的测量噪声和一阶作动器数值模型与试验识别模型(扫频信号)的对比图。从图10中可以看出,试验系统具有较大的测量噪声,且从图11中可以看出设计控制器所用数值模型与真实系统具有较大的差异。为此本文主要探讨H∞控制器在较大测量噪声和模型不确定性情况下的性能。需要说明的是,在进行试验前将弹簧预拉50 mm,以保证试验过程中弹簧处于受拉状态。此时,测得的弹簧刚度为35 N/mm。
(a) 整体图

(b) 局部放大图
4.1 系统验证
试验系统模型如式(8)所示,考虑到真实系统与理论模型的差别,经试算,权函数如式(13)所示,于是得到用于真实试验时的控制器表达式如式(14)所示。

图9 试验装置照片

(a) 测量力噪声
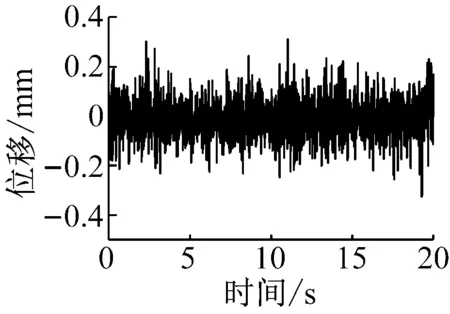
(b) 测量位移噪声
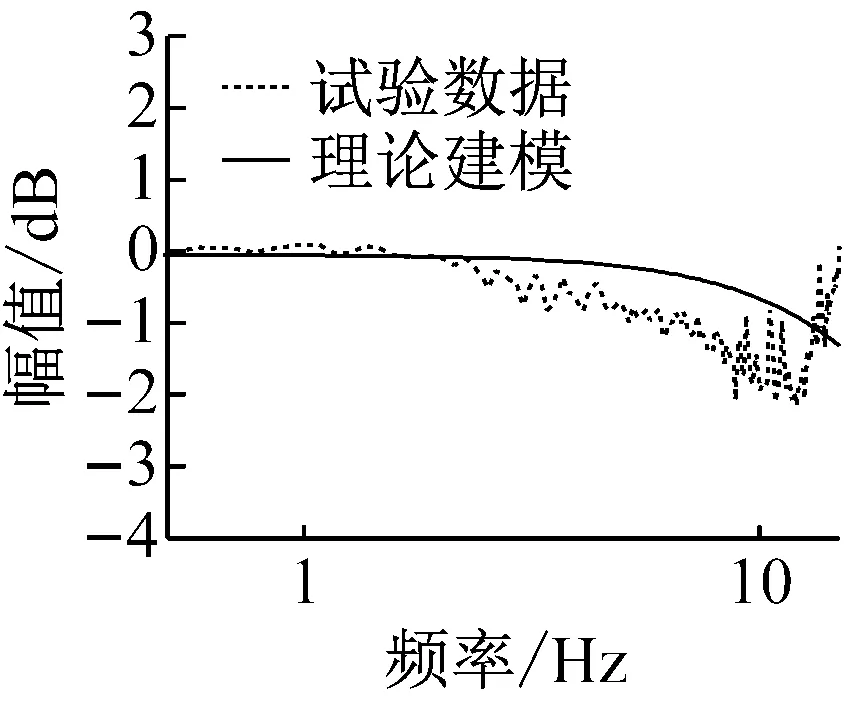
(a) 幅值

(b) 相位

WR=1×10-6
(13)

(14)
由于试验系统为数字采样系统,试验前采用Matlab中c2d命令将控制器连续状态表达式转化为离散形式,离散步长为0.001 s,离散方法为Tustin。为削弱测量噪声对试验的影响,试验中使用了最小阶Elliptic滤波器对力和位移信号进行了滤波。滤波器采样频率为1 000 Hz,对位移滤波的截止频率为100 Hz,对测量力滤波的截止频率为30 Hz。完成了幅值为2 mm,频率分别为f=0.5 Hz和f=5 Hz的正弦荷载激励试验,以验证系统性能,试验结果如图12所示,值得说明的是这个实验仅有内环控制,没有数值计算部分。
从图12中可以看出,当激励频率为0.5 Hz时,作动器响应与命令吻合良好;当激励频率增加到5 Hz时,作动器响应与命令间存在一定的滞后,平均滞后量约0.008 s,远小于积分步长。可见,所设计控制器可保证实时混合试验的顺利进行。

(a) f=0.5 Hz
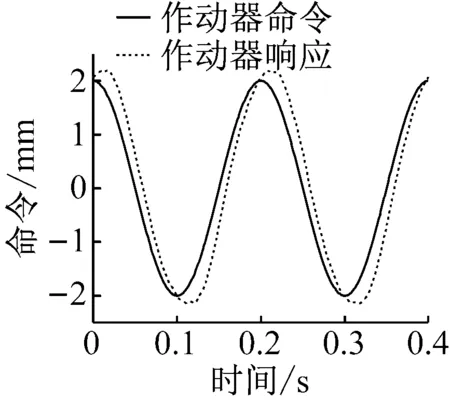
(b) f=5 Hz
4.2 实时混合试验
完成了单自由度实时混合试验,计算简图如图7所示。其中试验子结构刚度为KE=35 N/mm,数值子结构刚度为KN=35 N/mm,结构阻尼比为ζ=0.1,结构周期为T=2 s。数值积分方法为中心差分法,积分步长为0.02 s。试验中滤波器参数设置与4.1节相同。为验证实时混合试验结果的正确性,采用Matlab软件中的LSIM命令计算得到位移时程作为参考解。
(1) 正弦激励
所选正弦荷载的周期为0.5 s,力幅值由0慢慢增至344.492 N,其稳态响应如图13所示。

(a) 稳态响应整体

(b) 局放大部图
从图13(a)可以看出,作动器的响应、命令和参考解完全重合;由图13(b)可以看出,在积分时间末,作动器响应跟踪能很好的跟踪上作动器命令,且能与参考解吻合良好,说明在该正弦荷载激励作用下,H∞控制器表现出较好的跟踪效果。
(2) 地震激励
选取地震动为EI Centro(NS,1940)地震加速度记录,峰值加速度为50 gal,加载时长40 s。
从图14(a)位移时程图可以看出,当结构响应达到峰值前,试验结果与参考解吻合良好;随着响应的衰减,试验结果与参考解在波峰和波谷处出现差异;20 s之后,试验结果与参考解吻合良好。从图14(b)局部放大图可以看出,作动器响应与作动器命令基本完全重合,表明所设计H∞控制器能够使作动器很好地实现对命令信号的追踪。

(a) 整体图
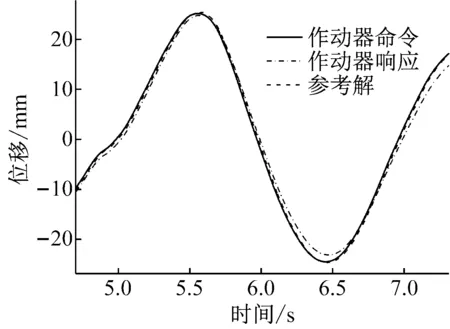
(b) 局部图
为定量评价试验结果,定义如下误差指标

(15)
该误差指标同时考虑了相位误差和幅值误差,反应了系统对信号的再现能力。经计算,作动器的跟踪误差为3.77%,表明H∞控制器具有较好的跟踪性能,可实现对参考输入的完全跟踪;试验结果与参考解的误差为14.69%,表明在内环H∞控制器作用下,实时混合试验可反应结构的真实地震响应。
5 结 论
为消除作动器-试件系统复杂非线性动力特性引起的试验误差和潜在稳定性问题,本文对实时混合试验内环控制进行了探索。采用基于混合灵敏度的H∞控制方法,以线性化作动器-试件模型为控制对象,简述了权函数的选取,设计了实时混合试验内环控制器,详述了控制器性能评判标准。通过有/无噪声的阶跃输入数值模拟,H∞控制器表现出良好的跟踪性能和鲁棒性能;单自由度实时混合试验数值模拟表明,采用内环H∞控制器的作动器在积分步长末能很好的跟踪信号输入。正弦激励和地震激励下单自由度线弹性结构的实时混合试验结果表明:内环采用H∞控制器的作动器能够很好的再现命令信号的幅值和相位,结构位移响应与参考解吻合良好。数值模拟和试验验证表明,基于混合灵敏度的H∞控制方法在作动器内环控制上是可行性的。
[1] NAKASHIMA M, KATO H, TAKAOKA E. Development of real-time pseudo dynamic testing[J]. Earthquake Engineering & Structural Dynamics, 1992, 21(1): 79-92.
[2] WAGG D J, STOTEN D P. Substructuring of dynamical systems via the adaptive minimal control synthesis algorithm[J]. Earthquake Engineering & Structural Dynamics, 2001, 30(6): 865-877.
[3] STOTEN D P, TU J Y, LI G. Synthesis and control of generalized dynamically substructured systems[J]. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 2009, 223(3): 371-392.
[4] PHILLIPS B M, SPENCER JR B F. Model-based feedforward feedback actuator control for real-time hybrid simulation[J]. Journal of Structural Engineering, 2013, 139(7):1205-1214.
[5] WU B, ZHOU H. Sliding mode for equivalent force control in real-time substructure testing[J]. Structural Control and Health Monitoring, 2014, 21(10): 1284-1303.
[6] ZAMES G. Feedback and optimal sensitivity: Model reference transformations, multiplicative seminorms, and approximate inverses[J]. IEEE Transactions on Automatic Control, 1981, 26(2):301-320.
[7] 徐洋, 姜洪洲, 叶正茂, 等.H∞控制在AMD Benchmark结构主动控制中的应用研究[J]. 振动与冲击, 2005, 24(5): 14-17.
XU Yang, JIANG Hongzhou, YE Zhengmao, et al. Research on the application ofH∞control in the MD active structure control benchmark problem[J]. Journal of Vibration and Shock, 2005, 24(5): 14-17.
[8] GAO X, CASTANEDA N, DYKE S J. Real time hybrid simulation: from dynamic system, motion control to experimental error[J]. Earthquake Engineering & Structural Dynamics, 2013, 42(6):815-832.
[9] ZHOU K, DOYLE J C, GLOVER K. Robust and optimal control[M]. New Jersey: Prentice Hall, 1996, 442-445.
[10] 吴旭东, 解学书. H∞鲁棒控制中的加权阵选择[J]. 清华大学学报(自然科学版), 1997, 37(1): 27-30.
WU Xudong, XIE Xueshu. Weighting function matrix selection inH∞robust control[J]. Journal of Tsinghua University (Sci & Tech), 1997, 37(1): 27-30.
[11] 邢宗义, 张媛, 侯远龙, 等. 电液伺服系统的建模方法研究与应用[J]. 系统仿真学报, 2009, 21(6): 1719-1725.
XING Zongyi, ZHANG Yuan, HOU Yuanlong, et al. Modeling of electrohydraulic system and its application[J]. Journal of System Simulation, 2009, 21(6): 1719-1725.
Real-time hybrid simulation based on inner-loopH∞control
NING Xizhan1,2, ZHOU Huimeng3, WU Bin1,2, WANG Zhen1,2
(1. Key Lab of Structures Dynamic Behavior and Control, Harbin Institute of Technology, Ministry of Education, Harbin, 150090, China; 2. School of Civil Engineering, Harbin Institute of Technology, Ministry of Education, Harbin, 150090, China; 3. Key Laboratory of Earthquake Engineering and Engineering Vibration, Institute of Engineering Mechanics, China Earthquake Administration, Harbin, 150080, China)
Real-time hybrid simulation (RTHS) was used to take key parts of a structure as a test substructure for testing, and the remainder of the structure as a numerical substructure for simulation, an actuator or a shaking table was used for loading on the test substructure to realize the boundary condition between the two substructures to be compatible. Owing to the complex nonlinear dynamic characteristics of the actuator-specimen system, the performance of a traditional PID controller was easy to be affected. The time delay compensation or the outer-loop control strategy was used to eliminate the former’s influences to ensure the success of RTHS. TheH∞control theory based on the mixed sensitivity was adopted to design the inner-loop controller of RTHS. Numerical simulations indicated that theH∞controller has an excellent tracking performance and robustness; the RTHS of a linear elastic single-DOF structure verifies the feasibility of the proposed method in actuator inner-loop control.
real-time hybrid simulation (RTHS); inner loop control;H∞control; robustness; mixed sensitivity
中国地震局工程力学研究所基本科研业务费专项项目(2016B09);国家自然科学基金(51161120360;51408565;51408157);高等学校博士学科点专项科研基金(20132302110065)
2016-02-23 修改稿收到日期:2016-06-19
宁西占 男,博士生,1987年12月生
吴斌 男,博士,教授,1970年1月生 E-mail:bin.wu@hit.edu.cn
TU317
A
10.13465/j.cnki.jvs.2017.15.009

