基于最大熵原理的风电场风频分布研究

郁永静,何 一,刘志远,熊万能

(中国电建集团成都勘测设计研究院有限公司,四川成都,610072)

基于最大熵原理的风电场风频分布研究

郁永静,何 一,刘志远,熊万能

(中国电建集团成都勘测设计研究院有限公司,四川成都,610072)

为了研究某风场的风速分布特性及其随高度的变化规律,将威布尔分布和最大熵原理应用于两个测风塔的年风速频率分布拟合中。研究表明,在同一高度上威布尔分布的频率峰值低于实测频率最大值,最大熵分布的频率峰值则与实测非常接近；在不同高度上,随高度的增加,最大熵原理表现出更为明显的优势。从平均有效风能密度来说,五参数最大熵分布计算的误差均值为1.71 W/m2,而威布尔分布的误差均值为7.48 W/m2。

年风频分布；最大熵原理；威布尔分布

风能资源评估是风能开发利用的关键环节,它是制定风能规划、风电场选址和风电功率预测的重要基础,而年风频分布对于风能资源评估起着重要的作用。受地形条件和气象因素的影响,年风频分布函数在不同地区表现出不同的性质。1976年,Wentink[1]将威布尔函数应用于拟合年风频分布,Justus等[2]用威布尔分布对135个气象站的风速分布进行了拟合,均取得了很好的效果。从此,威布尔分布成为拟合年风频分布应用的主流。威布尔分布在零风速时的概率密度为零,明显与事实不符,为解决这个问题,20世纪90年代初,胡文忠等[3]提出了一种四参数混合模型,在低风速段的拟合精度明显高于威布尔分布,但这种方法不便于使用,未成为威布尔分布的替代方法。Deaves和Lines 提出用高风速频率外推的方法来计算低风速段频率[4]。

2005年以来,最大熵原理拟合风频分布成为研究热点,Li Meishen和Li Xiaoguo[5]以熵值最大为准则,拟合了几个测站的风频分布,通过与威布尔分布的对比发现最大熵原理拟合精度较高；此后两位学者拟合了滑铁卢地区小时、月、季和年风频分布,并计算了其对应的风能密度,与实测数据的相关系数都在0.70以上[6]。Ramírez等[7]将最大熵原理应用到三个气象站的风频拟合,认为最大熵原理拟合风频分布可以作为威布尔分布的替代方法。Chellali等[8]借鉴Li Meishen的研究方法对阿尔及利亚地区进行风频拟合,取得了比较好的效果。

研究风场具有高平均风速、低湍流、低风剪切的特性,为研究该区域的风能资源特性,本文将威布尔分布和最大熵原理模型应用于该风电场两个测风塔年风频拟合。

1 威布尔分布

威布尔分布[9]的概率密度函数为

(1)

式中,k为威布尔分布的形状参数,是一个无量纲量,取值在1～3之间,；A为尺度参数,是与平均风速相关的参数,单位为m/s。两参数和平均风速间关系见公式(2)[10]。

(2)

式中,Γ为gamma函数。

早期学者们应用绘图法和最小二乘回归来确定威布尔参数,Seguro和Lambert用最大似然法、修正最大似然法和传统最小二乘回归对威布尔参数进行估计,得出似然法的估计效果比最小二乘法好的结论[11]。如今常用的最大似然法有两种：平均风速μ和风速标准差σ估计法、平均风速μ和最大风速vmax估计法,用平均风速μ和最大风速vmax的多年平均值进行参数估计更具代表性,对于一年风速数据一般使用平均风速μ和风速标准差σ估计法。

平均风速μ和风速标准差σ的表达式如式(3)、(4)所示

(3)

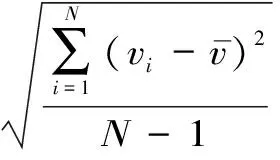
(4)

式中,N为总样本点的个数；vi为第i个时段风速的观测值。

参数k和A的估算分别见式(5)和式(6)

(5)

(6)

2 最大熵原理

最大熵原理的实质是在已知部分知识的前提下,关于未知分布最合理的推断就是符合已知知识的最随机的推断。

设风速序列v,概率密度函数为f(v),则其信息熵[15]为

(7)

式中,a为v的最小值；b为v的最大值；-lnf(v)为v的自信息。

在求得信息熵的最大值的同时,信号v应满足一定的约束

(8)

(9)

式(8)为归一化条件,即概率密度函数的积分为1；n可以取任意自然数,当n=1时,式(9)为数学期望的表达式。

为求得信息熵的最大值,利用拉格朗日乘数法构造函数

(10)

式中,λ0,λ1,…,λm为拉格朗日乘子,为n的最大值。

令L(v)对f(v)的偏导数等于0,得到f(v)的表达式

(11)

当最高阶次m取值不同时,概率密度函数表现出不同的性质,拟合效果也不同。m=0时, 风速的概率密度值为常数；m=1时,概率密度函数为单调增(或单调减)函数,这两种情况明显与事实不符。前人将m取2、3、4、5分别应用于陆上不同地区的风速分布拟合,据其经验,m取3、4的拟合效果明显比m=2要好,m=5的拟合效果与m取3、4相当,但计算复杂[8,11]。故本次取m为3、4进行研究,并比较其效果。m=3时成为四参数最大熵原理,m=4时成为五参数最大熵原理。

3 测风塔年风频分布

3.1 测风资料概况

某风电场两个测风塔2005年全年10 min时间间隔的测风资料,两个测风塔分别为1号和3号,测风塔资料包括10、25、40、50、60、70 m6个高度的数据,其中1号风塔70 m高度处风速12月份缺测,为避免风速大小的季节性对风速分布的影响,对于1号测风塔,只采用10、25、40、50、60m 5个高度资料进行本次研究。

参照GB/T 18710—2002《风电场风能资源评估方法》, 对11组风速资料进行整理,剔除不合理数据后,剔除风速值个数、最大风速及风速各次方均值见表1,数据完整度均高于90%。

3.2 参数拟合

根据式(3)～(6),求各测站威布尔分布参数。分别取最大熵分布函数f(v)的最高阶次为3次(4参数最大熵MEP4)和4次(5参数最大熵MEP5),采用空间信赖域优化算法[5]进行参数拟合,最大违反约束值取为10-6,并计算出最大熵值。

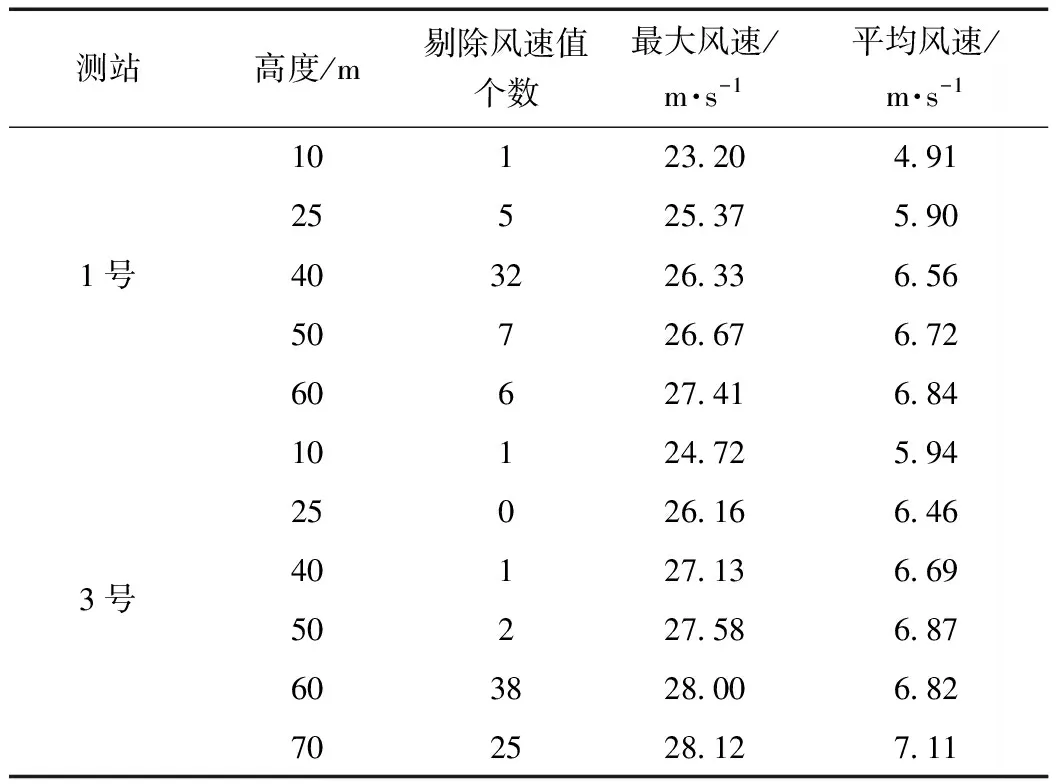
表1 测风资料完整度及风速

图1 3号测风塔各高度风速分布示意

篇幅限制,本文只列出3号测风塔的拟合效果图。3号测风塔6个高度的最大熵分布、威布尔分布曲线及实测频率直方图如图1所示。

3.3 拟合效果分析

图1的拟合效果表明,最大熵原理的拟合效果比威布尔分布好,主要表现在以下两个方面：威布尔分布形状扁平,频率峰值低于实测最大频率,最大熵分布的频率峰值与实测频率最大值非常接近；威布尔分布在零风速时概率密度为零,与实际情况不符。为具体分析,在表2中列出各测站最大频率和零到一风速段的频率值,并计算3种拟合方法的绝对误差,误差计算采用公式(12),经计算,除1号10 m和3号60 m外,最大熵分布的最大频率误差均低于威布尔分布,而其零到一风速段频率误差则在任何高度处都低于威布尔分布。

(12)

式中,P为实测频率；Pc为拟合频率。

在10、25 m高度处,四参数最大熵与五参数最大熵风频分布曲线在最大频率风速的估计上差距较大,40 m及其以上高度处,二者风频分布曲线基本重合；且随着高度的增加,风速的最大熵值有增大的趋势。上述两点表明,随高度增加最大熵原理更加适用于拟合风频分布。风速受地面障碍物和粗糙度的影响在高处减弱,使得高处风速信号更加符合最大熵原理所揭示的信息系统内部规律：系统在不加约束的条件下,总是向着最混乱的方向发展。

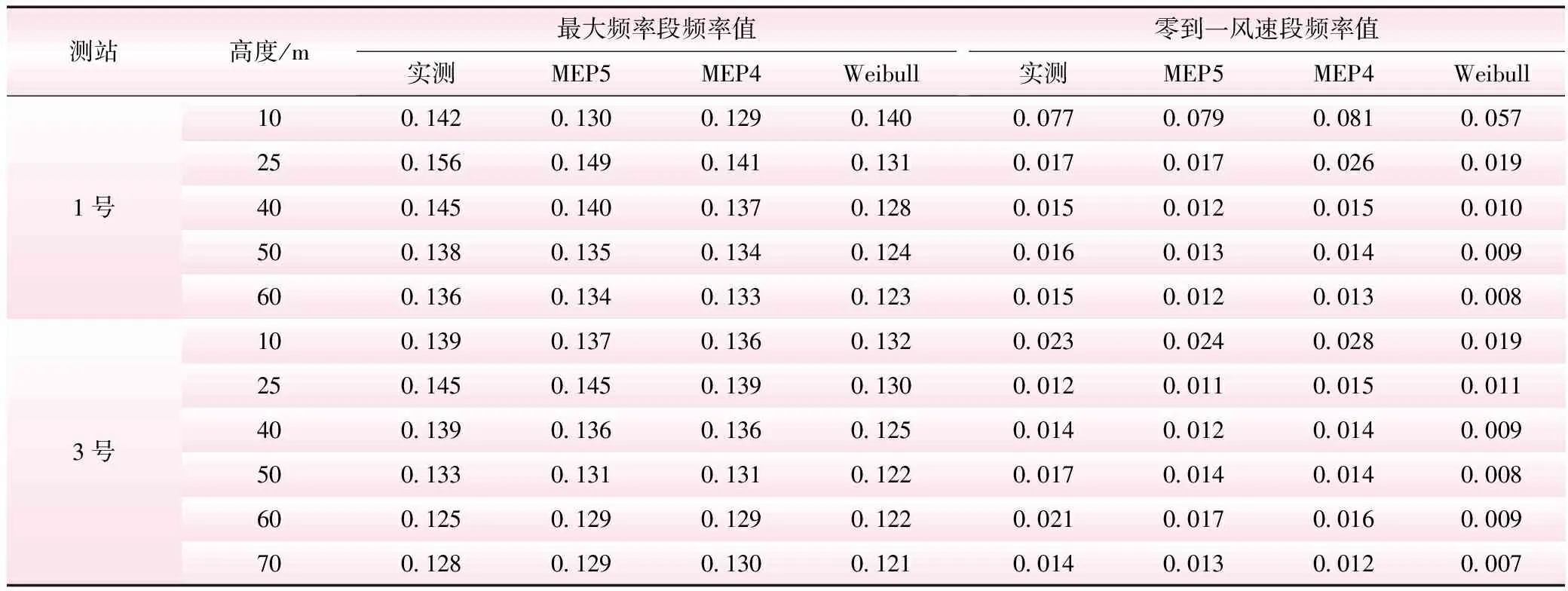
表2 最大频率段和零到一风速段频率值

表3 实测和风频分布模型计算平均有效风功率密度及误差

对威布尔分布和最大熵分布的总体频率误差进行分析,将风速分为N段,误差按公式(13)计算

(13)

式中,yi和yic为实测风速和拟合分布风速落在第i段内的概率。本次研究中,将风速按整数分段,第一段为0～1 m/s,第二段为1～2 m/s,依此类推。

在各高度处,五参数最大熵分布的误差均小于威布尔分布的误差；除3号测风塔10 m高度外,四参数最大熵分布的误差也小于威布尔分布的误差。对1号测风塔而言,随着高度的增加最大熵分布与威布尔分布误差差值增大,3号测风塔10、25 m和40 m高度处,误差差值呈增大趋势,40～60 m之间误差差值减小,后又趋于稳定。

3.4 平均有效风功率密度

根据实测风速、四参数最大熵、五参数最大熵和威布尔分布的概率密度函数,计算平均有效风功率密度,并采用绝对误差(见式(12))分析计算结果。实测和五参数最大熵、威布尔分布计算的误差见表3。

5参数最大熵原理计算的平均有效风能密度与实测非常接近,平均误差为1.71W/m2,而威布尔分布的计算误差为7.48 W/m2。

4 结 论

针对两个测风塔,分别应用威布尔分布和最大熵分布,进行了年风频分布的研究,得出如下结论：

(1)在拟合该测风塔年风频分布问题上,最大熵分布较威布尔分布有明显优势。最大熵分布的概率最大值和零到一风速段的拟合效果比威布尔分布好；最大熵分布的总体频率误差低于威布尔分布。

(2)随着高度的增加,风速分布更加符合最大熵原理。这表现在以下两个方面：四参数最大熵分布与五参数最大熵分布之间的差异在高处减小；风速的最大熵值随高度的增加而增大。

(3)根据五参数最大熵原理计算的平均有效风功率密度与实测非常接近,平均误差为1.71 W/m2,而威布尔分布的计算误差为7.48 W/m2。

(4)最大熵原理方法对于风频分布的普遍性适用性分析还有待进行。

[1]WENTINK T Jr. Study of Alaskan wind power and its possible applications, Final Report[R]. Alaska Univ., College. Geophysical Inst., 1976．[2]JUSTUS C, HARGRAVES W, YALCIN A. Nationwide assessment of potential output from wind-powered generators[J]. Journal of Applied Meteorology, 1976(15): 673- 678．

[3]胡文忠, 风速频率分布混合模型的研究[J]. 太阳能学报, 1994, 15(4): 353- 357．

[4]DEAVES D, LINES I. On the fitting of low mean windspeed data to the Weibull distribution[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 66(3): 169- 178．

[5]LI M S, LI X G. MEP-type distribution function: a better alternative to Weibull function for wind speed distributions[J]. Renewable Energy, 2005, 30(8): 1221- 1240．

[6]LI M, LI X. Investigation of wind characteristics and assessment of wind energy potential for Waterloo region, Canada[J]. Energy Conversion and Management, 2005, 46(18): 3014- 3033．

[8]CHELLALI F, KHELLAF A, BELOUCHRANI A, et al. A comparison between wind speed distributions derived from the max entropy principle and Weibull distribution. Case of study; six regions of Algeria[J]. Renewable & Sustainable Energy Reviews, 2012, 16(1): 379- 385．

[9]CARTA J A, RAMIREZ P. Analysis of two-component mixture Weibull statistics for estimation of wind speed distributions[J]. Renewable Energy, 2007, 32(3): 518- 531．

[10]ULGEN K, HEPBASLI A. Determination of Weibull parameters for wind energy analysis of Izmir, Turkey[J]. International Journal of Energy Research, 2002, 26(6): 495- 506．

[11]SEGURO J, LAMBERT T. Modern estimation of the parameters of the Weibull wind speed distribution for wind energy analysis[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2000, 85(1): 75- 84．

(责任编辑高 瑜)

StudyonAnnualWindFrequencyDistributionBasedonMaximumEntropyPrinciple

YU Yongjing, HE Yi, LIU Zhiyuan, XIONG Wanneng
(PowerChina Chengdu Engineering Corporation Limited, Chengdu 610072, Sichuan, China)

In order to study wind speed distribution characteristics and its variation with height in a wind field, the Weibull distribution and Maximum Entropy principle are applied to the fitting of annual wind speed frequency distribution of two wind towers. The results show that: (a) at the same height, the frequency peak value of Weibull distribution is lower than measured maximum frequency and the frequency peak value of Maximum Entropy principle is very close to measured value; and (b) at different heights, the Maximum Entropy principle shows a more obvious advantage with the increase of height. Furthermore, the mean errors of average effective wind power density calculated from five-parameter Maximum Entropy distribution and from Weibull distribution are 1.71 W/m2and 7.48 W/m2respectively．

annual wind frequency distribution; Maximum Entropy principle; Weibull distribution

2017- 04- 07

四川省科技支撑计划项目资助(2015GZ0138)

郁永静(1987—),女,河北邢台人,工程师,硕士,主要从事风能资源评估方面的研究工作．

TM614

：A

：0559- 9342(2017)06- 0093- 04