生态价值视角下土地最优利用研究*——以郑州市为实证

宋 剑， 席增雷

(1.中共唐山市委党校，河北唐山 063000； 2.天津大学环境科学与工程博士后流动站，天津 300072；3.河北大学经济学院,保定 071002)

生态价值视角下土地最优利用研究*
——以郑州市为实证

宋 剑1， 席增雷2， 3※

(1.中共唐山市委党校，河北唐山 063000； 2.天津大学环境科学与工程博士后流动站，天津 300072；3.河北大学经济学院,保定 071002)

[目的]试图探索能够直接应用于土地规划的方法思路与分析工具，为土地管理者和决策者提供分析和优化土地资源的参考。[方法]以郑州市为研究对象，采用计量公式计算、引用参考文献法得到土壤功能价值数据矩阵，将完整土壤功能价值指标数据导入因子分析模型，计算因子载荷矩阵，观察特征值及贡献率表，利用回归法计算样本综合得分。[结果]样本的各项土壤功能价值主要由4个主因子共同来决定，第一主因子为环境介质因子； 第二主因子为生态支持因子； 第三主因子为营养循环因子； 第四主因子为基础承载因子。[结论]综合得分排名靠前的大部分样本区域在4个主因子得分上均表现出较高的分数，实际规划中可以综合考虑使用目的、土质、地理区位、周边环境等因素权衡发展； 土壤的众多功能价值均比较高，但在第二主因子生态支持功能组上的优势最为明显的可规划为生态保护区； 在环境介质功能组上最有优势的，可优先发展农业和植被覆盖； 综合得分最低的区域大部分功能价值均较弱，规划中可适当考虑为建设承载区。

生态价值 土地利用 因子分析

0 引言

建设美丽中国，首先需要美丽的土壤，正确认知土壤的价值，亦是落实《土壤污染防治行动计划》、构建土壤环境治理体系的前提和基础。土壤作为一种未被全面认识的自然资本，是人类社会一切活动的物质基础[1]。然而随着城市化和工业化的不断发展，人类活动对土壤资源功能演化产生了深刻和持久的影响，包括土壤建设承载功能和土壤生产功能之间的此消彼长，土壤封闭导致的生态调节功能弱化等等。土壤功能的转化、弱化甚至特定功能的消失，造成很多地区土壤功能时间和空间上的平衡发生偏移，这些因素成为土壤利用价值最大化的桎梏，要实现土壤资源的最优化利用必须要对其进行科学规划[3]。

土壤功能演变为土地规划带来了很大的难度，要实现科学规划必须要解决2个关键问题。首先要改变土壤自然资本及其价值尚未得到全面发现、认识和计量的局面。除了容易为人们感知且易于量化的生产、基础承载等直接功能，生态环境调节、防洪减灾、保持生物多样性以及文化景观等难以量化的众多功能还很难直观的为公众所认知[5]，因此要逐步引导对土壤间接功能价值重要性的认识，进而逐步实现土壤各项功能的科学量化。土壤功能货币化分析能够比较土壤功能转化后的机会成本，衡量对人类福利产生的利弊。其次，土壤功能货币化计量理论与成果的转化是最优利用的关键。要选取科学的计量分析模型，从具体数据出发确定研究区域土壤优势功能或功能组，改变仅依据土地生产力和区位来确定最优用途和价值的简单思路[6]。

遵循如何将土壤各项功能因素融入到土地规划中去这一主线，文章力求探索能够直接应用于土地规划的方法思路与分析工具，为土地管理者和决策者提供分析和优化土地资源的参考，为土地资源利用、保护和土壤自然资本价值传播提供新视角。

1 因子分析模型的适用性分析

该文引入因子分析模型，将具有错综复杂关系的15项功能指标降维到少数综合因子，并根据样本得分与排名情况，提出确定研究区域最优土壤功能分配方案的新思路，通过对比土壤功能与土地利用类型的对应关系，比较土壤的各功能价值，选择最优开发用途或功能组合，从土壤合理利用的角度对土地利用规划提供建议。

如何透过目标区域的具体特性分辨出最适宜发展和最需要保护的功能或功能组[4]，往往是实际规划中的难题，因子分析模型恰恰能提供很好的思路，具有对接分析的实用性。因子分析模型可以简化计算过程，解决了多指标筛选和功能定位的难题，使分析方法和结论更具有推广性，还可以将错综复杂且相关性高的指标根据数据的客观表征分为一个功能组，便于快速准确地得出结论。

2 实证分析

2.1 数据来源

综合考虑郑州市土种类型、土壤数据库、农业数据库和土地利用数据库，并考虑了地形地貌等特征，在区域内选取56个样本点并提取相应土壤功能参数，采用计量公式计算、引用参考文献法，得到土壤功能价值数据矩阵，分析指标见表1。

表1 土壤功能指标体系

货币化指标代码货币化指标代码货币化指标代码气体调节功能价值X1消除二氧化硫价值X6生产功能价值X11气候调节价值X2消除氮氧化物价值X7原材料提供价值X12水分保持缓冲价值X3固尘价值X8建设承载功能价值X13碳存储价值X4防洪价值X9自然文化价值X14有机质蕴含价值X5废物处理价值X10生物多样性价值X15

2.2 因子模型分析

通过计算因子载荷矩阵，提取特征值大于1且累计贡献率达到86.06%的4个公因子作为综合变量。经过降维在以客观数据为支撑的前提下将原有15项评价指标划分为4类具有代表性的功能组，并且信息量损失较小。

将多指标体系降维后，就可以将公因子带入模型，以每个主因子方差贡献率的比重作为权数进行加权计算，利用回归法估计出各因子得分(Fi)，公式为：

F=∑Ai×Fi

(1)

Ai表示第i个公共因子的方差贡献率占总方差贡献率的比重[2]。通过样本因子得分的深入分析可以进一步拓宽规划思路。

2.3 样本数据价值矩阵的构成

依选取采集的郑州市56个采样点作为样本集，根据观测指标建立数据矩阵，为了消除数据间量纲及数量级不同所造成的影响，首先要对其进行标准化处理，最终使各变量的均值为0，标准差为1。标准化后对应各货币化指标数据见表2、表3。

表2 观测指标数据矩阵

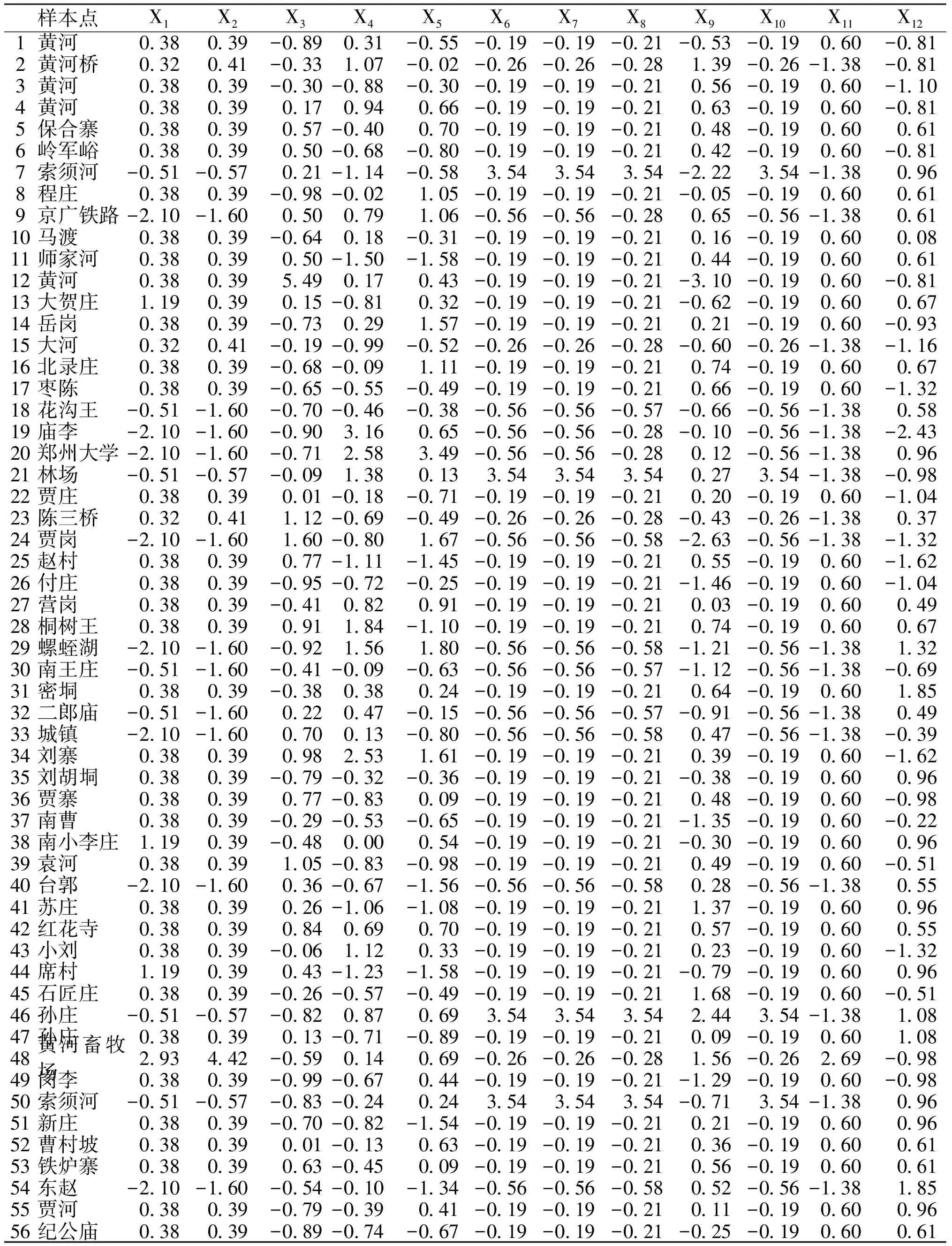
样本点X1X2X3X4X5X6X7X8X9X10X11X121黄河0 380 39-0 890 31-0 55-0 19-0 19-0 21-0 53-0 190 60-0 812黄河桥0 320 41-0 331 07-0 02-0 26-0 26-0 281 39-0 26-1 38-0 813黄河0 380 39-0 30-0 88-0 30-0 19-0 19-0 210 56-0 190 60-1 104黄河0 380 390 170 940 66-0 19-0 19-0 210 63-0 190 60-0 815保合寨0 380 390 57-0 400 70-0 19-0 19-0 210 48-0 190 600 616岭军峪0 380 390 50-0 68-0 80-0 19-0 19-0 210 42-0 190 60-0 817索须河-0 51-0 570 21-1 14-0 583 543 543 54-2 223 54-1 380 968程庄0 380 39-0 98-0 021 05-0 19-0 19-0 21-0 05-0 190 600 619京广铁路-2 10-1 600 500 791 06-0 56-0 56-0 280 65-0 56-1 380 6110马渡0 380 39-0 640 18-0 31-0 19-0 19-0 210 16-0 190 600 0811师家河0 380 390 50-1 50-1 58-0 19-0 19-0 210 44-0 190 600 6112黄河0 380 395 490 170 43-0 19-0 19-0 21-3 10-0 190 60-0 8113大贺庄1 190 390 15-0 810 32-0 19-0 19-0 21-0 62-0 190 600 6714岳岗0 380 39-0 730 291 57-0 19-0 19-0 210 21-0 190 60-0 9315大河0 320 41-0 19-0 99-0 52-0 26-0 26-0 28-0 60-0 26-1 38-1 1616北录庄0 380 39-0 68-0 091 11-0 19-0 19-0 210 74-0 190 600 6717枣陈0 380 39-0 65-0 55-0 49-0 19-0 19-0 210 66-0 190 60-1 3218花沟王-0 51-1 60-0 70-0 46-0 38-0 56-0 56-0 57-0 66-0 56-1 380 5819庙李-2 10-1 60-0 903 160 65-0 56-0 56-0 28-0 10-0 56-1 38-2 4320郑州大学-2 10-1 60-0 712 583 49-0 56-0 56-0 280 12-0 56-1 380 9621林场-0 51-0 57-0 091 380 133 543 543 540 273 54-1 38-0 9822贾庄0 380 390 01-0 18-0 71-0 19-0 19-0 210 20-0 190 60-1 0423陈三桥0 320 411 12-0 69-0 49-0 26-0 26-0 28-0 43-0 26-1 380 3724贾岗-2 10-1 601 60-0 801 67-0 56-0 56-0 58-2 63-0 56-1 38-1 3225赵村0 380 390 77-1 11-1 45-0 19-0 19-0 210 55-0 190 60-1 6226付庄0 380 39-0 95-0 72-0 25-0 19-0 19-0 21-1 46-0 190 60-1 0427营岗0 380 39-0 410 820 91-0 19-0 19-0 210 03-0 190 600 4928桐树王0 380 390 911 84-1 10-0 19-0 19-0 210 74-0 190 600 6729螺蛭湖-2 10-1 60-0 921 561 80-0 56-0 56-0 58-1 21-0 56-1 381 3230南王庄-0 51-1 60-0 41-0 09-0 63-0 56-0 56-0 57-1 12-0 56-1 38-0 6931密垌0 380 39-0 380 380 24-0 19-0 19-0 210 64-0 190 601 8532二郎庙-0 51-1 600 220 47-0 15-0 56-0 56-0 57-0 91-0 56-1 380 4933城镇-2 10-1 600 700 13-0 80-0 56-0 56-0 580 47-0 56-1 38-0 3934刘寨0 380 390 982 531 61-0 19-0 19-0 210 39-0 190 60-1 6235刘胡垌0 380 39-0 79-0 32-0 36-0 19-0 19-0 21-0 38-0 190 600 9636贾寨0 380 390 77-0 830 09-0 19-0 19-0 210 48-0 190 60-0 9837南曹0 380 39-0 29-0 53-0 65-0 19-0 19-0 21-1 35-0 190 60-0 2238南小李庄1 190 39-0 480 000 54-0 19-0 19-0 21-0 30-0 190 600 9639袁河0 380 391 05-0 83-0 98-0 19-0 19-0 210 49-0 190 60-0 5140台郭-2 10-1 600 36-0 67-1 56-0 56-0 56-0 580 28-0 56-1 380 5541苏庄0 380 390 26-1 06-1 08-0 19-0 19-0 211 37-0 190 600 9642红花寺0 380 390 840 690 70-0 19-0 19-0 210 57-0 190 600 5543小刘0 380 39-0 061 120 33-0 19-0 19-0 210 23-0 190 60-1 3244席村1 190 390 43-1 23-1 58-0 19-0 19-0 21-0 79-0 190 600 9645石匠庄0 380 39-0 26-0 57-0 49-0 19-0 19-0 211 68-0 190 60-0 5146孙庄-0 51-0 57-0 820 870 693 543 543 542 443 54-1 381 0847孙庄0 380 390 13-0 71-0 89-0 19-0 19-0 210 09-0 190 601 0848黄河畜牧场2 934 42-0 590 140 69-0 26-0 26-0 281 56-0 262 69-0 9849岗李0 380 39-0 99-0 670 44-0 19-0 19-0 21-1 29-0 190 60-0 9850索须河-0 51-0 57-0 83-0 240 243 543 543 54-0 713 54-1 380 9651新庄0 380 39-0 70-0 82-1 54-0 19-0 19-0 210 21-0 190 600 9652曹村坡0 380 390 01-0 130 63-0 19-0 19-0 210 36-0 190 600 6153铁炉寨0 380 390 63-0 450 09-0 19-0 19-0 210 56-0 190 600 6154东赵-2 10-1 60-0 54-0 10-1 34-0 56-0 56-0 580 52-0 56-1 381 8555贾河0 380 39-0 79-0 390 41-0 19-0 19-0 210 11-0 190 600 9656纪公庙0 380 39-0 89-0 74-0 67-0 19-0 19-0 21-0 25-0 190 600 61

3 利用因子分析方法计算样本综合得分

3.1 计算相关系数矩阵

实证分析主要采用SPSS18.0统计分析软件进行。获得原始样本数据矩阵后，通过整理计算将其输入计算机，根据因子分析的步骤进行分析。首先对这些指标进行预处理，求出所有指标的相关系数矩阵表。

3.2 计算因子载荷矩阵

接下来计算因子载荷矩阵，观察特征值及贡献率表(表4)，可以看出前4个因子的累计贡献率达到82.846%，并且特征值大于1，表明这4个公因子方差占全部因子方差的82.846%，所包含的信息量已达到原来总信息量的绝大部分，鉴于此，提取4个公因子作为综合变量。这样一来，原来的12项货币化指标转化为4项综合指标，达到了降维分析目的。

表3 相关系数矩阵

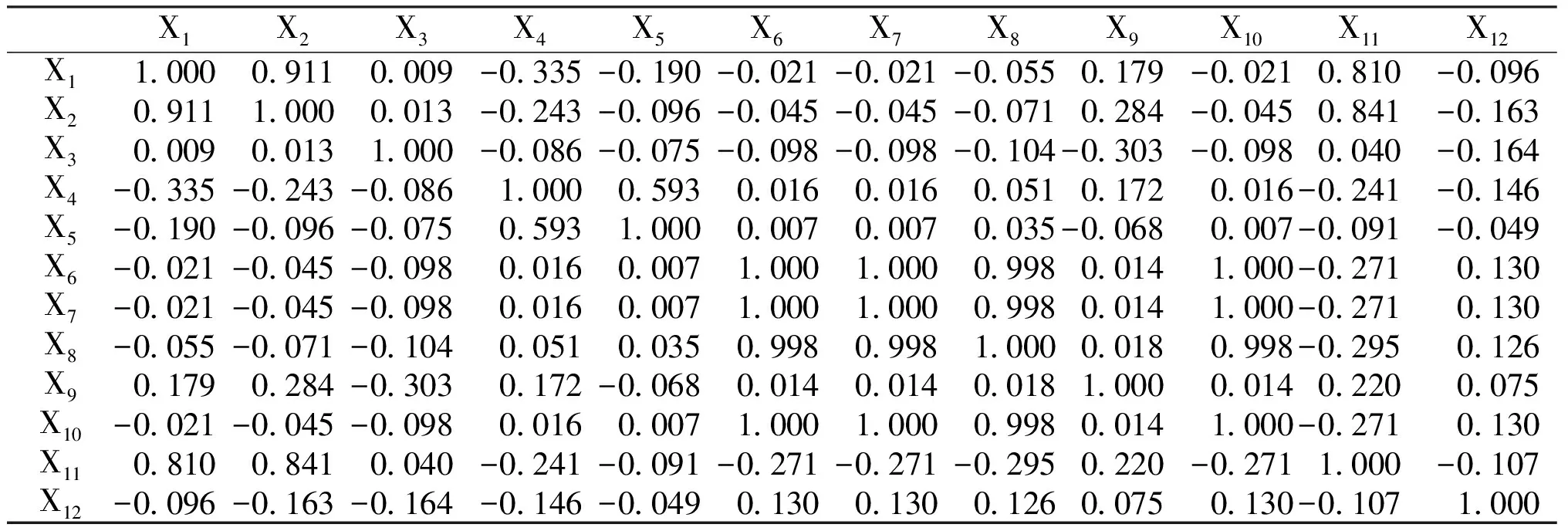
X1X2X3X4X5X6X7X8X9X10X11X12X11 0000 9110 009-0 335-0 190-0 021-0 021-0 0550 179-0 0210 810-0 096X20 9111 0000 013-0 243-0 096-0 045-0 045-0 0710 284-0 0450 841-0 163X30 0090 0131 000-0 086-0 075-0 098-0 098-0 104-0 303-0 0980 040-0 164X4-0 335-0 243-0 0861 0000 5930 0160 0160 0510 1720 016-0 241-0 146X5-0 190-0 096-0 0750 5931 0000 0070 0070 035-0 0680 007-0 091-0 049X6-0 021-0 045-0 0980 0160 0071 0001 0000 9980 0141 000-0 2710 130X7-0 021-0 045-0 0980 0160 0071 0001 0000 9980 0141 000-0 2710 130X8-0 055-0 071-0 1040 0510 0350 9980 9981 0000 0180 998-0 2950 126X90 1790 284-0 3030 172-0 0680 0140 0140 0181 0000 0140 2200 075X10-0 021-0 045-0 0980 0160 0071 0001 0000 9980 0141 000-0 2710 130X110 8100 8410 040-0 241-0 091-0 271-0 271-0 2950 220-0 2711 000-0 107X12-0 096-0 163-0 164-0 146-0 0490 1300 1300 1260 0750 130-0 1071 000

表4 特征值及贡献率

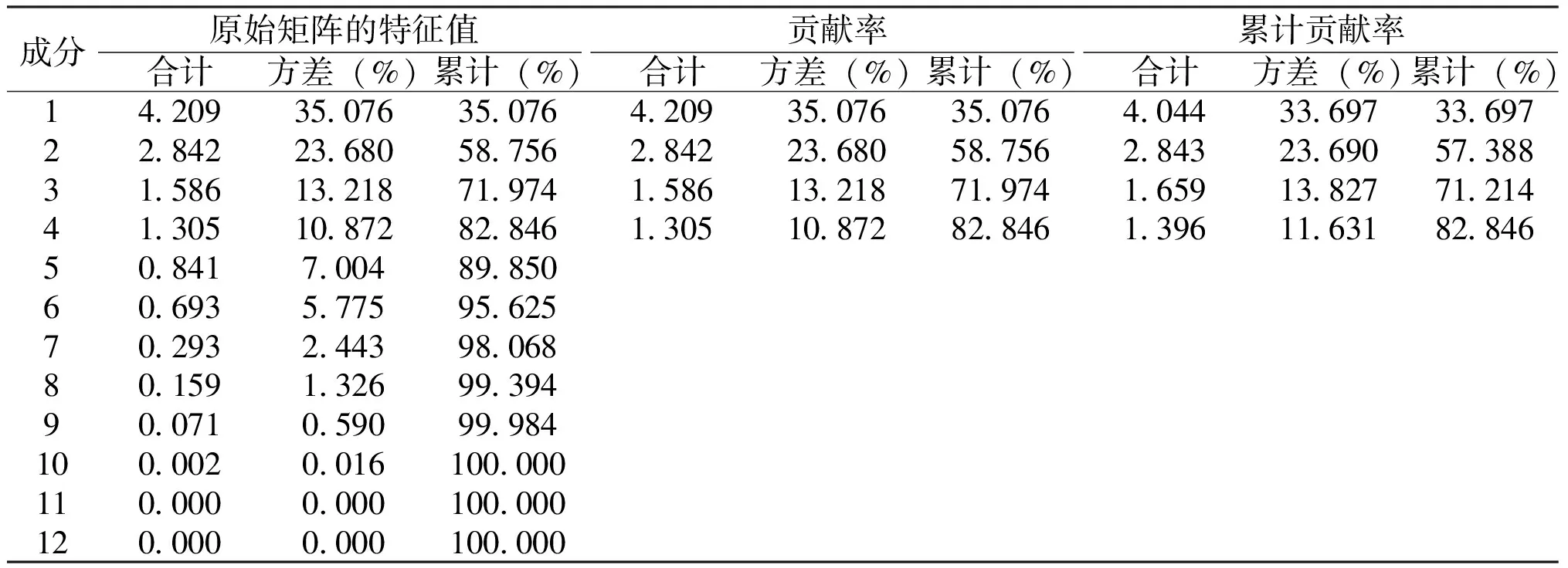
成分原始矩阵的特征值贡献率累计贡献率合计方差(%)累计(%)合计方差(%)累计(%)合计方差(%)累计(%)14 20935 07635 0764 20935 07635 0764 04433 69733 69722 84223 68058 7562 84223 68058 7562 84323 69057 38831 58613 21871 9741 58613 21871 9741 65913 82771 21441 30510 87282 8461 30510 87282 8461 39611 63182 84650 8417 00489 85060 6935 77595 62570 2932 44398 06880 1591 32699 39490 0710 59099 984100 0020 016100 000110 0000 000100 000120 0000 000100 000

从共同度信息表可以看出，公因子对每一个原始变量的解释能力都较强。通过因子载荷矩阵，可得写出各变量的因子模型，但是由于4个因子在原变量上的载荷值相差不大，不容易对公因子进行归类和解释，因此还需要对公因子进行方差最大化旋转(表5)，因子旋转后累计方差比没有改变，不会影响到原有变量的共同度，但却重新分配了各个因子解释原有变量的方差，使得因子更容易解释。

旋转后的因子载荷矩阵发生了很大变化，各因子在每项指标上的差异也显现出来，解释起来也相对容易。根据因子载荷绝对值的大小，将在某一因子上载荷绝对值比较大的几个指标分为一组。

表5 旋转因子载荷矩阵a

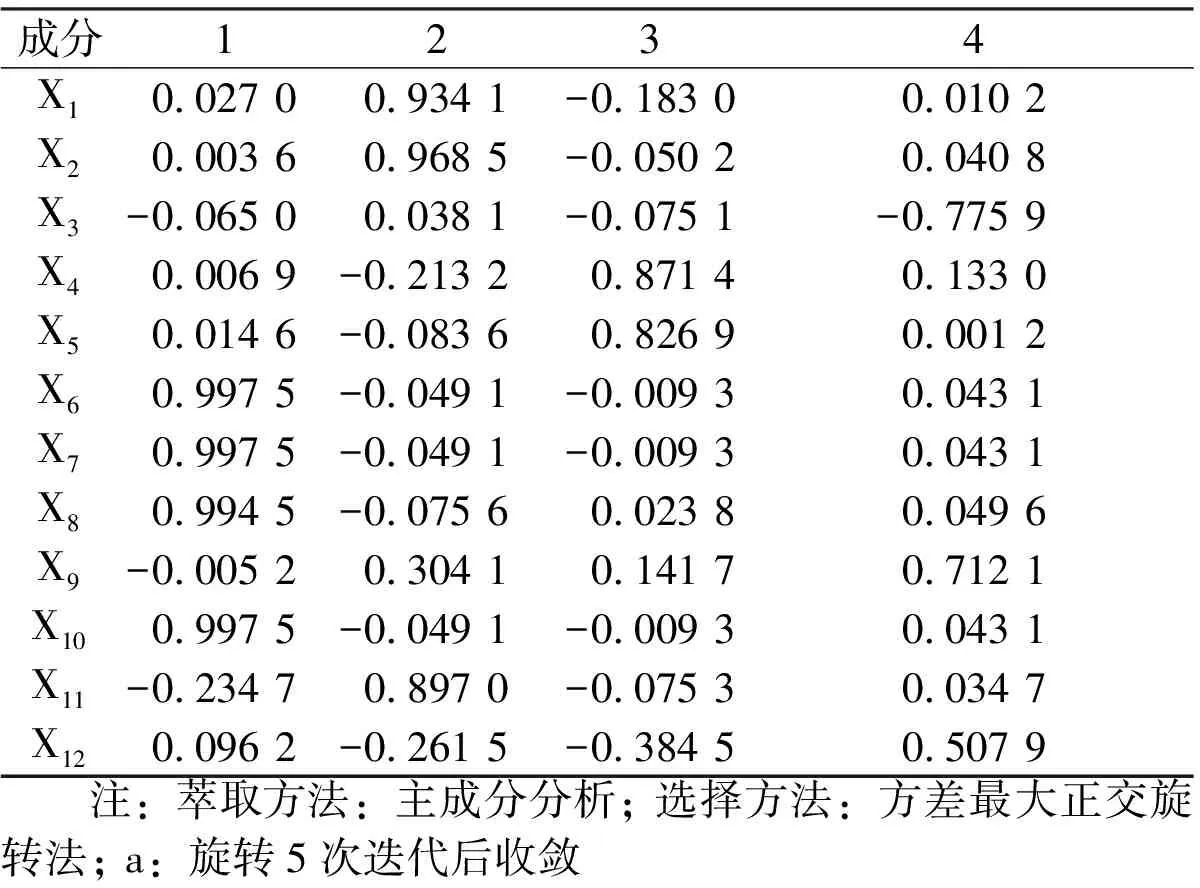
成分1234X10 02700 9341-0 18300 0102X20 00360 9685-0 05020 0408X3-0 06500 0381-0 0751-0 7759X40 0069-0 21320 87140 1330X50 0146-0 08360 82690 0012X60 9975-0 0491-0 00930 0431X70 9975-0 0491-0 00930 0431X80 9945-0 07560 02380 0496X9-0 00520 30410 14170 7121X100 9975-0 0491-0 00930 0431X11-0 23470 8970-0 07530 0347X120 0962-0 2615-0 38450 5079 注：萃取方法：主成分分析；选择方法：方差最大正交旋转法；a：旋转5次迭代后收敛

3.3 计算因子得分

将多指标体系降维后，就可以将公因子带入模型，利用回归法估计出各因子得分(Fi)，以每个主因子方差贡献率的比重作为权数进行加权计算，公式为：F=∑Ai×Fi，Ai表示第i个公共因子的方差贡献率占总方差贡献率的比重。各因子得分和综合货币化：

F=0.41×F1+0.29×F2+0.17×F3+0.14×F4

(2)

依据上述公式利用统计软件可以得到各样本综合得分F，见表6。综上，根据该文货币化模型，样本的各项土壤功能价值主要由以上4个主因子共同来决定，每一个主因子都从不同的侧面反映了土壤的部分功能价值。仅仅单独地分析某一个因子是不够的，而是要综合分析总的得分情况，以便对整个土壤功能做出正确可观的货币化分析。

表6 土壤功能价值综合得分

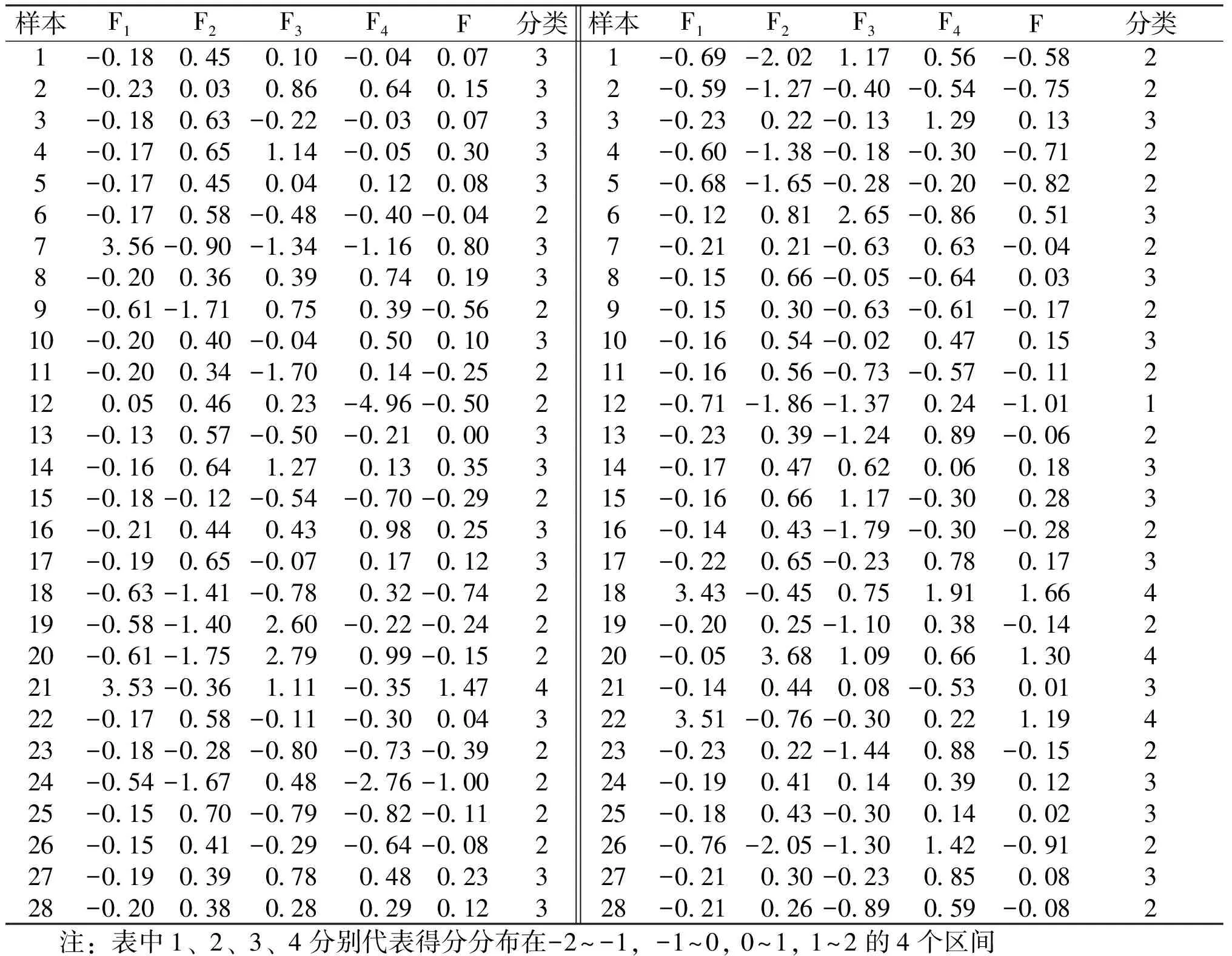
样本F1F2F3F4F分类样本F1F2F3F4F分类1-0 180 450 10-0 040 0731-0 69-2 021 170 56-0 5822-0 230 030 860 640 1532-0 59-1 27-0 40-0 54-0 7523-0 180 63-0 22-0 030 0733-0 230 22-0 131 290 1334-0 170 651 14-0 050 3034-0 60-1 38-0 18-0 30-0 7125-0 170 450 040 120 0835-0 68-1 65-0 28-0 20-0 8226-0 170 58-0 48-0 40-0 0426-0 120 812 65-0 860 51373 56-0 90-1 34-1 160 8037-0 210 21-0 630 63-0 0428-0 200 360 390 740 1938-0 150 66-0 05-0 640 0339-0 61-1 710 750 39-0 5629-0 150 30-0 63-0 61-0 17210-0 200 40-0 040 500 10310-0 160 54-0 020 470 15311-0 200 34-1 700 14-0 25211-0 160 56-0 73-0 57-0 112120 050 460 23-4 96-0 50212-0 71-1 86-1 370 24-1 01113-0 130 57-0 50-0 210 00313-0 230 39-1 240 89-0 06214-0 160 641 270 130 35314-0 170 470 620 060 18315-0 18-0 12-0 54-0 70-0 29215-0 160 661 17-0 300 28316-0 210 440 430 980 25316-0 140 43-1 79-0 30-0 28217-0 190 65-0 070 170 12317-0 220 65-0 230 780 17318-0 63-1 41-0 780 32-0 742183 43-0 450 751 911 66419-0 58-1 402 60-0 22-0 24219-0 200 25-1 100 38-0 14220-0 61-1 752 790 99-0 15220-0 053 681 090 661 304213 53-0 361 11-0 351 47421-0 140 440 08-0 530 01322-0 170 58-0 11-0 300 043223 51-0 76-0 300 221 19423-0 18-0 28-0 80-0 73-0 39223-0 230 22-1 440 88-0 15224-0 54-1 670 48-2 76-1 00224-0 190 410 140 390 12325-0 150 70-0 79-0 82-0 11225-0 180 43-0 300 140 02326-0 150 41-0 29-0 64-0 08226-0 76-2 05-1 301 42-0 91227-0 190 390 780 480 23327-0 210 30-0 230 850 08328-0 200 380 280 290 12328-0 210 26-0 890 59-0 082 注：表中1、2、3、4分别代表得分分布在-2～-1，-1～0，0～1，1～2的4个区间

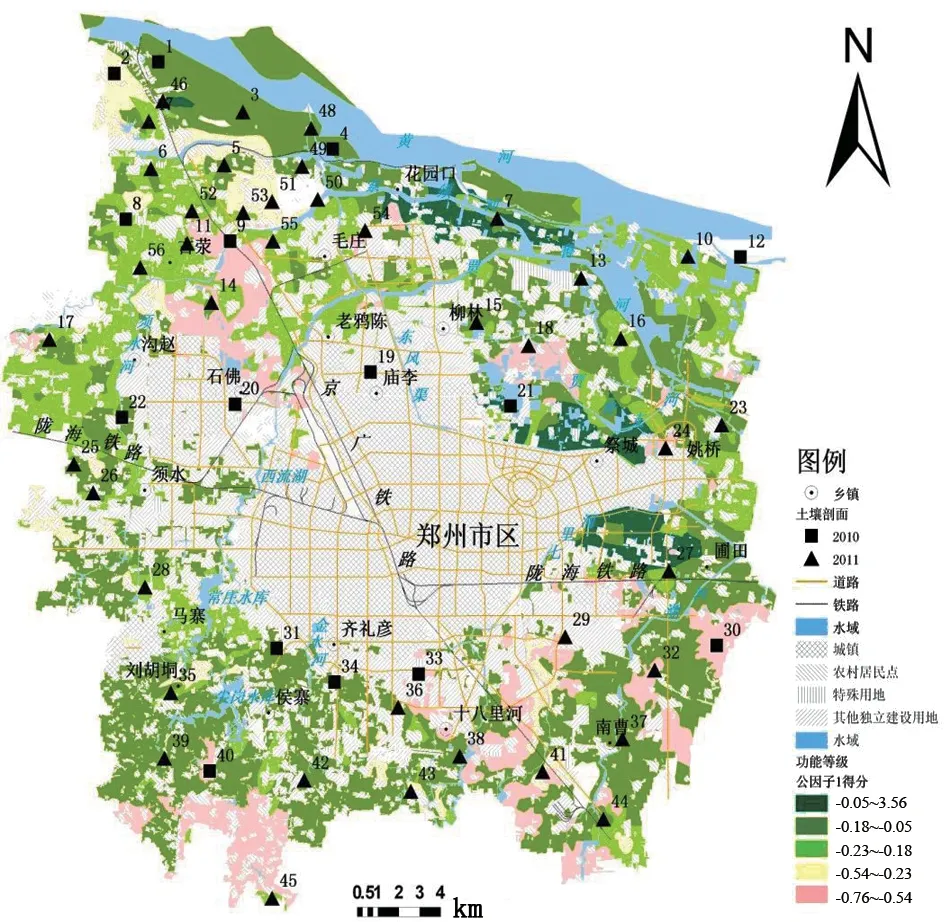
图1 第一主因子得分空间分布

4 结论与应用分析

因子分析结论提供了2个观察视角。横向考虑样本单位在各主因子上的得分情况，可以得到就某一区域而言土壤最适合发挥的功能。纵向上根据土壤功能的因子得分等级结果，可以直观得到某一类功能方面，哪些研究区域可以重点规划利用，而且便于比较不同利用条件下土壤资源对人类福利影响的差异，交叉分析再结合地理信息系统的空间应用，便能更好地服务于实际规划。

4.1 单因子得分分析

(1)第一主因子得分分析。第一个主因子代表的功能信息最多，在气体调节功能价值、气候调节价值、消除二氧化硫价值、消除氮氧化物价值、固尘价值、生产功能价值、废物处理价值指标的载荷比较大，代表了环境调节与生产力功能，可以命名为环境介质因子。

图2 第二主因子得分空间分布 图3 第三主因子得分空间分布

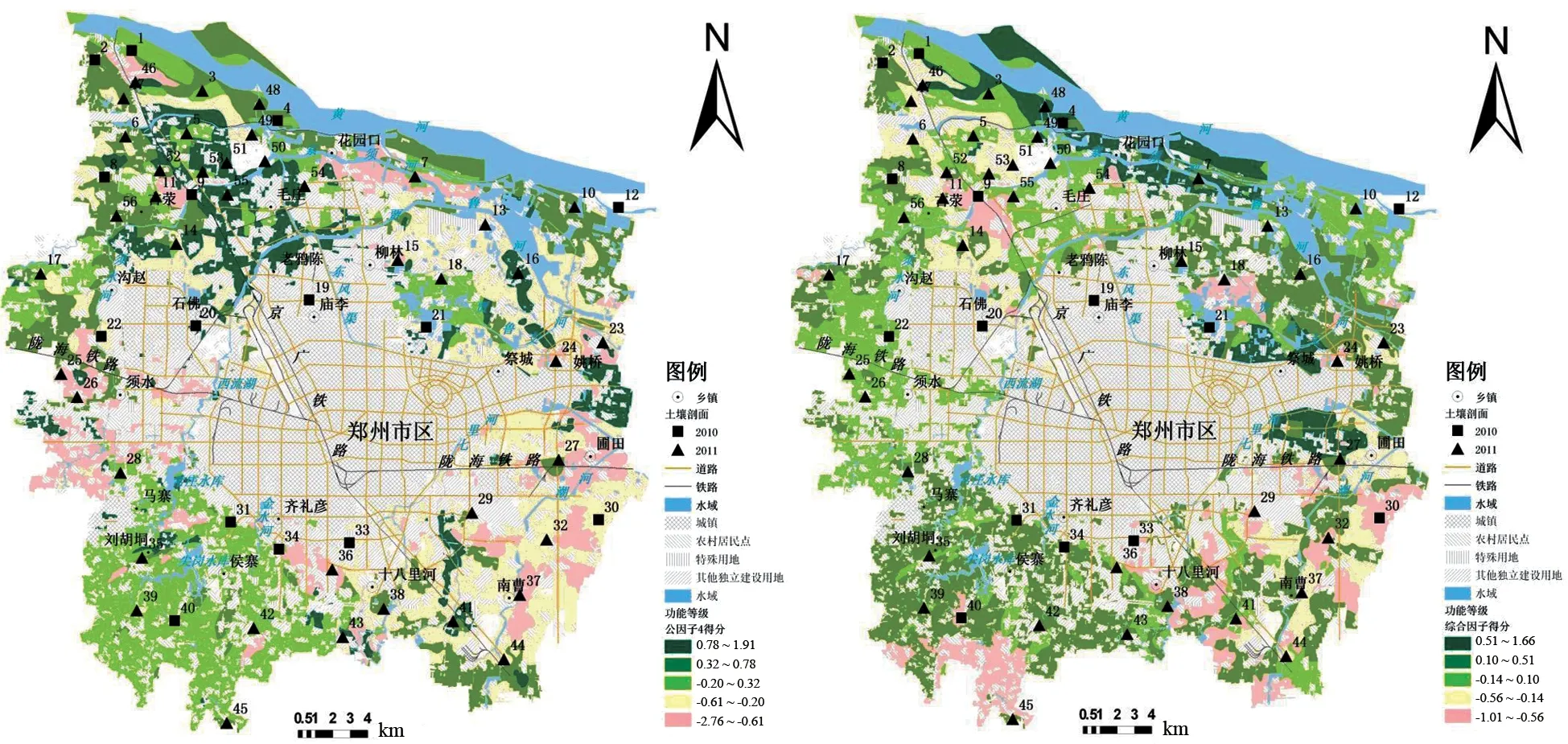
图4 第四主因子得分空间分布 图5 郑州市土壤功能价值综合得分分布

得分最高的样本为7号(京河村)，显示了此区域在环境介质功能价值很大，具有环境调节的优势，在规划中应侧重此类功能的保护和潜力挖掘，减少建设承载等其它功能的比重。观察分值为-0.76的第54号样本(东赵)，此区域得分最低，生态环境调节与生产功能弱，这与其土地应用类型主要为农村居民点相吻合，因此在规划中应一方面控制土壤封闭的扩大速度，另一方面开展土地整治，增加植被的面积与空间配比，逐步增加环境介质价值。

从第一主因子得分分布图1上可以清晰地看出不同地区在第一主因子上的得分情况，大部分地区功能价值等级较高，但是得分较低的地区仍然很多，且在各个地区均有分布。同时从图1也可以直观找到在第一主因子上具有突出优势的地区，如西南部和东北部，这些地区土壤的性质和状况决定了在发挥环境生态与生产力功能上的天然优势，可以因地制宜发挥这些土壤功能。

(2)第二主因子得分分析。第二公因子在原材料价值、自然文化价值和生物多样性价值的载荷比较大，同时包含了生产功能、气体调节和气候调节的部分信息，代表了生态支持能力，即生态支持因子。

从得分山看第48个样本点(黄河畜牧场)得分为3.68，明显高于其他区域，此区域在岗李村黄河滩，土种为砂壤土，表明这一区域在发挥防洪、原材料、自然文化价值和生物多样性等功能价值方面具有独特的自然优势，在规划中应大力发扬这一类功能优势，减少生产功能和建设等功能的规划，达到效用最大化。

从分布图2可以找到在生态支持类功能价值上具有优势的地区，分别是北部黄河沿岸和东部部分地区，这些区域植被种类丰富，林带密集，土质适宜作为基础原材料，具有很好的自然景观，能够实现人们对文化和休憩娱乐的需求，因此这些地带可以规划为动物保护区、公园、原材料基地等。

(3)第三主因子得分分析。第三公因子在碳存储和有机质蕴含价值上的因子载荷值最大，代表了土壤营养循环功能价值，即营养循环因子。

郑州市土壤主要为潮土和褐土亚类，土种丰富，观察分布图(图3)并没有出现极好或者极差的区域，由于在土种、利用类型等方面的差异，土壤中营养元素含量、容重、pH值、阳离子交换量等也有很大不同，实际规划中可根据对应得分高低进行斟酌。比如在西部岳岗和郑州大学采样点附近地区，土壤的营养循环价值就很突出，这些地区不仅可以大力发展农业种植或植被覆盖，而且还应该采取措施加以保护。

(4)第四主因子得分分析。4个公因子主要集中了建设居住功能价值和水资源缓冲过滤价值、防洪减灾功能价值的大部分信息，可以命名为基础承载因子。

从因子载荷矩阵中可以看出，建设承载功能价值与其他两项功能价值在第四主因子上的值绝对值很大但方向相反，这也更加确定了建设承载功能和其它功能之间的替代关系。以得分比较低的第24号样本为例，此样本点分布在贾岗区域，土种为盐化砂壤土，地类为城镇，地面封闭度高于其它耕地、草地等研究区域，地下水资源缓冲过滤功能价值低，在均衡了水资源缓冲和建设承载等主要功能价值后得分为负，也说明了相对于其他地区，水资源功能价值过于低，因此在规划中应减少占用，改善土质，提高水资源缓冲过滤能力。相反的在土质不适合缓冲过滤功能的区域可以适当发展为建设用地。

从分布图4上可以看出，东部及东南部的祭城乡花沟王村、惠济区东赵村等地为盐化砂壤土、城镇和道路，得分为负且绝对值最大，这些地区适宜发展基础设施建设，价值最高代价最小，相反地，图4绿色标注地带由于土壤饱和导水率、空气容重等指标适宜发挥其水质净化和防洪减灾功能，开发利用时要考虑这些功能的发挥和保护。

4.2 综合得分分析

综合因子分析平衡了地区各功能组的优势差异，可以对其进行排序。从主因子综合得分表可看出，得分最高的区域为岗李村黄河滩、刘寨乡、西双桥村、黄河滩地、北录庄。其中后3个样本点地类为耕地，这些区域土壤肥沃，植被茂盛，在生态调节、污染降解、灾害防护、生产、地下水缓冲过滤等方面均具有不错的表现，这从4个主因子得分上也得到了数据印证。

综合得分排名靠前的大部分样本区域在4个主因子得分上均表现出较高的分数，具有较高的各类功能价值，这也提升了此类地区规划的灵活度，实际规划中可以综合考虑使用目的、土质、地理区位、周边环境等因素权衡发展。

并非所有的综合得分比较高的区域所有主因子得分均高，反之亦然。例如第48号样本李村黄河滩区域，地类为林地，其主要在第二个主因子上表现突出，在其它主因子上并没有得到较高的分数，综合得分全部依靠在第二个主因子上得分的拉动，表明其最适宜发挥防洪、原材料、自然文化和生物多样性等功能价值。第40号样本为台郭区域，综合得分最低，地类为农村居民点，其在第一、第二、第三主因子上的得分均比较低，而在第四个主因子上的得分为正，表明这一区域并非所有土壤功能价值均较低，而是土壤的多功能演变为建设功能，功能单一化。

从分布图中可以看出，土壤货币化综合价值最高的区域集中在郑州市北部黄河沿岸，土壤的众多功能价值均比较高，但在第二主因子生态支持功能组上的优势最为明显，可以规划为生态保护区。

图中标注为浅绿色区域分布最为广泛，这些区域综合功能价值较大，具有很大规划灵活度，结合单因子分布图分析主要在环境介质功能组上最有优势，因此可以优先发展农业和植被覆盖，发挥环境功能。根据供给功能和环境服务功能的互补关系原理，可以同时获取经济效益和环境效益。

综合得分最低的区域主要集中在东南和东北的局部区域，结合单因子分析发现大部分功能价值均较弱，表明这些区域土质贫瘠，植物生长能力低，水源循环质量和数量均不高，规划中可以适当考虑为建设承载区，但同时应重视环境调节功能的提升，采取增加植被密度，逐步开展开方土壤的整治工作，实现各项功能的协调发展。

[1] Costanza R，Darge R，Groot R，et al.The Value of the World′s Ecosystem Services and Natural Capital.Nature， 1997, 38(7): 253～260

[2] 谢贤政. 环境资源经济价值评估.北京：中国环境科学出版社， 2011

[3] 谢高地， 鲁春霞，成升魁.全球生态系统服务价值评估研究进展.资源科学， 2001, 23(6): 5～9

[4] 谢高地， 鲁春霞，冷允法，等.青藏高原生态资产的价值评估.自然资源学报， 2003, 18(2): 189～196

[5] 王秀丽， 吴克宁，李玲，等.区域土壤主要功能评价研究——以郑州市为例.土壤通报， 2011, 42(4): 770～776

[6] 吴克宁， 王秀丽，关小克，等.区域生态服务功能价值的变化——以郑州市郊区为例.城市环境与城市生态， 2007, 20(4): 24～28

[7] 邵晓梅. 基于GIS与景观生态学的土壤资源格局分析——以鲁西北地区为例.中国农业资源与区划， 2004, 25(6): 11～16

[8] 席增雷. 土壤自然资本价值计量研究.北京：人民出版社， 2016

[9] 李玲， 段英华，徐明岗，等.河北省不同利用方式农田土壤氮磷环境风险分析.中国农业资源与区划， 2016, 37(7): 96～100

[10]杨飞， 王伟，廖顺宝，等.县级土壤环境功能区划研究与示范——以登封市为例.中国农业资源与区划， 2016, 37(2): 142～147

OPTIMAL LAND USE UNDER THE VIEW OF SOIL ECOLOGICAL VALUE*

Song Jian1，Xi Zenglei2,3※

(1. Party School of CPC Tangshan Municipal Party Committee,Tangshan, Hebei 063000, China; 2.Environmental Science and Engineering Post-doctoral Mobile Stations,Tianjin University,Tianjin 300072,China; 3.School of Economics,Hebei University,Baoding 071002,China)

objective of this paper is to explore a method which can be directly applied to land planning and analysis, and to provide a reference for land managers and policy makers. It established soil function value data matrix by the formula calculation and reference method, and then imported the soil function value index into the factor analysis model, calculated the characteristic value and contribution rate, and calculated the sample composite scores using the regression method. The results showed that soil function value was mainly composed of four main factors, i.e., the environment medium factor, ecological support factor, nutrient cycling factor, and basis load factor. The four main factors scored showed higher scores in the areas with higher comprehensive score. The balance development of the factors such assoil, geographical location, and surrounding environment should be considered in practical planning. The area with higher ecological function factor could be planned as ecological reserve region, while the area with higher environmental function could develop agriculture and improve vegetation cover. The lowest scores area could be appropriately considered as load bearing region.

ecological value; land use; factor analysis

10.7621/cjarrp.1005-9121.20170522

2016-02-19

宋剑(1979—)，男，河北唐山人，副教授。研究方向：农业经济。※通讯作者：席增雷(1976—)，男，河北邢台人，博士后、副教授。研究方向：自然资本评价、土地评价。Email： 641600251@qq.com

*资助项目：河北省高层次人才资助项目“河北省土壤自然资本价值研究”(A201500166)； 河北省软科学研究计划项目“京津冀科技创新激励政策比较研究”(16456223D)； 河北省生态与环境发展研究中心资助； 河北大学资源利用与环境保护研究中心资助

F301.2

A

1005-9121[2017]05147-08