某同源平衡及定位电液伺服系统模糊分数阶PID控制⋆

孙 浩，高 强，刘国栋，侯远龙，汤巧戈

（1.南京理工大学机械工程学院，南京 210094；2.北方自动控制技术研究所，太原 030006）

某同源平衡及定位电液伺服系统模糊分数阶PID控制⋆

孙 浩1，高 强1，刘国栋2，侯远龙1，汤巧戈1

（1.南京理工大学机械工程学院，南京 210094；2.北方自动控制技术研究所，太原 030006）

针对某同源平衡及定位电液伺服系统，设计了一种用于该系统的模糊分数阶PID控制器。使用模糊规则来调节分数阶PID的参数，提高了分数阶PID控制器的响应速度，增强了分数阶PID鲁棒性。模糊分数阶PID控制器能使系统很快进入稳定状态，比分数阶PID控制器表现出较好的控制性能。通过半实物仿真实验可知模糊分数阶PID控制器在响应速度、超调量及稳定误差等方面均优于分数阶PID控制器，且对外部负载扰动具有较好的鲁棒性。

同源平衡及定位，模糊分数阶PID控制器，电液伺服系统

0 引言

火炮身管的质心不在耳轴轴心所产生的非平衡质量诱发的系统非平衡扰动将严重恶化身管平衡定位控制性能［1-3］，现行的身管平衡方法主要是外部施加平衡力方法。外部施加平衡力方法包括平衡机平衡和配重平衡，该类方法采用机械弹簧、气动或液压助力方式，通过施加外部机械储能机构实现运动过程中系统非平衡力矩的补偿［4-8］，难以实现任意工况下的实时主动平衡要求。

针对大口径身管运动，韩崇伟［9］等提出了一种三腔液压缸与蓄能器混合平衡机结构，采用蓄能器与液压缸的平衡腔平衡部分负载，以降低液压缸所需的驱动力。本文提出的基于三腔动力液压缸的身管运动主动平衡及定位控制方法，其优点在于：采用三腔动力液压缸作为同一驱动源，其平衡腔实现系统非平衡力的主动平衡补偿，其驱动腔进行身管定位控制，通过构建反馈同步控制系统，实现身管运动的平稳精准控制。该方法本质上为被动配平过程，只能补偿部分非平衡力，从原理上系统运动过程将不可避免地存在非平衡扰动因素，这必然将限制身管最终定位性能及伺服系统稳定性。

本文采用模糊分数阶PIλDμ控制实现火炮身管运动的角度控制。模糊分数阶PIλDμ控制器逐渐在应用于实际控制系统，为模糊分数阶PIλDμ控制策略的研究提供了一种更可靠的解决方案［10］。模糊分数阶系统控制器较分数阶控制器有更强的鲁棒性，故其不仅在运动控制中具有更好的控制性能，而且可以准确描述动态系统的属性特征［11］。

1 系统工作原理和数学模型

1.1 系统组成及工作原理

同源平衡及定位电液伺服控制系统模型如图1所示动力液压缸有3个腔，分别是上、下腔及平衡腔，其中上腔和下腔可合称为驱动腔。

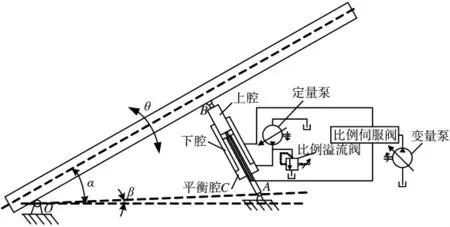
图1 同源平衡及定位电液伺服系统模型

定量泵通过比例减压阀与三腔动力液压缸的平衡腔相连，通过控制平衡腔的压力控制其输出的平衡力，该平衡力通过三腔动力液压缸活塞缸筒作用于身管，以实现身管的非平衡力补偿；通过切换比例伺服阀的进出油方向将其切换到身管抬升状态，液压油流入三腔动力液压缸上腔，液压油通过三腔动力液压缸下腔流回油箱，此时三腔动力液压缸活塞缸筒对身管施加一个向上的作用力，从而驱动身管向上调转；通过切换比例伺服阀的进出油方向将其切换到身管下降状态，液压油流入三腔动力液压缸下腔，液压油通过三腔动力液压缸上腔流回油箱，此时三腔动力液压缸活塞缸筒对身管施加一个向下的作用力，从而驱动身管向下调转。

同源平衡及定位电液伺服系统框图如图2所示，平衡控制器比较压力传感器测量的平衡腔实际压力与期望压力的误差，根据压力误差计算出控制量作用于比例减压阀，从而控制平衡腔的压力，该压力通过缸筒活塞作用于身管负载，以主动平衡负载重力矩；定位控制器比较旋转变压器测量的身管实际位置与给定位置的误差，根据位置误差计算出控制量作用于比例伺服阀来控制进入上、下腔液压油的流量大小和方向，以实现火炮身管的定位控制。

图2 同源平衡及定位电液伺服系统框图

1.2 系统模型

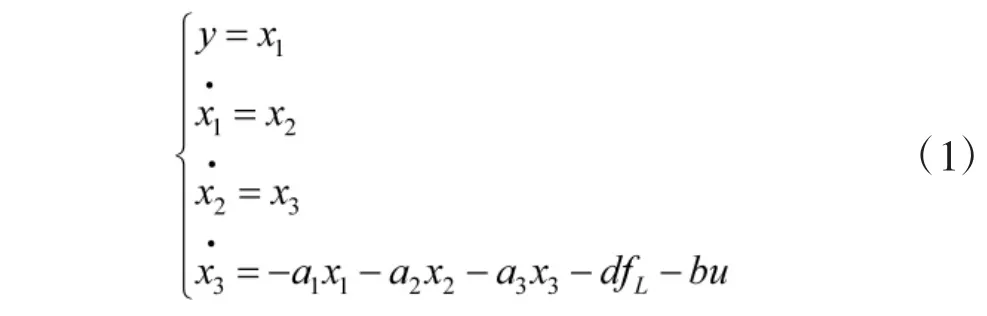
在工作过程中，将理想状态变量定义为：

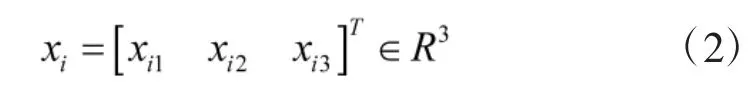
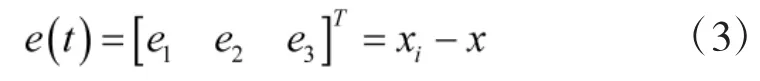
对电液伺服系统进行线性化假设，可以获得比较精确的非线性动力学方程。电液伺服系统的控制目标即为使实际状态x（t）时刻跟踪给定的理想状态xi（t），以保证跟踪误e（t）差趋近于零。

但在实际系统中存在很多变量随着工况的变化而变化，如系统泄漏系数Ct、油液粘性阻尼系数Bm、等效排量De和负载扰动TL等。且表现出强烈的非线性时变动态特征，即 a1、a2、a3、d、fL和 b 的参数具有时变性，因此，该系统属于非线性系统。

2 控制器设计

2.1 分数阶 PIλDμ控制器（FOPID）

研究分数阶系统经常采用算子离散化的方法对分数阶系统进行有理函数的离散化，其中离散方法主要分为两种方法，包括直接离散化方法和间接离散化方法。直接离散化利用z变换来近似，用一个有限阶次的函数去逼近z域的模型。

在频段（ωb，ωh）内，分数阶微分算子用 z变换近似，再用一个有限阶次的函数逼近z，由此可得Oustaloup滤波器为：

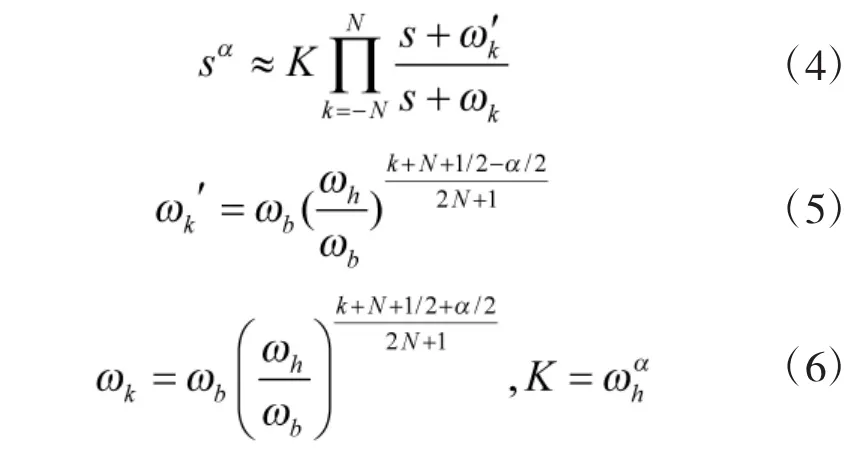
在近似求解的过程中引入合适的系数，使整个频段上有很高的准确性，同时也具有一定的实用性，这就是 Oustaloup改进算法。在频段（ωb，ωh）内分数阶微积分算子用一个分数阶模型K（s）来进行描述。令：

因此，可以得到：

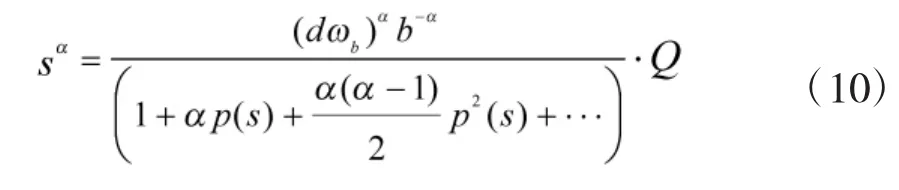
将Taylor级数进行剪切，剪切到一阶项得：

再将 p（s）带入可得：

用 Oustaloup 将 K（s）展开，可得：

这里2N+1为近似的阶次。该改进近似的具体算法如下：①选定频段和阶次；②利用α计算ω'k和ωk；③计算K；④计算出近似化的有理传递函数。

在一般情况下，高阶次近似是更准确的，但它也需要更长的时间。本文选取ωb=0.000 1，ωh=10 000，参数N=4。通过大量的实践和理论分析，当b=10，d=9时，改进的近似可以得到一个很好的近似结果。

Podlubny［11］教授最早提出分数阶 PIλDμ控制器，该控制器一般表示为 PIλDμ控制器，除了 Kp，Ki和Kd外，它还包括一个微分阶次λ和积分阶次μ，其传递函数为：

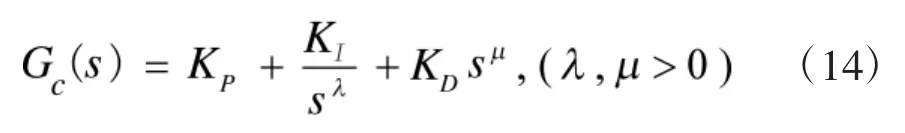
式（14）中，Kp为比例常数，Ki为积分常数，Kd为微分常数，微分阶次λ和积分阶次μ均为实数，控制信号u（t）在时域中可以表示为：

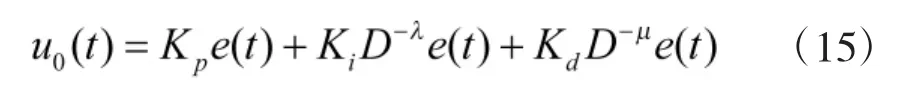
当λ=1及μ=1时，分数阶PID控制器即成为了整数阶PID，可见整数阶PID是分数阶PID控制器的一种特殊情况；当λ=0及μ=1时，分数阶PID就是PD控制器；当λ=1及μ=0时，就是PI控制器。

分数阶控制器是古典整数阶控制器的一般化，所有上述类型的PID控制器都是分数阶PIλDμ控制器的某一特殊情况。

图3 分数阶PIλDμ控制结构示意图

2.2 模糊PID控制器（Fuzzy-PID）

常规PID控制方法虽然能使系统具有良好的稳态性，但系统的鲁棒性和抗干扰能力不够理想［13］。模糊控制基于前人的经验和操作数据，具有较强的鲁棒性。图4所示为Fuzzy-PID控制结构框图。

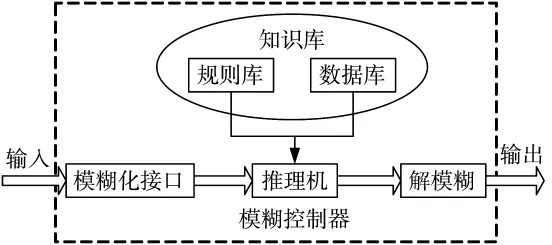
图4 模糊PID控制器（Fuzzy-PID）结构框图

在本文中，模糊控制和分数阶控制结合在一起，有效地解决了模糊控制存在的稳态误差缺陷，并拥有较强的鲁棒性。

2.3 模糊分数阶 PIλDμ控制器（Fuzzy-FOPID）

在同源平衡及定位电液伺服系统中，分数阶PIλDμ控制参数 Kp、Ki和 Kd作为输出语言变量，选取偏差e和偏差ec的变化率作为输入语言变量，输入变量e、ec和输出变量Kp、Ki和Kd的模糊子集均为{负大、负 中、负小、零、正小、正中、正大}，记为{NB、NM、NS、ZE、PS、PM、PB}，选取输入论域 e、ec为［-6，6］，输出论域 Kp、Ki和 Kd论域均为［0，1］。

由 e和 ec及 ΔKp、ΔKi、ΔKd积分阶次 λ 和微分阶次μ的模糊子集和论域，采用模糊推理设计出模糊分数阶PIλDμ参数模糊调整矩阵。表1～表3分别是Kp、Ki和Kd的模糊规则表。

表1 模糊控制规则（Kp）

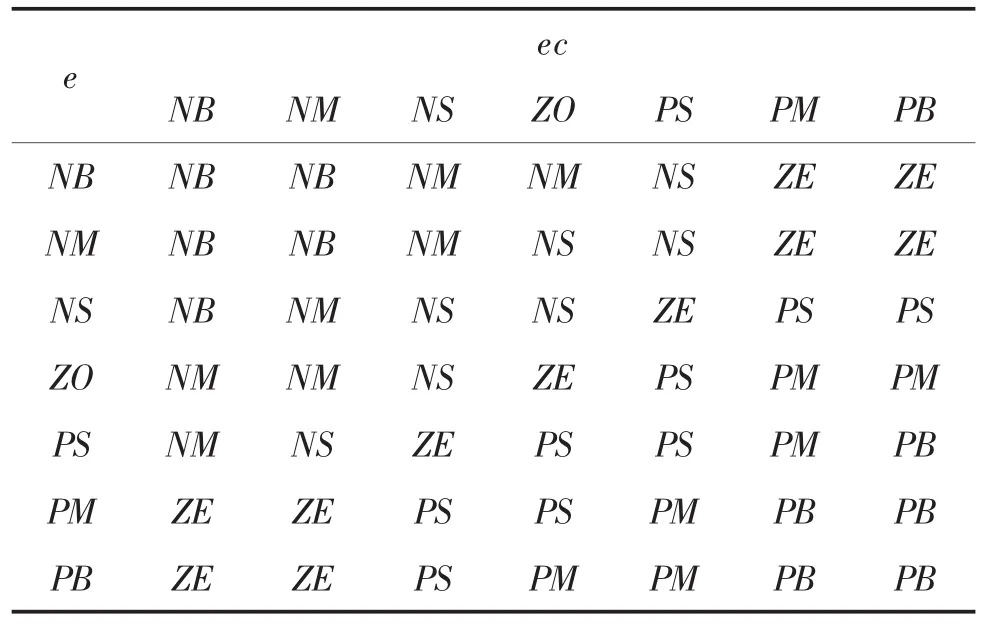
表2 模糊控制规则（Ki）

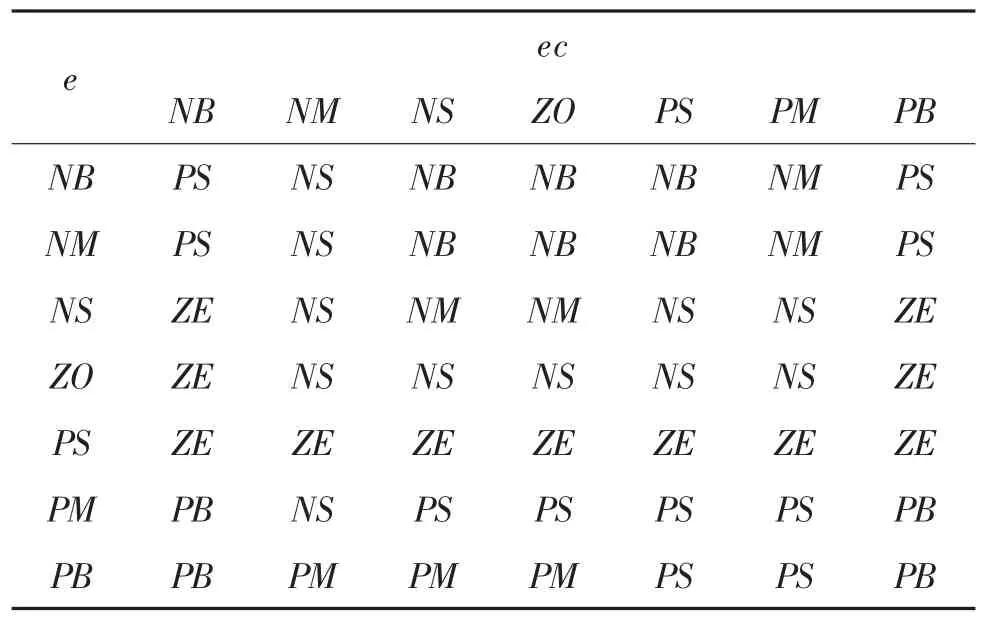
表3 模糊控制规则（Kd）

Kp、Ki和Kd的参数根据模糊规则表调整如下：

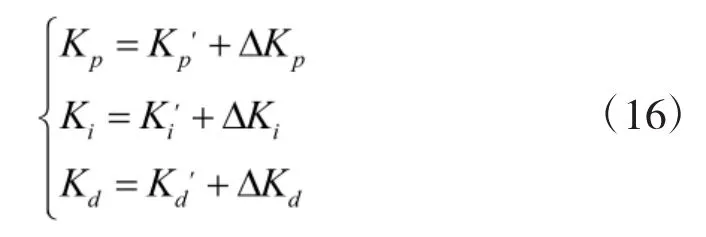
图5为模糊分数阶PID控制框图：

图5 Fuzzy-FOPID控制框图

Fuzzy-FOPID是FOPID通过模糊推理调整其比例增益Kp，积分常数Ki及微分常数Kd，从而优化整个控制系统。

3 仿真实验结果

为对比在实际工作系统中FOPID控制器与Fuzzy-FOPID控制器的效果，搭建半实物电液伺服系统仿真平台，该半实物仿真实验平台的主要参数为：J=155 000 Kg·m2，Ct=1.5×10-13（m3·s-1）/Pa，V0=0.011 781m3，βe=700 MPa。该电液伺服系统所选参数如下：ka=0.35 A/V，K1=1.96×10-3m3/（s·A），A=0.002 8 m2，V0≈V1，Bm=1 500 N·m/（rad/s），J=231.8 Kg·m2，V0=0.003 m3，G=9 870 Kg·m/rad，βe=700 MPa，Ct≈CL1，Ct=1.5×10-13（m3·s）/Pa，Qs1=20 L/min，k2=4.2×10-5，kq1=0.05 m2/s。

为了比较两种控制策略对外界负载扰动的鲁棒性，在t=8 s～10 s时加入幅值为2 KN·m方波扰动项。图6是系统在方波扰动时Fuzzy-FOPID控制器与FOPID控制器作用下的阶跃响应误差曲线。由图6可知，两种控制系统均无超调量，且进入±0.000 5 rad（≈±0.5 mil）误差带的时间均为 1.75 s。Fuzzy-FOPID控制系统偏离目标值的最大值为0.004 2rad，FOPID控制系统偏离目标值的最大值为0.02109rad，Fuzzy-FOPID具有较强的鲁棒性。

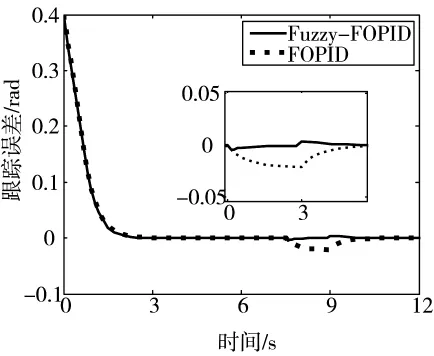
图6 方波扰动的阶跃响应误差曲线

图7给出了Fuzzy-FOPID控制下方波扰动跟踪值。由图可知，Fuzzy-FOPID控制系统对扰动的跟踪准确，且曲线平滑。

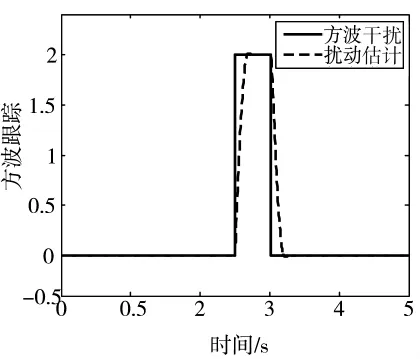
图7 方波扰动及其估计值

为进一步观察两种控制器性能，在该系统阶跃跟踪时叠加频率为0.5 HZ，幅值1 KN·m的正弦扰动，得到图8所示系统阶跃响应误差曲线，可知，FOPID控制下最大跟踪误差为0.019 9 rad，Fuzzy-FOPID控制策略下的最大跟踪误差则为0.002 438 rad，跟踪精度相比FOPID提高8.16倍，系统外部扰动得到有效抑制，Fuzz-FOPID控制性能更加突出，鲁棒性更强。

图9给出了正弦干扰状态下Fuzzy-FOPID控制下扰动估计值，Fuzzy-FOPID控制系统对扰动的估计较为准确。

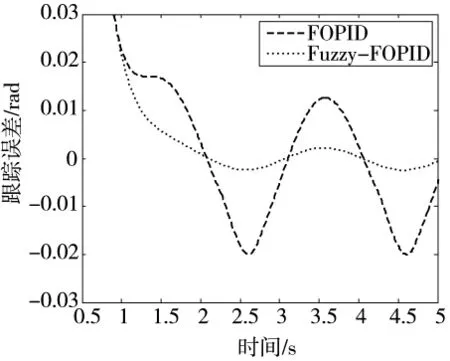
图8 正弦扰动阶跃响应误差曲线

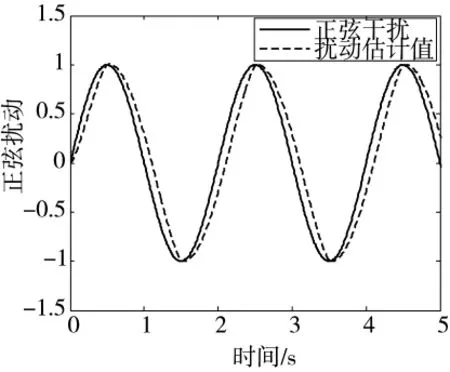
图9 正弦扰动及其估计值

图10是正弦干扰状态下非平衡力矩与平衡力矩的误差曲线，力矩误差曲线呈正弦变化，最大峰值力矩误差为13.07 Nm，系统外部扰动得到有效抑制，不平衡力矩的主动平衡补偿具有明显效果。

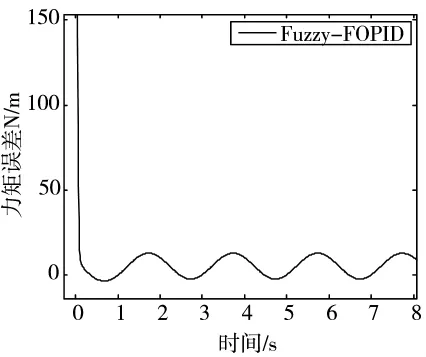
图10 正弦扰动力矩误差

4 结论

围绕Fuzzy-FOPID控制器的设计进行介绍，对FOPID、Fuzzy-FOPID两种控制系统进行分析。针对系统非线性扰动特征设计了基于Fuzzy的FOPID控制器，并通过半实物仿真实验测试系统的控制性能。结果表明：Fuzzy-FOPID控制系统在方波扰动作用时间内偏离目标的最大值是FOPID控制偏离最大值的0.2倍，Fuzzy-FOPID的跟踪精度相比FOPID提高8.16倍，因此，Fuzzy-FOPID控制器具有更强鲁棒性，解决非线性扰动的性能更加优越。

［1］PURDY D J.Comparison of balance and out of balance main battle tank armaments［J］.Shock and Vibration，2001（8）：167-174.

［2］COCUZZA S，PRETTO I.Novel reaction control techniques for redundant space manipulators Theory and simulated microgravity tests ［J］.Acta Astronautica，2011 （68）：1712-1721.

［3］GAO Q.A novel active disturbance rejection-based control strategy for a gun control system ［J］.Journal of Mechanical Science and Technology，2012（26）：4141-4148.

［4］李喆，李红丽，贺永利，等.基于DSP的永磁同步电机伺服系统实验平台设计 ［J］. 四川兵工学报，2015，36（3）：121-124.

［5］张海洋，申超，沈松波，等.某炮链条式弹簧平衡机设计计算［J］.火炮发射与控制学报，2009，30（1）：52-54.

［6］李自勇，戴田国，马大为，等新型火箭发射平台动力学仿真与优化研究［J］. 火炮发射与控制学报，2008，29（1）：39-41.

［7］张景华，余英，康瑞霞.大口径轻型牵引火炮关键技术［J］.火炮发射与控制学报，2010，31（1）：89-92.

［8］葛建立，过斌，杨国来.基于参数优化的炮塔轻量化设计［J］.火炮发射与控制学报，2011，32（4）：82-85.

［9］韩崇伟.火炮位置伺服系统的鲁棒控制与应用［D］.西安：西安交通大学，2002.

［10］黄丽莲，周晓亮，项建弘.分数阶PID控制器参数的自适应设计［J］.系统工程与电子技术，2013，35（5）：1064-1069.

［11］梁涛年，陈建军，王媛，等.分数阶系统模糊自适应PID控制器 ［J］. 北京工业大学学报，2013，39（7）：1041-1045.

［12］ PODLUBNY I.Fractional differential equations［M］.SanDiego：Academic Press，1999：41-117.

［13］张乐，吴金男，毕少杰.基于模糊PID的直升机模型飞行姿态控制［J］.控制工程，2014，21（3）：387-390.

A Homologous Balance and Positioning Servo System of Fuzzy Fractional Order PID Control

SUN Hao1，GAO Qiang1，LIU Guo-dong2，HOU Yuan-long1，TANG Qiao-ge1
（1.School of Mechanical Engineer，Nanjing University of Science and Technology，Nanjing 210094，China；2.North Automatic Control Technology Research Institute，Taiyuan 030006，China）

For a homologous balance and position electro-hydraulic servo system，a fuzzy fractional order PID controller is designed.By using fuzzy rules to regulate the parameters of fractional order PID controller，the system can be into a stable state quickly.At the same time，the response speed and robustness of the system can be improved.Thus，the fuzzy fractional order PID controller has a better control performance than fractional PID controller.Hardware in the loop （HWIL）simulation experiment is designed and shows that the fuzzy fractional order PID controller is better than fractional order PID controller in terms of response speed，overshoot and steady-state error，and especially robustness of external load disturbances.

homologous balance and position，fuzzy fractional order PID controller，electro-hydraulic servo system

TP273

A

10.3969/j.issn.1002-0640.2017.07.014

1002-0640（2017）07-0061-05

2016-05-18

2016-07-16

国家青年科学基金资助项目（51305205）

孙 浩（1990- ），男，河南淮阳人，硕士研究生。研究方向：智能检测与控制。