基于挠度公式的重力坝水平位移监测模型水压分量的校验

易恒如，王东，2，李乾德，陈玲，谢鑫

（1.四川大学水利水电学院，四川成都，610065；2.四川大学水力学与山区河流开发保护国家重点实验室，四川成都，610065）

基于挠度公式的重力坝水平位移监测模型水压分量的校验

易恒如1，王东1，2，李乾德1，陈玲1，谢鑫1

（1.四川大学水利水电学院，四川成都，610065；2.四川大学水力学与山区河流开发保护国家重点实验室，四川成都，610065）

对宝珠寺大坝17号和22号坝段顺流向水平位移监测资料进行统计回归分析，得到模型的回归方程及各影响分量，同时使用挠度理论公式验证了其中水压分量的精度。此分析方法对于重力坝变形监测模型中水压分量的精度校验、乃至确定相关项目的监控指标，有借鉴和参考意义。

挠度；重力坝；监测模型；水压分量；精度校验

安全监测与分析评价是贯穿大坝建筑生命周期的重要使命，影响混凝土重力坝变形的最主要因素——气温和库水位是一种客观存在，传统大坝监测安全评价中，运用统计回归方法将这些影响效应定量解析、剥离开来，剩下时效分量用来评价大坝的健康状况。为了确保这些定量分析中获得真正的“工程解”，需要对解析的各个分量进行分析评价。比如，对于一个典型混凝土重力坝段，回归分析成果里，各影响分量的解析是否准确？水压、气温等影响因素对其变形效应各占多少比例？准确回答这些问题实属不易。

结合宝珠寺大坝典型坝段的水流向水平位移监测资料，对影响大坝变形的相关响应机制展开分析，同时采用挠度理论公式对水平变位监测模型中的水压分量进行校验。

1 工程概况

宝珠寺水电站位于四川省广元市境内，在嘉陵江水系白龙江干流下游。水库大坝为混凝土重力坝，最大坝高132 m，电站为常规坝后式，发电为主。水库正常蓄水位588 m，死水位558 m，防汛限制水位为583 m，水库总库容25.5亿m3，调节库容13.4亿m3，为不完全年调节水库。坝基岩体主要为钙质粉砂岩和钙硅质粉砂岩，岩石强度高，岩体断裂虽较发育，但规模小，岩体强度较高，风化不严重，渗透性中等。

17号坝段水平变位从初期蓄水开始监测，22号坝段水平变位是蓄水稳定后的2000年初实施监测，两典型坝段变形及上游水位见图1，简化剖面见图2。

2 变形监测模型及分析评价

2.1 模型构建

大坝安全监测分析模型有统计模型、理论模型和混合模型，其中统计模型在工程实践中运用最广泛、最成熟。统计模型构建的核心方法是回归分析，回归分析则是研究不存在确定性关系的变量之间规律性的一种数学方法。

图1 宝珠寺水电站历年上游水位及典型坝段水平变位过程线图Fig.1 Graph of upstream water level and horizontal displacement of typical dam sections of Baozhusi hydropower station

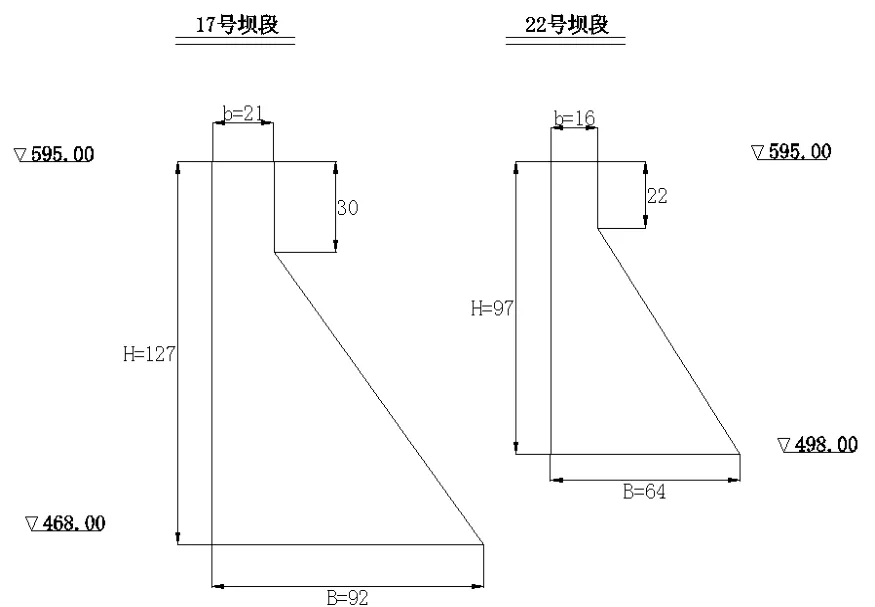
图2 17号和22号坝段剖面简图Fig.2 Cross section of dam sections No.17 and No.22

影响大坝变形的因素有水位、温度和时效[1]。就宝珠寺水电站而言，其坝前水位及坝区气温的周期性变化较为明显，且对大坝变形呈现出一定滞后效应。初蓄期水位从下闸前的河床天然水位开始，在短期内屡创新高、急剧上涨，其过程区别于后期常年周期水位特征，传统常规模型不足以刻画这一特征，因此在常规模型水压分量中加入“新高水位因子”[2]，若当日水位超过前次最高水位，入选该因子。因此，变形监测统计数学模型中，取效应分量为水压及新高水位因子、温度、时效，其模型可构造为如下形式[3]：

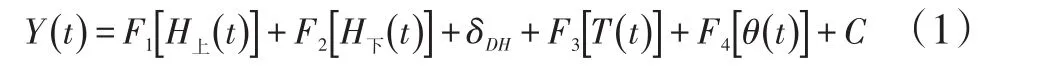
式中，Y(t)：变形监测值在时间t的统计估计值；

δDH：新高水位因子,包含两项：当日水位超过上一测次及之前的最高水位的差值DH1以及DH1与当日水位之积DH2,对于“新高水位因子”，超出量越大、超出部分所处高程越高，则对效应量的影响也就越大，这种刻画方式符合初蓄期水位急升过程的效应量响应特征；

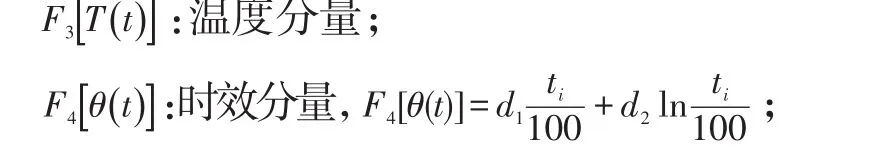
C：待定常数项，包含各分量中的常数项。

上述模型中各分量的函数形式主要通过相关理论及类似工程经验拟定。按上述模型，根据大坝变形测值序列进行回归分析，即可确定模型各参数。

2.2 回归分析及评价

用上述模型回归分析17号和22号坝段水平变位，成果见表1、表2和图3～6。

两典型坝段的复相关系数均大于0.94，初步判定回归方程有效。分析各分量的工程规律特征，先将时效分量加常数项，使之从0开始变化，由于温度分量本身就是相对起测时间当天温度的，所以常数项为0，水压分量的常数项见图5和图6，各分量变幅及其占比见表2。

由以上成果可见，各效应分量变化过程符合重力坝相关的力学、热学规律；两坝段水压分量所占的比例接近，均超过65%，是主要影响因素；时效分量因两坝段起测时间不同而呈现合理的特征差异；温度分量变幅值存在显著差异的原因是两坝段的高度及坝顶宽度不同。所以可认为本统计模型在工程精度范围内是合理的。

3 挠度理论验证水压分量

根据上述成果进一步展开分析，以变截面倒置

悬臂梁挠度公式计算水压力下的大坝变形理论值，将其与统计回归水压分量值对比，来验证其精度。取大坝的1 m单宽，挠度公式如下[4]：

表1 17号和22号坝段坝顶水平位移回归参数表Table 1 Regression parameters of horizontal displacement of dam sections No.17 and No.22

表2 顺流向水平位移各分量变幅Table 2 Variation amplitude of each component of horizontal displacement along the river

图3 17号坝段回归值与实测值比较Fig.3 Comparison between regression value and measured value of dam section No.17

图4 22号坝段回归值与实测值比较Fig.4 Comparison between regression value and measured value of dam section No.22

图5 17号坝段回归方程各分量对比图Fig.5 Comparison of each component in regression equation for dam section No.17

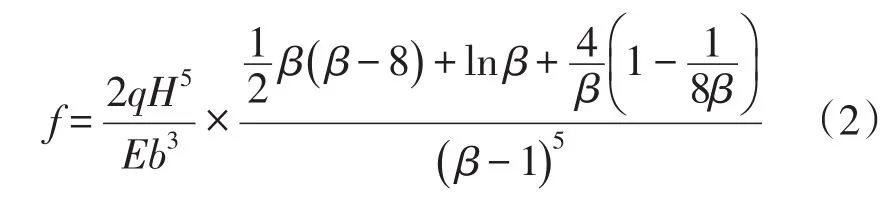
图6 22号坝段回归方程各分量对比图Fig.6 Comparison of each component in regression equation for dam section No.22

式中：E是材料弹性模;β是上下宽度之比B b，而H、B、b各参量见图2所示。

取实测水位过程为边界条件代入公式，获得挠度值过程线，并与实测变形数据的水压分量进行对比。对于22号坝段，由于起测时点并非大坝投运时间，其变形数据为相对于起测时点的相对值，而挠度理论值为绝对值，所以将其回归分量加上常数，使起测时点的值与理论值相同，再行对比，如图7、图8和表3所示。

从上述成果可见，理论值与回归水压分量值近似重合，只在部分峰值略微有差异，尽管二者的总变幅略有差距，但其均值及波动规律非常接近，表明统计模型的水压分量有足够的精度。

4 结语

图7 17号坝段理论值与回归值对比Fig.7 Comparison between theoretical value and regression value of dam section No.17

图8 22号坝段理论值与回归值对比Fig.8 Comparison between theoretical value and regression value of dam section No.22

随着我国大坝安全管理的进步，越来越多的项目要求研究监控指标，开展智能安全监测。传统上，监控指标的确定多数是基于统计回归成果，那么统计回归成果的质量和精度就显得越来越重要。用挠度理论公式很好地验证并改进（分量常数项的分配和确定）了宝珠寺重力坝典型坝段水平位移统计模型水压分量的精度，分析方法对于监测模型的精度校验乃至确定相关项目的监控指标有参考意义，但使用中须注意某些测值的相对性，及其与理论值之间的差异。■

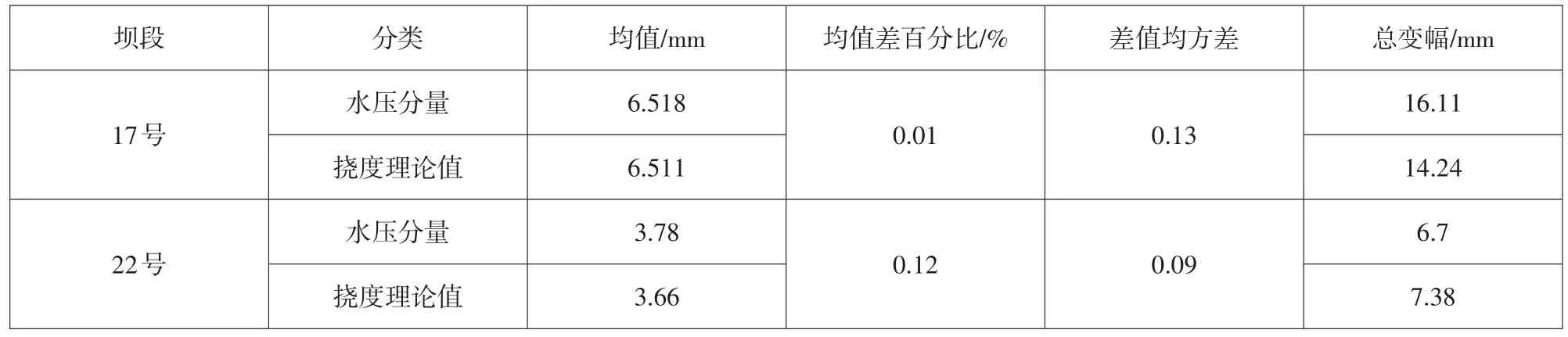
表3 回归水压分量值与扰度理论值对比Table 3 Comparison between theoretical values of hydraulic pressure components and theoretical deflection value

[1]谢孟，黄家鸣.变截面悬臂梁的挠度计算[J].四川建筑科学研究，1992(2)：31-33.

[2]陈建康,王东,李艳玲,等.宝珠寺水电站大坝变形及内观仪器监测资料分析[R].四川大学水利水电学院,2007.

[3]胡明秀,邓勇,王东,等.包含新高水位因子的重力坝垂直位移统计模型[J].大坝与安全,2012(1)：50-53.

[4]吴中如,沈长松,阮焕祥.论混凝土坝变形统计模型的因子选择[J].河海大学学报,1988,16(6)：1-9.

Verification of hydraulic pressure component in horizontal displacement monitoring model for gravity dam based on deflection formula

YI Heng-ru,WANG Dong,LI Qian-de,CHEN Ling and XIE Xin//School of Water Resource&Hydropower Engineering,Sichuan University

Regression analysis on the horizontal displacement monitoring data of dam sections No.17 and No.22 of Baozhusi dam is carried out.The regression equation and influence components are obtained.At the same time,the accuracy of hydraulic pressure component is verified by application of deflection theory formula.The analysis method can be used for calibration of the hydraulic pressure components in deformation monitoring model for gravity dam,as well as for the determination of monitoring indexes for similar projects.

deflection;gravity dam;monitoring model;water pressure component;accuracy check

TV698.1

B

1671-1092（2017）03-0032-05

2017-01-04；

2017-05-11

四川省科技支撑2014FZ0043

易恒如（1993-），女，湖北广水人，硕士研究生，研究方向为水利工程和坝工安全监测。

作者邮箱：584540842@qq.com