热力参数随温度变化导致的双金属标误差分析

方卫华,杜智浩，谭晨光

（1.水利部南京水利水文自动化研究所，江苏南京，210012；2.水利部水文水资源工程技术研究中心，江苏南京，210012；3.河海大学水利水电学院，江苏南京，210098）

热力参数随温度变化导致的双金属标误差分析

方卫华1，2，3,杜智浩3，谭晨光1

（1.水利部南京水利水文自动化研究所，江苏南京，210012；2.水利部水文水资源工程技术研究中心，江苏南京，210012；3.河海大学水利水电学院，江苏南京，210098）

为了解热力耦合条件下由于温度引起的热力参数变化带来的双金属标轴向误差，根据弹性力学理论推导了积分公式。根据相关文献确定的地表和深部温度，选择3个典型地区30 m、50 m和100 m不同深度的双金属标，计算了各种情况下由于温差导致的双金属标轴向误差。研究表明，即使对于100 m长的双金属标，由于弹性模量温度效应引起的最大测量误差都在10-2mm数量级，完全可以忽略不计。

双金属标；弹性模量；线膨胀系数；温度变化

0 引言

双金属标沉降监测是水准测量中的重要设施，具有测值直观和原理简单等优点。随着深厚覆盖层和高坝的不断兴建，双金属标的深度也在不断增加。文献[1]从工作原理、管材的选择和参数测定、结构型式、安装埋设、观测与计算等几个方面分析和探讨了双金属标应用中应注意的几个问题。文献[2]给出双金属标计算公式推导以及在缺少膨胀系数时双金属标钢管和铝管的线膨胀系数的求解方法。上述文献对规范双金属标的应用起到了很好的推动作用。实际上，双金属标不仅存在温度变形，而且温度变化将会使材料的弹性模量和线膨胀系数两个热力参数发生变化，从而导致在轴向重力作用下，轴向变形发生变化[3-5]。但上述文献以及相关标准[6]均未对温度变化导致热力学参数诱导的相关误差进行说明。随着双金属标杆长度的增加，这种影响是否可以忽略？目前尚未见相关文献报道，为此，笔者将在相关文献基础上对此进行研究，并给出明确结论。

1 基本假设及计算公式

以底部固定端为坐标原点，z轴向上为正方向。根据弹性力学，竖直放置的圆柱形杆由于重力引起的轴向变形为[5]：

假设温度在z方向上线性变化，由于温度变化导致弹性模量变化条件下，竖直放置的圆柱形杆在重力作用下的轴向变形为[5]：

式（1）、（2）中，g为重力加速度，K=kβ；k为温度由双金属底部到顶部的变化斜率，根据相应深度地下和地面温度进行计算，相关温度查文献获得，沿z轴温度变化为ΔT=kz，β为E随温度折减系数；H为双金属标杆长度。

杨氏弹性模量随温度变化可以表示成E(T)=E0(1-βT)，其中T为相对温度变化，E0为不考虑弹性模量变化情况下或基准温度时的弹性模量。假设由双金属底部到顶部的温度变化为线性变化，其斜率为k，由式（1）和（2）得到单根管柱由弹性模量的温度影响引起的误差为：

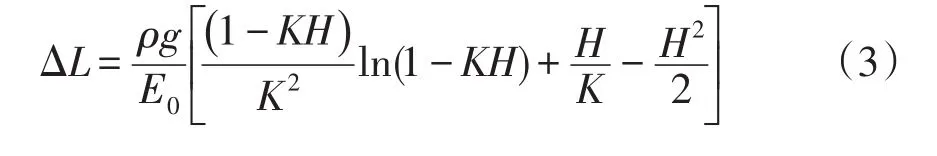
2 典型计算结果

依据文献[7]，分别选取新疆乌鲁木齐、山东济南和广东广州三个典型区域位置的城市浅层地温数据进行计算。根据文献[3]可知β=25α，其中α为金属的线膨胀系数。通过查阅《常用材料的线膨胀系数一览表》，可以得到碳素钢、铝在不同温度范围内的平均线膨胀系数值。ρ1、ρ2分别对应钢管和铝管质量密度，这里忽略其随温度的变化，取20℃时的值，E01、E02分别为基准温度下的钢管和铝管杨氏弹性模量，也取20℃时的值。相关固定参数见表1。

2.1 H=30 m情况

2.1.1 西部地区

以新疆乌鲁木齐地区为例，地下30 m深度的温度t2=11.6℃[7]。

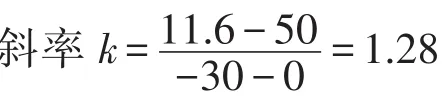
根据式（3）计算得到钢管：

铝管：

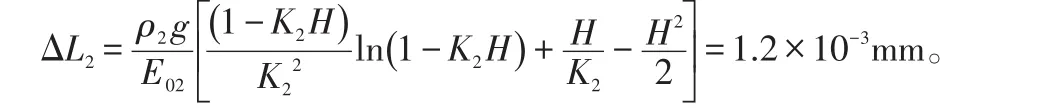
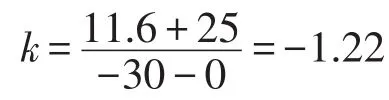
则钢管的线膨胀系数取碳素钢在-50～20℃之间的平均线膨胀系数α3=10.39×10-6/℃，铝管的线膨胀系数取α4=20.79×10-6/℃。相关参数见表3。

表1 固定参数表Table 1 Fixed parameters

表2 H=30 m时西部地区夏季参数取值表Table 2 Parameters value of summer in western area as H=30 m

则钢管ΔL3=-5.3×10-4mm，铝管ΔL4=-1.04× 10-3mm。

2.1.2 东部地区

以山东济南地区为例，地下30 m深度的温度t2=16.5℃[7]。

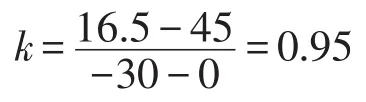
则钢管ΔL1=4.45×10-4mm，铝管ΔL2=8.96× 10-4mm。

则钢管ΔL3=-5.55×10-4mm，铝管ΔL4=-1.09× 10-3mm。

2.1.3 南部地区

以广东广州地区为例，地下30 m深度的温度t2=23.94℃[7]。

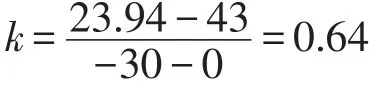
则钢管Δ L1=3×10-4mm，铝管Δ L2=6.01× 10-4mm。

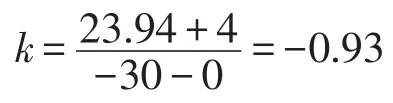
表3 H=30 m时西部地区冬季参数取值表Table 3 Parameters value of winter in western area as H=30 m

表4 H=30 m时东部地区夏季参数取值表Table 4 Parameters value of summer in eastern area as H=30 m

表5 H=30 m时东部地区冬季参数取值表Table 5 Parameters value of winter in eastern area as H=30 m

则钢管ΔL3=-4.19×10-4mm，铝管ΔL4=-8.32× 10-4mm。

2.2 H=50 m情况

2.2.1 西部地区

以新疆乌鲁木齐地区为例，地下50 m深度的温度t2=11.86℃[7]。

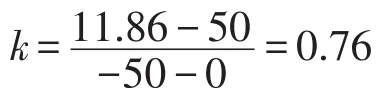
则钢管ΔL1=1.63×10-3mm，铝管ΔL2=3.26× 10-3mm。

则钢管ΔL3=-1.49×10-3mm，铝管ΔL4=-2.93× 10-3mm。

表6 H=30 m时南部地区夏季参数取值表Table 6 Parameters value of summer in southern area as H=30 m

表7 H=30 m时南部地区冬季参数取值表Table 7 Parameters value of winter in southern area as H=30 m

表8 H=50 m时西部地区夏季参数取值表Table 8 Parameters value of summer in western area as H=50 m

表9 H=50 m时西部地区冬季参数取值表Table 9 Parameters value of winter in western area as H=50 m

2.2.2 东部地区

以山东济南地区为例，地下50 m深度的温度t2=16.69℃[7]。

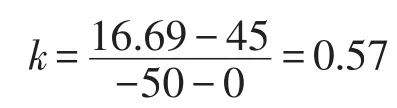
则钢管ΔL1=1.23×10-3mm，铝管ΔL2=2.49× 10-3mm。

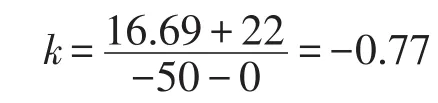
则钢管ΔL3=-1.55×10-3mm，铝管ΔL4=-3.04× 10-3mm。

2.2.3 南部地区

以广东广州地区为例，地下50 m深度的温度t2=24.31℃[7]。

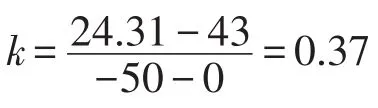
则钢管ΔL1=8.03×10-4mm，铝管ΔL2=1.61× 10-3mm。

表10 H=50 m时东部地区夏季参数取值表Table 10 Parameters value of summer in eastern area as H=50 m

表11 H=50 m时东部地区冬季参数取值表Table 11 Parameters value of winter in eastern area as H=50 m

表12 H=50 m时南部地区夏季参数取值表Table 12 Parameters value of summer in southern area as H=50 m

则钢管ΔL3=-1.19×10-3mm，铝管ΔL4=-2.37× 10-3mm。

2.3 H=100 m情况

2.3.1 西部地区

以新疆乌鲁木齐地区为例，地下100 m深度的温度t2=12.71℃[7]。

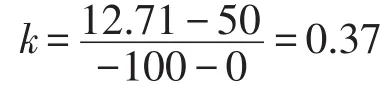
则钢管ΔL1=6.32×10-3mm，铝管ΔL2=1.27× 10-2mm。

则钢管ΔL3=-6.13×10-3mm，铝管ΔL4=-1.21× 10-2mm。

2.3.2 东部地区

以山东济南地区为例，地下100 m深度的温度t2=17.16℃[7]。

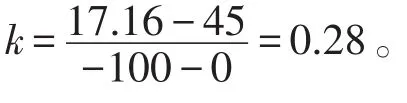
则钢管ΔL1=4.87×10-3mm，铝管ΔL2=9.8× 10-3mm。

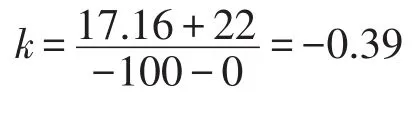
表13 H=50 m时南部地区冬季参数取值表Table 13 Parameters value of winter in southern area as H=50 m

表14 H=100 m时西部地区夏季参数取值表Table 14 Parameters value of summer in western area as H=100 m

表15 H=100 m时西部地区冬季参数取值表Table 15 Parameters value of winter in western area as H=100 m

则钢管ΔL3=-6.25×10-3mm，铝管ΔL4=-1.24× 10-2mm。

2.3.3 南部地区

以广东广州地区为例，地下100 m深度的温度t2=25.22℃[7]。

则钢管ΔL1=3.12×10-3mm，铝管ΔL2=6.24× 10-3mm。

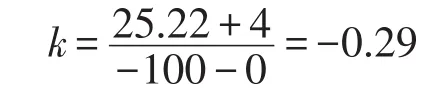
则钢管ΔL3=-4.84×10-3mm，铝管ΔL4=-9.64× 10-3mm。

表16 H=100 m时东部地区夏季参数取值表Table 16 Parameters value of summer in eastern area as H=100 m

表17 H=100 m时东部地区冬季参数取值表Table 17 Parameters value of winter in eastern area as H=100 m

表18 H=100 m时南部地区夏季参数取值表Table 18 Parameters value of summer in southern area as H=100 m

表19 H=100 m时南部地区冬季参数取值表Table 19 Parameters value of winter in southern area as H=100 m

3 结语

根据弹性力学和热力耦合相关理论，对深长双金属标温度变化引起热力参数变化的误差进行了计算分析。通过多个典型地点和多个深度双金属标温度误差计算，得到的误差范围在3×10-4～1.27× 10-2mm之间，表明温度变化导致热力参数变化引起的误差最大也是在10-2mm量级别，可以忽略不计。■

[1]赵花城,张琼.双金属标应用中的几个问题探讨[J].大坝与安全,2012(2)：14-19.

[2]刘满江.双金属标工作原理及线膨胀系数比的反演[C].工程安全监测技术,2007：357-360.

[3]徐志东,范子亮.金属材料的弹性模量随温度变化规律的唯象解释[J].西南交通大学学报,1993(2)：87-92.

[4]操龙飞.金属材料的热膨胀特性研究[D].武汉：武汉科技大学,2013.

[5]胡鹏浩.非均匀温度场中机械零部件热变形的理论及应用研究[D].合肥：合肥工业大学,2001.

[6]GB/T 4339-2008,金属材料热膨胀特征参数的测定[S].

[7]王贵玲,刘峰,王婉丽.我国陆区浅层地温场空间分布及规律研究(一)[J].供热制冷,2015(2)：52-54.

[8]阿帕尔,叶尔克江,冯俊平.昌吉市地温与气温关系初探[J].沙漠与绿洲气象,2007,1(3)：53-56.

[9]姜会飞,廖树华,叶尔克江,等.地面温度与气温关系的统计分析[J].中国农业气象,2004,25(3)：1-4.

Error analysis of double-metal marks caused by temperature variation on thermal parameters

FANG Wei-hua,DU Zhi-hao and TAN Chen-guang//Nanjing Automation Institute of Water Conservancy and Hydrology

Thermal parameters vary with the temperature.In order to understand the axial error of double-metal marks which is caused by the change of thermal parameters under the condition of thermomechanical coupling,the integral formula is derived based on the theory of elasticity.According to the surface and deep temperature determined by relevant literature,double-metal marks of different depths (30 m,50 m and 100 m)in three typical areas are selected to calculate the axial error caused by temperature difference in all situations.Research shows that the maximum measurement error caused by temperature effect on elastic modulus is in the order of 10-2mm,even for the 100 m long double-metal marks, which can be ignored.

double-metal marks;elastic modulus;linear expansion coefficient;temperature variation

TV698.1

A

1671-1092（2017）03-0013-08

2017-04-24

山西省水利厅科研项目（2015OSW2）

方卫华（1972-），男，安徽省望江人，教授级高级工程师，河海大学水工结构专业博士学位，主要从事大坝安全监测、工程安全评价及水利信息化设计、新方法以及相关理论方面研究。

作者邮箱：18705162780@163.com