不同压力环境下不透明非碳化ABS材料的热解温度模型研究

康茹雪，胡杨慧，宗若雯,2*，支有冉

(1.中国科学技术大学火灾科学国家重点实验室，合肥，230026; 2.中国科学技术大学苏州研究院苏州城市公共安全重点实验室，苏州，215123; 3.南京工程学院机械工程学院，南京，211167)

不同压力环境下不透明非碳化ABS材料的热解温度模型研究

康茹雪1，胡杨慧1，宗若雯1,2*，支有冉3

(1.中国科学技术大学火灾科学国家重点实验室，合肥，230026; 2.中国科学技术大学苏州研究院苏州城市公共安全重点实验室，苏州，215123; 3.南京工程学院机械工程学院，南京，211167)

在不同热流强度下，利用智能步进低压实验仓对不透明非碳化聚合物材料丙烯腈-丁二烯-苯乙烯(ABS)在不同压力情况下的热解过程中的表面及背面温度进行了实时测量，建立了表面吸收一维热解模型，预测了ABS在不同外界热流密度下，不同压力环境下表面温度及背面温度随时间的变化；并将实验测量值与模型模拟值进行对比。结果表明，非碳化聚合物的表面吸收一维热解模型在高热流密度下对温度的预测情况优于在低热流密度下对温度的预测结果，总体来说，模拟计算结果与实验测量值较为一致。

一维热解模型；环境压力；表面温度；背面温度

0 引言

大部分常用的聚合材料含有大量C、H原子，导致其有很高的易燃性和火灾危险性[1]。因此，对聚合物进行燃烧行为研究是非常必要的。热解是聚合物气化和其他热化学转化过程的第一步[2]，热解模型的研究对预测聚合物材料热解行为有着重要意义。

固体非碳化聚合物热解会发生在环境压力低于标准大气压的环境、高纬度地区以及飞机和航天器上。高海拔地区的环境压力，如中国拉萨(海拔高度3650 m)，环境压力大约为67 kPa，比标准大气压(101 kPa，21%O2)低34%。在飞机和航天器里，压力也要低于常压[3,4]。压力在聚合物热解气化阶段和热表面对流热损失方面都有影响，但目前大多数研究着重于真空或标准大气压下的聚合物热分解过程[5],针对聚合物的低压热解行为研究少之又少。

为了研究黑色非碳化聚合材料低压热解过程，对其建立热解模型是必不可少的。火灾动力学模拟模型FDS[6]，ThermaKin[7]采用有限的热解反应速率来模拟材料的热解过程，此类模型允许材料在一定温度范围内发生热解，热解反应用一个或多个反应方程来表征，材料内部热解产生的挥发分对总失重速率有影响。其控制方程为有源项的传热方程，质量方程为表征化学反应速率的阿伦尼乌斯公式。作为模型输入量的热动力学参数通过热重分析法(TG和DTG)在低热流强度范围内氮气气氛中得到[1,8-10]。关于聚合材料对辐射热流的吸收方式，普遍采用两种：表面吸收和深度吸收。前者认为材料对红外光谱不透明，所有外部辐射热均被样品表面吸收，或者认为材料为半透明介质，表面不吸收热量，所有热量均被材料内部吸收。在实际热解过程中两种吸收方式同时存在[11]。Jiang等[11]、Delichatsios等[12]对PMMA涂上黑色碳层，研究其在外加热辐射作用下的吸收方式，发现当材料的厚度为3 mm时，其透射率在0.03左右，当厚度大于4 mm时，其透射率接近为0。并且当外加辐射小于60 kW/ m2时，材料的吸收方式接近于表面吸收。Beaulieu和Dembsey[13]也发现外加热辐射热流大于60 kW/m2后，材料的质量损失和温度才会因为内部吸收的影响出现明显的非线性关系，并且对于黑色PMMA而言，表面有无黑色碳层涂料对其质量损失并无影响。通常情况下，在工程应用中为了简化计算，会将材料的吸收方式简化为表面吸收。为了研究低压下不透明非碳化材料的热解行为，在不同热流强度下，在智能步进低压实验仓内对不透明非碳化聚合物材料丙烯腈-丁二烯-苯乙烯(ABS)在不同压力情况下的热解过程中的表面及背面温度进行了实时测量，同时在实验数据的基础上，建立一维热解模型进行计算模拟，并将模拟结果与实验数据进行对比分析。本文假设黑色非碳化聚合材料对红外光谱为不透明，即外界辐射热量全部被材料表面吸收，再进一步通过热传导加热表面以下的材料[14-16], 建立了表面吸收一维热解模型，预测了不透明非碳化ABS在不同外界热流密度下，不同压力环境下表面温度及背面温度随时间的变化；并将实验测量值与模型模拟值进行对比。

1 实验方法及热解模型

1.1 实验方法

低压热解实验在中国科学技术大学火灾科学国家重点实验室智能步进式低压实验仓里进行，热解实验平台自行搭建，以模拟低压贫氧环境，氧气体积分数控制在4%～5%。低压热解试验台结构及实验平台结构示意图如图1。

黑色聚合物材料丙烯腈-丁二烯-苯乙烯(ABS)材料详细信息如表1所示。试验样品尺寸均为100 mm100 mm3 mm，为保证实验的一维性，样品四周及底部用铝箔纸进行包裹，为了防止材料热解过程中的热膨胀，纸上边沿高出样件表面10 mm。实验前分别在样品上下表面用铝箔纸固定直线0.5 mmK型热电偶来测量实验过程中的表面及背面温度，热电偶布置在样品对角线交点处。实验辐射源上方设置一根热电偶观察仓内温度变化情况。实验时，先用真空泵将密闭实验仓内的压力降至25 kPa，然后冲入氮气直到仓内压力升至101.25 kPa，之后重启真空泵，将仓内压力降至设计工作压力。本文中设计工作气压分别为35 kPa、65.2 kPa和98.1 kPa。 在实验前通过热流计标定所需辐射热流。在热流稳定之前，辐射源固定在实验仓导轨最左端，热流稳定后，利用滑块及重锤将辐射源拉至样品上方，每次实验保证样品置于辐射源中央。辐射源尺寸为300 mm300 mm，实验样品表面与辐射源底部之间的距离为40 mm，实验辐射热流分别为18 kW/m2及36 kW/m2。实验过程中低压实验仓内的压力会随着热解气的释放而发生微小变化，变化范围在1 kPa以内，仓内非热解区温度变化范围在4 ℃以内，因为压力和温度变化相对热解区温度和压力很小，因此假设实验过程中仓内压力及非热解区温度不变。实验工况如表2所示。

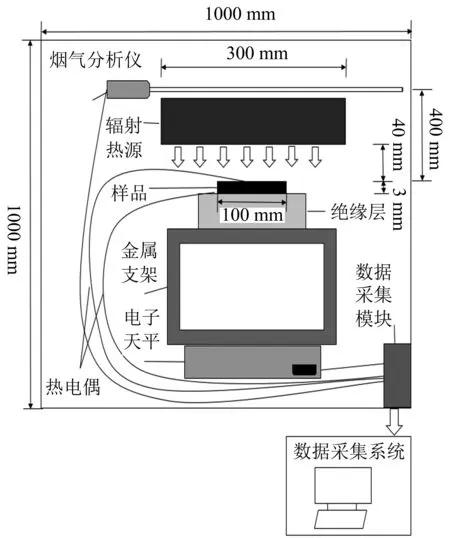
图1 低压热解实验平台Fig.1 Schematic of experimental setup

表1 样品详细信息

Table 1 Sample information

非碳化聚合物生产商商品名经销商ABS深圳安和达塑胶制品有限公司丙烯腈-丁二烯-苯乙烯共聚物深圳新诺实业塑胶材料有限公司

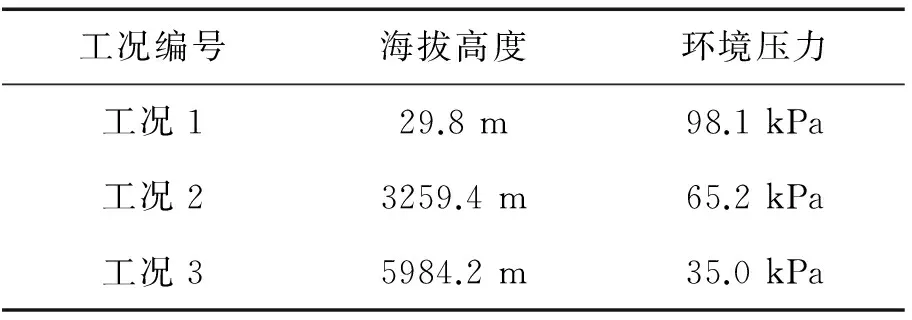
表2 实验工况汇总表

1.2 实验结果汇总

1.2.1 表面温度

图2为各热流密度下，样品表面温度随环境压力变化的变化情况示意图。由图2中可以明显看出，在两种热流密度下，表面温度随着环境压力的上升而下降。在低热流密度下，下降趋势明显，而在较高热流密度下，下降趋势则并不明显。这是因为低压会造成热对流系数的减小，从而减小对流热损失，增大样品表面的流入热量。

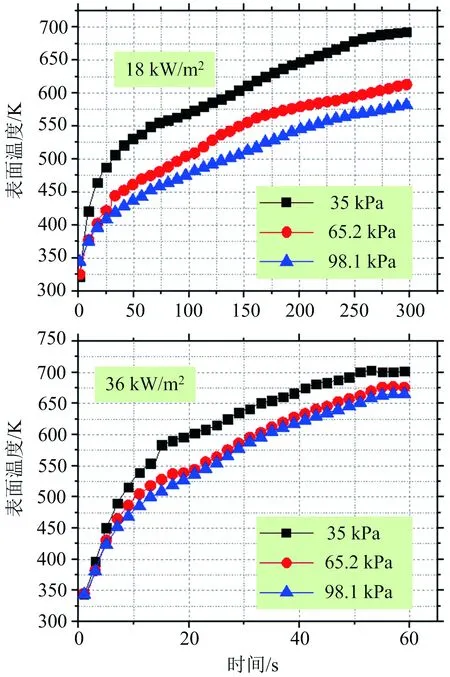
图2 不同环境压力下表面温度曲线图Fig.2 Profiles of the surface temperature under different gas pressures

1.2.2 背面温度

图3为各热流密度下，样品背面温度随环境压力变化的变化情况示意图。

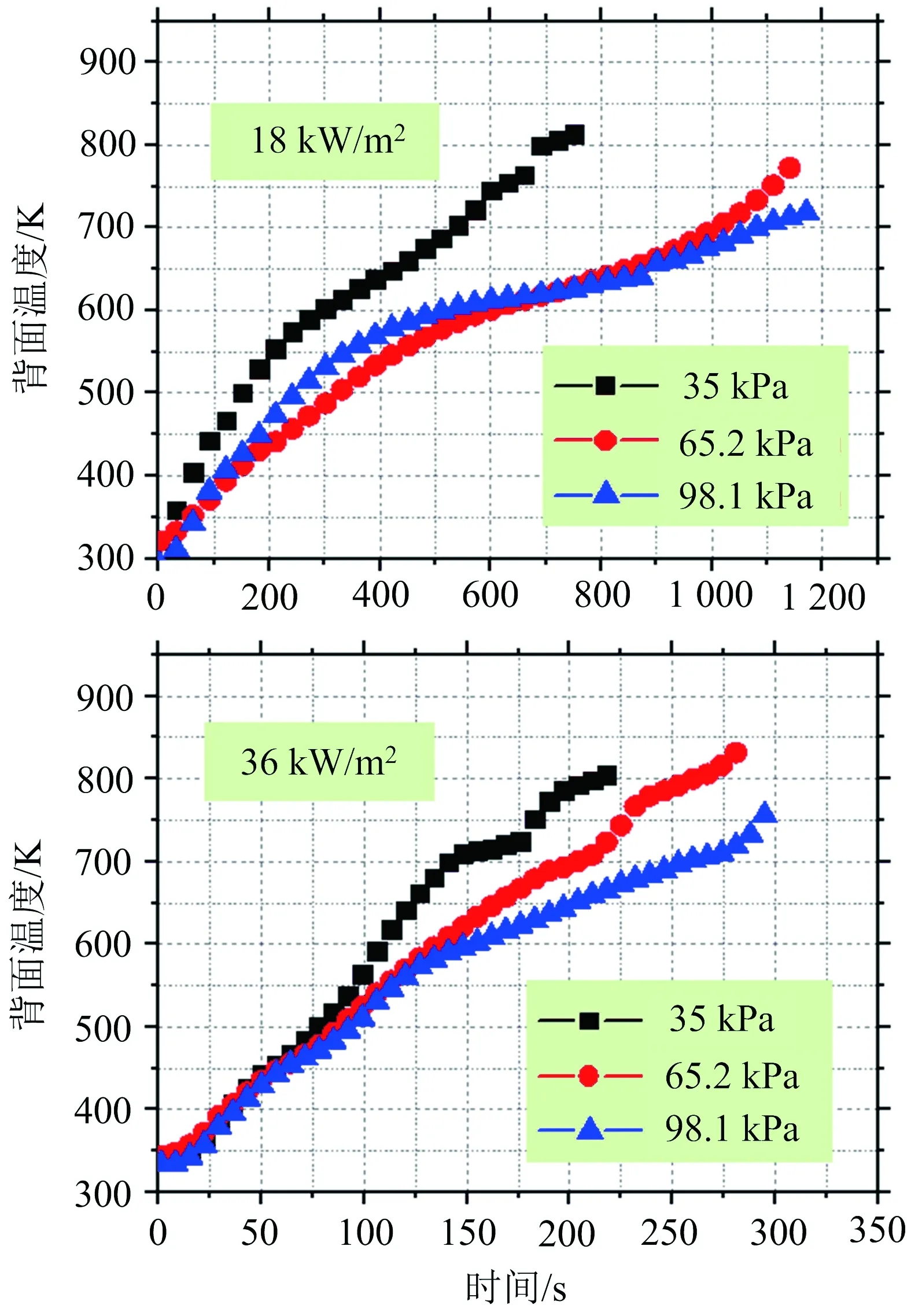
图3 不同环境压力下背面温度曲线图Fig.3 Profiles of the bottom temperature under different gas pressures

很明显，压力对背面温度的影响较小。背面温度对压力的敏感度没有表面温度对压力的敏感度高，这是因为在背面绝热的条件下，材料内部及背面对流热损失很小，在高热流下，甚至可以忽略不计。

1.3 基本热解模型

在实验基础上考虑材料内部传热及热解化学动力学反应，假设材料吸收方式为表面吸收，并通过控制方程建立一维热解模型，再耦合边界和初始条件对热解过程进行数值模拟，热解模型边界条件为背面绝热。为了简化模型，假设材料内部热解气体产生瞬间便逸出，且材料表面在热解过程中接收到的热流不变。相应地物理模型如图4所示。

图4 一维热解物理模型：背面绝热Fig.4 One-dimension pyrolysis model: Adiabatic bottom condition

1.3.1 控制方程

一维热解模型控制方程主要包括聚合物内能量守恒方程。假设黑色非碳化聚合材料热流吸收方式为表面吸收。则聚合物内部传热控制方程如下所示[17]。

ρsSv[ΔH+(TS-T

(1)

(2)

(3)

(4)

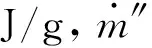
样品熔融后密度会发生变化[18]，

ρs=ρ0(1-βsΔt)

(5)

βs(T)=0.1995×10-6T2-

1.6178×10-5T-1.2271×10-2

(6)

其中，βs为ABS的热膨胀系数。

1.3.2 初始条件和表面控制体

初始条件为：

x=δpol:Ts(x,0)=T

(7)

x=0:T1-T2=0

(8)

其中，下标pol，分别指聚合物和环境值。

非碳化聚合物样品上表面控制体与空气接触且有传热传质过程，对上表面控制体应用能量平衡关系，可得能量平衡方程为：

h(Ts-T

(9)

Qout=

ρsSv[ΔH+(TS-T)(Cs-Cg)]

(10)

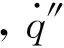
样品下表面边界绝热，因此下表面控制体能量平衡方程为：

ρsSv[ΔH+(TS-T

(11)

其中，h可通过自然对流经验公式算得，即热平板顶表面的自然对流公式为[17, 19]，由公式很明显看出，压力主要通过影响气体的热扩散系数从而影响热对流系数来影响流入样品热量：

(12)

其中：

(13)

(14)

(15)

(16)

其中，Ra为瑞利数，L为特征长度m，g为重力加速度m·s-2，比热容为常数，Cp,g=1.063 J·g-1K-1，导热系数(kg)、气体密度(ρg)、气体热膨胀系数(β)和动力粘度(νg)是温度的函数[20]：

kg(T)=1.5207×10-11T3-4.8574×10-8T2

+1.0184×10-4T-3.9333×10-4

(17)

(18)

(19)

νg(T)=-1.1555×10-14T3+9.5728×10-11T2

+3.7604×10-8T-3.4484×10-6

(20)

2 模拟结果与讨论

根据上述热解模型来计算ABS不同压力情况下的表面温度与背面温度，并与实验测量值进行对比。模型中的网格划分为0.1mm大小的均匀网格，时间步长为0.005s。在计算表面温度及背面温度之前，先对模型中的每个偏微分方程进行离散化处理，离散方法为显示差分法。根据离散化得到的离散化方程进行Matlab编程并求解计算。

2.1 输入参数

计算中用到的一些热物理参数如表3所示。

表3 模拟输入的ABS热物理参数汇总

2.2 模拟结果与对比

2.2.1 表面温度

表面温度是ABS热解过程中最直观的参数之一。在热解阶段的初期，热解反应主要发生在材料表面附近的一个薄层，因此热解速率的强烈程度在于表面温度的高低。图5～图6为不同压力情况，不同热流密度情况下，ABS表面温度实验值与模拟值的对比。其中Exp(Experiment)代表实验测得的表面温度，Sim(Simulation)代表模拟计算得到的表面温度。

图5 18 kW/m2辐射强度下ABS表面温度实验值与模拟值对比Fig.5 Comparison of experimental theoretical results of surface temperature of ABS under heat flux of 18 kW/m2

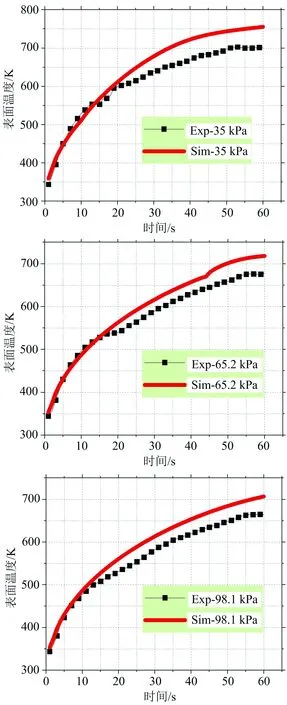
图6 36 kW/m2辐射强度下ABS表面温度实验值与模拟值对比Fig.6 Comparison of experimental and theoretical results of surface temperature of ABS under heat flux of 36 kW/m2

从图5、图6中可以看出，在高热流密度下，模型计算得到的表面温度与实验值较为接近。但是，在低热流密度下，模型计算的表面温度与实验值之间的差距较大，但在低压情况下，模拟值与实验值的一致性更好。在两种热流密度下，实验值均低于模型计算值。造成此种情况的原因可能是：1)模型假设为表面吸收，实际上还会有部分热量被材料内部吸收，导致实验值较低；2)模型内输入的材料热物理参数取自文献，与实际样品会有偏差；3)模型的边界条件与实际热解过程会有偏差；4)ABS受热会发生熔融，模型中仅考虑了材料热膨胀对热解造成的影响，有些因素未被完全考虑。低热流密度下，材料的热解速率较慢，因此相变的影响比较大，而高热流密度下，相变的影响较小。5)压力影响材料的热对流系数，导致低压下材料表面的流入热量较多，同时加快材料的热解速率，进一步减小了材料相变对模拟情况的影响。

2.2.2 背面温度

背面温度是ABS热解过程中另外一个非常直观的参数。图7～图8是不同压力情况，不同热流密度情况下，ABS背面温度实验值与模拟值的对比。

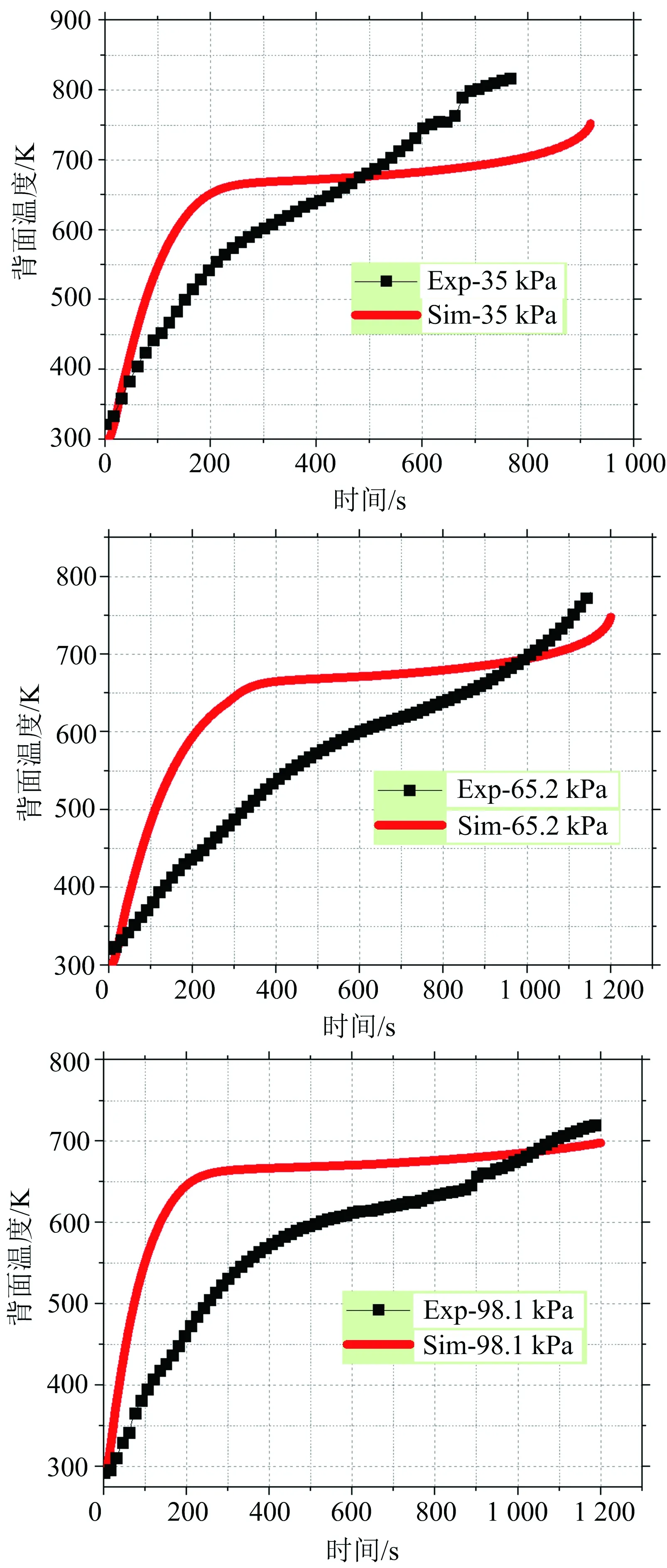
图7 18 kW/m2辐射强度下ABS背面温度实验值与模拟值对比Fig.7 Comparison of experimental and theoretical results of bottom temperature of ABS under heat flux of 18 kW/m2

低热流密度下ABS的大规模热解时刻可以从背面温度曲线反映出来，也就是材料经过初期温度迅速升高后到达拐点的时刻，该时刻之后材料背面温度缓慢升高，材料的净入能量通过热解损失了大部分。从图7和图8中可以很明显的看出，模拟值中拐点的出现较明显于实验值，这是因为在实际热解过程中，除过热传导吸收的热量，样品内部还会通过深度吸收得到一部分热量，这导致实际流入样品内部的热量要稍高于模型中流入的热量。热解初期模拟值的背面温度要稍高于实验值，这是因为模型假设为背面完全绝热状态，但是在实际的低热流热解情况中，背面的石棉板仍然会吸收一部分热量，导致材料背面的温度低于模拟值。高热流密度作用下的背面温度模拟结果同样好于低热流密度，这是因为低热流密度下，材料的热解不受热滞后效应的影响，所以热解的逐层热解效应稍弱。高热流密度下模拟值与实验值拐点的出现相比低热流密度下较为不明显，这是因为在高密度热流以及热滞后效应的双重作用下，样品底部通过对流，传导损失的热量微乎其微，因此材料的热解更接近与模型假设的逐层热解。此外，从图7、图8中可以看到，在两种热流密度下，常压下拐点的出现相较于低压较为明显，这也说明，压力导致的热对流损失对常压情况下的热解影响更大。

图8 36 kW/m2强度下ABS背面温度实验值与模拟值对比Fig.8 Comparison of experimental and theoretical results of bottom temperature of ABS under heat flux of 36 kW/m2

3 结论

开展了低压下不透明非碳化聚合物ABS的热解实验研究，对其热解过程中的表面温度和背面温度进行了实时测量，基于能量守恒，建立了表面吸收一维热解模型，预测了不透明非碳化ABS在不同外界热流密度下，不同压力环境下表面温度及背面温度随时间的变化，并将实验测量值与模型模拟值进行对比。主要结论如下：

1)实验过程中除了热传导，材料内部还会直接吸收部分辐射热，因此模拟结果会普遍高于实验值。此外，ABS的热物理参数和实验初始条件均与实验样品有误差，所以会影响模拟结果。高热流密度和低压情况下，因为对流热损失小，样品热解速率较快，所以压力和相变对样品的模拟情况影响较小，模拟值与实验值也较为接近。

2)总体来说，两种热流密度下，表面温度的实验值和模拟值较为一致。高热流密度下的模拟情况要好于低热流密度下，低压下的模拟情况要优于高压。

3)样品背面温度的实验值与模拟值也较为一致。在两种热流密度下，常压下拐点的出现相较于低压较为明显，表明压力导致的热对流损失对常压情况下的热解影响更大。

[1] Li J, Stoliarov SI. Measurement of kinetics and thermodynamics of the thermal degradation for non-charring polymers[J]. Combustion and Flame, 2013, 160(7): 1287-1297.

[2] Basile L, et al. Influence of pressure on the heat of biomass pyrolysis[J]. Fuel, 2014, 137: 277-284.

[3] Lange KE, et al.Bounding the spacecraft atmosphere design space for future exploration missions[R]. National Aeronautics and Space Administration, 2005.

[4] McAllister S, et al. Piloted ignition delay of PMMA in space exploration atmospheres[J]. Proceedings of the Combustion Institution. 2009, 32(2): 2453-2459.

[5] Koptelov AA, Karyazov SV. Effect of pressure on the thermal decomposition of polymers[J]. Doklady Physical Chemistry, 2003, 389(4): 101-105.

[6] Lautenberger C, et al. The application of a genetic algorithm to estimate material properties for fire modeling from bench-scale fire test data[J]. Fire Safety Journal, 2006, 41(3): 204-214.

[7] Stoliarov SI, Lyon RE. Thermo-kinetic model of burning for pyrolyzing materials[J]. Fire Safety Science, 2008, 9: 1141-1152.

[8] 苏诚伟, 等. 聚甲醛的热重分析研究[J]. 功能高分子学报, 1994, 7(2): 165-171.

[9] 曾文茹, 等. 非等温动力学积分-微分法研究聚苯乙烯热解反应机理及动力学参数[J]. 高分子材料科学与工程, 2006, 22(5): 162-165.

[10] 曾文茹, 等. 非线性等转化率法研究聚苯乙烯热解反应活化能与转化率的关系[J]. 高分子材料科学与工程, 2008, 24(8): 128-131.

[11] Jiang FH, et al. Absorption of thermal energy in PMMA by in-depth radiation[J]. Fire Safety Journal, 2009, 44(1): 106-112.

[12] Delichatsios MA, et al. Upward fire spread: key flammability properties, similarity solutions and flammability indices[J]. Fire Safety Science, 1991, 3: 217-226.

[13] Beaulieu PA, Dembsey NA. Flammability characteristics at applied heat flux levels up to 200 kW/m2[J]. Fire and Materials, 2008, 32(2): 61-86.

[14] Whiting P, et al. A one-dimensional mathematical model of laser induced thermal ablation of biological tissue[J]. Lasers in Medical Science, 1992, 7(1): 357-368.

[15] Staggs JEJ. Modelling thermal degradation of polymers using single-step first-order kinetics[J]. Fire Safety Journal, 1999, 32(1): 17-34.

[16] Delichatsios MA, Chen Y. Asymptotic, approximate, and numerical solutions for the heatup and pyrolysis of materials including reradiation losses[J]. Combustion and Flame, 1993, 92(3): 292-307.

[17] Incropera FP, et al. Fundamentals of heats and mass transfer[M]. John Wiley & Sons. Incorporation, 2007, 6.

[18] 黄永华, 等. 热膨胀系数简易测量装置研制及若干材料测量[J]. 化工学报, 2016, 67(S2): 38-45.

[19] Atreya A. Convection heat transfer, in SFPE handbook of fire protection[M]. Society of Fire Protection Engineers, 2016, 5.

[20] Gong JH, et al. A numerical study of thermal degradation of polymers: Surface and in-depth absorption[J]. Applied Thermal Engineering, 2010, 106:1366-1379.

[21] Li J, Stoliarov SI. Measurement of kinetics and thermodynamics of the thermal degradation for charring polymers[J]. Polymer Degradation and Stability, 2014, 106: 2-15.

[22] Li J, et al. Gasication experiments for pyrolysis model parameterization and validation[J]. International Journal of Heat and Mass Transfer, 2014,77: 738-744.

Pyrolysis temperature model of opaque non-charring ABS under different pressures

KANG Ruxue1， HU Yanghui1， ZONG Ruowen1, 2，ZHI Youran3

(1.State Key Laboratory of Fire Science, University of Science and Technology of China, Hefei 230026, China; 2. Suzhou Key Laboratory of Urban Public Safety, Suzhou Institute for Advanced Study, University of Science and Technology of China, Suzhou 215123, China; 3.Institute of Mechanical Engineering，Nanjing Institute of Technology Nanjing，Nanjing 211167, China)

A series of experiments on the opaque Acrylonitrile Butadiene Styrene (ABS) in reduced low-pressure chamber have been conducted in this work to study the pyrolysis of this polymer under different external heat fluxes. The variation of temperature at the surface and bottom of the sample during the whole process has been measured. A surface absorption one-dimension numerical model is developed to predict the surface and bottom temperature of ABS in a series of reduced pressures under different external heat fluxes. The model is verified by the measured experimental data. The results indicates that the theoretical result of temperature under higher heat flux is better than that under lower heat flux. The experimental results fit well with the theoretical results.

One-dimension pyrolysis model; Ambient pressure; Surface temperature; Bottom temperature

2016-12-22；修改日期：2017-02-27

国家自然科学基金面上项目(51576185，51606092)；国家重点研发计划(2016YFC0802101)；中央高校基本科研业务费专项资金(WK2320000034)

康茹雪(1992-)，女，陕西咸阳人。中国科学技术大学火灾科学国家重点实验室硕士研究生，安全科学与工程专业，主要从事聚合物热物理及烟气毒性等方面的研究。

宗若雯，E-mail：zongrw@ustc.edu.cn

1004-5309(2017)-00079-08

10.3969/j.issn.1004-5309.2017.02.03

X915.5

A