CRAM在放射性核素存量计算中的应用
张竞宇1 马亚栋1 陈义学1 高强2
CRAM在放射性核素存量计算中的应用
张竞宇马亚栋陈义学高强
1(华北电力大学核科学与工程学院 北京 102206) 2(环境保护部核与辐射安全中心 北京 100082)
在反应堆中,组成材料的稳定核素经受强中子辐照后,会被活化成放射性核素。这些核素及其衰变产物对工作人员的职业辐照剂量具有重要贡献。为了更好地进行人员的辐射防护工作,需要对放射性核素的存量进行精确计算。相对于核素平衡方程的其它求解方法,切比雪夫有理逼近方法(Chebyshev Rational Approximation Method, CRAM)在计算精度和效率方面具有综合性优势。首先介绍了CRAM的基本理论,随后选取典型的例题进行了测试验证。与解析解对比的结果表明,采用CRAM进行中子辐照下的核素活化衰变计算能够取得不错的效果,但是用于核素长期衰变计算可能导致计算错误。针对此问题,将收缩乘方技术与CRAM相结合,取得了正确的计算结果,拓展了CRAM的适用范围。
切比雪夫有理逼近方法,放射性核素,存量计算,收缩乘方
反应堆中存在很强的中子辐照,会导致结构材料的活化而使其具有放射性,当工作人员检查或维修反应堆中的管道或设备时,不可避免地会受到这些γ射线的辐照伤害。此外,结构材料在活化过程中会产生氢气和氦气,这些气体物质会对结构材料的强度造成损伤,其中的氚核素还具有很强的穿透性和放射性,容易对人员和环境造成危害。因此,需要特别关注放射性核素的存量计算问题,尽可能提高计算结果的准确性。
活化和衰变计算中涉及的核素种类多达上千种,并且不同核素的反应截面和半衰期差别很大,因此所对应的核素平衡方程在数学上具有大规模、强刚性的特点。对于此类问题的求解,学界经过长期的研究,开发了一系列的方法和程序,主要包括时间差分方法、线性子链方法和矩阵指数方法。
时间差分方法需要采用特殊处理才能提高计算效率。例如FISPACT-2007程序预先将短寿命核素从系数矩阵中移出以降低矩阵的病态性,再采用显式的指数欧拉方法基于大步长求解仅含有长寿命核素的方程,最后通过“平衡假设”近似计算短寿命核素,该方法的计算速度较快,但是由于采用了近似处理,在计算初期会有一定误差。
线性子链解析(Transmutation Trajectory Analysis, TTA)方法的基本原理是将复杂反应链分解成独立的线性反应链,再解析求解,以避免直接处理强刚性方程,目前已用在以CINDER程序为代表的多个程序中。该方法求得的解析解精度很高,但是反应链线性化过程比较繁琐使得整体效率较低,对此吴明宇等采用回溯算法自动进行反应链搜索,一定程度上提高了计算效率。
矩阵指数方法将对核素平衡方程的求解转化为对矩阵指数的计算,目前计算矩阵指数的方法主要基于数值逼近理论,代表程序有基于泰勒展开多项式逼近方法结合短寿命核素特殊处理的ORIGEN程序、基于切比雪夫有理逼近方法(Chebyshev Rational Approximation Method, CRAM)的SERPENT程序燃耗模块和DEPTH程序。其中,CRAM凭借无需对短寿命核素进行单独处理、在较大的时间步长下仍能得到很高的计算精度等优点而被广泛推荐。
1 切比雪夫有理逼近方法
对于含有种核素的材料,在中子辐照下,其核素平衡方程如下:

式(1)可以写成如下的矩阵形式:

式中:为系数矩阵。
采用矩阵指数方法求解式(2),解的形式如下:

根据文献[9]的观察,系数矩阵的特征值分布在复数平面的负实轴附近。此时,CRAM是指数函数在(‒∞, 0]区间的最佳有理逼近,如式(4)所示:
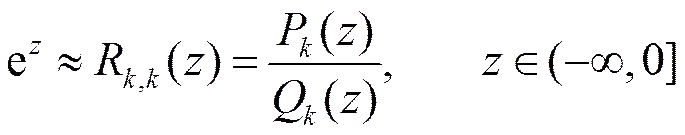
考虑到数值计算的稳定性,通常将式(4)写为以极点和留数表示的PFD (Partial Fraction Decomposition)形式如下:

式中:表示在‒∞处的极限值;α表示留数;θ表示极点;表示展开阶数。
由于极点通常是以共轭对的形式出现,因此可以利用此性质,将式(5)写成如下形式,其计算量节省为原来的一半。

PFD系数(、α和θ)可以在文献[11]提供的多项式系数的基础上通过Carathéodory-Fejér方法计算得到。根据文献[13]的研究,当阶数≤16时,Carathéodory-Fejér方法可保持较高的计算精度。本文选取=16,计算得到PFD系数如表1所示。

表1 16阶切比雪夫有理逼近方法的系数

当系数矩阵的元素是按照核素质量数增加的顺序排列时,矩阵具有稀疏结构,其求逆计算变得相对容易。
2 测试例题的计算结果
2.1O活化例题的计算结果
O活化例题如下:
O (stable)→(n,γ: 6.601 89×10b) →
O (stable)→(n,γ: 1.184 99×10b) →
O (stable)→(n,γ: 5.426 13×10b) →
O (β, 1.577 88×10s)
其中:相关的反应类型和截面已经在括号中予以标注;O的初始数量为10个;中子通量密度为10cm·s;中子辐照时间为1 a。
O活化例题的计算结果如表2所示。表2中,相对偏差定义为:(解析解‒CRAM计算结果)/解析解。其中解析解采用TTA计算得到,为追求较高的计算精度,截断标准设置为10。

表216O活化例题计算结果
在计算时,CRAM的时间步长直接取为1 a,所消耗的计算时间为0.0125 s,解析方法所消耗的计算时间为0.69 s,对于这种简单线性链来说,CRAM的计算效率高于解析方法。结合表2可以看到,采用CRAM进行中子辐照下的核素活化计算能够取得不错的效果,其计算精度和效率都比较高。
2.2 天然Fe活化例题的计算结果
天然Fe的初始质量为1 kg,富集度分布如下:Fe 5.8%、Fe 91.72%、Fe 2.2%、Fe 0.28%。相关的反应类型、截面和半衰期取自EAF-2007数据库。中子通量密度为3.641×10cm∙s,中子辐照时间为1 a。天然Fe活化例题中除了活化反应外,还有大量的衰变反应,因此本例题为活化衰变复合计算例题,计算结果如表3所示。
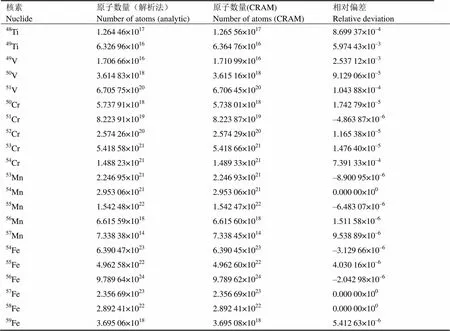
表3 天然Fe活化例题计算结果
在计算时,CRAM的时间步长直接取为1 a,所消耗的计算时间为2.37 s,解析方法所消耗的计算时间为11.84 s,对于这种复杂网状链来说,CRAM的计算效率高于解析方法。结合表3可以看到,采用CRAM进行中子辐照下的核素活化衰变计算能够取得不错的效果,其计算精度和效率都比较高。
2.3Fe衰变例题的计算结果
Fe衰变例题如下:
Fe (, 1.548×10s)→Fe (, 5.106×10s)→
Mn (, 1.166 8×10s)→Cr (stable)
其中:相关的反应类型和半衰期()已经在括号中予以标注;Fe的初始数量为10个。Fe衰变例题的计算结果如表4所示。
在计算时,CRAM的时间步长直接取为衰变时间。从表4可以看到,当衰变时间在10−10s时,CRAM的计算结果与解析解符合较好。但是当衰变时间大于10s,CRAM的计算结果严重偏离解析解。说明采用CRAM进行核素长期衰变计算可能导致计算错误。

表453mFe衰变例题计算结果

衰变时间Decay times53Fe原子数量(解析法)Number of 53Fe atoms (analytic)53Fe原子数量(CRAM)Number of 53Fe atoms (CRAM)相对偏差Relative deviation 1.0×1014.34912×10184.34912×10180.00000×100 1.0×1023.35819×10193.35819×10190.00000×100 1.0×1033.52942×10193.52943×10192.83333×10‒6 1.0×1041.82500×1014‒8.08213×1013‒1.44286×100 1.0×1050.00000×100‒8.49758×1012∞ 1.0×1060.00000×100‒1.42934×1011∞ 1.0×1070.00000×100‒8.16992×109∞ 1.0×1080.00000×100‒7.56749×108∞

衰变时间Decay times53Cr原子数量(解析法)Number of 53Cr atoms (analytic)53Cr原子数量(CRAM)Number of 53Cr atoms (CRAM)相对偏差Relative deviation 1.0×1015.93138×1025.93138×1020.00000×100 1.0×1025.21854×1055.21854×1050.00000×100 1.0×1031.84709×1081.84709×1080.00000×100 1.0×1045.37031×1095.37031×1090.00000×100 1.0×1055.88355×10105.88356×10101.69965×10‒6 1.0×1065.93488×10115.93488×10110.00000×100 1.0×1075.94001×10125.94001×10120.00000×100 1.0×1085.94052×10135.94052×10130.00000×100
3 收缩乘方技术的基本原理及应用效果
如前所述,式(3)中矩阵的特征值分布在复数平面的负实轴附近时,CRAM是矩阵指数在(‒∞, 0]区间的最佳有理逼近。对于核素衰变工况,矩阵的特征值会随着衰变时间而变大,即特征值的虚部也会相应变大,使得特征值显著偏离复数平面的负实轴。此时,如图1所示(详见文献[13]),采用CRAM近似矩阵指数,其计算精度会显著下降,甚至出现计算错误。这问题可以通过引入收缩乘方技术(Scaling and squaring)予以解决。

图1 16阶切比雪夫有理逼近方法(R16,16(At))近似矩阵指数的计算精度随矩阵At特征值的变化
3.1 收缩乘方技术的基本原理

收缩乘方技术就是通过选择合适的参数,使得能够被CRAM准确而高效地计算,随后通过对做次乘方运算,得到待求的矩阵指数。
采用收缩乘方技术后,式(3)可写成如下形式:

收缩乘方技术的本质是将总的计算时间划分为个时间步长。相对于矩阵,矩阵/特征值减小了倍,相应地其虚部也减小了倍,意味着特征值更靠近复数平面的负实轴,使得CRAM的适用性得到了更好的满足。
在选择参数时,一个常用的标准是取最小的,使得||||/≤1,其中||||是矩阵的谱范数,即||||=[(A)]。在Fe衰变例题中,矩阵的谱范数||||=0.00641,在谱范数计算领域这是一个很大的值,意味着矩阵是强刚性的,这主要是矩阵中各个元素的变化速率差别过大造成的,比如Fe的衰变常数为4.478×10s,Mn的衰变常数为5.969×10s,两者相差了12个量级。所以当衰变时间较长时,||||会远大于1,此时需要应用收缩乘方技术,以满足||||/≤1。
3.2 收缩乘方技术的应用效果
采用收缩乘方技术后,Fe衰变例题的计算结果如表5所示。

表5 采用收缩乘方技术后53mFe衰变例题计算结果

衰变时间Decay times53Fe原子数量(解析法)Number of 53Fe atoms (analytic)53Fe原子数量(CRAM)Number of 53Fe atoms (CRAM)相对偏差Relative deviation 1.0×1014.34912×10184.34912×10180.00000×100 1.0×1023.35819×10193.35819×10190.00000×100 1.0×1033.52942×10193.52935×1019‒1.98333×10‒5 1.0×1041.82500×10141.82490×1014‒5.47945×10‒5 1.0×1050.00000×1000.00000×1000.00000×100 1.0×1060.00000×1000.00000×1000.00000×100 1.0×1070.00000×1000.00000×1000.00000×100 1.0×1080.00000×1000.00000×1000.00000×100
(续表5)

衰变时间Decay times53Mn原子数量(解析法)Number of 53Mn atoms (analytic)53Mn原子数量(CRAM)Number of 53Mn atoms (CRAM)相对偏差Relative deviation 1.0×1012.98086×10162.98086×10160.00000×100 1.0×1022.51294×10182.51294×10180.00000×100 1.0×1036.35698×10196.35687×1019‒1.73038×10‒5 1.0×1049.99998×10199.99990×1019‒8.00002×10‒6 1.0×1051.00000×10209.99998×1019‒2.00000×10‒6 1.0×1061.00000×10209.99998×1019‒2.00000×10‒6 1.0×1071.00000×10209.99998×1019‒2.00000×10‒6 1.0×1089.99999×10199.99998×1019‒1.00000×10‒6

衰变时间Decay times53Cr原子数量(解析法)Number of 53Cr atoms (analytic)53Cr原子数量(CRAM)Number of 53Cr atoms (CRAM)相对偏差Relative deviation 1.0×1015.93138×1025.93138×1020.00000×100 1.0×1025.21854×1055.21854×1050.00000×100 1.0×1031.84709×1081.84706×108‒1.62418×10‒5 1.0×1045.37031×1095.37028×109‒5.58627×10‒6 1.0×1055.88355×10105.88356×10101.69965×10‒6 1.0×1065.93488×10115.93488×10110.00000×100 1.0×1075.94001×10125.94001×10120.00000×100 1.0×1085.94052×10135.94052×10130.00000×100
鉴于矩阵的谱范数||||=0.00641,为了满足标准||||/≤1,时间步长/被选为100 s。这样对于衰变时间为10s的情况,就需要划分为10个时间步长进行计算,可预计的时间消耗是很大的。但是由表5可以发现,对于像Fe、Fe这样的短寿命核素,在衰变10s时,原子数量已经减少到0个,此时可以从矩阵中将它们移除,相应地新的矩阵的谱范数变为5.940 58×10,在||||/≤1条件下,时间步长可以取到10s,使得计算效率得以大幅提高。经统计,对于衰变时间为10s的情况,解析方法的计算耗时为0.53 s,耦合了收缩乘方技术的CRAM的计算耗时为0.62 s,两者基本相当。
此外,从表5可以看到,耦合了收缩乘方技术后,采用CRAM进行核素长期衰变计算就可以得到准确的结果。
4 结语
本文介绍了CRAM的基本理论,以及应用于求解核素平衡方程的实现方式。选取O核素和天然Fe元素活化例题以及Fe核素衰变例题对CRAM进行了测试验证,并与TTA方法得到的解析解进行了对比。
对于存在中子反应的问题来说,TTA方法在将闭环反应链线性化过程中,会截断和舍弃一部分反应链,因此从原理上来说会有一定误差,但是如果截断标准选取得比较严格,闭环反应链线性化引入的误差是很小的,但是会增加大量的计算时间。而CRAM方法不会对闭环反应链进行截断和舍弃,因此不存在这方面的误差,其计算精度比较高,而且可以采用大的计算步长,因此计算效率也比较高。
对于核素衰变问题,不涉及闭环反应链,因此TTA方法可以直接给出精确的解析解,计算效率也比较高。CRAM方法对于核素短期衰变计算是适用的,时间步长可以直接取为衰变时间,但是对于核素长期衰变计算,如果时间步长直接取为衰变时间,矩阵的特征值会偏离复数平面的负实轴,此时采用CRAM方法计算容易出现计算错误。因此需要配合使用收缩乘方技术,使得CRAM方法的适用性得到更好的满足,收缩乘方技术的应用会一定程度上降低CRAM方法的计算效率,但是仍然与TTA方法相当。
后续将对CRAM方法进行进一步的测试验证和工程应用。
1 李璐, 张竞宇, 郭庆洋, 等. 水冷聚变堆主回路活化产物源项计算分析[J]. 核技术, 2016, 39(11): 110603. DOI: 10.11889/j.0253-3219.2016.hjs.39.110603. LI Lu, ZHANG Jingyu, GUO Qingyang,. Calculation and analysis of activation products source term in water-cooled fusion reactor primary circuit[J]. Nuclear Techniques, 2016, 39(11): 110603. DOI: 10.11889/j.0253-3219.2016.hjs.39.110603.
2 石巍, 曾勤, 李卫, 等. CFETR第一壁及赤道面外包层中子辐照损伤初步分析[J]. 核技术, 2016, 39(12): 120602. DOI: 10.11889/j.0253-3219.2016.hjs.39.120602. SHI Wei, ZENG Qin, LI Wei,. Primary analysis of radiation damage on first wall and the outboard blanket on equatorial plane for CFETR[J]. Nuclear Techniques, 2016, 39(12): 120602. DOI: 10.11889/j.0253-3219.2016.hjs.39. 120602.
3 Lyu X W, Xia X B, Zhang Z H,. Analysis of tritium production in a 2 MW liquid-fueled molten salt experimental reactor and its environmental impact[J]. Nuclear Science and Techniques, 2016, 27(4): 78. DOI: 10.1007/s41365-016-0100-z.
4 Cetnar J. General solution of bateman equations for nuclear transmutations[J]. Annals of Nuclear Energy, 2006, 33(7): 640‒645. DOI: 10.1016/j.anucene.2006.02. 004.
5 吴明宇, 王事喜, 杨勇, 等. 回溯算法在燃耗计算中的应用[J]. 原子能科学技术, 2013, 47(7): 1127‒1132. DOI: 10.7538/yzk.2013.47.07.1127. WU Mingyu, WANG Shixi, YANG Yong,. Application of backtracking algorithm to depletion calculations[J]. Atomic Energy Science and Technology, 2013, 47(7): 1127‒1132. DOI: 10.7538/yzk.2013.47.07. 1127.
6 Croff G. Origen2: a versatile computer code for calculating the nuclide compositions and characteristics of nuclear materials[J]. Nuclear Technology, 1983, 62: 335‒352. DOI: 10.13182/NT83-1.
7 Leppänen J, Pusa M, Viitanen T. The serpent Monte Carlo code: status, development and applications in 2013[J]. Annals of Nuclear Energy, 2015, 82: 142‒150. DOI: 10.1016/j.anucene.2014.08.024.
8 She D, Wang K, Yu G L. Development of the point-depletion code DEPTH[J]. Nuclear Engineering and Design, 2013, 258(17): 235‒240. DOI: 10.1016/ j.nucengdes.2013.01.007.
9 Pusa M, Leppanen J. Computing the matrix exponential in burnup calculations[J]. Nuclear Science and Engineering, 2010, 164(2): 140‒150. DOI: 10.13182/NSE09-14.
10 Cody W J, Meinardus G, Varga R S. Chebyshev rational approximation to exp(‒) in [0, +∞] and applications to heat conduction problems[J]. Journal of Approximation Theory, 1969, 2(1): 50‒65. DOI: 10.1016/0021-9045 (69)90030-6.
11 Carpenter A J, Ruttan A, Varga R S. Extended numerical computations on the “1/9” conjecture in rational approximation theory[J]. Lecture Notes in Mathematics, 1984, 1105(4): 383‒411. DOI: 10.1007/BFb0072427.
12 Trefethen L N, Weideman J A C, Schmelzer T. Talbot quadratures and rational approximations[J]. BIT Numerical Mathematics, 2006, 46(3): 653‒670. DOI: 10.1007/s10543-006-0077-9.
13 Pusa M. Higher-order Chebyshev rational approximation method and application to burnup equations[J]. Nuclear Science and Engineering, 2016, 182(3): 297‒318. DOI: 10.13182/NSE15-26.
14 Moler C, Loan C V.Nineteen dubious ways to compute the exponential of a matrix[J]. SIAM Review,1978,20(4): 801‒836. DOI: 10.1137/1020098.
Application of Chebyshev rational approximation method in inventory calculation of radioactive nuclides
ZHANG JingyuMA YadongCHEN YixueGAO Qiang
1(School of Nuclear Science and Engineering, North China Electric Power University, Beijing 102206, China) 2(Nuclear and Radiation Safety Centre, Ministry of Environmental Protection, Beijing 100082, China)
Background: The material suffering from strong neutron irradiation in the nuclear reactor will be activated to be radioactive nuclides. These nuclides and their decay products contribute a significant part to the occupational radiation exposure (ORE) of personnel. Purpose: For better radiation protection of the workers in nuclear reactor, it is supposed to calculate the inventory of radioactive nuclides accurately. Methods: Compared with other methods for solving the equilibrium equations of nuclides, the Chebyshev rational approximation method (CRAM) has comprehensive advantages on computational accuracy and efficiency. In this paper, the theory of CRAM method is described firstly, and then some typical cases are tested to verify CRAM method. Results & Conclusion: Compared with the analytical solution, CRAM method shows good effect on activation and decay calculation of nuclides under neutron irradiation, but may cause obvious error on long-term decay calculation of nuclides. After coupling with technique of scaling and squaring, CRAM method can derive accurate results for long-term decay calculation of nuclides and its scope of application is extended.
CRAM, Radioactive nuclides, Inventory calculation, Scaling and squaring
TL99
10.11889/j.0253-3219.2017.hjs.40.080502
国家自然科学基金(No.11605058)、国际热核聚变实验堆计划专项(No.2014GB119000)、中央高校基本科研业务费专项资金(No.2017MS041)资助
张竞宇,男,1984年出生,2013年于清华大学获博士学位,研究领域为核反应堆燃料燃耗/材料活化计算
高强,E-mail: gaoqiang@chinansc.cn
2017-01-20,
2017-03-24
National Natural Science Foundation of China (No.11605058), National Special Project for Magnetic Confined Nuclear Fusion Energy (No.2014GB119000),the Fundamental Research Funds for the Central Universities(No.2017MS041)
ZHANG Jingyu, male, born in 1984, graduated from Tsinghua University with a doctoral degree in 2013, focusing on the calculation of fuel depletion/material activation
GAO Qiang, E-mail: gaoqiang@chinansc.cn
2017-01-20, accepted date: 2017-03-24

