纯电动汽车充电桩的数量优化

朱成军Zhu Chengjun



纯电动汽车充电桩的数量优化

朱成军Zhu Chengjun

（武汉理工大学 现代汽车零部件技术湖北省重点实验室，湖北武汉 430070）

充电基础设施对纯电动汽车的发展有直接影响，优化充电桩数量有利于基础设施建设。利用随机离散事件建立排队模型，仿真深圳某充电站内排队指标。结果表明充电桩最优数量低于当前数量，通过优化配置可以降低充电服务成本，为企业规划与基础设施建设提供参考。

充电桩；充电排队；优化配置

1 纯电动汽车的运行特性

近年来，深圳示范运行大量纯电动出租车，取得了良好的社会与经济效益[1]。随着快速充电技术日渐完善，国家相关部门确定整车快速充电技术路线的原则[2]。在整车快速充电模式中，充电桩数量的多少影响充电站的建设和充电用户的使用体验。对充电过程建立排队模型，根据排队模型的指标可以对充电桩数量进行优化。

1.1 充电数据统计分析

采集充电站2016年11月份连续10天的充电数据进行分析，利用Matlab统计工具箱近似判断统计数据的分布规律[3]。充电开始间隔时间的统计如图1所示，充电时长的统计如图2所示。

由图1、图2可以近似判断充电开始间隔时间服从负指数分布，充电时长服从正态分布。为得到正确的判断，对充电数据进行分布检验。

1.2 充电数据分布检验

采用Matlab统计工具箱kstest函数对数据进行负指数分布的K-S检验[4]。当0=0时认为充电间隔时间服从负指数分布，当0=1时认为不服从负指数分布。显著性水平取为0.05，统计数据结果见表1。

利用lillietest函数对充电时长进行检验，结果见表2，认为显著性水平为0.05，充电时长服从正态分布。

经过检验，电动出租车的充电时长服从正态分布，充电开始间隔时间服从负指数分布。

表1 充电间隔时间负指数分布检验结果

组别样本数量充电间隔均值/minh0值 14012.110 24013.810 33713.560 44910.760 54312.130 64412.870

表2 充电时长正态分布检验结果

组别样本数量充电时长均值/min标准差h0值 14064.5321.550 24056.8821.940 33763.6821.620 44960.5222.110 54359.4524.120 64463.7922.810

2 纯电动汽车充电排队模型

根据充电站运营经验，充电过程为多服务台排队系统，如图3所示。

排队系统建模仿真的目标是探索纯电动汽车与充电桩之间的充电时间关系，确保系统具备最优的服务效率和充电桩数量，利用排队系统建模求解充电桩数量优化配置问题[5]。

2.1 混合制充电排队模型

通过对纯电动出租车运行特性的分析，建立充电排队系统的混合制////∞/FIFO模型[6]。其中为开始充电间隔服从负指数分布；为充电时长服从正态分布；为充电桩的数量；为充电站最多可以停靠的车辆数，包括正在充电和排队的车辆；∞为充电车辆来源是无限的；FIFO为先到先服务的排队规则。

纯电动汽车充电是离散事件系统，可以由Matlab/SimEvents模块集中进行建模[7]。根据充电服务流程，设定输出端口，仿真框图如图4所示。

2.2 排队系统模型变量说明

根据排队论基本理论[8]，系统达到平稳状态后，当整个充电站系统状态为时，充电概率为p={=}，其中为整个充电站内的车辆数。

为车辆到达率分布，即单位时间内到达充电站的车辆数量情况，则1/为车辆到达充电站的平均间隔时间；为充电服务时间分布，即单位时间内完成充电的车辆数量，则1/为平均完成充电时间。

单台充电桩的服务强度为，指平均充电时间与平均到达间隔的商，即=(1/)/(1/)=/。对于有台充电桩的充电站，其服务强度为s=/=/()，在s<1时，充电站才能正常运转；即车辆到达率小于服务率，队列才能达到平衡状态。

定义s为充电桩在单位时间内的服务费用，包含电费、设备损耗费和维护费用等；w为车辆单位时间内损失的费用，主要指由于排队时间而导致的损失；（）为充电桩及车辆总损失的目标函数，′为（）最小时的充电桩数量。

对于充电桩数量为，系统容量限制在以下的排队系统，充电站内所有充电桩都处于空闲状态的概率0为

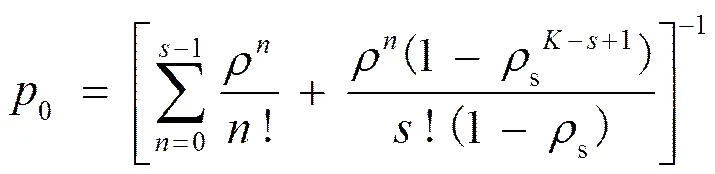
考虑充电站面积限制，当充电站内车辆总数达到时，后续车辆会选择离开。此时的排队情况是损失制排队，损失的概率为k

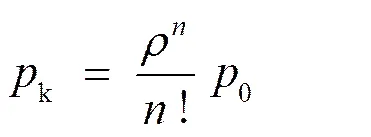
综合车辆损失情况后的车辆有效到达率为e

e=(1-k) （3）

2.3 排队系统主模型

排队系统的主模型是以各种指标来表示排队系统的状态。

排队等待的车辆数（不包括正在充电车辆数）为平均队长，用q表示

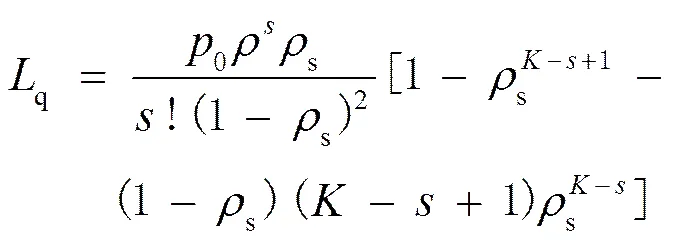
充电站内接受充电车辆和排队等待车辆总数为平均车辆数，用s表示

（5）

车辆在排队等待时间的均值为平均排队时间，用q表示

车辆在充电站内停留的总时间为平均停留时间，用s表示

（7）

以单位时间内充电桩服务费用与车辆等待费用之和（）为目标，得到充电桩的最优化配置函数为

可以求得（）最小时的充电桩最优数量′值，由于′为整数，所以得到最优化′的求解函数为

（9）

根据s和w的比值与s之间的关系，可以确定充电桩的最优数量。由以上主模型的各个指标，可以对充电桩数量进行合理化配置。

3 充电桩数量优化分析实例

3.1 充电排队系统模型指标

对纯电动出租车充电时间进行分段，交接班（早6：00、晚18：00）前的充电时间为一类充电时段，饭间或休息时段（非交接班时间范围）的充电为二类时段。基于对充电站实际运营数据的统计分析，得到充电车辆到充电站的时间间隔为负指数分布。对于一类时段，平均到达间隔时间为1/1= 11.25 min，平均充电时间为1/1=60.15 min；对于二类时段，平均到达间隔时间为1/2=14.19 min，平均充电时间为1/2=56.48 min。

当前充电站内充电桩的数量为10个，根据运营经验可以确定=12辆。根据s<1，可以得到一类时段最小充电桩的数量为=5。

进行仿真分析，得到不同充电桩数量对应的充电排队服务系统的运行指标，见表3。

表3 一类时段充电服务系统运行指标

s/个Lq/辆Ls/辆Wq/minWs/minρs 53.538.8843.68109.760.99 62.097.4327.9799.670.89 71.266.6118.0194.370.76 80.796.1411.7491.180.67 90.505.85 7.6188.830.59 100.145.48 2.1385.770.49

从表3中可以看出，随着充电桩数量增加，排队系统的队长呈不断减小趋势，但不成比例关系。对于二类充电时段，计算其最小充电桩数量为=4。不同充电桩数量对应的二类充电时段充电服务系统运行指标见表4。

表4 二类时段充电服务系统运行指标

s/个Lq/辆Ls/辆Wq/minWs/minρs 43.587.5656.64119.570.99 51.815.7931.63101.050.79 61.014.9918.55 92.010.66 70.624.6011.65 86.810.57 80.414.39 7.67 83.160.51 90.274.25 5.13 80.290.45

从表3、表4可以判断，在一类时段，充电桩合理个数为7、8和9；在二类时段，充电桩的合理个数为6和7。

3.2 充电桩及车辆的损失费用

每个充电桩单位时间的服务费用s为

式中，根据深圳某公司的数据，DF=2 404.26元，为充电站平均一天的充电电费；SB=30 000元，为单个充电桩设备费用；TJ=90 000元，为单个充电桩平均土木建设费用；WH=3 000元，为单个充电桩维护费用；=10个，为充电站充电桩数量；=8年，为充电桩使用年限。据此，可以计算出s=11.76元/h。

驾驶员的平均月收入按7 000元计算，每月按30天计算，每天工作时间为12 h，可以计算出w=19.44元/h。

3.3 充电桩数量的配置

由以上计算实例可以计算出在混合制排队模型下，该充电站在一类时段的最优充电桩配置数量为8个，在二类时段的最优充电桩配置数量为6个，均低于当前充电站内配置数量10个。

在一类时段与实际情况较符合，但并不是最优的配置数量，从而验证所建模型的准确性与有效性。在二类时段，充电桩最优化配置数量为6个，在这个时段内充电桩的闲置时间比较长。但从市场发展规律以及企业规划来考虑，企业在当前配置的充电桩数量较为合理，企业适当地多配置充电桩有利于企业未来发展。

4 结 论

通过采集充电站实际数据，分析充电车辆的运行特性，根据其特点建立了反映真实情况的混合制排队模型。

根据实际运营数据对混合制排队模型进行实例仿真计算，得出不同时段下排队模型的运行指标。以整个充电站服务系统总费用最低为目标函数，得出充电站内充电桩的最优配置数量，仿真计算结果检验了模型的正确性和有效性。根据优化得出的充电桩数量，结合市场及企业发展情况，可以为充电运营企业的充电站建设和规划提供参考。

[1]朱蓉文，劳铖强. 深圳新能源汽车产业发展现状与对策[J]. 特区实践与理论，2015（2）：97-100.

[2]中国电工技术学会电动车辆专业委员会. 我国电动汽车市场化进程中相关问题综述[J]. 电工电能新技术，2015，34（7）：1-10.

[3]谢中华. Matlab统计分析与应用：40个案例分析[M]. 北京：北京航空航天大学出版社，2010：163-178.

[4]张维戈，陈连福，黄彧，等. M/G/k排队模型在电动出租汽车充电站排队系统中的应用[J]. 电网技术，2015，39（3）：724-729.

[5]王维平. 离散事件系统建模与仿真（第二版）[M]. 北京：科学出版社，2007：42-51.

[6]何选森. 随机过程与排队论[M]. 长沙：湖南大学出版社，2010: 96-122.

[7]薛定宇，陈阳泉. 基于Matlab/Simulink的系统仿真技术与应用.第2版[M]. 北京：清华大学出版社，2011：359-366.

[8]Kimura T. Diffusion Approximation for an M/G/m Queue[J]. Operations Research, 1983, 31(2): 304-321.

2017-03-17

1002-4581（2017）04-0004-04

U469.72

A

10.14175/j.issn.1002-4581.2017.04.002