深刻理解教材践行“用教材教”——“平方根（第一课时）”教学实录与反思

■刘瑞祥

深刻理解教材践行“用教材教”
——“平方根（第一课时）”教学实录与反思

■刘瑞祥

一、教材分析

“平方根”共2个课时，本节课是第一课时。由于实际计算中需要引入无理数，使数的范围从有理数扩充到了实数，从而完成了初中阶段对数的扩展。运算方面，在乘方运算的基础上引入了开方运算，使代数运算得以完善。因此，本节课有助于了解n次方根的概念，为今后学习二次根式、方程、函数等做了铺垫。

二、教学目标

了解平方根的概念，学会平方根的符号表示；了解开方与乘方互为逆运算，会用平方根运算求一个非负数的平方根；理解平方根的性质，懂得一个正数有两个平方根（它们互为相反数），0的平方根是0，负数没有平方根。

三、教学重点

了解开方与乘方互为逆运算，能熟练地用平方根运算求一个非负数的平方根。

四、教学难点

用平方根运算求一个非负数的平方根。

五、教学过程

1.创设情景，复习旧知。

师：想一想，什么是乘方运算？能举个例子说说吗？

生1：32，（-3）2，52，54……

师：在“54”中，5、4分别叫什么？

生（众）：5是底数，4是指数。

师：54的结果是多少？它又叫什么？

生（众）：625，幂。

师：很好，乘方运算就是已知底数、指数，求幂的运算。

2.提出问题，引发探究。

师：如果知道了指数、幂，底数是多少呢？也就是说“已知x4=625，求x”。我们把这种运算称之为开方运算，就是已知幂、指数，求底数的运算。

师：我们研究数的运算往往是从简单的开始，你们觉得我们可以先从“开几次方”开始研究呢？

生2：开1次方。

师：对于一个数的开1次方，是多少？有没有必要？

生3：没有必要，开1次方还是它本身。

师：对的！那从开几次方开始？

生4：开2次方。

师：到底开几次方？

生（众）：开2次方。

师：2次方又称平方。那我们就从平方运算和对应的开平方运算开始。我们知道，22=4，若x2=4，x是多少？

生5：±2。

师：若x2=100呢？或者x2=169呢？

生6：±10、±13。

师：能再举些例子吗？

生7举例。

师：你们有什么发现？

生8：平方等于同一个数的数有两个，它们互为相反数。

师：x2=2呢？（学生讨论。）

师：在这里我们没有找到任何一个整数或分数的平方等于2，即无法找到一个有理数，使它的平方等于2。这怎么办呢？

师：为了确定一个数，使它的平方等于2，我们在平方数2的上面放上符号“”来表示，记

师：可以看出，使x2＝a（a＞0）成立的数有几个呢？

生（众）：两个。

师：它们之间有什么关系？

生10：它们互为相反数。

教师接着给出平方根的定义，并板书。

3.尝试练习，巩固新知。

教师出示例题，让学生讲解，然后教师点评，巩固新知。

例1求下列各数的平方根：

4.探索交流，发现性质。

师：在下列各括号中能填写适当的数使等式成立吗？如果能，请填写；如果不能，请说明理由，并与同学交流。

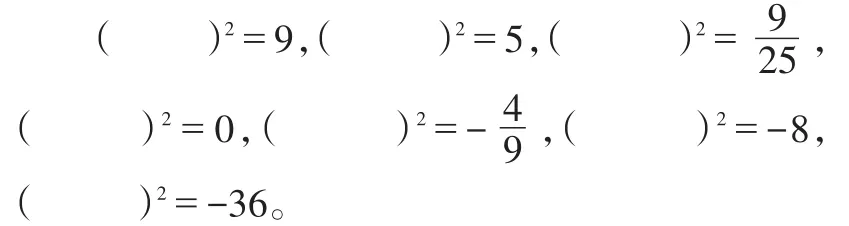
生11进行了回答。

师：你有什么发现？

生12、生13、生14给出了自己的见解。教师接着板书平方根的性质：一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根。

5.拓展练习，深化理解。

教师出示例题。

例2计算：

生15：表示36的平方根。

师：再想想，看看黑板上的符号表示。生16：表示36的正的平方根。

师：正确！等于多少呢？

生17：6。

师：等于多少？

生20：表示0.81的平方根。

师生共同分析后，学生上台板演。

6.梳理小结，归纳提升。

师：请同学们围绕以下几个问题展开梳理：（1）这节课你是怎样学习平方根的？（2）你对平方根有哪些认识？

生21回答。

师：同学们，乘方运算是已知底数、指数求幂的运算，开方运算是已知幂、指数求底数的运算，如果已知幂、底数，求指数叫什么运算呢？你们将在高中的学习中继续探究。

六、教学反思

1.立足研究教材，贴近学生现实。

著名特级教师李庾南认为，“教材不等于教学内容，教者应该从学生实际出发，力求学生的知识、智力、能力、情感、态度能达到各自的‘最近发展区’，创造性地用教材，重组教学内容，决不能只是讲教材”。本节课的教材设计是以运用勾股定理计算直角三角形边长为实际情境，引导学生感悟研究“数的开方”的必要性，激发学生的求知欲。显然，边长的计算结果应该是算术平方根，而不是平方根，笔者觉得有值得商榷的地方。所以，笔者放弃了教材上的情境引入，而是从“什么是乘方运算”入手，引入“开方运算”，让学生初步感受乘方与开方互为逆运算，然后引导学生具体研究平方运算和对应的开平方运算，再给出平方根的定义，让学生学会平方根的符号表示及求法，并归纳其性质。这样，不仅有利于学生理解平方根的内涵，还能够更好地揭示开平方运算与平方运算之间的内在关联。

2.深刻理解教材，认真理解数学。

钟启泉教授指出：“唯有‘用教材教’才能反映教学过程中教材的性质。这是因为，教学过程是一种社会交互作用的过程，知识不是教师通过传递信息强制性地灌输给学生的，而是学生自身以及在与教师交互作用之中建构的。”章建跃教授曾说：“在课堂教学中，要以数学知识的发生、发展过程和理解数学知识的心理过程为基本线索，为学生构建前后一致逻辑连贯的学习过程，使他们在掌握数学知识的过程中学会思考。”“用教材教”就需要我们深刻理解教材、认真理解数学，不仅包括本学段内数学知识的发生、发展可能，还要思考在后续高中阶段会有怎样的生长可能，也有利于学生能从整体上理解数学，构建数学认知结构。“幂、底数、指数”三个量之间的关系是平方根教学的生长点，笔者设计具有思考性的问题串，引发学生思维冲突，引导学生准确而深刻理解平方根概念，也为学生学习高中的对数知识做了必要的准备。