大地电导率对GMD感应地电场的影响规律研究

刘青，徐婷，韩康康，戎娅婕

（1.西安科技大学，陕西西安 710054；2.新疆电力设计院，新疆乌鲁木齐 830001）

大地电导率对GMD感应地电场的影响规律研究

刘青1，徐婷1，韩康康1，戎娅婕2

（1.西安科技大学，陕西西安 710054；2.新疆电力设计院，新疆乌鲁木齐 830001）

鉴于深层大地电导率参数难以获得，研究GMD感应地电场对大地电导率的敏感性对GIC评估及防护更具指导意义。基于平面波法，研究了不同大地模型对感应地电场的影响规律。结果表明高阻地区出现的感应地电场幅值更大，不同地区东西向与南北向感应地电场大小关系不仅与纬度有关，同时与大地模型特点有关；对于多层大地电导率模型，感应地电场幅值对顶层电导率更敏感，且随着底层电导率的减小，影响规律越明显。

地磁扰动；感应地电场；大地电导率；磁暴；地磁感应电流

太阳活动引起的地磁扰动（geomagnetic disturbance，GMD）会在大地、海洋等导电介质中诱发感应地电场，从而在电网、油气管网等与大地构成回路的人工导体系统中产生准直流性质的地磁感应电流（geomagnetically induced currents，GIC）[1-3]，威胁电网、油气管网的安全运行[4]。北美、北欧等高纬度地区，由于地磁场变化剧烈，曾多次出现GIC损坏变压器、甚至导致大规模停电事故[5-6]。近年来，我国及南非、日本等中低纬度国家也出现GIC侵害电网事故[7-9]，例如2004年11月10日发生的强磁暴中，岭澳核电站监测到幅值高达75.5 A的GIC[10]。我国电网、油气管网规模庞大，并且正以空前的速度发展，GIC的致灾风险将进一步增加，有必要全面评估电网及油气管网的GIC水平。GMD感应地电场是技术系统中GIC的“源”，因此评估GIC的前提是探明磁暴期间的感应地电场及受大地电性结构的影响规律。

磁暴发生时电离层电流体系复杂，因此建立场源模型和大地模型时需要合理简化。对于场源电流体系，常采用位于空中一定高度的水平面电流源或无限长线电流源[11-13]简化模型；对于大地，一般采用电导率随深度变化的一维水平分层结构。考虑到“场—源”距离很大，可以结合地面地磁台站的监测数据采用平面波方法求解感应地电场[14-16]。由于GMD频率极低（0.01～0.000 1 Hz），对于一般的大地电导率参数，电磁波的趋肤深度高达几百甚至上千公里。运用平面波法计算GMD感应地电场需结合深层大地电导率参数，而由于大地探测工作量及技术的局限，获得精确的深层大地电导率参数是很困难的，因此，研究大地电导率及分层厚度等因素对感应地电场的影响规律对GIC风险评估更有意义。本文利用2006年12月14日至15日的磁暴监测数据，采用平面波法计算感应地电场，获得感应地电场对大地电导率参数等不确定性因素的敏感性规律，影响规律可为电网、油气管网的GIC风险评估提供一定的指导。

1 求解磁暴感应地电场的基本方程

磁暴时地面观测到的地磁变化主要是位于地面上方100 km左右的电离层电流变化引起，根据平面波的假设，电磁波垂直入射大地。建立直角坐标系，规定z轴垂直向下，z=0的平面为地平面；x轴指向地理北极，y轴指向正东。

对于电导率水平分层大地，根据maxwell方程和faraday电磁感应定律可得，在第m层中电场x轴分量及磁场y轴分量可分别表示为

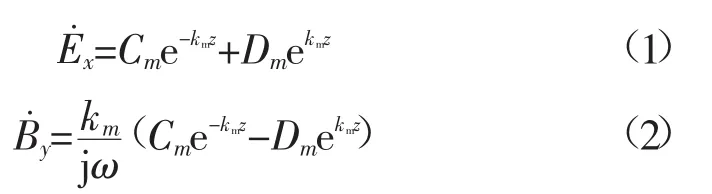
式中：μ0为真空磁导率；σm为第m层大地电导率；Cm，Dm为第m层积分常数。

对于最底层（第n层），厚度趋于无穷大，积分常数为0，则波阻抗为

由于其各层（m＜n）厚度都是有限的，不存在无穷边界条件，积分常数Cm，Dm都不为0。因此，第m层的波阻抗为

将反射系数用第m层底面的波阻抗来表示

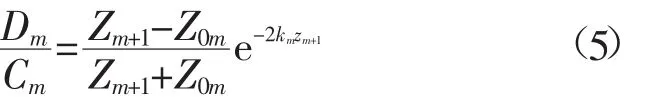
将式（5）代入式（4），得第m层顶面波阻抗为

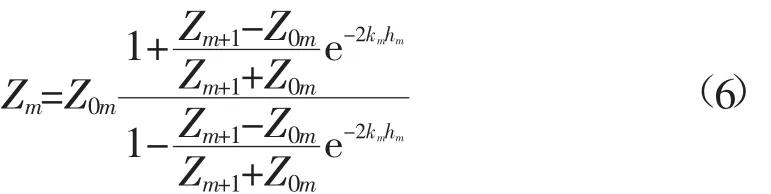
式中，hm为第m层的厚度。从底层出发，反复利用递推公式（6），可得到地面波阻抗Z0。

磁场的x、y分量可由地面的地磁监测台站获得，在已知大地电性结构的前提下，根据式（7）可计算得到感应地电场的y、x分量。

2 典型高阻及低阻大地对感应地电场的影响

大地电性结构及分布非常复杂，而对感应地电场建模主要考虑大地电导率的差异。本文在全球范围内收集整理了30多个典型大地电导率分层模型，并从中选取了4个典型代表，其中模型1、2作为高阻大地的典型代表，模型3、4作为低阻大地的典型代表。4种大地模型电阻率随深度变化如图1和图2所示。

图1 典型高阻大地电导率分布Fig.1 Typical high resistivity ground conductivity distribution

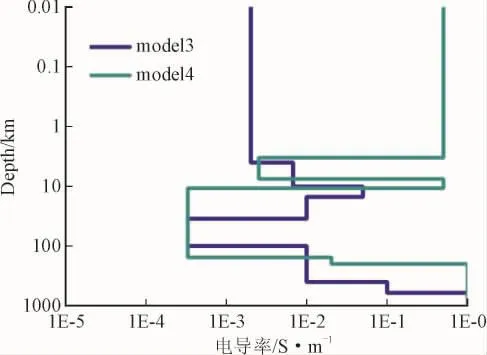
图2 典型低阻大地电导率分布Fig.2 Typical low resistivity ground conductivity distribution

根据4个典型大地模型的电导率参数计算其地表阻抗Z0，Z0的幅频和相频特性分别如图3和图4所示。

图3 4种大地模型地表阻抗的幅频特性Fig.3 Amplitude frequency characteristics of ground impedance for 4 geodetic models

图4 4种大地模型地表阻抗的相频特性Fig.4 Amplitude frequency characteristics of ground impedance for 4 geodetic models

从图中可看出，低频时地表阻抗的幅频、相频特性差异不大，而随着频率增加，高阻模型的地表阻抗幅值远大于低阻模型，高阻模型可能产生更大的感应地电场；高阻模型地表阻抗的相位变化大于低阻模型；随着频率的增大阻抗幅值增大，意味着GMD扰动频率越快，感应地电场越大。

选取2006年12月14日至15日的磁暴事件，利用3个不同纬度地磁台的监测数据，计算上述典型4种土壤模型下感应地电场，北向和东向电场峰值分别如图5、6所示。北京（40.3°N）、兰州（36.1°N）和肇庆（23°N）地磁台纬度由高至低分别相差4.2°及13.1°，可以看出在同一次磁暴事件中纬度越高感应地电场越大；大地电导率结构及参数对地电场影响很大，针对同一纬度地区，高阻模型感应地电场大于低阻模型感应地电场，如北京地磁监测数据下，高阻模型的感应地电场是低阻模型感应地电场的3～4倍；对于所选磁暴事件，由北京和兰州地磁监测数据计算出的模型3、4的感应地电场南北向大于东西向，而其余情况反之。由此说明在中低纬度地区东西向地电场并不一定大于南北向地电场，应结合磁暴纬度和大地模型具体分析。

图5 南北方向的感应地电场Fig.5 Induced geoelectric field in north-south direction

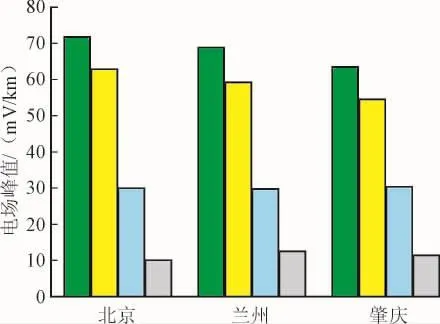
图6 东西方向的感应地电场Fig.6 Induced geoelectric field in east-west direction

3 感应地电场对大地电导率分布的敏感性分析

时谐电磁场在均匀大地导体内传播时的趋肤深度（km）可由式（8）求得

磁暴发生时地磁场变化频率范围为0.000 1～0.01 Hz，考虑大地电导率变化范围为0.000 1～0.1 S/m，由（8）可知电磁场的透射深度可达几百甚至数千千米。大地电磁测深数据表明，大地100 km以下土壤电导率大于0.01 S/m，以下我们将分别研究两层大地和多层大地电导率结构及参数对感应地电场的影响，分析中结合地磁场频率变化范围，上层厚度最大考虑到500 km。

3.1 双层大地模型

本节中假设大地为双层结构，基于不同地质类型的大地电导率取值，研究电导率对感应地电场的影响。计算中，分别选取上层或下层大地电导率为0.01 S/m，另一层大地电导率在[0.000 1，0.1]S/m范围内变化。上层厚度h1分别为1 km、10 km、100 km、300 km、500 km时，采用上述北京地磁台数据，以感应出的东西向电场为例分析电场峰值随电导率变化规律，如图7和图8所示。

图7 感应地电场随下层电导率变化曲线Fig.7 Conductivity curve of induced geoelectric field with lower layer

图8 感应地电场随上层电导率变化曲线Fig.8 Conductivity curve of induced geoelectric field with upper layer

结果表明感应地电场随大地电导率增大而减小；电场幅值变化程度与上层厚度有关，当下层电导率小于上层电导率时，感应地电场随上层厚度增大而减小，反之增大。上层电导率小且厚度大的大地电性结构感应出的电场更大。

为了更直观地反应电导率及上层大地厚度对感应电场的影响，将上述不同情况的电场幅值变化范围用图9描述。图中黑色、红色曲线分别表示底层电导率为0.000 1 S/m、0.01 S/m的情况。可见，当上层大地电导率在 [0.000 1，0.1]S/m范围内变化时，随着上层厚度h1的增加，电场幅值的变化范围变大，且底层电导率越小，上述规律越明显。

图10是上层厚度h1为500 km，上层大地电导率在0.000 1～0.1 S/m范围内变化，底层大地电导率在0.01～0.1 S/m范围内变化时感应地电场峰值的变化规律。可见，感应地电场随上层电导率增大而急剧减小；底层电导率变化对电场幅值影响很小，根据计算结果最大差别不超过7%，故500 km以下电导率由0.01～0.1 S/m内引起的感应地电场变化可以忽略，后续分析500 km以下大地电导率可直接取其最小值0.01 S/m考虑电场最大的情况。

图9 上层电导率引起的感应地电场变化范围Fig.9 The variation range of induced geoelectric field induced by upper conductivity

图10 底层及上层电导率变化下感应地电场Fig.10 Induction electric field under the change of conductivity at lower and upper layers

3.2 多层大地模型

本节中分析感应地电场对多层大地各层电导率的敏感性，首先考虑三层大地，取顶层及第二层厚度相同，即h1=h2=250 km，底层电导率取0.01 S/m，图11是顶层及第二层电导率对感应地电场幅值的影响，可以看出在顶层及第二层厚度相同时，电场受上层电导率变化敏感性较大。

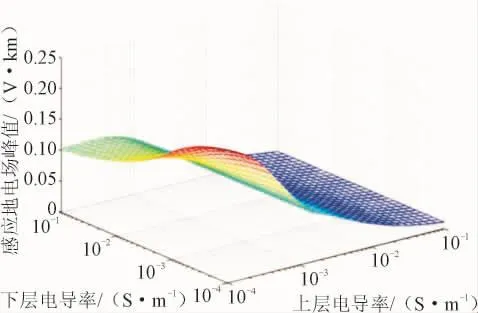
图11 顶层及第二层电导率变化感应地电场Fig.11 Induction electric field under the change of conductivity at top and second layers

为了分析感应地电场对每层大地电导率的敏感程度，以四层模型为例，取顶层、第二层和第三层厚度相同，均为167 km，第四层即底层为500 km以下区域，电导率为0.01 S/m。将上三层电导率σ=0.001 S/m时的电场幅值计算结果作为“基准”，将电导率取σ/3及3σ作为各层电导率变化的上下限，根据上述北京地磁台监测数据计算得到在对应于各层电导率变化上下限的感应地电场上下限，如图12所示。可见，相对于感应地电场“基准”值，顶层大地电导率变化导致感应地电场变化幅度接近40%，第二层大地电导率变化使得感应地电场变化不到8%，第三层大地电导率变化导致感应地电场变化不到1%。可见，当各层厚度相同时，所在层越靠近地表对感应地电场大小影响越大。根据更多大地分层模型的计算结果可得到同样的规律，此处不再复述。

图12 感应地电场变化上下限Fig.12 The upper and lower limit of electric field

4 结论

运用平面波法计算GMD感应地电场需结合深层大地电导率参数，而由于大地探测技术的局限，获得精确的深层大地电导率参数很困难，本文采用2006年12月14日至15日磁暴期间的地磁监测数据，通过GMD感应地电场对纬度、大地电导率参数等因素的敏感性研究可知：

1）对于中低纬度地区，纬度越低感应地电场幅值越小，但纬度因素对感应地电场的影响程度小于大地电导率，感应地电场在东西向及南北向分量大小关系不仅与磁暴纬度因素相关，同时与大地结构相关；

2）感应地电场随电导率的减小而增大，且各层厚度越大影响规律越明显；

3）GMD感应地电场幅值对顶层大地参数更敏感，500 km以下的大地电导率对电场影响小，电场变化程度小于7%。

[1]KAPPENMAN J G，ALBERTSON V D.Bracing for the geomagnetic storms[J].IEEE Spectrum，1990，27：27-33.

[2]KAPPENMAN J G.Geomagnetic storms and their impact on power systems[J].IEEE Power Engineering Review，1996，16：5-8.

[3]BOTELER D H，PIRJOLA R J，NEVANLINNA H.The effects of geomagnetic disturbances on electrical systems at the Earth’s surface[J].Advances in Space Research，1998，22（1）：17-27.

[4]刘连光，葛小宁，王开让，等.地磁暴侵害我国高铁和油气管道的观测研究[J].中国科学，2016，46（3）：268-275.LIU Lianguang，GE Xiaoning，WANG Kairang，et al.Observation studies of encroachment on high-speed railway and oil&gas pipelines by geomagnetic storms in China[J].China Science，2016，46（3）：268-275（in Chinese）.

[5]GAUNT C T，COETZEE G.Transformer failures in regions incorrectly considered to have low GIC risk[R].Power Tech，IEEE Lausanne，2007

[6]WILK M，VILJANEN A，PIRJOLA R，et al.Calculation of geomagnetically induced currents in the 400 kV power grid in southern sweden[J].Space Weather，2008，6（S07005）：1-11.

[7]刘林玉，谢学武.500 kV主变压器异常声音分析[J].高电压技术，2005，31（4）：85-87.LIU Linyu，XIE Xuewu.Analysis of increase of noise of 500 kV transformer[J].High Voltage Engineering，2005，31（4）：85-87.

[8]颜永强，冯玉昌，刘连光，等.地磁感应电流监测装置在西北750 kV电网的应用[J].电网与清洁能源，2008，24（6）：38-41.YAN Yongqiang，FENG Yuchang，LIU Lianguang，et al.Application of GIC monitoring device in northwest 750 kV power grid[J].Power System and Clean Energy，2008，24（12）：38-41.

[9]刘连光，刘春明，张冰，等.中国广东电网的几次强磁暴影响事件[J].地球物理学报，2008，51（4）：976-981.LIU Lianguang，LIU Chunming，ZHANG Bing，et al.Strong magnetic storm’s influence on China’s guangdong power grid[J].Chinese Journal of Geophysics，2008，51（4）：976-981.

[10]孙树敏，程艳，杨帆，等．不同纬度电网地磁感应电流水平的比较研究[J].电网与清洁能源，2013，29（1）：50-57.SUN Shumin，CHENG Yan，YANG Fan，et al.Comparison study of the geomagnetically induced current level of power grid in different latitudes[J].Power System and Clean Energy，2013，29（1）：50-57（in Chinese）.

[11]PIRJOLA R，VILJANEN A.On geomagnetically-induced currents in the finnish 400 kV power system by an auroral electrojet current[J].IEEE Transactions on Power Delivery，1989，4（2）：1239-1245.

[12]VILJANEN A，PIRJOLA R，AINM O.Magnetotelluric source effect due to 3D ionospheric current systems using the complex image method for 1D conductivity structures[J].Earth，Planets and Space，1999，51（9）：933-945.

[13]PIRJOLA R，BOTELER D H，VILJANEN A，et al.Prediction of geomagnetically induced currents in power transmission systems[J].Advances Space Research，2000，26（1）：5-14

[14]Hakkinen L，PIRJOLA R，Calculation of electric and magnetic fields due to an electrojet current system above a layered earth，Geophysica，1986，22，31-44.

[15]PIRJOLA R，VILJANEN A，BOTELER D H，Series expansions for the electric and magnetic fields produced by a line or sheet current source above a layered Earth，Radio Sci，1999，34（2）：269-280.

[16]KUAN ZHENG，RISTO J.PIRJOLA，DAVID H.Boteler，geoelectric fields due to small-scale and large-scale source currents[J].IEEE Transactions on Power Delivery，2013，28（1）：442-449.

Study on the Influence of Earth Conductivity on GMD Induced Geoelectric Field

LIU Qing1，XU Ting1，HAN Kangkang1，RONG Yajie2
（1.Xi’an University of Science and Technology，Xi’an 710054，Shaanxi，China；2.Xinjiang Electric Power Design Institute，Urumqi 830001，Xinjiang，China）

Given that the deep earth conductivity parameters are difficult to obtain，studies on the sensitivity of GMD induced electric field to the earth conductivity are of more guiding significance for the GIC assessment and prevention.In this paper，the influence of different earth models on the induced electric field is studied based on the plane wave method.The results show that the amplitude of the induced field is larger in high resistance region.The relation between east-west and north-south induced electric field is related not only to the latitude but also to the characteristics of the earth model.For the multi-layer earth conductivity model，the amplitude of induced electric field is more sensitive to the top-layer conductivity，and the influence rule is more obvious with bottom conductivity reducing.

GMD；induced electric field；earth conductivity；geomagnetic storm；geomagnetic induced current（GIC）

1674-3814（2017）06-0054-05

TM154.1

A

2017-05-23。

刘 青（1978—），女，硕士，副教授，主要从事电力系统电磁暂态计算、电磁脉冲耦合计算方面的教学及科研工作。

（编辑 张晓娟）

国家重点研发计划项目（2016YFC0800103）。

Project Supported by the National Key Research and Development Plan（No.2016 YFC0800103）.