纯电动汽车翻滚耐撞性拓扑优化设计*

宋洁 雷正保

（长沙理工大学）

根据各个国家的交通事故数据统计结果分析，尽管翻滚事故在交通事故中所占的比例很小，但是致死率却极高。随着车辆C-NCAP星级评价体系的完善，人们对车辆碰撞安全性要求的提升，人们对翻滚碰撞安全性的要求也越来越高，汽车翻滚安全已成为研究热点。传统的提高翻滚碰撞安全性的方法包括，依靠经验和类比，采用强度更高的材料，对骨架构件进行尺寸优化以及局部加强优化，其变量仅局限于形状和尺寸（如截面尺寸及厚度等），很难对原始的结构进行较大改进，而且采用增加钢材厚度的方法会导致汽车的质量增加[1]。为了克服这些不足，为提高车辆翻滚碰撞安全性提出一种全新的设计方法，文章以某品牌纯电动车为原型，以车身结构刚度最大化为目标，建立白车身耐撞性拓扑优化数学模型，按法规FMVSS 208中的翻滚方法对纯电动汽车车身进行拓扑优化，提取了拓扑构型并进行了动态翻滚试验，验证了纯电动汽车翻滚耐撞性拓扑优化设计方法的可行性。

1 耐撞性拓扑优化方法

1.1 基于混合元胞自动机的拓扑优化方法

由于汽车碰撞是一个复杂的过程，属于瞬时、高速及大变形的非线性问题，包含材料、几何非线性、元素间的接触及应变率等效应，因此需要建立能代表碰撞过程这一复杂行为的优化模型。混合元胞自动机优化方法作为一种不需要计算灵敏度的变密度拓扑优化算法，能够有效解决瞬态非线性的连续拓扑优化问题。它能根据有限元应力的计算结果，确定设计域内单元材料对整体结构刚度的贡献率，将贡献率大的单元材料保留，贡献率小的单元材料删除，确定结构在具有最大刚度时材料的最佳分配方案，从而将结构的最优化问题转化成寻求材料的最佳分布问题[2-5]。在混合元胞自动机的约束当中，通常采用质量或体积作为优化目标[6]。基于元胞自动机可建立如下的数学优化模型。

Si*——设定的内能密度值，kg/mm3；

xi——元素密度，kg/mm3；

vi——元素体积，mm3；

M*——设定的质量，kg；

N——设计区域中材料元素的数量；

M，C，K——质量、阻尼、刚度矩阵；

d——位移，mm；

t——时间，s。

Si*值在元胞自动机算法中不断更新，直到得到满意的质量结果为止。

1.2 收敛准则

收敛标准取决于不断更新的设计变量所用的设计规则的类型。文章主要将结构质量的改变作为收敛准则：

式中：M（k）——迭代到k次时结构的质量，kg；

ρi（k）——迭代到k次时元胞单元i的密度，kg/mm3。

当质量没有进一步变化的可能时，优化的过程就收敛，这个状态可表示为：

混合元胞自动机算法的数值经验显示，在一些应用中，ΔM（k）显示了一种周期行为——质量上很小的改变引起结构较大的变化，为了避免过早的汇集，收敛准则通过使用连续2次迭代的平均变化来确定，如式（4）所示。

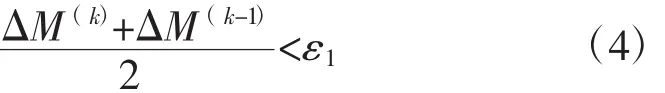
文中，ε1=0.001，当第k个循环质量分数满足要求时，材料的再分配终止。

2 纯电动汽车车身翻滚拓扑优化

2.1 汽车翻滚试验方法

通过多年的研究，汽车界已经发明了一些翻滚方法，如斜坡/螺旋坡翻滚试验、转向盘引导的翻滚试验及泥土绊翻试验等[7]。

对于车辆翻滚碰撞而言，国内外没有强制性的法规，唯一涉及乘用车翻滚的是美国FMVSS 208的平台翻车试验方法。因此文章为了更加合理科学地对车辆翻滚式碰撞加以研究，特借鉴了该试验方法。翻滚试验装置，如图1所示，试验车放在23°斜角的楔形平台车上，然后以48 km/h的速度平移，在不大于915 mm的距离内平台车从48km/h减速到0，减速度至少为20 g，持续时间至少为0.04 s[8-9]。

图1 汽车翻滚试验装置图

2.2 车身结构优化数学模型

在翻滚碰撞过程中为使车身结构变形最小，以结构的刚度最大化为目标进行优化，并将刚度最大目标转化为柔度最小问题来求解。柔度可用应变能来定义[10]，碰撞过程中结构的应变能表示为：

式中：S——应变能，J；

εf——最终应变；

σ——加载过程中从未变形状态到最终应力应变状态的应力值，Pa；

ε——应变；

U——位移矩阵；

F——力的列向量。

2.3 车身结构拓扑优化模型的建立

以某国产品牌纯电动车为原型，车身总长、宽、高分别为3 790，1 560，1 530 mm，轴距和轮距分别为2 530，1 375 mm。将汽车分为车身、轮胎及电池3个部分[11]。电池置于乘坐区里面，在整车所占据的三维体积中挖除乘员舱、行李舱、动力总成及风窗玻璃等部分，建立的三维模型，如图2所示。

图2 整车的三维模型

网格划分前对模型进行合理的简化以提高建模效率，将台车简化成带阻挡板的移动斜坡，有限元模型，如图3所示。为了使整个模型规模不至于过大以保证计算时间，将网格设为尺寸为25 mm的六面体，模型单元总数为121 978，节点总数为296 516。

图3 汽车翻滚有限元模型

2.4 拓扑优化结果及构型提取

优化区域在指定的质量分数下将被逐渐进行材料的删减以达到最优的材料分布，在碰撞过程中承力少的部位将被逐渐删除[12]。图4示出纯电动汽车车身拓扑优化试算结果。由于约束条件对最终的拓扑优化结果影响较大，首先分别选取质量分数f=0.2，f=0.4的约束条件进行试算，如图4a和图4b所示，其构型出现删除材料单元过多和过少现象，无明显的空间骨架结构特征，二者均不是最佳的材料布局方式。故重新选取质量分数f=0.3进行计算，经过60个循环迭代后结构不再出现变化，最终优化结果可以得到清晰的载荷路径，如图4c所示。对比分析3组不同质量分数优化结果，根据材料的分布对优化结果进行适当的修正后，初步确定纯电动汽车车身结构，如图5所示。

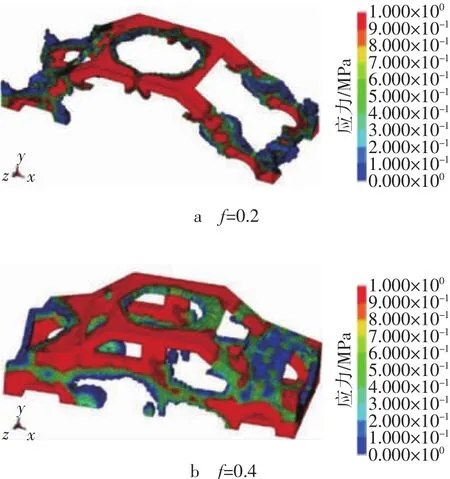
图4 纯电动汽车车身拓扑优化试算结果

图5 抽象后的纯电动汽车车身骨架结构

3 拓扑优化结果分析

3.1 顶压试验的分析

车顶抗压试验主要用于检验汽车发生滚翻事故时车顶是否有足够强度以抵抗变形，确保乘员的生存空间[13]。根据FMVSS 216车顶抗压强度法规要求：使用加载装置为762 mm×1 829 mm的金属压力板对车顶加载，如图6所示，刚性平面沿法向以小于12.5 mm/s的速度对车顶加载，整备质量不超过2 722 kg的乘用车在其1.5倍自身质量的载荷作用下，加载设备的位移不得超过127 mm。

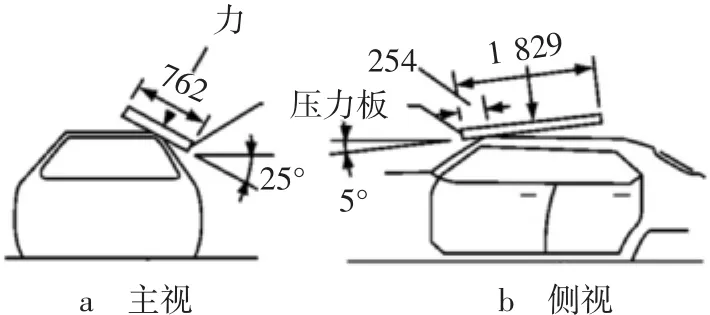
图6 车顶抗压试验示意图

仿真结果表明，在没有车门和顶盖的情况下，A柱、B柱与车顶横梁连接部分应力最大，如图7所示。

图7 顶压试验应力云图

压力板的接触力-位移曲线，如图8所示。由图8可知，当压力板对车顶所施加的载荷达到该车1.5倍整备质量时的下移量为39.4 mm，小于法规的127 mm；或者说当压力板的下移量达到127 mm时，压力板与车顶的接触力为37.64 kN，已经超过1.5倍的自身质量，证明该构型满足法规对顶部抗压强度的要求。

图8 顶压试验压力板的力-位移曲线

3.2 动态翻滚试验的分析

翻滚碰撞时车体的变形导致对乘坐室的侵入是造成乘员伤害的因素之一，又直接决定乘员的生存空间，因此乘坐室的侵入量可以很好地预测乘员的伤害程度[14]。由于翻滚是一个动态变化过程，测量乘坐室侵入量较复杂，考虑到车架部分变形很小，拟在车架中心面处设计一基准标杆，通过测量A柱、B柱与基准标杆之间距离（L）的变化情况来计算立柱的变形量，进而找出乘员乘坐区的最大变形。

图9示出汽车动态翻滚试验A柱和B柱的变形量曲线。从图9可以得到不同时间点A，B柱的变形量，其中，在0.9 s时B柱变形量达到最大（55 mm），1.3 s时A柱变形量达到最大（52 mm）。

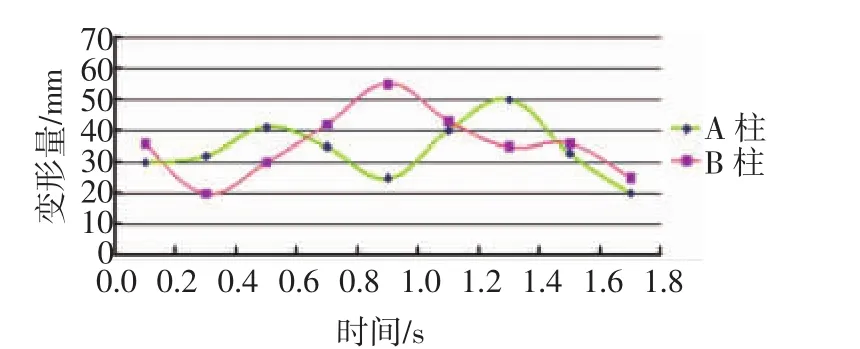
图9 汽车动态翻滚试验A柱和B柱的变形量曲线

从翻滚碰撞的整个过程来看，该纯电动汽车的整个车身骨架基本能够保持原状，没有发生太大变形，A，B柱的变形量相对于车的宽度较小，不会对乘员造成严重伤害。

4 结论

文章以电动汽车翻滚工况得出车身骨架的拓扑优化构型，其顶部抗压强度性能明显优于法规对顶部抗压强度的要求；根据动态翻滚碰撞过程中A，B柱最大变形量，翻滚耐撞性拓扑优化得出的构型在翻滚发生后能够获得足够的乘员生存空间，保证乘员安全；使用翻滚耐撞性拓扑优化方法，可以得到顶部高抗压强度和A，B柱低变形量的车身骨架构型，因此，翻滚耐撞性拓扑优化方法能够应用于汽车的正向概念设计，为后续的详细设计提供理论依据。

由于文章仅是通过有限元仿真分析验证车身骨架构型的顶压和动态翻滚性能，且有限元仿真分析存在一定误差，因此在有充足的试验条件时，还需要真实试验进一步验证仿真结果的准确性。