分布式相参雷达两种相参参数估计算法的性能比较

李京效，姜 伟，张良俊

(上海航天电子技术研究所，上海 201109)

分布式相参雷达两种相参参数估计算法的性能比较

李京效，姜 伟，张良俊

(上海航天电子技术研究所，上海 201109)

针对分布式相参雷达信号级融合的可行性问题，介绍相参融合原理，并以两节点分布式相参雷达为模型，仿真分析时延差与相位差的估计误差对SNR合成增益的影响，得到了相参性能良好条件下的参数估计精度要求。以此为依据，研究基于正交四相编码信号和OFDM-LFM信号的多种相参参数估计算法，仿真结果表明，在低目标回波信噪比下，峰值提取法优于互相关处理算法，多脉冲积累算法优于同算法下一维参数提取法，且各算法均受系统采样频率(时间测量精度)的影响，从而为多雷达间协同探测的模式选择提供了有利参考。

分布式相参雷达；时延差估计；相位差估计；信号级相参融合

0 引言

大型有源相控阵雷达由于其具有规模庞大、机动性差、制造工艺要求苛刻和造价昂贵等缺点，极大地制约了其发展与应用[1]。为了克服这些缺点，MIT林肯实验室于2003年提出了分布式相参雷达的概念[2]，并将其作为美国下一代导弹防御雷达的重要发展方向[3]。分布式相参雷达的基本思想是将多部分散的子雷达通过中心控制处理系统连接起来进行联合探测，实现信号级的相参融合处理，以达到甚至超过一个大孔径雷达的性能[4]。由于分布式相参雷达具有实现性好、效费比高、机动性强、可靠性高和扩展灵活等特点，受到了国内外的广泛关注[5]。美国雷达专家Dr.Brookner在文献[6-7]中高度评价了分布式相参雷达的实验成果。

国内关于分布式相参雷达的研究尚处于起步阶段，前期取得的初步成果主要集中在分布式相参雷达的概念介绍[8]与综述[9]、原理验证[10]、同步系统的设计[11]、正交波形的设计[12]、相参性能的监测模块设计[13]和ISAR成像[14]等方面，而在相参参数(时延差和相位差)估计方面，虽有一定的研究，但都基于特定信号形式的特定算法研究，缺乏各算法之间的比较分析。文献[15]将正交频分线性调频信号(OFDM-LFM)与峰值提取法相结合，对相参参数估计性能展开研究。文献[16-17]针对运动目标，提出了基于卡尔曼滤波的相参参数滤波算法。本文主要对基于正交四相编码信号和正交频分线性调频信号的2种相参参数估计算法进行仿真，评价各算法的估计效果，分析参数估计效果的影响因素，总结运用条件，为多雷达间协同探测的模式选择提供参考。

1 分布式相参雷达相参融合原理

分布式相参雷达[18]具有接收相参模式和全相参模式2种工作模式。

1.1 接收相参模式

在接收相参模式下，各子雷达发射正交波形，同时各子雷达的接收端含有N个匹配滤波通道，分别与子雷达1～N的发射波形相匹配。则对任意的子雷达l，第k个匹配滤波通道的输出为：

(1)

(2)

对所有子雷达所有通道补偿后的脉压信号相参叠加，即可得到接收相参模式下的综合响应

(3)

1.2 全相参模式

当相参参数估计值满足一定精度后，系统转入全相参模式。在该模式下，各子雷达发射相同波形，并利用前一阶段获得的时延和相位参数估计值对发射端进行调整，使得各路信号能够同时同相地抵达目标，实现能量的叠加。当各子雷达接收到目标反射回的信号，经下变频和匹配滤波后，再次对时延和相位参数进行估计，最后将所有子雷达补偿后的脉压信号相参叠加，即可得到全相参模式下的综合响应：

(4)

2 参数估计误差对相参性能的影响

上述SNR得益的获得受时频同步精度和相参参数估计精度这2个因素的制约。由于实际系统中各子雷达频率源提供的工作频率并非完全一致，从而导致触发信号在时间轴上存在差异，再加上初始时刻的时间差与相位差，这些因素共同构成了系统的时频同步误差，从而影响到后续的相参处理；另一方面，受系统采样频率、测量精度和算法自身的分辨率的影响，相参参数提取过程中将会存在一定的估计误差。下面主要对时延和相位估计误差对相参性能的影响进行分析。

假设分布式相参雷达系统的节点数N=2，发射波形采用正交四相编码信号，编码序列参考文献[19]，单个码元的宽度为Tp=0.1 μs，波长λ=0.1 m，子雷达1与目标的距离R1=120 km，子雷达2与目标的距离R2=120.030 02 km，目标的速度v=0 m/s，目标的回波信噪比SNR0=10 dB。同时假定，子雷达1的参数估计值准确，子雷达2的参数估计值存在误差。

2.1 时延估计误差对SNR增益的影响

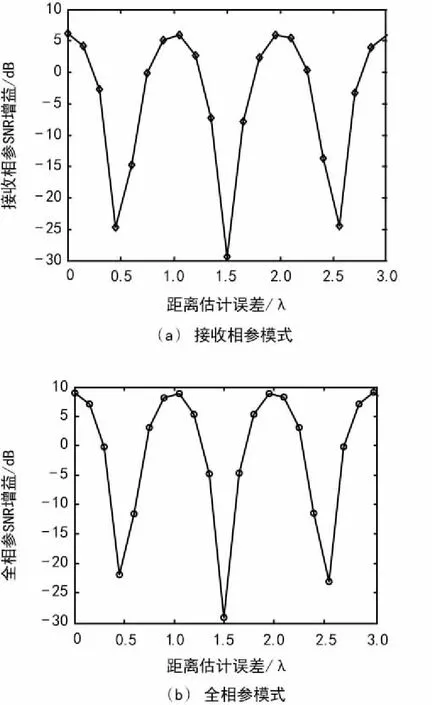
图1 时延估计误差对SNR增益的影响

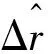
2.2 相位估计误差对SNR增益的影响

假设子雷达1和子雷达2的时延(距离)估计值准确，仅仿真分析相位估计误差对相参性能造成的影响。

图2 相位估计误差对SNR增益的影响

由图2可以看出，相位误差在0～π时，SNR增益随估计误差的增大逐步减小。当误差超过0.5π时，已不具备相参性能。同样，要想SNR增益下降值控制在1dB左右，相位估计误差应不超过0.2π。单部雷达的相位估计误差应在0.1π之内。

3 相参参数估计算法

3.1 峰值提取法

峰值提取算法的思想就是通过确定单、双基地回波脉压信号峰值的位置来计算目标相对各子雷达间的距离差和相位差，其表达式如下：

(5)

(6)

峰值提取算法是一种最为简单的参数估计算法，但该方法要求雷达系统具有灵敏的测距精度才能获取精准的时延和相位误差，进而实现良好的相参性能。峰值提取法根据单路匹配滤波通道是否进行多脉冲积累分为一维峰值提取法和多脉冲积累峰值提取法。其信号处理流程如图3所示。

图3 (一维/多脉冲积累)峰值提取法处理流程

3.2 互相关处理法

由于单、双基地回波脉压后的信号具有互相关性，互相关处理法就是将各子雷达得到的单、双基地回波匹配滤波后的结果进行互相关处理，以此来提取相参参数估计值，进而实现时延差和相位差的闭环校正。其互相关结果的峰值时刻对应着信号从各子雷达到目标的单程传播时延差Δτ(或距离差ΔR)，互相关结果的峰值相位对应着传播路程差导致的相位差Δψ。同样，根据单路匹配滤波通道是否进行多脉冲积累分为一维互相关处理法和多脉冲积累互相关处理法，其信号处理流程如图4所示。

图4 (一维/多脉冲积累)互相关处理流程

4 相参参数估计算法仿真与对比分析

4.1 各相参参数估计算法效果分析

为方便分析不同相参参数估计算法的估计效果，统一设分布式相参雷达系统的波长λ=0.1 m，信号带宽为10MHz，时间同步误差为1ns，目标的速度、目标相距子雷达1和子雷达2的距离均与第2节相同。

对于正交四相编码信号，单个码元宽度为0.1μs，其信号形式如前所述。在不同的目标回波信噪比下，各算法的时延差和相位差估计值的均方根误差(RMSE)分别如图5和图6所示。

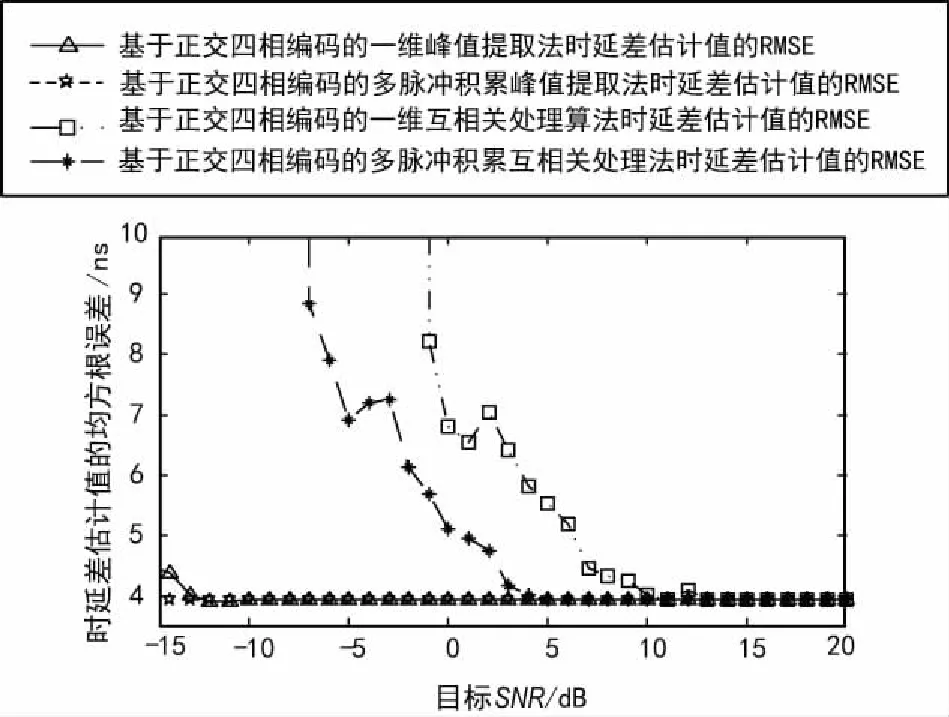
图5 各算法时延差估计值的RMSE曲线

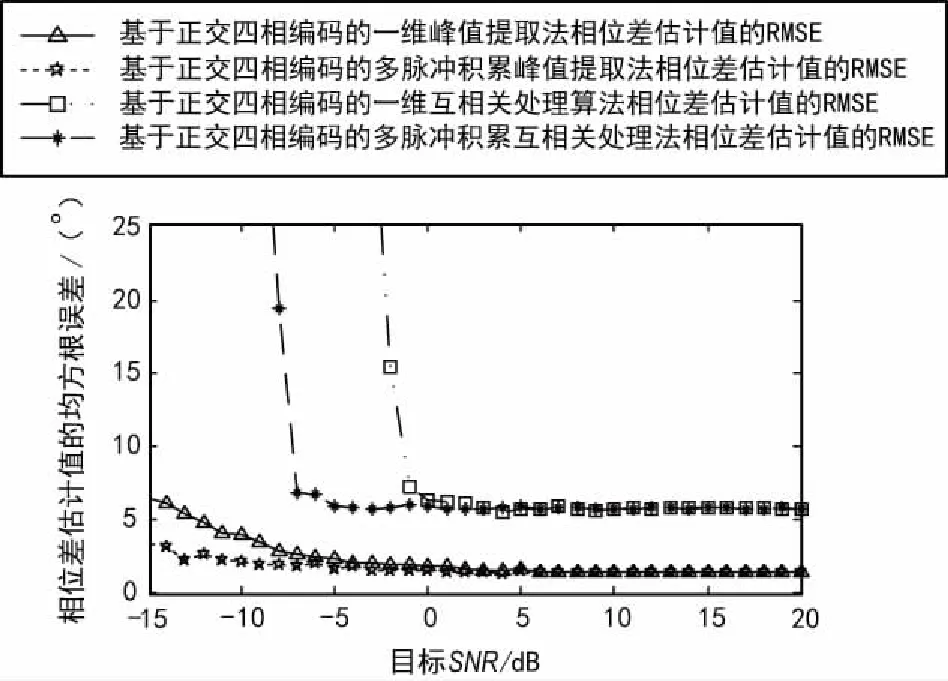
图6 各算法相位差估计值的RMSE曲线

由估计误差可以看出：① 在低SNR0下，(一维/多脉冲积累)峰值提取法优于(一维/多脉冲积累)互相关处理法，其原因在于信号的非理想正交性，使脉压结果(自相关函数)峰值含有非零成分的互相关函数值，从而影响不同匹配滤波通道脉压值间的互相关处理；② 多脉冲积累处理算法优于一维处理算法，原因在于多脉冲积累的SNR得益。

从相参性能来看，当目标回波信噪比SNR0>0 dB时，相位差估计值的RMSE趋于稳定，且满足第2节相参性能良好的控制条件(相位差估计误差小于36°)；在时延差估计方面，需要根据2种相参模式分情况讨论。对于接收相参模式，由于相参参数估计与补偿只在接收端进行，只需估计误差小于一个距离分辨单元(这里为10 ns)即可，因此，(一维/多脉冲积累)峰值提取法在整个区间满足要求接收相参的要求，而一维/多脉冲积累互相关处理算法分别在SNR0>-1 dB和SNR0>-7 dB时才能满足。而对于全相参模式，虽然SNR0>10 dB时估计值趋于稳定，但是需要各子雷达发射信号在目标处能同时同相地叠加，以第2节的仿真结果可知，对于波长为0.1 m的信号，相参性能良好条件下(SNR增益较理论值下降1 dB)，时间同步误差应不小于33 ps，参数估计误差难以保证，这就说明高分辨的时延差估计方法仍需深入的研究。

4.2 不同信号形式对相参参数估计效果的影响分析

为方便对比不同信号形式对参数估计效果的影响，对基于OFDM-LFM信号的峰值提取算法展开仿真。设发射信号脉冲宽度0.1 μs，调频带宽10 MHz，相对载频f1=0,f2=15 MHz，在接收相参模式下，第k部子雷达产生的射频信号表示为[20-21]：

(7)

式中，k取值为1或2；fc为绝对载频，与波长λ相对应。

在不同的目标回波信噪比下，时延差和相位差估计值的均方根误差(RMSE)分别如图7和图8所示。

图7 不同信号形式下时延差估计值的RMSE曲线

图8 不同信号形式下相位差估计值的RMSE曲线

由仿真结果可以看出，在时延差估计方面，2种信号形式的参数估计效果相当；在相位差估计方面，基于OFDM-LFM信号的参数估计效果略优于基于正交四相编码信号的参数估计。

4.3 采样频率对相参参数估计效果的影响分析

图9和图10说明了参数估计效果受采样频率的影响，频率越高，时延差估计值越精确。而对于相位差，在低SNR下，采样频率越高，估计误差越小；当目标回波SNR0大于某一特定值时，采样频率越高，估计误差反而较大，但均在相参性能良好的控制条件内。由此说明，分布式相参雷达的相参性能受时间(距离)测量精度的影响。

图9 一维峰值提取法参数估计值的RMSE曲线

图10 多脉冲积累互相关法参数估计值的RMSE曲线

5 结束语

分布式相参雷达在接收相参模式下可获得N2倍的SNR增益，在全相参模式下可获得N3倍的SNR增益。而相参参数估计则是影响系统相参性能的重要因素。本文以两节点雷达为模型，针对静止目标，仿真了相参参数估计误差对SNR合成增益的影响，以此为评价指标，对基于正交四相编码信号和基于OFDM-LFM信号的峰值提取法和互相关算法进行了仿真。结果表明，在低目标回波信噪比下，峰值提取法优于互相关处理算法，多脉冲积累算法优于同算法下一维参数提取法，接收相参模式较全相参模式在工程实现上更容易获得SNR得益；在信号形式的选择方面，正交四相编码信号和OFDM-LFM信号在参数估计效果上相当，实际应用时应根据系统的节点数及复杂度进行权衡；同时，参数估计精度受采样频率的影响，要获得良好的相参性能，对时延差估计与测量提出了非常高的要求。下一步，将对高分辨的时延差估计方法和运动目标的跟踪滤波技术展开研究。

[1] 姜伟.MIMO雷达信号处理关键技术研究[D].北京：北京理工大学，2009.

[2] ROBEY F C,BELCGER M,BUDGE M,et al.Next Generation Radar Study Result[R].MIT Lincoln Laboratory,2003.[3] COUTTS S,CUOMO K,MCHARG J,et al.Distributed Coherent Aperture Measurements for Next Generation BMD Radar[C]∥IEEE Workshop on Sensor Array and Multichannel Signal Processing,2006:390-393.

[4] MCHARG J,CUOMO K,COUTTS S,et al.Wideband Aperture Coherence Processing for Next Generationg Radar[R].MIT Lincoln Laboratory,2004.

[5] GAO H W,CAO Z,LU Y B,et al.Development of Distributed Aperture Coherence-synthetic Radar Technology[C]∥2013 IET International Radar Conference,Xi’an,China,2013:638-642.

[6] BROOKNER E.Phased-array and Radar Breakthroughs[C]∥2007 IEEE International Radar Conference,2007:37-42.

[7] BROOKNER E.Phased-array and Radar Astounding Breakthroughs(An Update)[C]∥2008 IEEE Internaitonal Radar Conference,2008:1-6.

[8] 史仁杰.新一代弹道导弹防御雷达-分布式相参合成孔径相控阵雷达[J].航天雷达,2011,28(2):1-6.

[9] 张亚婷.新体制雷达-分布式孔径相参合成雷达[J].火控雷达技术,2014,43(2):43-47.

[10] 高红卫,曹哲,鲁耀兵.分布式阵列相参合成雷达基本研究与原理验证[C]∥第十二届全国雷达学术年会论文集，2011:129-134.

[11] 曾涛,殷丕磊,杨小鹏，等.分布式全相参雷达系统时间与相位同步方案研究[J].雷达学报，2013,2(1):105-110.

[12] 殷丕磊,张洪纲,刘泉华，等.基于修正代价函数的分布式全相参雷达正交波形设计方法[J].计算机工程与应用,2014,50(S1):497-502.

[13] 孙培林,汤俊,张宁.分布式相参雷达相参性能的两种监控算法[J].清华大学学报,2014,54(4):419-424.

[14] 王锐.分布式全相参雷达参数估计及ISAR成像方法研究[D].北京:北京理工大学,2015.

[15] 宋靖,牛朝阳,张剑云.分布式全相参雷达正交频分LFM信号设计及性能分析[J].中国科学,2015,45(8):968-984.

[16] 殷丕磊,张洪纲,翟腾普，等.基于Kalman滤波的分布式全相参雷达相参参数估计方法[J].北京理工大学学报,2016，36(3):282-288.

[17] 殷丕磊.地基宽带分布式全相参雷达技术研究[D].北京:北京理工大学,2016.

[18] FLETCHER A S,ROBEY F C.Performance Bounds for Adaptive Coherence of Sparse Array Radar[C]∥Proceedings of the Adaptive Sensor Array Processing Workshop,MIT Lincoln Laboratory,2003.

[19] DENG Hai.Polyphase Code Design for Orthogonal Netted Radar System[J].IEEE Transactions on Signal Processing.2004,52(11):3 126-3 135.

[20] 刘波.MIMO雷达正交波形设计及信号处理研究[D].成都:电子科技大学,2008.

[21] 李昀豪，王佩，唐斌.一种对MIMO雷达正交QPSK信号的参数估计方法[J].现代雷达，2015,37(10):29-33.

Performance Comparison between Two Coherent Parameters Estimation Algorithms for Distributed Aperture Coherent Radar

LI Jing-xiao,JIANG Wei,ZHANG Liang-jun

(ShanghaiAerospaceElectronicTechnologyInstitute,Shanghai201109,China)

Aiming at the feasibility of signal coherent processing for distributed aperture coherent radars,the principle of coherent integration is introduced.Based on a two-node distributed aperture coherent radar system,the influences on SNR gain caused by time delay estimation errors and phase estimation errors are analyzed.Through the simulation,good coherent parameters estimation accuracies are obtained.Furthermore,several coherent parameter estimation algorithms based on orthogonal four-phase-coded signal and OFDM-LFM signal are studied.The simulation results show that the peak extraction algorithm is superior to the cross-correlation algorithm,and the multi-pulse accumulation algorithm is superior to the one-dimension parameter estimation algorithm.All these studies provide helpful reference for the operation mode selection of multi-site radar cooperative detection.

distributed aperture coherent radar;time delay offset estimation;phase offset estimation;signal coherent integration

10.3969/j.issn.1003-3106.2017.09.07

李京效,姜伟,张良俊.分布式相参雷达两种相参参数估计算法的性能比较[J].无线电工程,2017,47(9):32-37，43.[LI Jingxiao,JIANG Wei,ZHANG Liangjun.Performance Comparison between Two Coherent Parameters Estimation Algorithms for Distributed Aperture Coherent Radar[J].Radio Engineering,2017,47(9):32-37，43.]

TP391.4

A

1003-3106(2017)09-0032-06

2017-01-05

李京效 男，(1990—)，硕士研究生。主要研究方向：分布式雷达技术。

姜 伟 男，(1980—)，博士，高级工程师。主要研究方向：雷达系统设计、MIMO雷达信号处理。