空间应力重积分技术在水工混凝土复杂结构配筋中应用

□萧燕子 梁春雨 许昌

（黄河勘测规划设计有限公司）

空间应力重积分技术在水工混凝土复杂结构配筋中应用

□萧燕子 梁春雨 许昌

（黄河勘测规划设计有限公司）

文章基于Ansys软件提供的二次开发平台，实现了非杆件体系三维有限元分析中空间应力重积分程序的研发，设计了任意截面形状和任意空间放置两种类型的算例对开发方法和程序进行了验证，最后总结了空间应力重积分技术开发的基本步骤和编程要点，为其它用户进行相关开发提供借鉴和参考。

Ansys；二次开发；应力积分

1 引言

水工建筑物多数为形体复杂或尺寸比例特殊结构（如蜗壳、尾水管、地下洞室、大体积混凝土孔口等），无法将结构简化为常规梁、板、柱基本构件，需要利用弹性应力进行结构强度设计。通用和专业结构分析有限元软件具有丰富的梁（杆）系模型结构内力图输出功能，极大地提高了结构分析和设计工作效率；但是对形体复杂和空间整体性较强的特殊结构进行有限元分析，有时不得不采用空间实体单元，它较梁（杆）系模型能更准确地反映结构的几何形式和实际受力状态。实体单元的使用，会衍生一个新的问题：空间应力重积分问题。当前，商用有限元软件均无法解决这一难题，因而结构应力分析在结构强度设计中的应用受到一定程度的限制。

文章研究成果成功解决了三个问题：一是空间任意位置截面应力重积分；二是空间任意形状截面应力重积分；三是积分所用应力符合现行标准《水工混凝土结构设计规范》（SL191-2008）第12.2.1条“计算钢筋面积时，按主拉应力在配筋方向投影图形总面积”要求。文章为弹性力学问题向结构力学问题转换架起了一座桥梁，丰富大型软件的功能应用。

2 数值积分理论

通过三维有限元分析，得到结构体内任一点的空间应力场，一点的应力状态可以由应力分量来表示：

在已知以上六个分量的情况下，可以推求经过P点的任一斜面上的应力。为此，在P点附近取一个平面ABC，平行于这一斜面，并与经过P点而平行于坐标面的三个平面形成一个微小的四面体PABC，见图1：

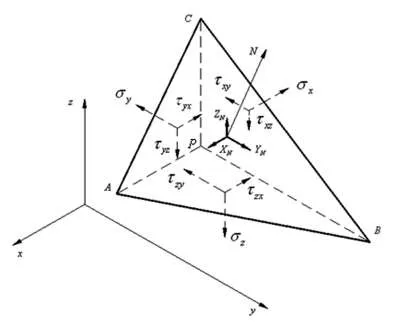
图1 空间点的应力状态图

命平面ABC的外法线为N，其方向余弦为：

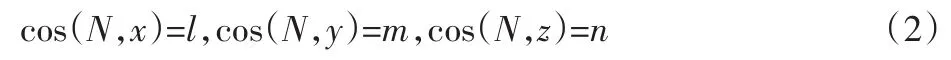
三角形ABC上的全应力SN在坐标轴方向的分量用XN、YN、ZN代表，根据力的平衡关系，可得任一Gauss点3个坐标方向的应力分量为：

设三角形ABC上的正应力为σN，可由投影关系得：

根据剪应力互等定理，将上式代入下式：

三角形ABC上的全应力SN而剪应力为τN，则由于

截面内力为

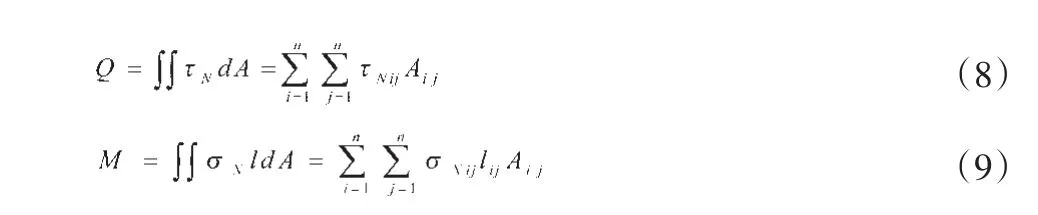
式中：lij为积分点（i，j）到截面积分轴之距，Aij为积分点（i，j）控制面积。

3 程序流程和编程概要

3.1 程序流程

在Ansys平台下，进行应力重积分一般要分四步进行：获取应力场结果、空间截面选取（空间三点坐标）、应力转换和应力积分，程序流程图如图2所示。

图2 空间应力重积分流程图

3.2 编程概要

Ansys的二次开发工具主要有四个，即APDL、UPFS、UIDL及Tcl/Tk。其中APDL作为ANSYS参数化设计语言，具有参数定义、数值计算、流程控制、宏程序与子函数的使用、数据文件的输入输出等功能。能满足应力重积分相关计算。积分几何要素如图3所示。程序设计时需要注意的几个方面：一是积分截面：空间平面用三点坐标来描述；二是积分轴：积分轴为积分平面内一条线，知道方向即可，位置可用程序自动搜索，也可事先给出；三是空间方向识别：弯矩有顺逆时针，剪力在平面内有正交两个方向，轴力拉压区分；四是应力重积分：采用空间重积分技术，对积分截面重新划网，借助数值积分的概念，对全截面进行积分，对于复杂形状截面，要考虑积分轴位置自动搜索的需要，以及动态数组相关技术。

图3 积分几何信息图

4 算例验证

悬臂梁梁长L=10 m，受均布荷载P=10 kN/m2，梁截面有矩形、箱形、T形和工形4种；对梁固支端截面内力进行理论解与数值解求证，计算结果见表1。从表中可知，各截面下内力数值解和理论解相同。计算结果说明，无论多么复杂的截面形状，本程序均适用。

表1 四种截面梁梁端内力理论值与计算值对比表

悬臂梁梁长L=10 m，受均布荷载P=10 kN/m2，梁截面为矩形b=1.50 m，h=2 m，位于空间π平面上；对梁固支端截面内力进行理论解与数值解求证，计算结果见表2。从表中可知，各截面下内力数值解和理论解相同。进一步说明，任意空间位置的截面，程序均适用。

表2 π平面放置梁内力理论值与计算值对比表

5 结论

根据Ansys提供的二次开发平台，利用弹性力学、空间几何、向量代数、理论力学基本原理方法，成功实现了非杆系体系空间应力重积分程序的开发。为了验证方法和程序的正确性，文章设计了具有解析解的悬臂梁模型进行数值模拟计算，结果表明，文章的数值解与理论解十分吻合。另外，文章研究成果能满足最新国家标准，拓展了有限元在水工结构复杂异形块体建筑物仿真分析中的应用。

TV331

B

1673-8853（2017）07-0079-02

2017-04-12

编辑：符蕾

萧燕子（1986—），女，工程师，主要从事水利水电工程设计工作。