基于卷积神经网络的手写数字识别

李斯凡，高法钦

(浙江理工大学信息学院， 杭州 310018)



基于卷积神经网络的手写数字识别

李斯凡，高法钦

(浙江理工大学信息学院， 杭州 310018)

在LeNet-5模型的基础上，改进了卷积神经网络模型，对改进后的模型及网络训练过程进行了介绍，推导了网络模型训练过程中涉及到的前向和反向传播算法。将改进的模型在MNIST字符库上进行实验，分析了卷积层不同滤波器数量、每批数量、网络学习率等参数对最终识别性能的影响，并与传统识别方法进行对比分析。结果表明：改进后的网络结构简单，预处理工作量少，可扩展性强，识别速度快，具有较高的识别率，能有效防止网络出现过拟合现象，在识别性能上明显优于传统方法。

卷积神经网络；手写数字；识别；LeNet-5

0 引 言

手写数字识别是利用机器或计算机自动辨认手写体阿拉伯数字的一种技术，是光学字符识别技术的一个分支[1]。该技术可以应用到邮政编码、财务报表、税务系统数据统计、银行票据等手写数据自动识别录入中。由于不同的人所写的字迹都不相同，对大量的手写体数字实现完全正确地识别不是一件简单的事情。随着全球信息化的飞速发展和对自动化程度要求的不断提高，手写体数字识别的应用需求急迫[2]，因此,研究一种准确又高效的识别方法有着重要的意义。

传统的识别方法如最近邻算法[3]、支持向量机[4]、神经网络[5-7]等，对复杂分类问题的数学函数表示能力以及网络的泛化能力有限，往往不能达到高识别精度的要求，随着科技的发展和科学研究的不断深入，卷积神经网络[8-10](convolutional neural networks，CNNs)的出现为解决这个问题提供了可能，它最初由美国学者Cun等[11]提出，是一种层与层之间局部连接的深度神经网络。作为深度学习中最成功的模型之一，其已成为当前图像识别领域的研究热点。但研究发现，卷积神经网络在识别训练过程中会出现过拟合现象。本文详细介绍了基于LeNet-5进行优化改进的卷积神经网络模型及其算法的实现过程，在算法的实现部分加入惩罚项，避免过拟合现象发生。在此基础上，分析了不同网络参数对识别的收敛速度和性能的影响。与传统方法相比，本文的改进模型减少了预处理工作量，同时还有效避免了人工提取特征的不足，提高了识别率和鲁棒性。

1 卷积神经网络

卷积神经网是一种主要用于二维数据处理的深度神经网络模型，它能够学习大量输入与输出之间的映射关系。由卷积层和采样层交替组成，每一层有多个特征图，卷积层的每一个神经元与上一层的一个局部区域相连，这种局部连接使网络具有更少的参数，有利于训练。通过卷积层的运算，可以使原信号特征增强并且降低噪声。通过采样层降低特征图的分辨率并抽样出图片的显著特征，使模型具有抗噪能力，在保留图像有用信息的同时又降低了特征的维度。

1.1 LeNet-5网络模型

LeNet-5是典型的卷积神经网络模型，网络包含输入一共有8层，除去输入和输出，中间的连接层C1到F6可看成是隐含层，输入层由32×32个感知节点组成，接着是交替出现的卷积层和抽样层，C1是第一个隐藏层也称卷积层，进行卷积运算，S2层是采样层，实现抽样，C3作为第三隐藏层，进行卷积操作，然后经隐藏层S4进行二次抽样，其后是三个神经元(节点)数分别为120、84、10的全连接层。LeNet-5网络模型结构如图1所示。

图1 LeNet-5结构

1.2 卷积神经网络模型结构设计

对原始的LeNet-5模型进行如下改进：在LeNet-5网络中，激励函数是双曲正切函数，现将sigmoid函数作为网络的激励函数，使网络各层的输出均在[0,1]范围内，并去掉C5层，直接将经S4二次采样的特征图与F6以全连接的方式连接，同时改变各层神经元的个数。具体模型结构如图2所示，对比改进前后的模型可以看到，改进后的网络隐含层只有5层，模型神经元数量减少了很多，具有更少的参数，所以训练的时间也会大大的缩短，同时由于改进后的网络依旧是卷积层和采样层交替出现，所以改进的网络仍保留了图像对位移、缩放和扭曲的不变性和良好鲁棒性的优点。

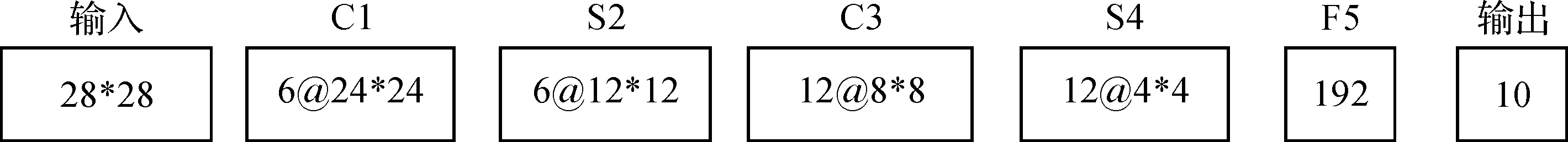
图2 改进的网络模型结构

模型结构中，输入层输入规格为28×28的手写数字图片，接下来是交替出现的卷积和采样层，C1层是第一个卷积层，该层有6个24×24的特征图，这一层特征图中的每个神经元是输入的图像与一个5×5卷积核进行卷积操作，然后经过激活函数输出形成的，在卷积时，同一特征映图上的神经元权值相同，网络可以并行的学习，卷积层的结果作为下一层(即S2层，也称采样层)的输入，S2层特征图中的每一个神经节点与C1层中相应的特征图以2×2的区域相连，经过采样层后特征图的个数不变，但输出大小在两个维度上都缩小2倍。C3是第2个卷积层，S4是第2个采样层，其后连接的是单层感知器，将S4层的12个特征图展开，最后是与S4层以全连接的方式相连得到输出的输出层，含有10个节点对应10种输出类别,整个CNN网络模型一共有3966个参数,与LeNet-5模型的60000个参数相比，参数个数大大减少。

1.3 卷积神经网络训练算法

1.3.1 网络训练过程

网络模型的训练过程可分为两个阶段：

第一阶段，前向传播：

a)在开始训练前，建立网络并进行初始化设置，设置网络层数以及卷积核大小，用小的随机数对所有权值进行初始化，设置学习率和迭代次数，选定训练样本和测试样本集；

b)然后将训练样本(x，y)输入网络，通过各层网络得到输出t。

第二阶段，反向传播：

a)计算实际输出与相应的理想输出的均方误差；

b)反向传播对权值参数优化，通过梯度下降法，计算网络中误差对权值的偏导数，调整权值矩阵，更新权值和偏置，不断进行迭代直到满足预先设定的迭代次数要求，训练完成。

1.3.2 算法实现

下面对训练中的相关算法的具体实现进行介绍，实验中用l表示当前层，那么当前层的输出可以表示为：

xl=f(ul),ul=Wlxl-1+bl

(1)

其中：ul为l层(当前层)的输入；Wl为l层特征图的权值；xl-1为上一层的输出；bl为当前层的额外偏置(也称基)；f为激活函数，实验中将sigmoid函数作为激活函数。

使用卷积核对上一层的特征图进行卷积，然后通过激活函数，得到卷积层的输出特征图。卷积层的计算形式如式(2)所示：

(2)

采样层中，对上一卷积层的特征图进行下采样，采样后输入输出特征图数量不变，其计算形式如下：

(3)

其中：n表示从卷积层到抽样层的窗口大小，Mj表示选择的输入特征图的集合。

对单个样本(x，y)，它经网络产生的误差可用代价函数表示，如式(4)所示：

(4)

网络在前向传播过程中，使用每个训练样本的误差的总和表示全部训练集上的误差，对于m个训练样本((x1,y1),(x2,y2)，…，(xm,ym))的误差，可用平方误差代价函数表示：

(5)

为了防止网络出现过拟合，实验时在平方误差代价函数中加入惩罚项：

(6)

其中：yi表示第i个样本的理想输出。ti表示第i个样本对应网络的实际输出。 第一项是均方差项，用来表示代价函数，第二项是权重衰减项，用来减小权重的幅度，防止过度拟合。λ为权重衰减参数 ，用于控制公式中两项的相对重要性。

在反向传播过程中，对层l的每个神经元对应的权值的权值更新，需要先求层l的每一个神经节点的灵敏度，那么对于第n层(输出层)每个神经节点根据式(7)计算灵敏度：

(7)

激活函数的具体函数形式为：

(8)

对式(8)求导可得：

(9)

因此输出层的灵敏度可表示为：

(10)

对l=n-1,n-2,…,2的各个层，当前层l每个神经节点i对应的灵敏度计算公式如下：

(11)

将式(11)中的n-1与n替换为l与l+1，就可以得到：

(12)

那么l=n-1,n-2,…,2的各个层的灵敏度为：

δl=Wl+1δl+1xl(1-xl)

(13)

那么各层中误差对W和b的偏导数就可以表示如下：

(15)

最后就可以按照如下公式对层l中的参数W和b进行调整和更新，其中η表示学习率：

(16)

(17)

实验通过识别率来度量手写字符的识别结果，识别率计算公式如下：

误识别率/%=错误识别个数/样本总数×100

(18)

2 实验结果及分析

2.1 实验数据

实验所用的数据来自MNIST手写数字字符库，该字符库中含有0～9的训练数据集和测试数据集两种图片，包括60000个样例的训练样本集和10000个样例的测试样本集，每张图片的灰度级是8，大小为28*28，图3为部分样本，分别从MNIST字符库的训练样本集和测试样本集中随机抽取2000个和1000个样本作为本实验中的训练样本和测试样本。

图3 字符库部分样本

2.2 实验结果分析与讨论

由于训练样本较多，无法实现一次性将全部样本输入到网络，因此采取分批次输入，使网络得到充分训练，为研究每批输入到网络中的样本数量对识别率的影响，分别将单次输入网络的样本图片数量设置为一批输入50、100、200，得到的实验结果如图4所示。

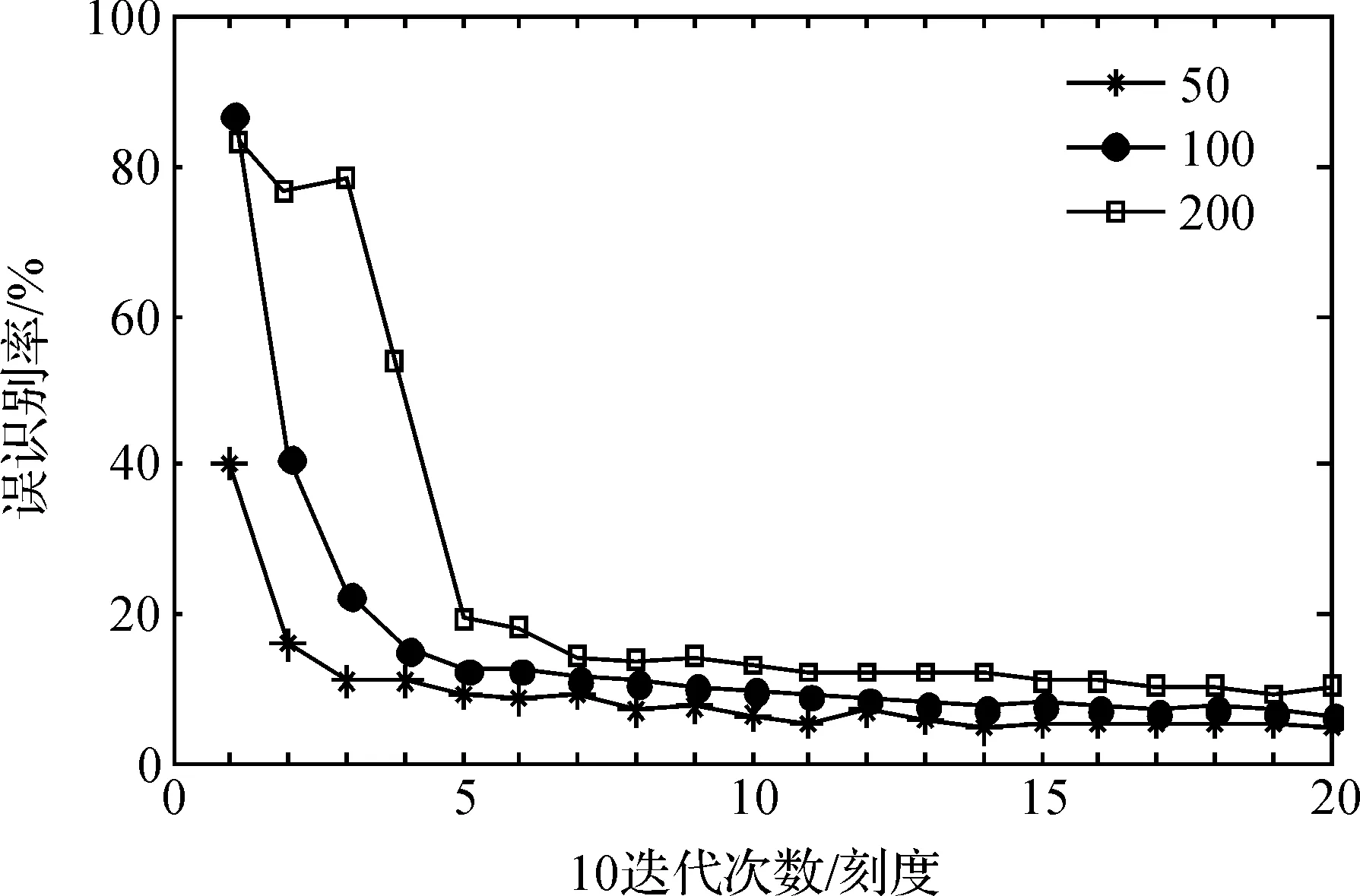
图4 每批输入样本数量对识别性能的影响

图4中，横坐标表示网络训练过程中的迭代次数,纵坐标表示测试样本集的误识别率。从图4中可以看出，随着迭代次数的增加，误识别率逐渐减小，网络逐渐达到收敛状态，当每批输入50个样本到网络时，迭代30次左右就可以取得较高的识别率，识别效果明显，对样本训练时，单次输入样本数量越少，网络收敛速度越快，同时误识别率比单次输入100和200个样本都要低。

在训练样本、测试样本数量相同，每批输入的样本数也相同的情况下，对网络的规模进行调整，分别将卷积层C1和C2的滤波器数量设置为2和8、6和12、10和16，测试网络规模对泛化性能的影响，图5为对训练集和测试集数据使用不同网络规模进行识别的结果。

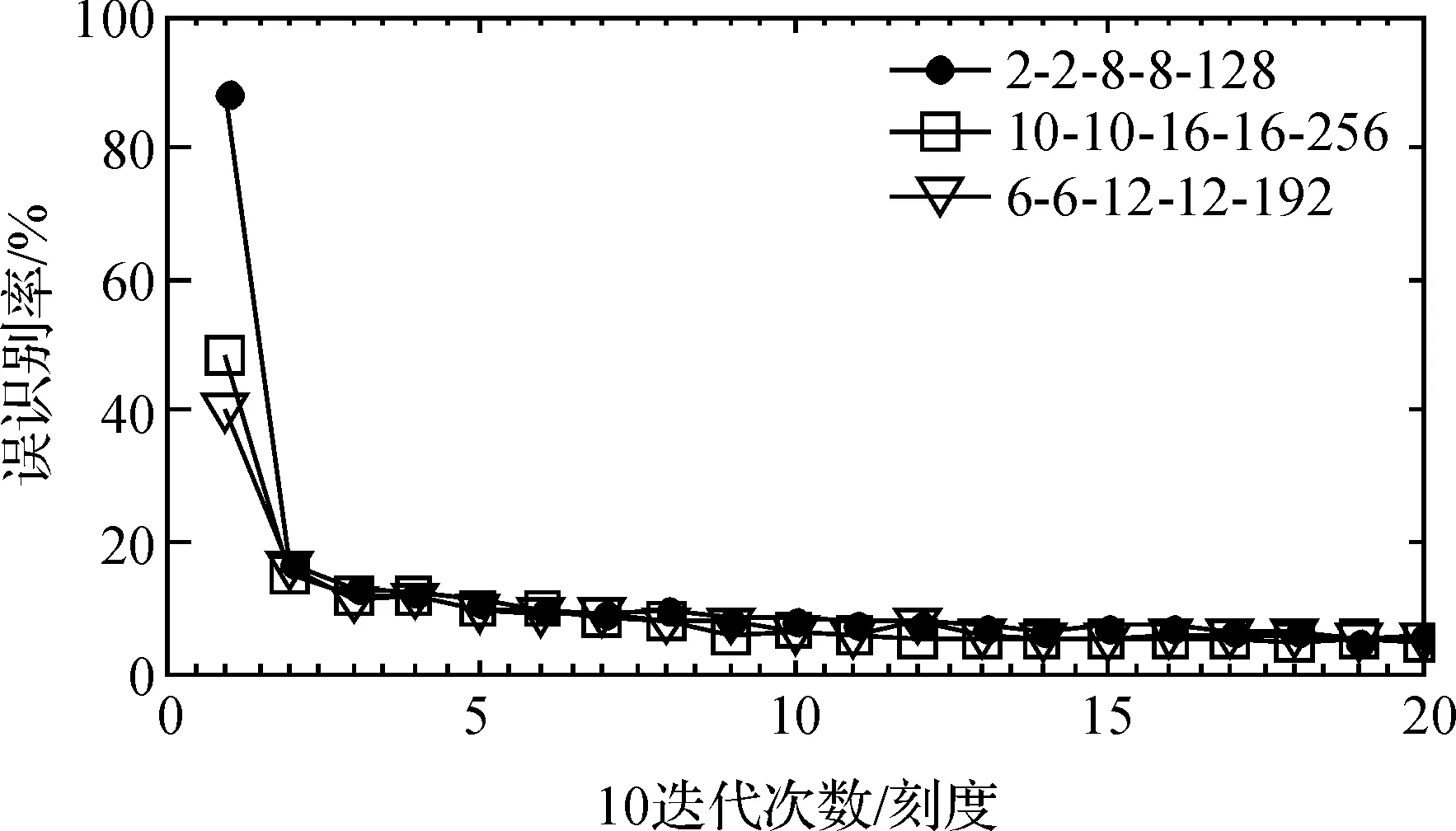
图5 网络规模对识别性能的影响

从图5中可以看出，在迭代30次以后，可达到高于90%的识别率，随着迭代次数增加，不同网络规模对样本的识别率越来越高，但变化不大，可认为这时网络达到收敛，取得最佳识别效果，网络结构为6-6-12-12时，收敛速度最快，识别效果也比较好，这是因为这时的网络规模在2000个训练样本下能得到充分训练。同时，网络性能达到一定程度后，继续增加网络中各层的规模，网络也可以较快的收敛，但对识别率影响不大，这是因为网络规模增大后，相应需要学习的参数也增加了，网络要充分训练需要的样本相应也会增加，而实验中的2000个训练样本可能无法满足实际训练要求，使网络无法得到充分训练，实验表明，减小网络规模，网络的泛化能力有降低趋势，但增加网络规模，网络的泛化能力并没有明显的提高，但仍具有较强的稳定性能和可扩展性。

如果学习率设置不合理，会使网络陷入局部极小值，导致无法收敛，出现过拟合现象。为分析网络学习率对网络识别结果的影响，分别将网络学习率设置为0.2、0.5、1.0、1.2、2.0，实验结果如图6所示。

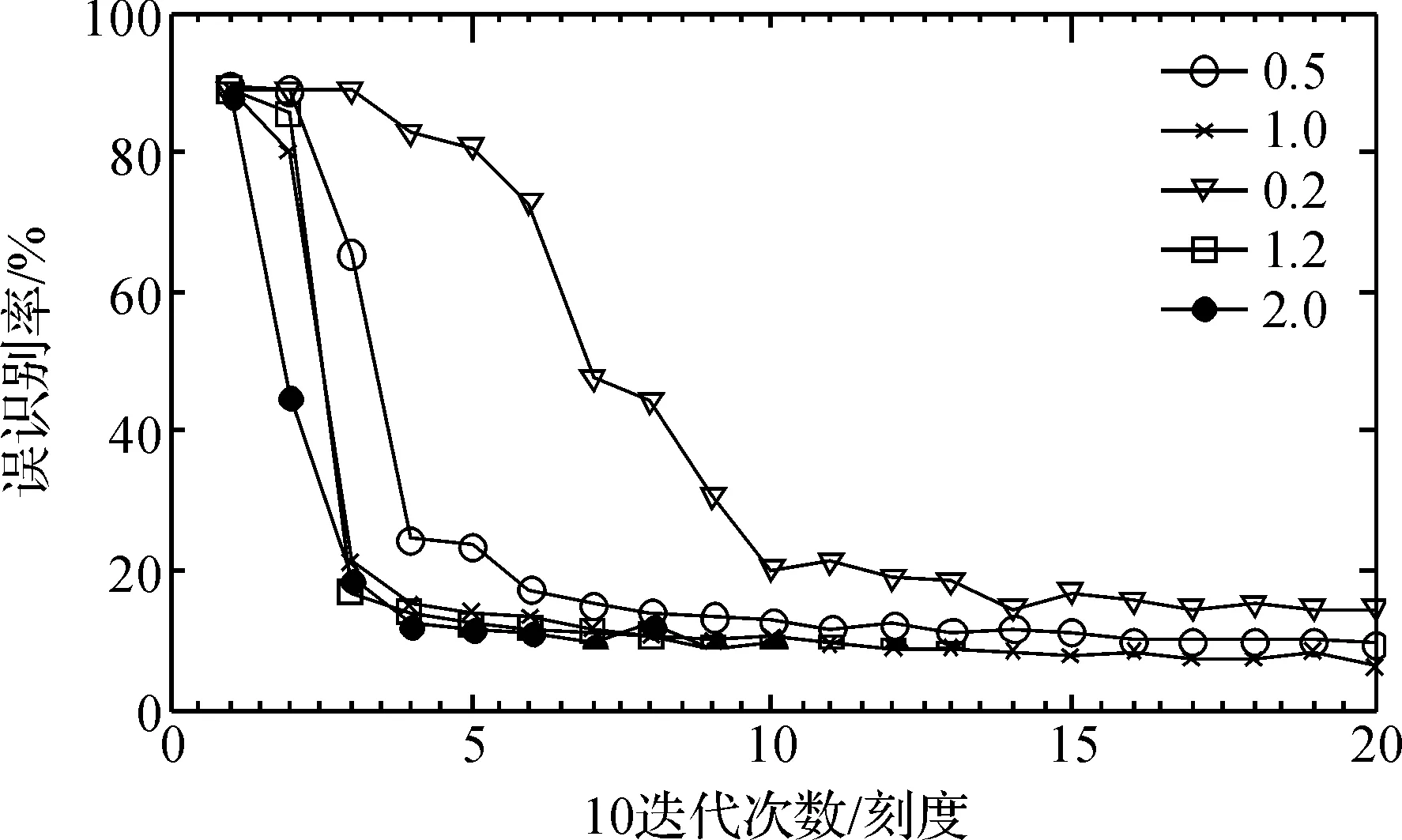
图6 不同学习率下的识别结果

从实验结果可以看出：网络学习率越大，收敛速度也越快，网络识别率相对高一些，当学习率取值为2.0时，开始网络识别率会下降的很快，随着迭代次数增加，识别率很高，但会出现在一个值附近上下波动，不稳定,这是学习率取值过大，学习的速度较快引起的。可以看到识别曲线平稳下降，没有出现过拟合现象。

在式(4)中已经详述了训练样本在前向传播过程中产生的误差，本文建立的网络模型，在不同学习率下，样本集在网络中训练产生的均方误差如图7所示。

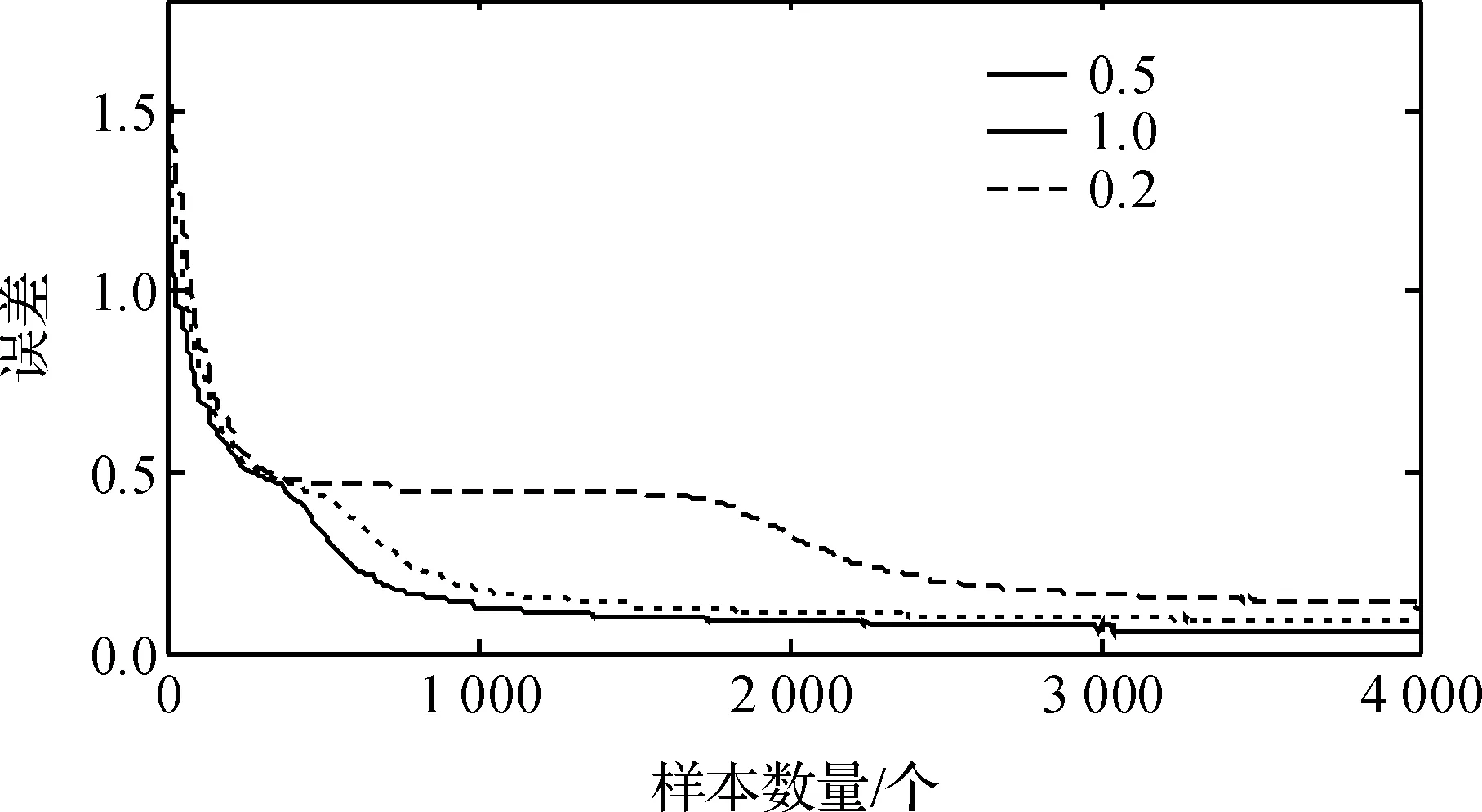
图7 网络在不同学习率下训练的误差曲线

在图7中，横坐标表示训练样本的数量，纵坐标表示计算得到的均方误差，对网络用几个不同的学习速率进行训练，从训练后误差变化曲线可以看出，在训练过程中,随着输入样本数量的增加，均方误差逐渐减小，直到网络达到一个较稳定的值。随着训练的进行，当学习率取值为1.0时，均方误差下降的速度比0.2和0.5时要快，学习率取0.2时，均方误差的曲线在一段时间变化比较平稳，收敛速度相对较慢，这是学习率取值偏小的缘故，随着样本数量的增加，收敛速度越快，识别效果也越好。

为了分析CNN网络的识别性能，利用几种常用的识别方法对MNIST字符库进行识别，结果如表1所示。

表1 几种常用方法识别结果

从表1可以看出，卷积神经网络模型在MNIST手写数字字符库上的误识别率为0.98%，和其它识别方法相比，其误识别率更低，表明此方法在手写体数字识别方面具有一定的优势。

3 结 语

本文对LeNet-5神经网络模型进行了改进，改进后的网络模型结构简单，具有更少的参数，使得网络在相同训练集上训练消耗的时间更短。由于本文建立的网络中间层是卷积层和采样层的交替出现，在网络中添加或减少网络层数容易实现，网络灵活性好，具有很强的扩展性，网络结构可以根据实际需要进行调整，以满足实际识别要求，与其它常用的分类方法相比，具有明显的优势。研究结果表明，改进后的网络能够很好地提取输入数据特征，识别率较高，惩罚项的加入消除了网络识别过程中的过拟合现象。同时，通过对识别性能的研究还发现，每批输入样本数量越小，其识别率越高，网络收敛速度越快，识别性能越好。减少卷积层滤波器数量，对应的网络规模变小，网络的泛化能力会下降，但增加网络规模，网络的泛化能力没有太大变化。

本文的研究可为后续在识别方面卷积神经网络模型结构的设计提供参考。基于卷积神经网络的识别要取得良好的效果，往往需要大量的训练样本，但在实际分类问题中，难以获取到大量的样本，在样本数量有限的情况下，如何提高网络的识别性能还有待进一步研究。

[1] 关保林,巴力登.基于改进遗传算法的BP神经网络手写数字识别[J].化工自动化及仪表,2013,40(6):774-778.

[2] 马宁,廖慧惠.基于量子门神经网络的手写体数字识别[J].吉林工程技术师范学院学报,2012,28(4):71-73.

[3] BABU U R, CHINTHA A K, VENKATESWARLU Y. Handwritten digit recognition using structural, statistical features and k-nearest neighbor classifier[J]. International Journal of Information Engineering & Electronic Business,2014,6(1):62-68.

[4] GORGEVIK D, CAKMAKOV D. Handwritten digit recognition by combining SVM classifiers[C]// The International Conference on Computer as a Tool. IEEE,2005:1393-1396.

[5] 杜敏,赵全友.基于动态权值集成的手写数字识别方法[J].计算机工程与应用,2010,46(27):182-184.

[6] 刘炀,汤传玲,王静,等.一种基于BP神经网络的数字识别新方法[J].微型机与应用,2012,31(7):36-39.

[7] ZHANG X, WU L. Handwritten digit recognition based on improved learning rate bp algorithm[C]// Information Engineering and Computer Science (ICIECS), 2010 2nd International Conference on IEEE,2010:1-4.

[8] BARROS P, MAGG S, WEBER C, et al. A multichannel convolutional neural network for hand posture recognition[C]//International Conference on Artificial Neural Networks. Springer International Publishing,2014:403-410.

[9] 宋志坚,余锐.基于深度学习的手写数字分类问题研究[J].重庆工商大学学报(自然科学版),2015,32(8):49-53.

[10] 吕国豪,罗四维,黄雅平,等.基于卷积神经网络的正则化方法[J].计算机研究与发展,2014,51(9):1891-1900.

[11] CUN Y L, BOSER B, DENKER J S, et al. Handwritten digit recognition with a back-propagation network[C]// Advances in Neural Information Processing Systems 2. Morgan Kaufmann Publishers Inc.,1990:396-404.

(责任编辑： 陈和榜)

Handwritten Numeral Recognition Based on Convolution Neural Network

LISifan,GAOFaqin

(School of Information Science and Technology, Zhejiang Sci-Tech University, Hangzhou 310018, China)

The convolution neural network model is improved on the basis of LeNet-5 model. The improved model and the network training process are introduced, and forward and back propagation algorithms of network model in the process of training are deduced. The improved model is tested on the MNIST character library, and the effects of different filter number at the convolution layer, quantity of each batch and network learning ratio on the performance of the final recognition are analyzed. Meanwhile, and the traditional identification methods are compared with the recognition method in this paper. The experimental results show that the improved network structure is simple, with small workload of pretreatment, strong extensibility, fast recognition and high recognition rate. It can effectively prevent the network over-fitting phenomenon. The recognition performance is significantly superior to traditional methods.

convolution neural network; handwritten numbers; recognition; LeNet-5

10.3969/j.issn.1673-3851.2017.05.021

2016-09-16 网络出版日期：2017-01-03

浙江省自然科学基金项目(LY14F030025)；国家自然科学基金项目(61402417)

李斯凡(1991-)，女，湖北鄂州人，硕士研究生，主要从事深度学习及大数据分析方面的研究。

高法钦，E-mail: gfqzjlg@126.com

TP391.4

A

1673- 3851 (2017) 03- 0438- 06