一题多解与学生能力训练

何海聪

《基础教育课程改革綱要》中明确指出：基础教育课程改革的具体目标之一就是要“改变课程实施过于强调接受学习，死记硬背机械训练的现状，倡导学生主动参与、乐于探究、勤于动手，培养学生搜集和处理信息的能力、获取新知识的能力、分析和解决问题的能力以及交流与合作的能力”。一题多解是实现这个目标的一种有效途径。

“一题多解”就是启发和引导发学生从不同角度、不同思路，用不同的方法，去分析解答同一道数学题的练习活动。通过这种教学模示不仅可以开拓学生思路，发展学生智力，还可以培养学生思维的灵活性和发散性以及相互合作的能力，从而提高学生综合应用知识解答数学问题的技能。

例：红星小学师生在去年植树活动中，共栽杨树和柳树500棵，其中杨树是柳树2/3，杨培养树和柳树各栽多少棵？

请同学们认真读题，仔细思考。各小组认真讨论一下，看看同学们能用几种方法解答？

有学生很快提出用方程解。

一、用方程解：

有学生答道。

解：设栽柳树X棵。

X+2/3X=500

X=300

杨树的棵数是：300×2/3=200（棵）

又有同学提出比例分配问题解。

二、用比例分配问题解

“用比例分配解”。你又是怎样想的？

学生随着学生的提问，

同学们答道：“因为杨树是柳树的2/3。就是把柳树的棵树平均分成3份，杨树就想当于柳树的2份，把栽树的总棵数就平均分成了5份，再把栽树的总棵数看作单位‘1，杨树占总棵数的2/5”柳树占总数的3/5。

三、“用归一法解”，我们又是怎样分析的？

随着老师的参与，学生分分举手答道。

“杨树是柳树的2/3，也就是说把柳树的棵数平均分成了3份，杨树的棵数就相当于柳树的2份，所以栽树的总棵数就平均分成了5份，根据已知条件，就可求每份的棵数，从而可分别求出杨树和柳树各是多少棵。”

四、用正比例解

“谁又能分析一下用正比例解的依据。”

同学们思考片刻后接着回答：

“因为杨树是柳树的2/3，我们可以把杨树的棵数和柳树棵数的比看成2：3。设杨树为X棵，则柳树的棵数为500-X棵。根据正比例的意义和比例的基本性质知识解答。”

解法四：

设栽杨树X棵，则柳树的棵数为500-X棵。

X/500-X=2/3

3X=1000-2X

X=200

柳树的棵数为500-200=300（棵）

“一题多解”这种教学模式不仅适用应用题，而且对一些四则运算试题和几何图形的面积、体积的计算也适用。

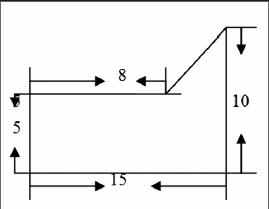
例如：计算下面多边形面积：（单位：厘米）

方法一：分割法。将计算多边形面积转化成计算我们学习过的其他图形的面积之和。

解法一：

将这个多边形转化一个三角形和一个长方形面积之和。

15×5+10-5×15-8÷2

=75+5×7÷2

=92.5（平方厘米）

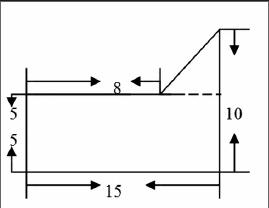
解法二：

还可以转化为一个三角形一个梯形面积之和。

10×（15-8）÷2+（15+8）×5÷2

=35+57.5

=92.5（平方厘米）

解法三：

也可以转化为三个三角形面积之和等。

8×5÷2+15×5÷2+10×（15-8）÷2

=20+37.5+35

=92.5（平方厘米）

方法二：添补法。将计算多边形面积转化成计算我们学习过的其他图形的面积之差。

如：将这个多边形添补成一个长方形，再用长方形面积减去一个梯形面积等方法。

15×10-（15+8）×（15-10）÷2

=150-57.5

=92.5（平方厘米）

总之，“一题多解”这种教学模式”“改变课程实施过于强调接受学习，死记硬背机械训练的现状，体现了以学生为主体，教师为主导的教学方式，还在一定程度上使学生体验了从不同角度，应用不同知识，不同思路，不同的方法解决同一个问题，达到殊途同归的效果。所以“一题多解”这种教学模式是提高学生 获取新知识的能力和分析解决问题的能力，以及交流与合作的能力的一种有效途径。