基于能量等效原理的应变局部化分析:II.有限元解法1)
武守信魏吉瑞杨舒蔚
∗(西南交通大学土木工程学院桥梁系,成都610031)†(交通隧道工程教育部重点实验室,成都610031)
固体力学
基于能量等效原理的应变局部化分析:II.有限元解法1)
武守信∗,†,2)魏吉瑞∗,†杨舒蔚∗,†
∗(西南交通大学土木工程学院桥梁系,成都610031)†(交通隧道工程教育部重点实验室,成都610031)
以非局部塑性理论为基础,应用状态空间理论,通过局部和非局部两个状态空间的塑性能量耗散率等效原理,提出了一种求解应变局部化问题的新方法,以得到与网格无关的数值解.针对二维问题的屈服函数和流动法则导出了求解非局部内变量的一般方程,并提出了在有限元环境中求解应变局部化问题的应力更新算法.为了验证所提出的方法,对1个一维拉杆和3个二维平面应变加载试件进行了有限元分析.数值结果表明,塑性应变的分布和载荷--位移曲线都随着网格的变小而稳定地收敛,应变局部化区域的尺寸只与材料内尺度有关,而对有限元网格的大小不敏感.对于一维问题,当有限元网格尺寸减小时,数值解收敛于解析解.对于二维剪切带局部化问题,数值解随着网格尺寸的减小而稳定地向唯一解收敛.当网格尺寸减小时,剪切带的宽度和方向基本上没有变化.而且得到的塑性应变分布和网格变形是平滑的.这说明,所提方法可以克服经典连续介质力学模型导致的网格相关性问题,从而获得具有物理意义的客观解.此模型只需要单元之间的位移插值函数具有C0连续性,因而容易在现有的有限元程序中实现而无需对程序作大的修改.
应变局部化,非局部塑性,内尺度,网格相关性,有限元
引言
岩土材料在接近破坏或断裂之前会出现高度局部化的塑性变形.这一现象不仅出现在脆性材料的破坏过程中,也出现在金属和其他聚合物材料的破坏过程中[111].一般这些材料在破坏之前,局部化的塑性变形使得材料在断裂之前呈现一条或几条带状区域,通常叫做剪切带.在剪切带形成和扩展的过程中还伴随有应变软化,即材料在加载方向的承载力随着变形的增加而减小.对剪切带局部化的数值模拟可以预测材料破坏的位置、最大变形、以及材料在断裂之前承载力随变形增大逐渐减小的全过程.这对于理解这类材料的破坏机理、预测岩土边坡和路基的失稳破坏、提高建筑物基础和隧道开挖过程中的安全性具有重要的工程意义.
然而,基于经典连续介质力学理论的剪切带局部化数值模拟会导致具有网格相关性的结果[1216].经过30多年的研究,目前广泛认为经典连续介质力学采用逐点描述材料行为的方式,没有包含材料的内尺度信息,导致描述应变软化过程的微分方程失去强椭圆性[1718],而相应的边值问题变得不适定.因此经典连续介质力学不适合描述高度不均匀的变形.
为了克服网格相关性,学者们提出了很多理论或模型.其中非局部塑性模型通过在屈服函数中引入材料内尺度,克服了连续介质力学的根本缺陷.然而,一般非局部塑性模型在应用中仍然出现了与网格相关的数值模拟结果[19].虽然Vermeer和Brinkgreve[20]、Str¨omberg和Ristinmaa[21]以及L¨u等[2223]先后提出和发展了混合非局部塑性模型并得到了与网格无关的解,但到目前为止,对于一般非局部塑性模型导致数值结果与网格相关的内在原因仍缺乏进一步的研究.
一般非局部塑性模型由Ba˘zant和Lin[24]于1988年首先提出.它源于Eringen[25]的非局部连续介质力学理论.Nilsson[26],Borino等[27],de Sciarra[28]从热动力学和最大塑性耗散功方面论证了非局部塑性模型符合热力学第一和第二定律.然而实际应用上并没有达到最初提出这一模型的目的.这说明,基于非局部塑形模型矫正网格相关性的机理还未能得到深入理解,因而有深入研究的必要.
在文献[29]中,作者以一般非局部塑性理论为基础,并应用状态空间理论,通过局部和非局部两个状态空间的能量等效提出了一种求解应变局部化问题的新方法.应用这一方法可以得到与网格无关的结果.文献[29]给出了理论框架并得到了一维问题的解析解.本文给出二维问题的一般列式和有限元解法,并给出一维问题的数值结果和二维问题的数值算例.
本文组织如下:第1节给出二维问题的屈服函数,软化规律和流动法则在两个状态空间的一般列式;第2节导出非局部内变量的求解方法;第3节给出有限元解法和应力积分算法;第4节给出一维问题的数值结果并和解析解比较,并且给出二维剪切带的数值算例;第5节得出结论.本文的工作基于小变形假设.
1 两个状态空间的屈服函数和流动法则
在局部状态空间中,如果域Ω中一点x的应力状态满足屈服准则
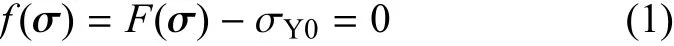
则材料在x点开始屈服,即x∈Ωp,其中Ωp代表包括所有屈服材料点的区域;F(σ)为等效应力,σY0表示初始屈服应力,σ代表该点的应力矢量,例如,对于二维问题,如果初始屈服后紧跟着应变软化,则假定在局部状态空间中,塑性变形服从关联的正交流动法则

(1)应变软化是一种满足下列条件的全局行为
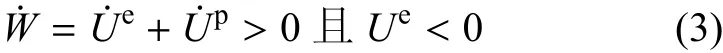
(2)屈服应力σY为非局部内变量˜η在非局部状态空间的特征塑性区域Ωcp上的积分的函数.这里的Ωcp不同于局部状态空间中的Ωp.
为了简便且不失一般性,本文只考虑J2塑性的各向同性软化,对于随动软化和各向异性软化,只要遵循局部和非局部状态空间塑性能量耗散率相等的原则,均可以导出类似的方程.非局部状态空间的屈服条件和软化规律通过下式引入
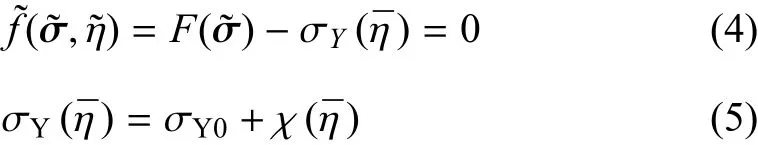
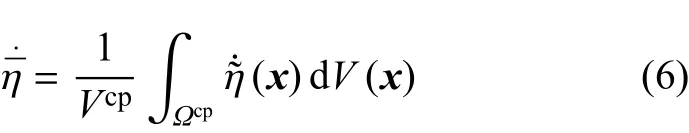
其中Vcp为特征塑性区域Ωcp的体积,并且对于二维区域,有

其中Acp代表二维特征塑性区域的面积,t为厚度.
应该指出,Ωcp是非局部状态空间的特征塑性区域,它的大小取决于材料内尺度和权函数的具体形式.

其中,¯Eps是非局部软化模量,¯Eps<0.上标“ps”代表塑性软化(plastic softening).对于非线性软化,本文暂不涉及.由于本文后面的本构关系方程均为增量形式,因此,文中的方法容易应用于非线性软化.因为非局部状态空间的应力状态与局部状态空间相应的应力状态相同,方程(5)还可以写为
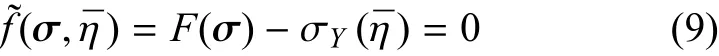
塑性加载和卸载遵循Kuhn-Tucker互补条件[32]
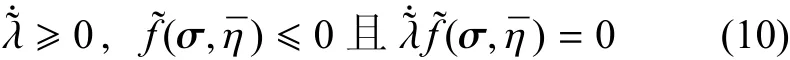
以及一致性要求


将式(5)和式(9)代入到式(12)得到
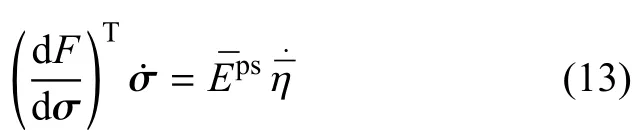
其中

因为卸载过程中应力是减小的,假设在某一时刻有一弹性试应力σtr(参看文献[32]),则˙σ可以表示为
˙σ=re˙σtr(15)
其中re是一个待确定的系数.将式(15)和式(14)代入式(13)得到
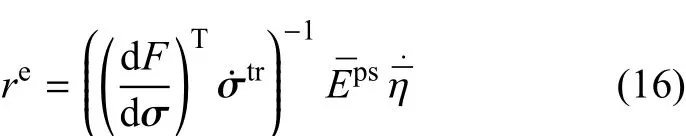
相应的弹性应变率为
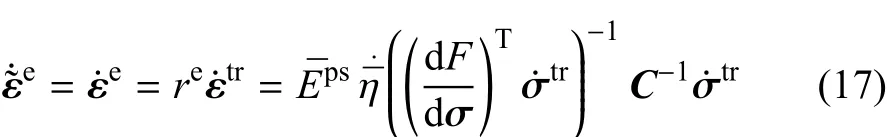
假设在非局部状态空间中,关联正交流动法则仍然适用,则有
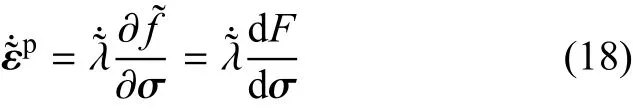
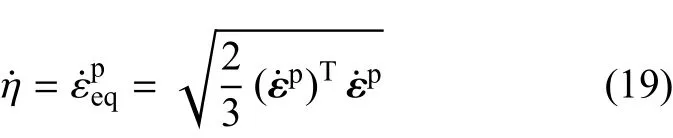
将式(2)代入式(19),对于vonM ises和Drucker-Prager屈服函数,则有

其中,γ为常数.对于vonM ises屈服函数,容易证明

对于其他类型的屈服函数,γ可能并非常数,但本文的推导过程仍然适用.为方便起见,本文只考虑von M ises屈服准则,在后面的推导中取˙η=˙λ.类似地,在非局部状态空间对于von M ises屈服函数可以证明
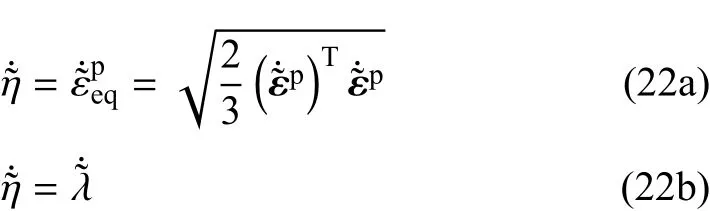
根据文献[29]中式(7b)可知,在局部状态空间的域Ωp内的塑性能变化率为
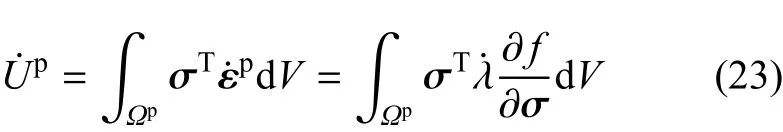
其中正交流动法则式(2)已经被引入到上式中.注意到只是流动法则而非软化律被引入到了局部状态空间.由于σ和˙λ(∂f/∂σ)在区域Ωp是连续的,对等式(23)右边应用积分中值定理可得

其中,xm为Ωp中的某点;(xm)代表(x)在Ωp中的平均值;Vp为Ωp的体积;对于二维情况,有Vp=tAp,其中t为材料的厚度,Ap为Ωp的面积.合并式(23)和式(24)可得
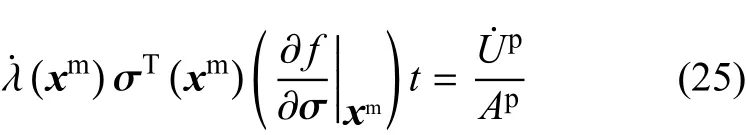
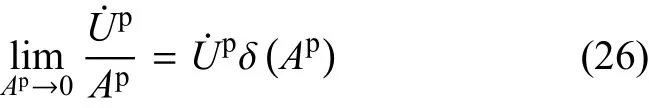
其中δ(Ap)为二维空间的Dirac-δ函数,定义如下
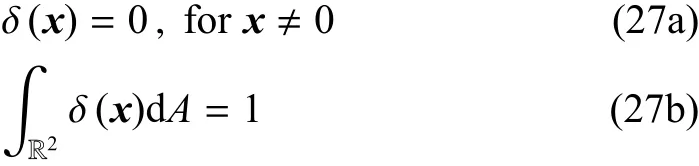
其中R2表示二维欧几里得空间.因此式(25)可以写为
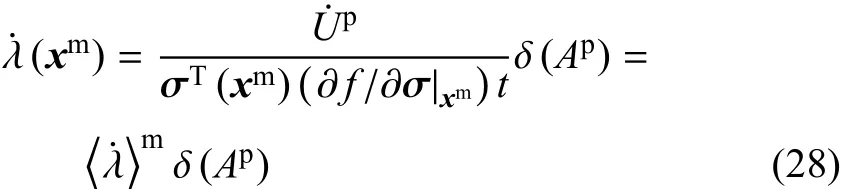
其中
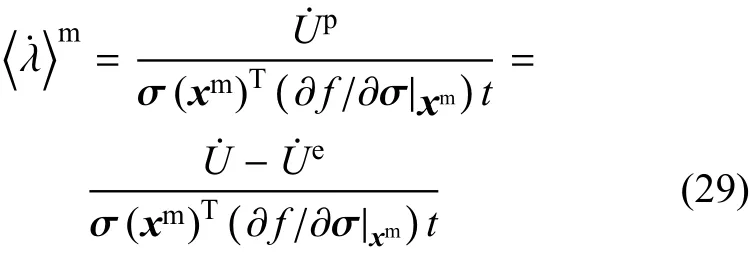
根据式(22b)和式(23),将式(28)和式(29)代入文献[29]中的式(19)可得
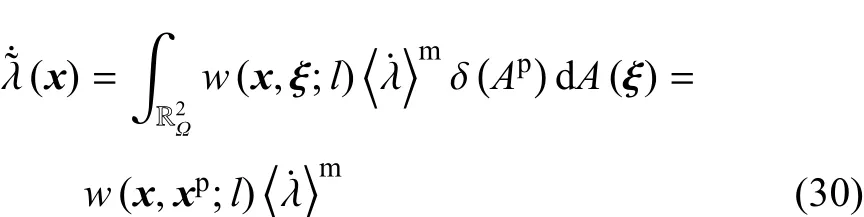
其中xp代表塑形区域Ωp中的某点.再将式(22b)和式(30)代入文献[29]中的式(27)得
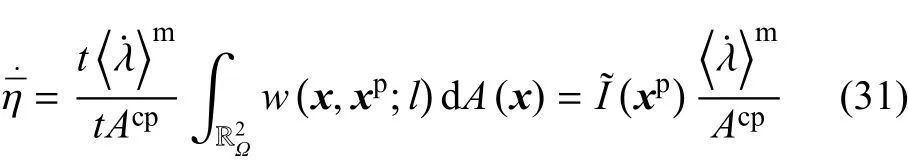
其中
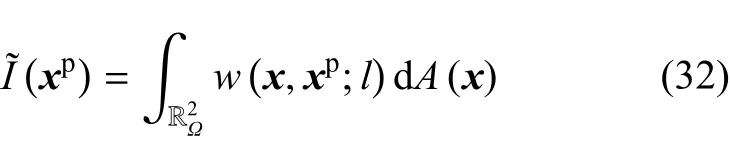
从式(29)、式(31)以及式(32)可以看出,当局部状态空间的塑性乘子为Dirac-δ函数时,非局部状态空间的非局部塑性乘子及其在特征塑性区域中的平均值具有明确定义.
2 非局部内变量的求解
将式(17)和式(18)分别代入文献[29]中的式(15a)和式(15b),然后再代入文献[29]中的式(15c)和式(16),并考虑到本文的式(30),可以得到非局部状态空间的总能量变化率为
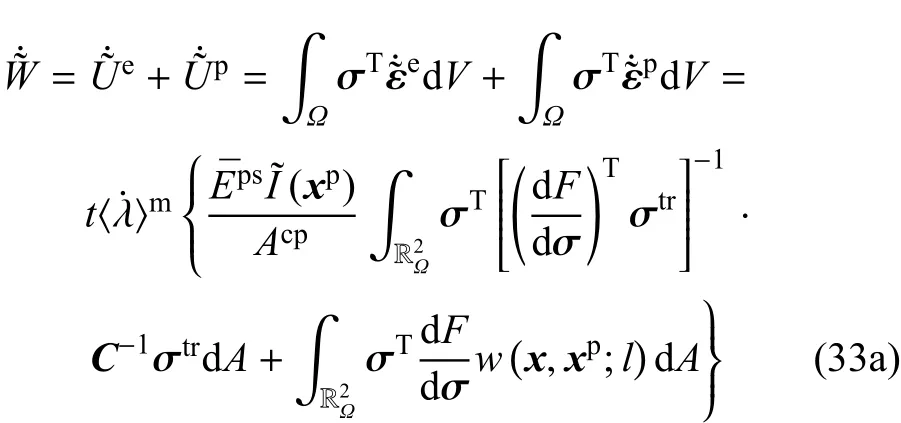
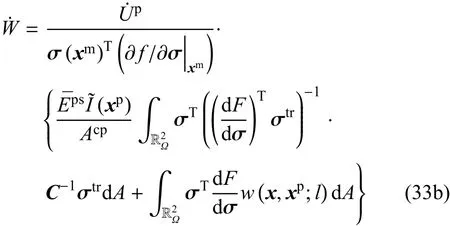
令
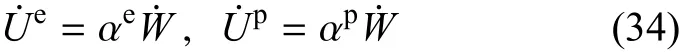
则有

将式(34)和式(35)代入式(33b),得到

其中,αe和αp分别称为弹性内能比例和塑性内能比例.由不等式(3)可知,对于应变软化,有αe<0和αp>1.将式(34)~式(36)代入式(29),可得到〈〉m如下
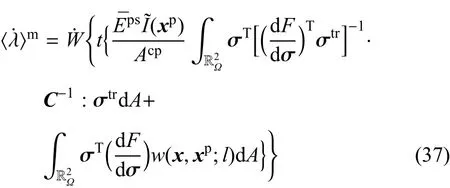
3 有限元解法
对于一维问题,采用本文的模型和方法可以得出解析解.详见文献[29].对于二维及三维应变局部化问题,本文所提出的模型和方法只能用有限元方法获得数值解.由于有限元的应变和位移场列式和平衡方程的建立与常规过程并无差异,故本文不作详述,只列出与本构方程和能量方程有关的算法.为了将注意力集中于由应变软化引起的局部化变形过程,假定载荷达到最大值后开始应变软化过程.为了保证整个计算过程中边界条件的一致性,在弹性阶段和塑性软化阶段,加载均由位移控制.弹性阶段的响应可通过常规的有限元方法获得,在弹性分析中并不应用本文所提出的方法.
3.1 局部状态空间中屈服单元的监测
在变形局部化的模拟中,通常假定某些边界保持固定,而在另外某些边界施加位移控制的载荷.假定在边界∂u0Ω上位移保持为零(其中u0代表零位移边界),在边界∂u1Ω施加位移向量ˆu∂u1Ω(u1代表非零位移边界,且∂uΩ=∂u1Ω∪∂u0Ω).并且假定在当前时间tn,材料体的状态在局部空间完全确定.在下一个时间tn+1,即(n+1)级加载步,在边界∂u1Ω上施加位移增量

其中,i代表边界N∂u1Ω上的节点号,N∂u1Ω代表边界∂u1Ω上的节点总数,∆βn+1是第n+1级加载步的增量载荷参数.在方向ˆu∂u1Ω的合力增量为
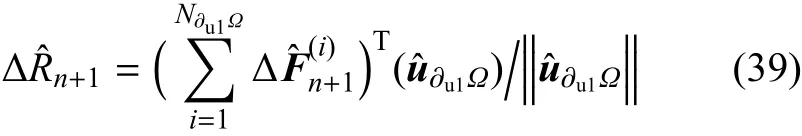
当满足条件

则全局应变软化开始,变形局部化开始发生,具有高度塑性变形的剪切带将域∂Ω划分为若干部分.令e代表单元编号,如果单元e的高斯积分点在局部状态空间的应力状态满足条件
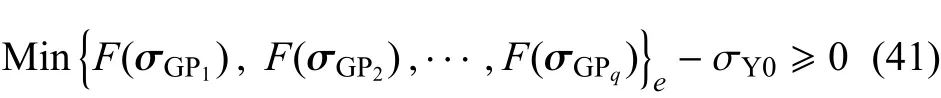
则该单元成为屈服单元.其中,下标“GP”代表高斯积分点,q代表单元e中高斯积分点的最大编号.换句话说,只要单元e内的任何一个高斯积分点满足初始屈服条件,它就被视为屈服单元.与局部状态空间相关联的塑性功将集中于这些屈服的单元内,局部内变量将通过非局部权函数从这些屈服单元映射到非局部状态空间,从而成为非局部内变量计算的基础.
3.2 非局部状态空间各分量的计算
当材料经历应变软化时,假定在时刻tn,材料的状态在局部状态空间已经由
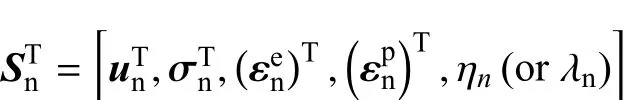
确定,在非局部空间由
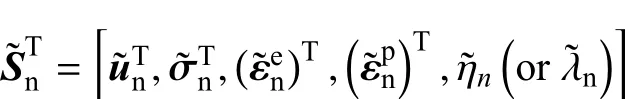
确定,并且满足平衡条件.在时刻tn+1的目标是,当在边界∂u1Ω上施加位移增量时,将状态更新到tn+1时的状态根据虚功原理,如果将上一时刻tn加载结束后对应于边界∂u1Ω上的位移总量的反力作为已经平衡的力(注意,边界∂gΩ上没有力),并且把在时间tn+1施加的位移增量作为虚位移,那么局部状态空间中外力虚功的变化为
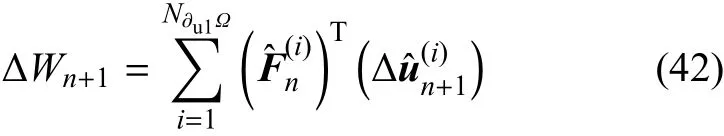
为了得到非局部状态空间相应的内力虚功,首先需要得到在(n+1)加载步的弹性内能和塑性内能的比例和这可以通过类似于导出式(33)和式(36)的过程来实现.

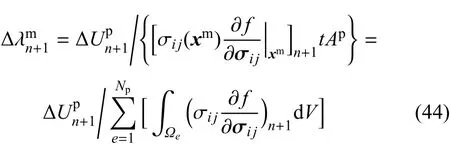
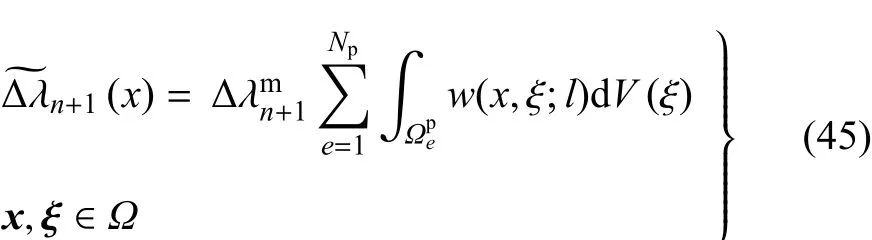
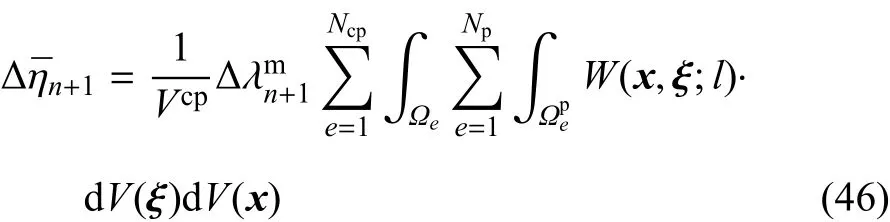
其中Vcp是与非局部状态空间相关联的特征塑形区域的体积,Ncp代表Vcp中单元的总数.Vcp的具体值与权函数相关,将在后面的数值算例中讨论.在tn+1时刻,非局部内变量的全量值更新为

将式(45)代入式(18)中得到非局部塑性应变增量为

在非局部状态空间中,弹性内能、塑性内能以及总虚功的增量为
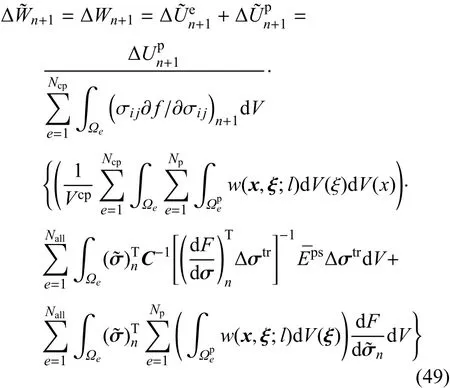
其中Nall代表Ω中的单元总数.上式还可以写为
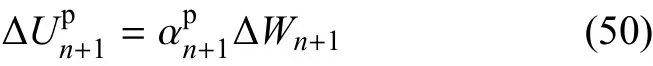
其中
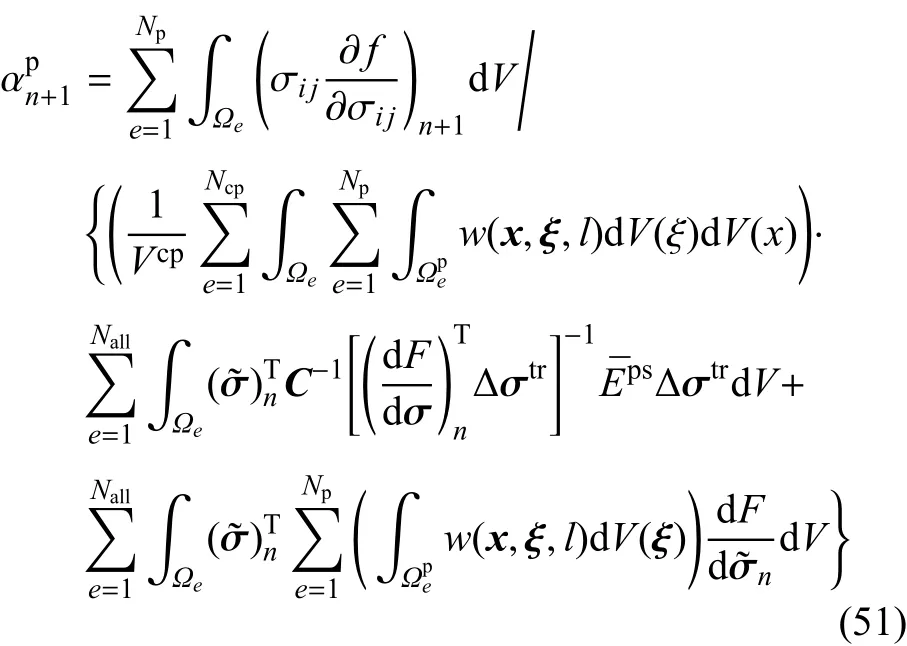
将式(49)~式(51)代入式(44)~式(48),可以得到非局部状态分量的增量并对全部非局部状态和局部状态的分量进行更新.系数re和弹性应力增量∆n+1可以依据式(16)和式(15)得到.式(16)和式(15)的离散形式可以分别写为

其中试应力增量∆σtr可以通过对边界∂u1Ω施加位移增量∆∂u1Ω,然后通过弹性分析得到.应力增量∆n+1和全应力n需要代入非局部屈服条件式(4)以检查其是否满足屈服条件.如果条件
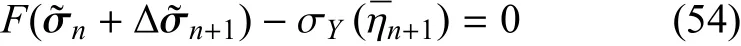

相应的等效节点力为
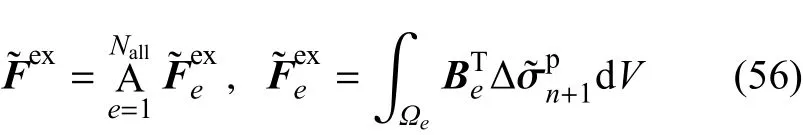
其中,“A”代表有限元中的组合算子(详见文献[32]).单元刚度矩阵Ke的计算和及整体刚度矩阵K的形成可以通过常规方法得到

与塑性应变相应的等效位移可由下式得出

在这一过程中,自然边界∂u1Ω上没有约束,因为边界∂u1Ω上的反力在塑性流动过程中保持不变,而边界∂u0Ω上的位移保持为零.

以上算法总结于如下:
假定在第n级载荷(应变软化阶段)已得到边界∂u1Ω上的状态分量
(1)在边界∂u1Ω上施加增量位移∆n+1然后计算弹性试应力∆σtr
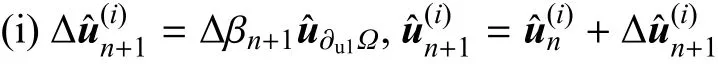
(2)计算外力功的变化∆Wn+1
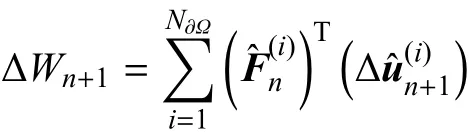
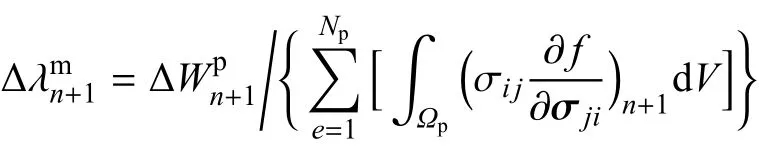
(5)计算非局部塑性乘子和塑性应变增量
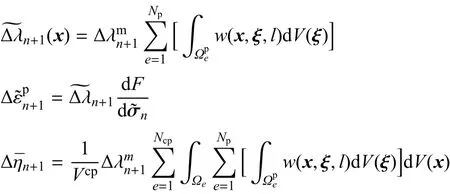
(6)计算系数re,弹性应力和应变增量∆n+1和
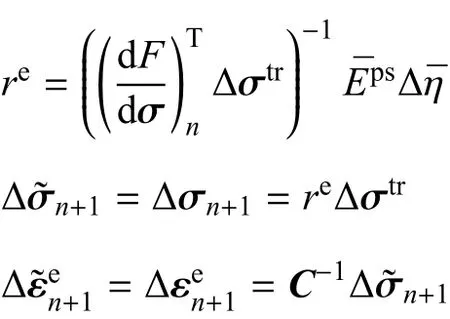
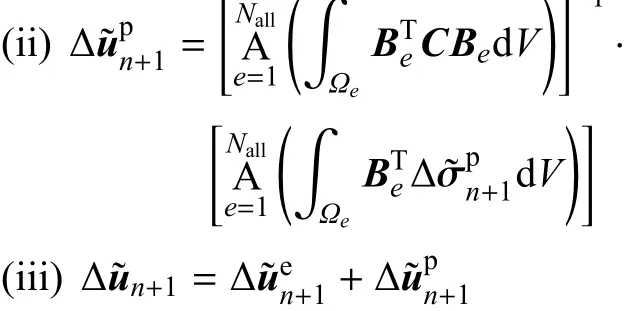
(8)更新局部和非局部状态空间的分量
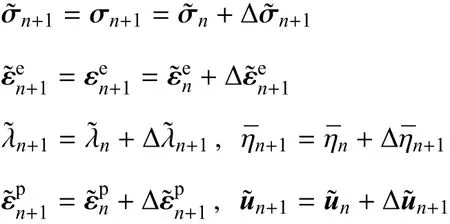
4 算例
4.1 一维应变局部化的数值解
应用本文提出的数值解法对文献[29]中的一维拉杆算例进行了有限元分析.拉杆几何形状和边界条件参见文献[29]中图1.除了内尺度以外的其他材料参数均和文献[29]中的参数相同.此处材料内尺度取l=6.26mm作为参照内尺度,对应于文献[26]中Nilsson的模型中具有不同定义的材料内尺度15.7mm.并以l=4.31mm,l=2.35mm作为对比,以考察不同的材料内尺度对局部化区域尺寸的影响.有限元网格采用常应变两节点单元,每个单元有两个高斯积分点.共采用的单元数量分别为5,11,41,101四种网格进行计算,数值计算结果示于图1~图5中.图1和图2表明,随着网格越来越细小,应变局部化过程中的塑性应变分布、局部化区域的尺寸、以及载荷位移曲线都稳定地收敛到解析解.图3表明,随着拉杆端部位移的增加,分布在局部化区域内的塑性应变也增加,局部化区域虽然有所扩展,但大体上不变.对于l=6.26mm的情况,局部化区域尺寸为Lcp=6l=6×6.26mm=37.56mm.图4和图5给出了塑性应变分布和载荷--位移曲线随着不同材料内尺度l的变化情况.从这两图可以看出,随着l的减小,塑性应变越来越集中于更小的区域.当l→0,本文的非局部方法得到的数值结果接近于局部塑性理论得到的解.这与文献[29]得到的结论是一致的.
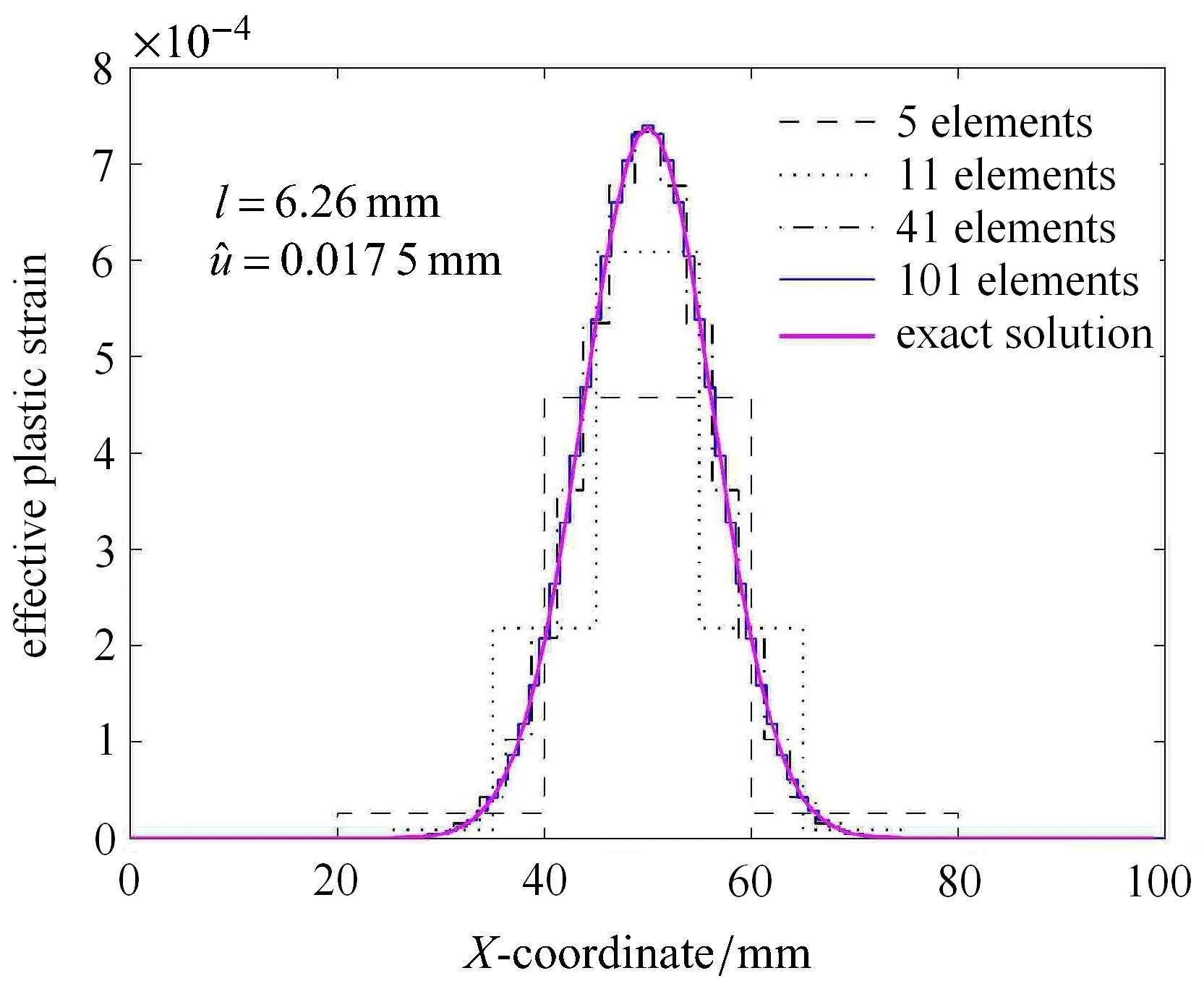
图1 一维拉杆在不同有限元网格下的塑性应变分布Fig.1 Plastic strain distributionsalong the axisof thebarunder tension for di ff erentmeshes

图2一维拉杆在不同有限元网格下的载荷--位移曲线Fig.2 Load-displacementcurvesof thebarunder tensionw ith strain softening for di ff erentmeshes
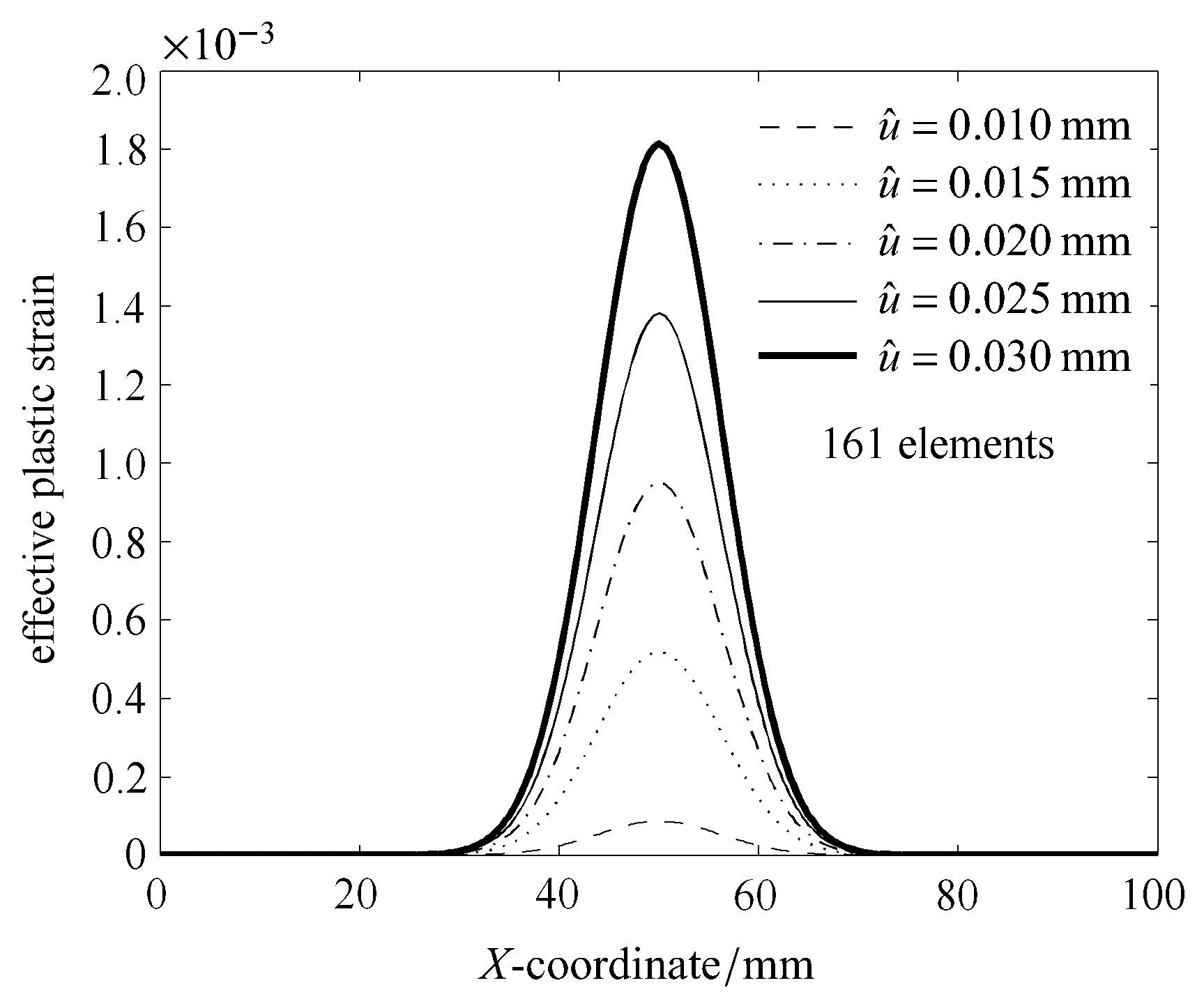
图3 一维拉杆中塑性应变随着端部位移增大的发展Fig.3 Developmentof plastic strainsalong theaxisof thebarw ith increased end displacement
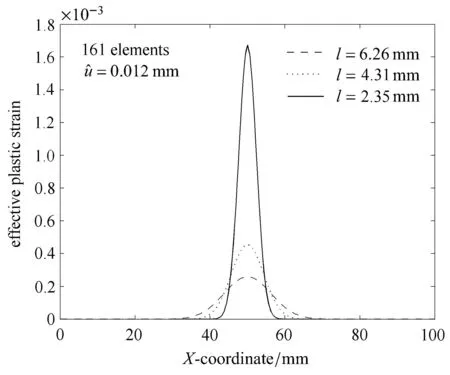
图4 一维拉杆内塑性应变随着不同材料内尺度的变化Fig.4 Plastic strain distributionsalong theaxisof thebar for di ff erent internal length scales
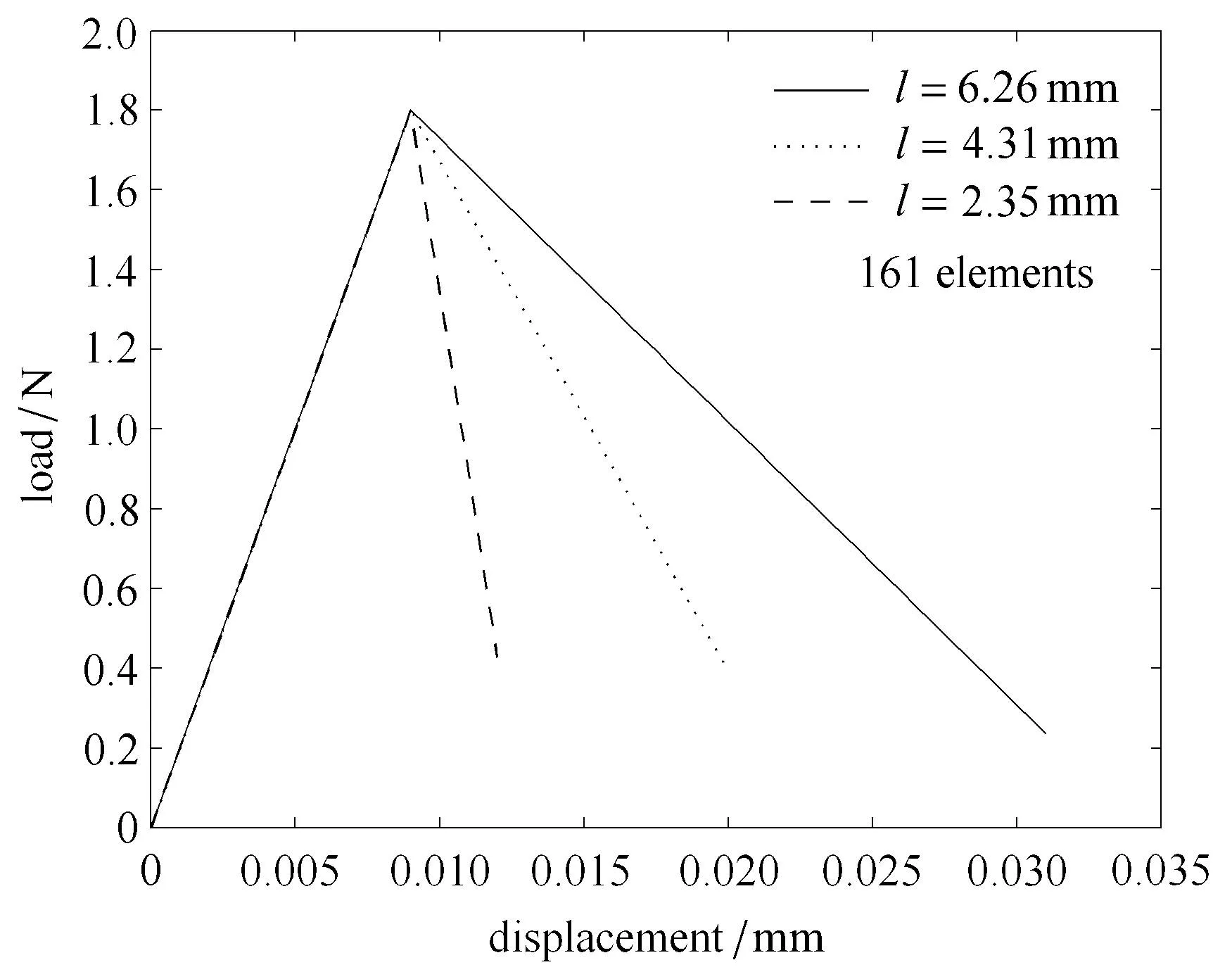
图5 一维拉杆在不同的材料内尺度下的载荷--位移曲线Fig.5 Load-displacementcurvesof thebarw ith di ff erentinternal length scales
4.2 二维剪切带局部化的数值解
4.2.1 平面应变加载试件
一个处于平面应变加载状态的试件的几何和加载条件见图6.试件尺寸为60mm×120mm,其底面放置在水平的刚性平面上,两个侧面受水平方向的刚性约束,顶面保持水平并通过一个刚性压板缓慢地施加可控的位移.试验过程中,垂直于XY平面的方向的变形保持为零.材料特性参数如下:E=11920MPa;泊松比v=0.2;σY0=100MPa;ps=-0.1E=-1192MPa.假定线性应变软化并且采用von M ises屈服准则.为了与一维算例一致,采用二维高斯型权函数如下
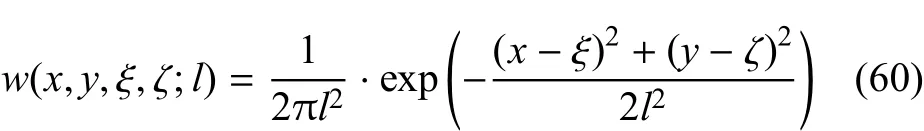

图6 平面应变加载试验的试件和加载方式Fig.6 Geometry and loading condition of the specimen under plane strain test
为了触发应变局部化,在试件左下角指定尺寸7.5mm×7.5mm的方形区域为弱区域,它的屈服强度为并采用了3个不同的材料内尺度l=6.26mm,l=3.13mm和l=1.565mm以考察剪切带局部化受内尺度影响的程度.有限元采用八节点等参元,形函数在单元之间是C0连续.每个单元内采用2×2高斯积分点.应用3种不同的有限元网格,即128个单元(粗),512个单元(中等),和2048个单元(细).这些网格数量都是8×16网格的整数倍,每种网格的弱区域尺寸都相同.
为了确定应变软化过程中特征塑性区域Vcp的大小,在应变局部化开始之后,首先在域Ωp中所有屈服单元的积分点的内变量中选出最大值

然后,对每一屈服单元,如果满足
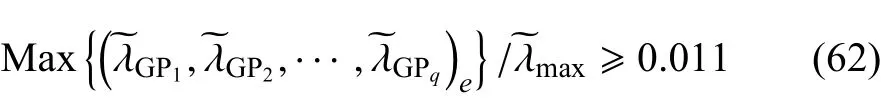
那么它就会被包含到Vcp中,否则从Vcp除去.这将保证99.7%的塑性变形包含在Vcp中.
计算结果见图7~图10.对于内尺度l=6.26mm,3种不同网格的变形情况示于图7.变形的网格清晰地显示了应变软化过程中变形集中在一个带状区域(剪切带).剪切带的宽度和方向基本上没有随着网格的不同而改变,这在图8的等效塑性应变分布中也可以看出.剪切带的方向与X轴成近似45°.注意到,通过非局部塑性模型得到的剪切带以外区域的变形与基于梯度塑性模型得到的结果略有不同(详见文献[18]).这是因为非局部模型的高斯型权函数是渐进趋于零的,而且在弹塑性边界上没有(不需要)指定边界条件.图9表明随着网格的细化,载荷--位移曲线稳定地收敛.采用精细网格得到的峰值后曲线比采用粗网格得到的要陡.
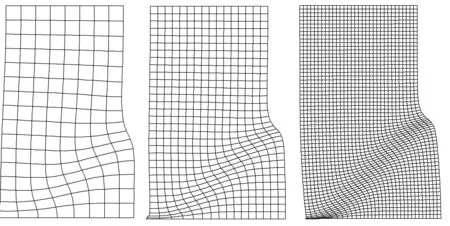
图7 3种有限元网格的变形(l=6.26mm,ˆu=3mm)Fig.7 Deformation patterns for three di ff erentmeshes(l=6.26mm,ˆu=3mm)
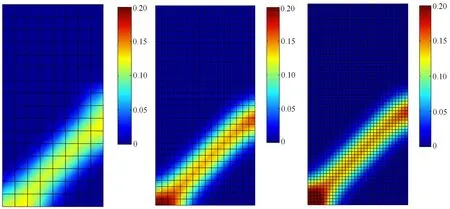
图8 3种有限元网格的等效塑性应变分布Fig.8 Contour plotof theequivalentplastic strains for three di ff erentmeshes(l=6.26mm,=3mm)
图10 给出了在边界位移ˆu=1.15mm作用下,3种不同的内尺度对应的等效塑性应变分布.从图中可看出,剪切带的宽度随着内尺度的减小而明显减小,对应于3个内尺度l=6.26mm,3.13mm和1.565mm的3个剪切带的宽度分别是大约38mm,19mm,9mm,大体上等于6l.这与文献[29]中的式(58)预测的值是一致的.图12表明随着内尺度的减小,峰值后下降段曲线的向下坡度增加.当内尺度变得很小时,如l=1.565mm,峰值后曲线就会变得非常陡.这些结果与一维应变局部化的结果是一致的,并且也和梯度塑性模型预测的结果相符[16,18].

图9 3种不同网格的载荷--位移曲线Fig.9 Load-displacementcurves for three di ff erentmeshes
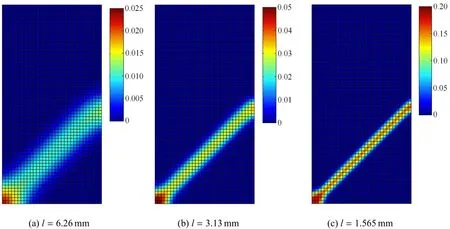
图10 不同材料内尺度对应的等效塑性应变分布(ˆu=1.15mm)Fig.10 Contour plotof theequivalentplastic strains for three di ff erent internal length scale(ˆu=1.15mm)
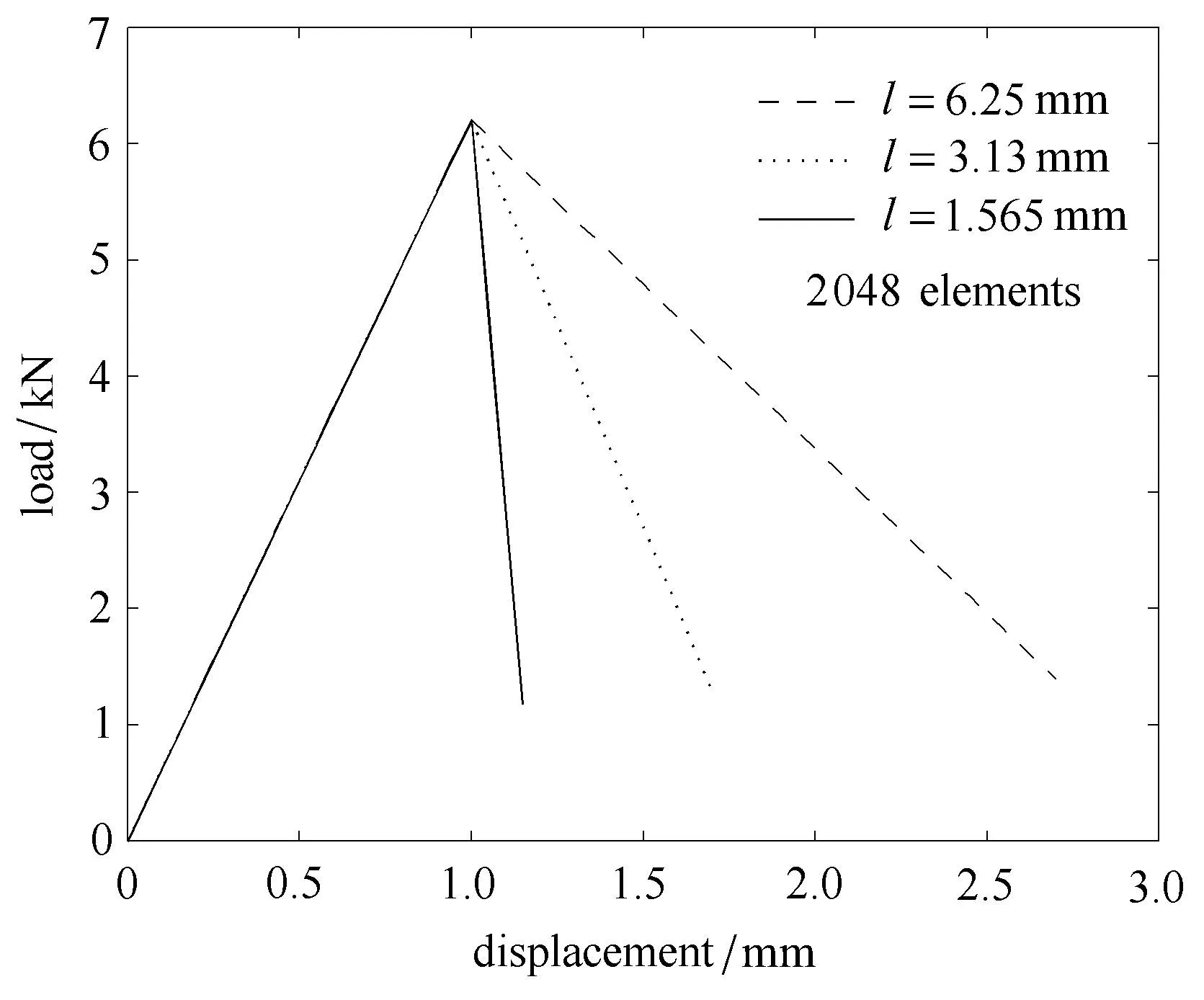
图11 不同材料内尺度对应的载荷--位移曲线Fig.11 Load-displacementcurves for di ff erentinternal length scales
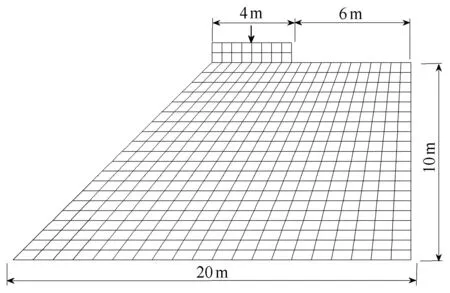
图12 边坡的几何尺寸和有限元网格Fig.12 Geometry and finit elementmesh of an embankment
4.2.2 边坡稳定性
为了进一步验证本文提出的模型,考虑图13所示的边坡失稳问题.边坡上有一基础,其刚度比边坡材料大很多,可视为是刚性的.这一算例曾经由Borja和Regueiro[33]用来验证他们提出的强不连续局部化模型.本文采用下列材料特性参数:E=10MPa;v=0.4;σY0=100 kPa;¯Eps=-0.1E=-1.0MPa;容重γ=16kN/m2.仍采用von M ises屈服准则和高斯权函数以及线性软化假定.有限元网格采用416个八节点等参元.为了使剪切带的厚度大于网格尺寸,材料内尺度取为l=150mm.计算得到边坡失稳后的网格变形和载荷--位移曲线分别如图13和14所示.由图13中可见,采用本文模型得到的剪切带区域的网格变形是平滑的,而采用一般非局部塑性模型得到的剪切带是不光滑的,且厚度大约和一个单元的尺寸相近.由图14也可看出,用本文模型得到的载荷位移曲线在越过峰值点后平滑地逐渐下降,而采用一般非局部模型得到的曲线在越过峰值点后以很陡的斜率突然下降,后者是数值模拟结果具有网格相关性的典型特征.

图13 边坡失稳后的变形Fig.13 Deformedmesh of the slope

图14 边坡失稳过程中的载荷--位移曲线Fig.14 Load-displacementcurves for the slope
4.2.3 煤岩的平面应变加载试验
为了与试验结果对比以验证数值结果的可靠性,用本文模型对文献[34]中的煤岩试件在平面应变条件下的加载试验进行了有限元分析.材料参数为:E=4.0GPa;v=0.19;黏聚系数c=16.83MPa;内摩擦角φ=25°;ps=-400.0MPa.采用Drucker-Prager屈服准则和关联流动法则,并仍用高斯权函数以及线性软化的假定.由于前述算例已经表明,采用本文提出的模型可得到与网格无关的结果,所以将试件划分为300个单元以节约计算时间.材料内尺假定为l=0.3mm.图15是煤岩试件破坏形态的试验结果和数值模拟结果的比较;图16是载荷位移曲线的试验和计算结果的比较.由于本试件在加载时没有侧向的约束载荷,因此试验时没有得到载荷--位移曲线的明显下降段.但是由图15和图16可见,计算和试验得到的剪切带位置和倾角基本相同,试验和计算得到的载荷--位移曲线的相当接近的.由于试验结果没有给出剪切带的厚度,所以无法推算出材料内尺度,用于数值模拟所用的材料内尺度是根据单元最小尺寸假定的.因此,计算得到的剪切带厚度只能是大体的尺寸.值得提到的是,剪切带厚度是试件断裂之前塑性变形集中的区域,它的精确测量较为困难,尤其对于尺寸较小的试件[3435].
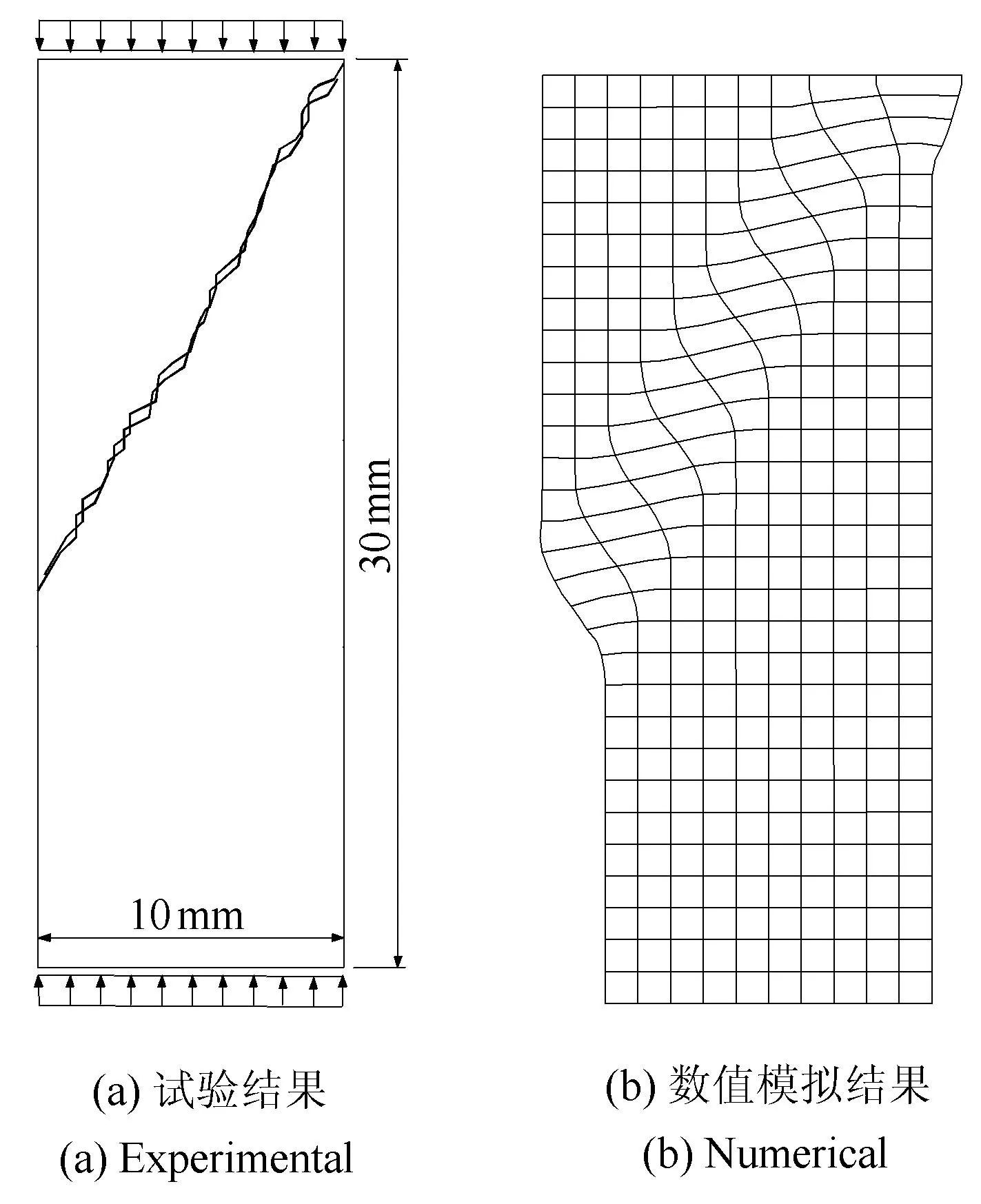
图15 煤岩平面应变加载破坏形态Fig.15 Failure pattern of the coalspecimen under plan strain compression test

图16 煤岩平面应变试验的载荷--位移曲线Fig.16 Load-displacementcurves for the coalspecimen
5 结论
本文以非局部塑性理论和状态空间理论为基础,通过局部和非局部两个状态空间能量的等效原理,提出了一种对应变局部化进行数值模拟的新方法.本文所提出的方法可以克服经典的局部塑性理论和一般非局部塑形理论导致的网格相关性问题,从而得到应变局部化问题的客观解.本文导出了二维问题的一般列式,并给出了有限元算法.一维和二维问题的有限元算例表明,应用本文的模型和算法得到的塑性应变分布和载荷--位移曲线随着单元网格尺寸的细化而稳定地收敛.这说明,用本文的方法可得到与网格无关的结果.由于采用了两个状态空间塑性耗散能的等效,因而应变局部化过程中能量的耗散总是大于零.算例分析还表明,剪切带的厚度依赖于材料内尺度,当材料内尺度趋近于零时,本文方法的结果将退化为经典的局部塑性理论的结果.
与梯度塑性理论相比,在有限元分析中采用本文的模型和方法只需要位移场在单元之间具有C0连续性,不要求斜率的连续性,因此本文的算法容易嵌入到现有的有限元程序中而不需要做大的修改.对于大尺寸岩土结构的有限元分析,本文的方法易于在有限元程序中实现.
本文仅采用了von M ises和Drucker-Prager屈服准则求解各向同性应变软化导致的应变局部化.将来进一步的研究需要考虑应用较为复杂的屈服准则,如Mohr-Coulomb准则以及帽盖模型(cap model),并采用非关联流动法则和非线性软化模型.随动软化和各向异性软化以及大变形情况下如何应用本文的方法也有待研究.
致谢本文部分二维计算程序在中国科学院超级计算环境(ScGrid)上运行并获得结果,特此致谢!
1黄茂松.土体稳定与承载特性的分析方法.岩土工程学报,2016,38(1):1-34(Huang Maosong.Analysismethods for stability and bearing capacity of soils.Chinese Journal ofGeotechnical Engineering,2016,38(1):1-34(in Chinese))
2钱建固,吕玺琳,黄茂松.平面应变状态下土体的软化特性与本构模拟.岩土力学,2009,30(3):617-622(Qian Jiangu,L¨u Xilin,Huang Maosong.Softening characteristics of soilsand constitutive modeling under plane strain condition.Rock and SoilMechanics,2009,30(3):617-622(in Chinese))
3徐连民,王天竹,祁德庆等.岩土中的剪切带局部化问题研究:回顾与展望.力学季刊,2004,25(4):484-489(Xu Lianmin,Wang Tianzhu,QiDeqing,etal.Study on geotechnicalshear band localization:retrospectand prospect.Chinese Quarterly ofMechanics,2004,25(4):484-489(in Chinese))
4张启辉,赵锡宏.粘性土局部化剪切带变形的机理研究.岩土力学,2002,23(1):31-35(ZhangQihui,Zhao Xihong.Study onmechanism of localized shearband formation in clay.Rock and SoilMechanics,2002,23(1):31-35(in Chinese))
5王杰,李世海,张青波.基于单元破裂的岩石裂纹扩展模拟方法.力学学报,2015,47(1):105-118(Wang Jie,LiSihai,ZhangQingbo.Simulation of crack propagation of rock based on splitting elements.Chinese JournalofTheoreticaland Applied Mechanics,2015,47(1):105-118(in Chinese))
6李宏儒,胡再强,冯飞等.结构性黄土二元介质本构模型在局部化剪切带中的应用.岩土力学,2012,33(9):2803-2844(LiHongru,Hu Zaiqiang,Feng Fei,etal.Application ofstructural loessbinarymedium model to localization shearband.Rockand SoilMechanics,2012,33(9):2803-2844(in Chinese))
7黄茂松,贾苍琴,钱建固.岩土材料应变局部化的有限元分析方法.计算力学学报,2007,24(4):465-471(Huang Maosong,Jia Cangqin,Qian Jiangu.Strain localization problems in geomaterials using finit elements.Chinese Journal ofComputational Mechanics,2007,24(4):465-471(in Chinese))
8邵龙潭,刘港,郭晓霞.三轴试样破坏后应变局部化影响的实验研究.岩土工程学报,2016,38(3):385-394(Shao Longtan,Liu Gang,Guo Xiaoxia.E ff ects of strain localization of triaxial samples in post-failure state.Chinese Journal ofRock Mechanics and Engineering,2016,38(3):385-394(in Chinese))
9李学丰,黄茂松,钱建固.基于非共轴理论的各向异性砂土应变局部化分析.工程力学,2014,31(3):205-246(LiXuefeng,Huang Maosong,Qian Jiangu.Strain localization analysis of anisotropic sands based on non-coaxial theory.Engineering Mechanics,2014,31(3):205-246(in Chinese))
10王水林,郑宏,刘泉声等.应变软化岩体分析原理及其应用,岩土力学,2014,35(3):609-630(Wang Shuilin,Zheng Hong,Liu Quansheng,etal.Principleofanalysisof strain-softening rockmass and itsapplication.Rock and SoilMechanics,2014,35(3):609-630(in Chinese))
11 Read HE,Hegemier GA.Strain softening of rock,soil and concrete—a review article.Mechanics and Materials,1984,3(3):271-294
12 Vardoulakis I.Shear band inclination and shearmodulus of sand in biaxial test.International Journal for Numerical and Analytical Methods in Geomechanics,1980,4(2):103-119
13 Jir´asek M,Ba˘zant ZP.Inelastic analysis of structures.Chichester,England:JohnWiley&Sons,2002
14 Pietruszczak ST,M r´oz Z.Finite element analysis of deformation of strain-softening materials.International Journal for Numerical Methods in Engineering,1981,17(3):327-334
15 OrtizM,Leroy Y,Needleman A.A finit elementmethod for localized failure analysis.ComputerMethods in Applied Mechanicsand Engineering,1987,61(2):189-214
16 de Borst R,Sluys LJ,M¨uhlhaus H-B,et al.Fundamental issues in finit elementanalyses of localization of deformation.Engineering Computations,1993,10(2):99-121
17 Simo JC.Strain softening and dissipation:a unificatio of approaches//Mazars J,Ba˘zant JP,eds.Cracking and Damage:strain localization and size e ff ect.London and New York:Elsevier Applied Science,1988:440-461
18 de Borst R,M¨uhlhaus H-B.Gradient-dependent plasticity:formulation and algorithm aspects.International Journal for Numerical Methods in Engineering,1992,35(3):521-539
19 Luzio GD,Ba˘zant ZP.Spectral analysis of localization in nonlocaland over-nonlocalmaterialsw ith softening plasticity ordamage.International JournalofSolidsand Structures,2005,42(23):6071-6100
20 Vermeer PA,BrinkgreveRBJ.A new e ff ectivenon-localstrainmeasure for softening plasticity//Chambon V,Desrues J,Vardoulakis I,eds.Localisation and Bifurcation Theory for Soilsand Rocks.Rotterdam,Netherland:A.A.Balkema,1994
21 Str¨omberg L,Ristinmaa M.FE-formulation of a nonlocalplasticity theory.ComputerMethods in Applied Mechanicsand Engineering,1996,136(1-2):127-144
22 L¨u XL,Bardet J-P,Huang MS.Numerical solutions of strain localization w ith nonlocal softening plasticity.ComputerMethods in Applied Mechanicsand Engineering,2009,198(47):3702-3711
23 L¨u XL,Bardet J-P,Huang MS.Spectralanalysisof nonlocal regularization in two-dimensional finit elementmodels.InternationalJournal of Numerical and Analytical Methods in Geomechanics,2012,36(2):219-235
24 Ba˘zant ZP,Lin F-B.Nonlocalsmeared crackingmodel for concrete fracture.Journal ofstructural Engineering,1988,114(11):2493-2510
25 Eringen AC.Nonlocal Continuum Field Theories.New York:Springer-Verlag,2002
26 Nilsson C.Nonlocal strain softening bar revisited.International JournalofSolidsand Structures,1997,34(34):4399-4419
27 Borino G,Fuschi P,Polizzotto C.A thermodynamic approach to nonlocalplasticity and related variationalprinciples.JournalofApplied Mechanics,1999,66(4):952-963
28 de Sciarra FM.A general theory for nonlocal softening plasticity of integral-type.International Journal of Plasticity,2008,24(8):1411-1439
29武守信,魏吉瑞,杨舒蔚.基于能量等效原理的应变局部化分析I:一维解析解.力学学报,2017,49(3):(Wu Shouxin,WeIJirui,Yang Shuwei.Analysisof strain localization by energy equivalence between local and nonlocal state spaces-part I:one-dimensional analyticalsolution.Chinese JournalofTheoreticaland Applied Mechanics,2017,49(3):(in Chinese))
30冯春,李世海,刘晓宇.基于颗粒离散元法的连接键应变软化模型及其应用.力学学报,2016,48(1):76-85(Feng Chun,LiShihai,Liu Xiaoyu.Particle-dem based linked bar strain softening model and itsapplication.Chinese JournalofTheoreticaland Applied Mechanics,2016,48(1):76-85(in Chinese))
31万征,姚仰平,孟达.复杂加载下混凝土的弹塑性本构模型.力学学报,2016,48(5):1159-1171(Wan Zheng,Yao Yangping,Meng Da.An elastoplastic constitutivemodel of concrete under complicated load.Chinese JournalofTheoreticaland Applied Mechanics,2016,48(5):1159-1171(in Chinese))
32 Simo JC,Hughes TJR.Computational Inelasticity.New York:Springer-Verlag,1998
33 Regueiro RA,Borja RI.A finit elementmodel of localized deformation in frictionalmaterials takingastrong discontinuity approach.Finite Elements in Analysisand Design,1999,33:283-315
34 Yum lu M,Ozbay MU.A study of the behavior of brittle rocks under plan strain and triaxial loading condition.International Journal ofRockMechanicsand M ining Science&Geomechanics Abstracts,1995,32(7):725-733
35韩铁林,师俊平,陈蕴生等.轴、侧向同卸荷下砂岩力学特性影响的试验研究.力学学报,2016,48(3):936-943(Han Tielin,Shi Junping,Chen Yunsheng,etal.Experimental study onmechanics characteristicsofsandstoneunderaxialunloadingand radialunloading path.Chinese Journal of Theoretical and Applied Mechanics,2016,48(3):936-943(in Chinese))
ANALYSISOFSTRAIN LOCALIZATION BY ENERGY EQUIVALENCE:II.FINITE ELEMENT SOLUTION1)
Wu Shouxin∗,†,2)Wei Jirui∗,†Yang Shuwei∗,†∗
(DepartmentofBridge Engineering,SchoolofCivil Engineering,Southwest Jiaotong University,Chengdu 610031,China)†(Key Laboratory ofTransportation TunnelEngineering ofMinistry ofEducation,Chengdu 610031,China)
Founded on the nonlocalplasticity and the state space theories,anew approach isproposed to fin themeshindependent solution of the strain localization problems by equating the rates of plastic energy dissipation in the local and nonlocal state spaces.Follow ing the previous paper by the authors,general formulas are developed for the solution of the nonlocal internal variables in the two-andmore than two-dimensional problems.A stress updating algorithm is proposed to integrate the rate form constitutive equations in the finit elementcontext.To verify the proposed approach,a one-dimensionalmodel problem and three two-dimensional plane strain problems are solved numerically by the finit elementmethod.Numerical results show that the plastic strain distributions and the load-displacement curves stablyconvergewithrefinemen of the finit elementmesh.The sizeof the localization zone dependsonly on the internal length scaleand is insensitive to themesh size.For the one-dimensionalproblem,numericalsolutions converge to the analytical ones.For the two-dimensionalproblems,although no analyticalsolutionsareavailable,thenumericalsolutions converge toward the unique ones.Thew idth and the inclination are almost not changed as themesh size is reduced.Also,the distribution of the plastic strainsand the deformation patternsare smooth in the entire domain.A slope stability problem and a plane strain test of a coal specimen are also solved numerically to demonstrate the robustness of the proposed approach.It iswell shown that the proposed approach can overcome the drawbacks of the classical continuum theory and lead to physicallymeaningful,mesh-independentsolution of strain softening problems.Because only C0continuity isneeded between elementboundaries,the proposed approach is easy to be incorporated into the existing finit element codew ithoutsubstantialmodification
strain localization,nonlocalplasticity,internal length scale,mesh-dependence,finit element
O344.3,TU501
A
10.6052/0459-1879-16-330
2016-11-14收稿,2017-03-20录用,2017-03-21网络版发表.
1)教育部留学回国人员科研启动基金(201250300)和西南交通大学土木工程学院基础研究创新计划基金资助项目.
2)武守信,副教授,博士,主要研究方向:桥梁和岩土结构的有限元分析和本构关系.E-mail:swu@home.sw jtu.edu.cn
武守信,魏吉瑞,杨舒蔚.基于能量等效原理的应变局部化分析:II.有限元解法.力学学报,2017,49(4):880-893 Wu Shouxin,WeiJirui,Yang Shuwei.Analysisofstrain localization by energy equivalence:II.Finiteelementsolution.Chinese Journal ofTheoreticaland Applied Mechanics,2017,49(4):880-893

