一种分类数据聚类算法及其高效并行实现

丁祥武 谭 佳 王 梅

(东华大学计算机科学技术学院 上海 201620)



一种分类数据聚类算法及其高效并行实现

丁祥武 谭 佳 王 梅

(东华大学计算机科学技术学院 上海 201620)

针对大规模、高维、稀疏的分类数据聚类，CLOPE算法相比于传统的聚类算法在聚类质量及运行速度上都有很大的提升。然而CLOPE算法存在聚类的质量不稳定、没有区分每维属性对聚类的贡献度、需要预先指定排斥因子r等问题。为此，提出基于随机顺序迭代和属性加权的分类数据聚类算法(RW-CLOPE)。该算法利用“洗牌”模型对原始数据进行随机排序以排除数据输入顺序对聚类质量的影响。同时，根据信息熵计算各个属性的权重，以区别每维属性对聚类的贡献度，极大地提升了数据聚类的质量。最后，在高效的集群平台Spark上，实现了RW-CLOPE算法。在三个真实数据集上的实验结果表明：在数据集乱序后的份数相同时，RW-CLOPE算法比p-CLOPE算法取得更好的聚类质量。对蘑菇数据集，当CLOPE算法取得最优聚类结果时，RW-CLOPE比CLOPE取得高68%的收益值，比p-CLOPE取得高25%的收益值；针对大量数据，基于Spark的RW-CLOPE算法比基于Hadoop的p-CLOPE算法执行时间更短；计算资源充足时，随机顺序的数据集份数越多，执行时间的提升越明显。

分类数据 CLOPE p-CLOPE RW-CLOPE Spark

0 引 言

目前，针对数值型数据的聚类算法虽然在不断取得突破，但并不适合处理分类数据的聚类。分类数据在零售业、电子商务、医疗诊断、生物信息学等领域都有大量的应用。与数值型数据相比，分类数据的属性值取自一个有限的离散的符号集合，如DNA序列数据以4种不同的符号A、T、G和C编码，因此分类数据间的相似度量的定义更加困难。现有的数值型数据的聚类方法和工具难以直接应用于分类数据聚类，因此，研究分类数据的聚类算法具有重要的学术意义和应用前景。

在现有的分类数据聚类算法中，CLOPE[1]算法以其实现思想简单、收敛速度快、聚类质量优等特点受到学术界的关注。自2004年由Yang等提出后，CLOPE算法被应用于数据流聚类、日志分析、入侵检测等多个领域[2-4]，成为了当前主流的分类数据聚类算法之一。CLOPE算法根据簇直方图的高宽比来表示这个簇内记录的重叠程度并提出一个全局聚类指标用来评估聚簇的质量。与典型的分类数据聚类算法ROCK[5]、LargeItem[6]相比，CLOPE在单机上对同一份数据集进行聚类的运行速度快于LargeItem和ROCK，聚类质量优于LargeItem。尽管CLOPE算法的聚类质量及运行速度优于传统聚类算法，但还存在一些缺陷，如需要预先指定排斥因子r、聚类的质量不稳定、 没有区分各属性对聚类的贡献度差异等。聚类质量上的不足主要表现在两个方面：1) 对内部排列顺序不同的数据，CLOPE算法对应的聚类质量也不同。2) 当CLOPE用于非交易数据聚类时，忽视了属性维权值对聚类质量的影响。针对这些问题，已经有学者提出了CLOPE的一些改进算法，如Li等[7]提出了一种修正的划分模糊度，来实现对算法中排斥因子r的自动优选。丁祥武等[8]基于MapReduce平台，提出了等分划分再排列的思想，对不同输入顺序的数据进行聚类，再从中选出最优聚类，一定程度上降低了数据集顺序对聚类质量的影响。但是，上述的改进工作存在如下不足：在聚类质量的稳定性上，p-CLOPE算法对数据集的打乱程度依赖于划分后的块数。当块数较少时，数据的打乱程度低，无法取得最优的聚类结果；当划分的块数较大时，数据虽然打乱程度高，但花费了巨大的时间开销。更为重要的是FUZZY CLOPE与p-CLOPE算法对非交易数据集进行聚类时，默认数据集中每一维的属性对聚类的贡献程度相同。然而现有研究表明，每一维属性对聚类的贡献程度是不一致的，给每一维属性设置不合适的权值将很大程度上影响算法的聚类质量。

本文提出了一种基于随机顺序迭代和属性加权的新分类数据聚类方法RW-CLOPE。该方法具体如下：首先利用“洗牌”模型，将待聚类的数据集进行随机化打乱，几乎完全克服了CLOPE算法的聚类质量受数据集内部排列顺序的影响。在此基础上，RW-CLOPE算法根据数据的信息熵，计算每一维属性相应的权值以区分其对聚类的贡献度。在实现上，利用Spark平台的特性，设计了基于Spark的算法，改善了p-CLOPE算法的扩展性不足问题。在3个真实数据集上的实验结果表明，与现有算法相比，该算法在聚类质量和聚类效率上有明显的提升。

1 相关工作

依据是否为聚类过程定义显式的目标优化函数，现有的分类数据聚类方法可以划分为两类。以层次聚类为代表的第1类方法，其目的是构造层次聚类树，因而没有必要显式地定义聚类目标函数，其代表性算法包括凝聚性算法ROCK和分裂型算法DHCC等[9]。此类算法具有较高的算法复杂度，通常达到O(N2logN)。第2类算法的主要代表是基于分割熵或频度统计信息定义聚类目标函数，然后定义用于优化目标函数的聚类搜索算法，其代表性算法包括基于熵的分类数据聚类算法[10]EBC(entropy-based categorical clustering)。该类算法通常使用蒙特卡罗抽样法[11]实现聚类优化，具体实现为：随机选择一个对象，将其移动到另一个簇，使得移动之后的划分具有更高的聚类质量(优化目标函数值)，重复这个过程直到目标函数值不再改变为止。因此，此类算法通常需通过大量的迭代来完成聚类。

依据聚类方式，现有分类数据的聚类算法可分为基于划分的聚类算法和基于层次的聚类。1998年Huang等对k-means算法进行扩展，提出了针对分类数据的k-modes聚类算法[12]。该算法对k-means算法进行了3点扩展：引入了针对分类数据的相似性度量(简单的0-1匹配)；使用modes代替means；在聚类的过程中使用基于频度的方法修正modes，以使得聚类代价最小化。但是该算法经过有限次迭代后仅能收敛于局部最优值，其次，聚类结果依赖于初始的modes的选择且modes不具有唯一性。1999年Huang等对Fuzzy k-means进行扩展，提出了针对分类数据的Fuzzy k-modes算法[13]。该算法使每个对象到所有的类有一个隶属程度，由隶属度构成的模糊划分矩阵不仅可以为用户提供更多的信息去决定最终的类，而且容易识别边界对象，但是Fuzzy k-modes与k-modes算法一样只能达到局部最优。为了寻找一个使模糊目标函数值最小且合适的模糊隶属矩阵，Gan等将Fuzzy k-modes算法作为一个优化问题去处理，提出的Gentic fuzzy -modes算法[14]在UCI的标准数据集上进行测试，实验结果表明，提出的算法在识别分类数据集中固有的类结构方面非常有效。1999年Guha等提出ROCK算法[5]，该算法的基本思想是首先对数据进行抽样，根据相似度阈值和共享近邻的概念构造一个凝聚的层次聚类算法，得到样本集的聚类后再对整个数据集进行聚类。ROCK算法将共享近邻数的全局信息作为评价数据点之间相关性的度量，而不是传统的基于两点间距离的局部度量函数。LargeItem算法[6]通过迭代优化一个全局评估函数来实现对大量分类数据的聚类，但其最小支持度θ和权重w很难确定。2004年Yang等提出了基于直方图的聚类算法CLOPE[1]，用簇直方图中的高宽比来表示这个簇内交易的重叠程度并提出一个全局聚类指标来评估聚簇的质量。

为了区别不同属性对聚类贡献程度的差异，从而提高聚类结果的质量，在数值聚类领域已经应用自动属性加权技术。这种技术赋予每个属性一个类依赖的权重并在聚类过程中给予优化，达到自动特征选择的目的。由此对现有分类数据聚类方法又可以分为两类：一类根据记录到modes的平均距离来赋予属性权重的方法，如：WKM算法[15]；另一类根据modes的频度来计算权重的方法，如DHCC算法等。在这类方法中，权值的设定只依赖于modes，没有考虑属性值的总体分布，因而导致属性在权重计算上的偏差，从而影响聚类结果的质量。譬如属性项Atrribute1(A,A,T,T,G)与属性项Atrribute2(T,A,C,G,G)在DHCC算法中将被赋予两个相同的权重，然而这个结果与事实不符。Atrribute2上属性值的分布比Atrribute1更密集，对簇的贡献度更大，所以二者对簇的贡献度应该给以区别。为了避免因为忽略属性的非modes信息而导致的权值计算偏差，另一种加权方法即根据分类属性值的总体分布情况赋予属性维的权值，如基于信息论中熵概念的加权方法[16]。

2 CLOPE算法

分类数据的聚类算法CLOPE以簇的直方图的高宽比作为全局评估函数(也称全局收益函数)，随着每个簇中记录重合度的增多，簇内的统计直方图的高宽比也逐渐增加。当簇集的统计直方图高宽比之和达到最大时，所对应的聚类结果被认为是最优的聚类。

定义1[1]分类数据集D是一组记录的集合{t1,t2,…,tn}。每条记录是一些属性项的集合{i1,i2,…,im}。聚类集合{C1,C2,…,Ck}是{t1,t2,…,tn}的一个划分，也就是说C1∪…∪Ck={t1,t2,…,tn}而且对任意1 ≤i≤k，满足Ci≠∅，且Ci∩Cj=∅。每一个Ci叫作一个簇，n、m、k分别表示交易的条数、属性项的个数和簇的个数。

给定一个簇C，可以找到这个簇中所有的不同属性项，一个属性项出现的频率表示有多少条记录包含这个属性项。用D(C)表示簇C中不同属性项的集合，用Occ(i,C)表示属性项i在簇C中出现的频率。这样可以画出簇C的直方图，用X轴表示属性项，用Y轴表示每个属性项出现的频率；一个簇C的直方图的面积S(C)和宽度W(C)为：

(1)

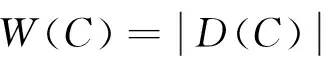
(2)

簇的高度定义为H(C)=S(C)/W(C)，全局评估函数为：

(3)

其中，排斥因子r是一个正实数，用来控制簇内记录的相似程度。当r较大时，簇内的记录必须有较多的公共项；相反，较小的r可用来对稀疏数据分组。通过调整排斥因子r的大小可以得到不同的簇个数，r越大，簇的个数越多。对于每个确定的r都可以找到一个划分C使得收益值Profit(C)最大。具体的算法如下：

算法1 CLOPE算法

/* 第1阶段：初始化 */

(1) while未到数据集尾部

(2) 读下一条记录;

(3) 据profit最大化原则，将t放入已有或新建的第i个簇中;

(4) 将写回数据集;

/* 第2阶段：迭代 */

(5)repeat

(6) moved = false;

(7) while未到数据集尾部

(8) 读一条记录;

(9) 据profit最大化原则，将t放入已有或新建的簇Cj中;

(10) ifCi≠Cj

(11) 将写回数据集;

(12) moved = true;

(13) endif;

(14) until moved=false;

CLOPE算法分为两个阶段：聚类生成阶段与聚类调整阶段。在第1阶段，CLOPE依据数据集中记录的顺序依次入簇，得到初始聚类划分。在第2阶段每一轮迭代中，将前一轮得到的聚类作为下一轮的输入，根据profit最大化的原则对前一轮得到的聚类进行调整，迭代结束时得到最终的聚类。由此，CLOPE算法得到的最终聚类依赖于第1阶段的聚类，而第1阶段的聚类，对同一数据集的不同输入顺序，得到的聚类是不同的。因此，CLOPE聚类的结果随输入顺序的不同而不同。这个特点，使得CLOPE算法的聚类质量存在很大的随机性。针对这个问题，p-CLOPE算法采用将待聚类数据集进行等分划分再排列的方式进行顺序打乱，然后对不同排列的数据进行CLOPE聚类，迭代的每一轮都选择上一轮的最优聚类作为输入并随机打乱数据块之间的顺序后进行调整。迭代结束后，选择最后一轮中的profit值最大的聚类作为最优聚类输出。p-CLOPE算法虽然能缓解数据输入顺序对聚类质量的影响，但是数据输入顺序按划分块打乱，打乱程度不够彻底，导致最后的聚类质量仍然受限即只能收敛于局部最优聚类。此外，在对非交易数据进行CLOPE聚类时，CLOPE算法默认每一维数据对聚类质量的贡献程度是相同的，没有考虑每一维数据对聚类贡献的差异性。

3 RW-CLOPE算法

3.1 对数据“洗牌”

经分析，CLOPE算法存在聚类质量随处理数据顺序不同而变动的问题，其后p-CLOPE算法虽然考虑到输入顺序对聚类质量的影响，但是p-CLOPE算法通过对划分块进行全排序以打乱数据顺序的粒度比较粗，使得无法得到最优聚类。为了解决这个问题，本文利用“洗牌”模型对数据按记录粒度进行随机化打乱。与等块划分再排列的打乱数据顺序的方法相比，本文提出的随机顺序方法更彻底地消除了顺序对聚类质量的影响。“洗牌”模型在处理每条记录时，都是随机从数据集中抽出一条记录，与剩余数据集中的最后一条记录交换，即把这个随机抽取的记录放到尚未处理数据集的最后一个位置。假设待聚类的数据集D为{x1,x2,x3,x4,x5},则执行一次“洗牌”模型的流程如图1所示。

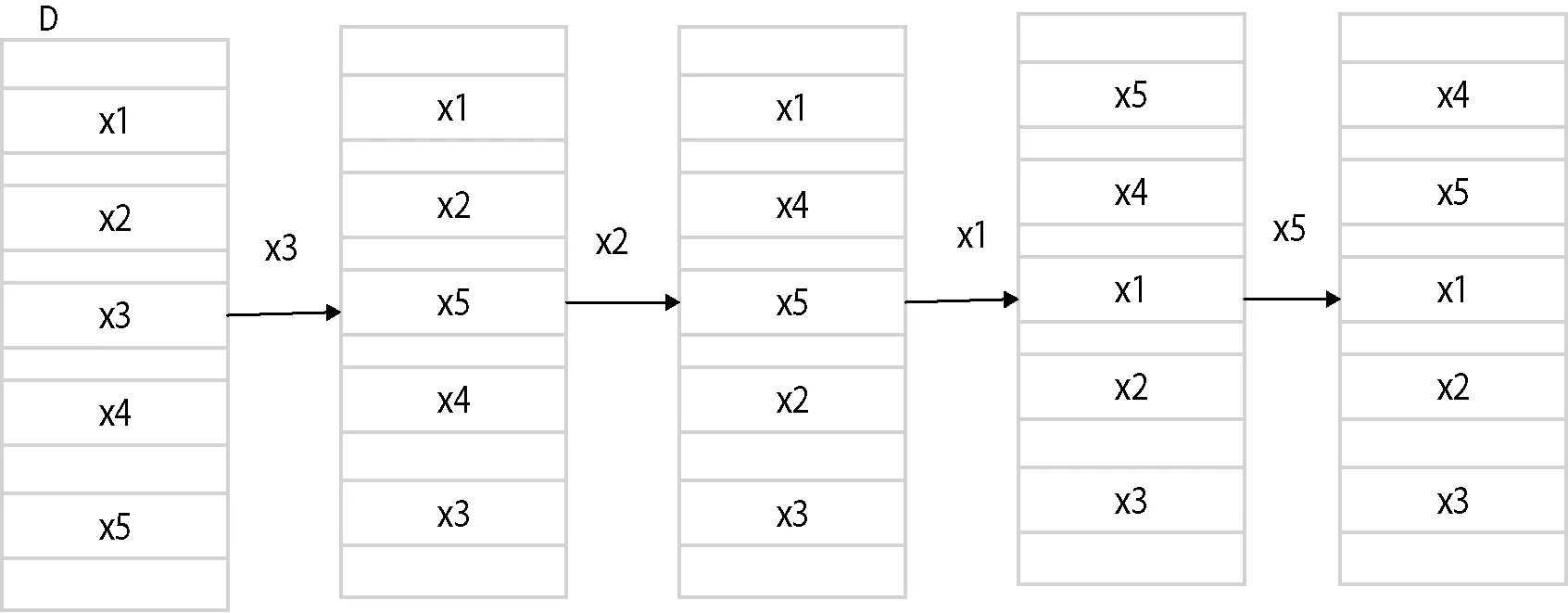
图1 “洗牌”模型流程图

对数据集D，执行一次“洗牌”模型的流程为：首先从数据集D中随机选择一条记录如x3与D中的最后一条记录x5交换，即将D中的最后输入的一条记录进行了随机化处理。然后从未被随机化的前4条记录{x1,x2,x5,x4}中随机抽取一条记录如x2与最后一条记录x4交换，再从{x1,x4,x5}中随机抽取如x1与x5交换。最后将x4与x5交换，此时D中所有的记录都进行了随机化处理，至此完成了一次“洗牌”操作。

在算法每一轮的迭代过程中，都对上一轮输出的最优聚类数据集，利用“洗牌”模型按记录粒度对数据集进行打乱。使RW-CLOPE能够从记录粒度的随机顺序集中选择最优的聚类，几乎完全排除了数据的输入顺序导致的聚类质量不稳定问题，从而在算法收敛时，能取得全局最优聚类。

3.2 属性维加权

在对非交易数据进行聚类时，CLOPE算法默认每个簇中的每一维数据对聚类贡献度一致，忽略了属性维对聚簇贡献度的差异性。如表1中的3个分类属性，易知它们的取值范围为{A,T,C,G}，在Attribute1中A和T出现的频率分别为0.4、0.4。在Attribute2中，A和T出现的频率分别为0.8、0.2。其中，Attribute2对簇C1的贡献度明显比Attribute1更大。因此，在聚类时，应该考虑到不同的属性维对聚类贡献度的差异性。表1由5个数据对象组成的分类数据簇。

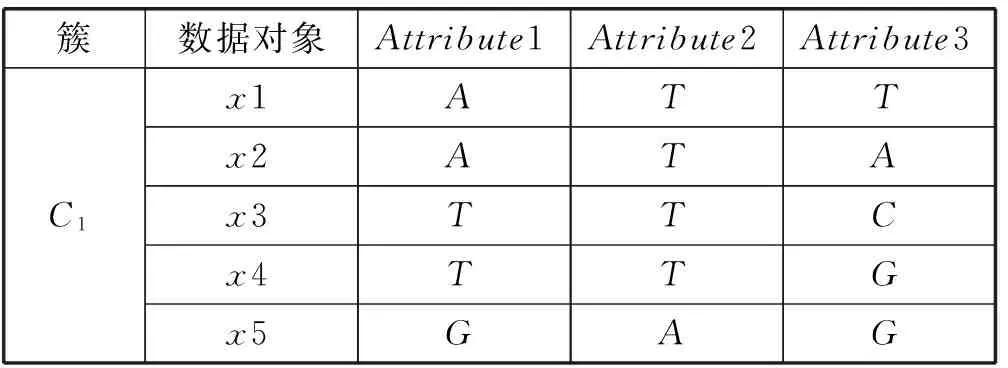
表1 分类数据簇

针对不同属性维对聚类贡献度不一致问题，本文依据属性维的信息熵给不同维度的数据赋与不同的权值。熵是信息论中描述消息携带平均信息量的度量，熵越大不确定性越大，其对应的权值越小，反之，熵越小不确定也越小，对应的权值就越大。

假设数据第j维的特征T是一个离散型随机变量T，其取值集合为T，则变量T的熵H(Tj)定义如下：

H(Tj)=-∑t∈Tp(t)lnp(t)

(4)

其中p(t)为属性值t在集合T中出现的概率：

(5)

根据特征T的信息熵，计算其对应的权值Wj:

(6)

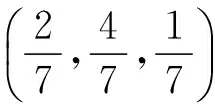
3.3 RW-CLOPE算法

本文提出了一种基于随机顺序迭代和属性加权的新分类数据聚类方法RW-CLOPE。首先利用“洗牌”模型将数据集进行随机化打乱，然后对不同顺序的数据集进行聚类，选择收益值最大的聚类作为最优聚类，从而排除了输入数据顺序导致的聚类不稳定性问题；其次，根据每一维属性对聚类贡献度的不同，给每一维属性赋予不同的权值并提出一个新的全局评估函数，其定义如下：

定义2 令X={x1,x2,…,xn}表示待聚类的数据集，xi={i1,i2,…,im}表示第i个样本，聚类后的簇集为C={C1,C2,…,CL}。用occ(i,j,C)表示属性i在簇C中第j维出现的频率，Oj为在第j维上属性的集合，wj为簇中第j维属性对应的权值，用D(Ck)表示簇Ck中所有属性项取值的集合。定义直方图的面积S(Ck)及宽度W(Ck)如下：

(7)

(8)

此时，该算法的全局评估函数为：

(9)

其中r为簇内控制记录相似度的排斥因子，L为簇的个数。

RW-CLOPE算法通过比较前后两轮迭代的收益值来判断算法是否收敛，并将每一轮最优聚类对应的数据集作为下一轮迭代的输入数据集。随着迭代次数的增加，profit值也不断增加并最终趋于一个稳定值，当profit值不再变时，我们认为profit值取到全局最优，即聚类质量达到全局最优。其中RW-CLOPE算法的首轮迭代大致分为两个阶段：初始化及迭代阶段。在初始化阶段，利用“洗牌”模型生成预定义份数的数据，对每一份随机顺序根据profit最大化的原则得到初始聚类。在迭代阶段，根据profit最大化的原则对第一阶段得到的每份初始聚类进行调整，针对每一份随机顺序都得到一个最优聚类，然后选择profit值最大的聚类作为本轮的最优聚类。在后续的每轮迭代中，通过洗牌模型对数据进行打乱，然后根据打乱后的记录顺序，对前一轮的最优聚类划分进行调整，直至算法收敛。具体的算法如下：

算法2 RW-CLOPE算法

/* 第1阶段：初始化 */

(1)通过“洗牌”将原始数据顺序打乱，得到n份不同随机顺序的数据集D={D1,D2,…,Dn}，n为用户定义的数据份数

(2)forDk∈{D1,D2,…,Dn}

(3) whileDk中有未被读取的记录

(4) 读取一条记录

(5) 根据profit最大化原则，将记录t放入已有或新建的第i个簇中，更新簇对应的权值向量

(6) 将记录写回数据集Di

/*第2阶段：迭代 */

(7)while(not convergence)

(8) repeat

(9) forDk∈{D1,D2,…,Dn}

(10) whileDk中有未被读取的记录

(11) 从Di中读一条记录

(12) moved = false;

(13) 将记录移动到使profit最大的簇Cj中，同时更新簇对应的权值向量

(14) ifCi≠Cj

(15) 将记录写回数据集Dk

(16) moved = true;

(17) endif;

(18) 选择收益值最优的聚簇及对应的数据集Dm

(19)until moved=false

3.4 并行实现

从3.3节可知，RW-CLOPE算法的每一轮迭代都先将输入数据集随机打乱成d(预定义值)份数据集，然后分别对不同顺序的数据集进行聚类。再将该轮迭代的最优聚类划分作为下一轮迭代的输入，反复迭代，直至得到最优的聚类划分。在串行实现中，算法的每一轮迭代都需要重复的执行“洗牌”操作和加权CLOPE聚类，以得到d份顺序不同的数据集及d份数据集对应的最优聚类。为了提升算法的执行效率，本文将前后无关联的任务分布地运行在不同节点上。在数据变序阶段，通过广播将输入数据集的信息发送至每个节点，然后并行的在每个节点上执行“洗牌”操作，最后得到d份与输入数据集顺序不同的数据集。此后，将每一份数据的加权CLOPE操作放在不同计算单元上独立完成，而比较全局收益值的计算统一放在一个计算单元上处理。在这个过程中，先并行打乱数据顺序再并行计算最后全局比较收益值的大小，为并行聚类的实现提供了可能性。

我们在分布式基础架构Spark上实现了RW-CLOPE算法，使用HDFS存储数据，利用Spark中RDD的操作执行算法的并行化。具体来说，首先将待聚类的数据集D以指定的文本格式上传到HDFS，通过Spark的广播机制将数据集D信息分发到不同节点。然后在不同的节点上并行地执行“洗牌”操作，得到d份顺序不同的数据集。其中，每得到一份数据集便将其分发到一个Map任务进行一轮迭代的聚类。等所有Map任务结束后，通过一次Reduce过程，比较d份数据集的收益值，选取收益值最大的数据集作为下次迭代的输入数据。依次迭代，当最优聚类中的所有记录都没有移动时，聚类过程结束，即得到为全局最优聚类划分。执行流程如图2所示。

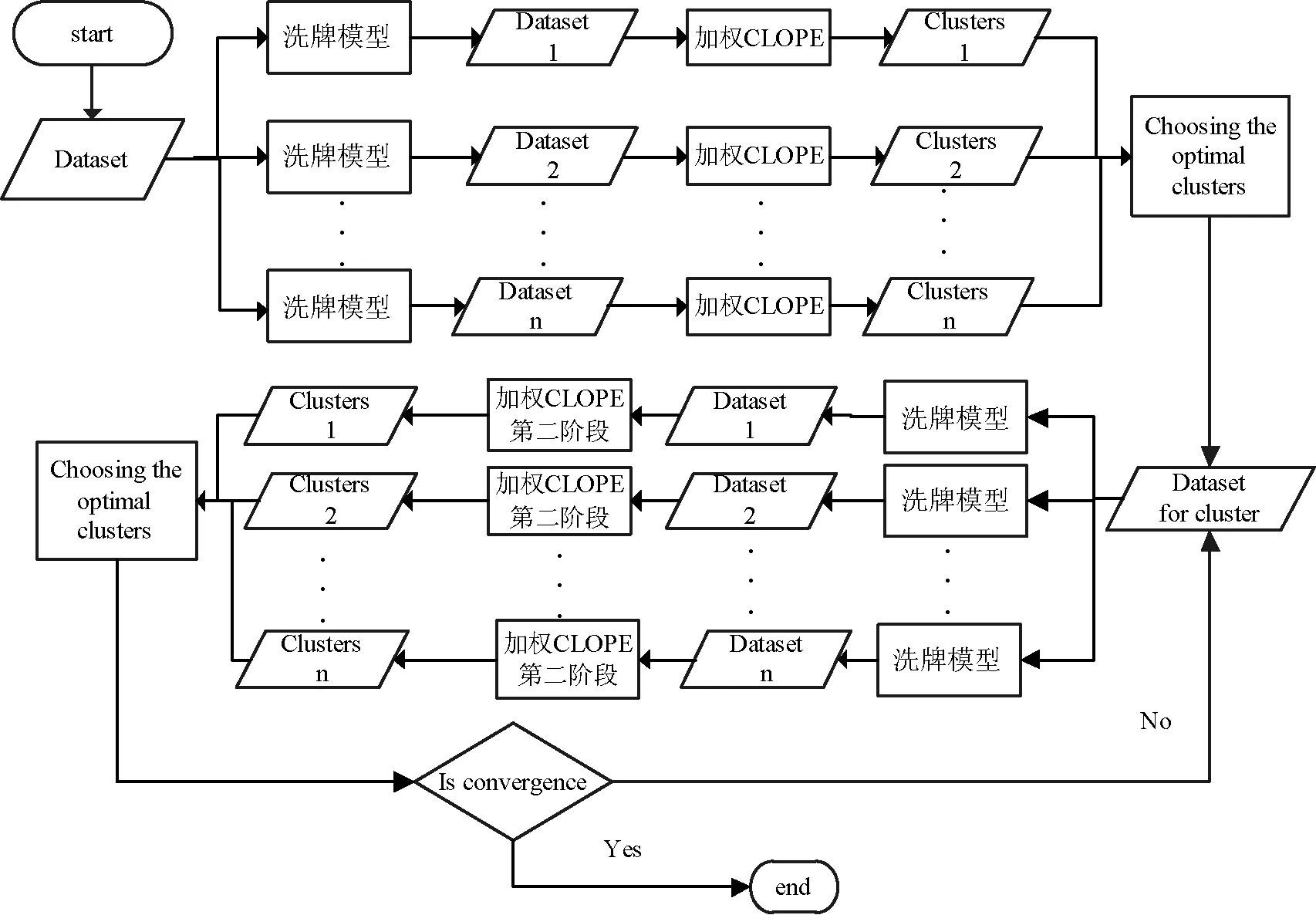
图2 RW-CLOPE执行流程图

在数据变序阶段，与p-CLOPE算法中在单节点上进行数据的所有打乱操作相比，RW-CLOPE利用Spark中RDD的并行化操作，并行的执行“洗牌”模型，使其以较小的时间代价得到离散程度更为彻底的随机数据。此外，RW-CLOPE算法是基于Spark平台实现的，相比较于Hadoop平台将中间结果存入硬盘的方法，Spark将中间结果或常用数据存入内存，很大程度上减小了算法在中间结果上的时间开销。

3.5 时间与空间复杂度

CLOPE算法一次迭代的时间复杂度是O(N×K×A)，空间复杂度为O(M×K)。其中A是每天记录的平均长度，N是总的记录数，K是簇的个数,M为维度。与CLOPE算法相比，在每一轮迭代中，RW-CLOPE需要通过“洗牌”操作得到d份顺序不同的数据集，然后对d份数据集分别进行聚类操作。其中“洗牌”操作每执行一次的时间复杂度为O(N)，所以RW-CLOPE算法每一轮迭代的时间复杂度为O(d×N2×K×A)，空间复杂度与CLOPE相当。RW-CLOPE算法在每轮迭代后都选出本轮的最优聚类作为下一轮迭代的输入，所以能以更少的迭代次数达到收敛。

4 实验与分析

本文主要的贡献有如下3个方面：首先利用“洗牌”模型随机地打乱数据集的排列顺序，再对不同顺序的数据集进行聚类，选择profit值最大的聚类作为最优聚类，克服了CLOPE算法受数据集顺序而导致的聚类质量不稳定问题。其次，根据每一维数据的信息熵，为每一维数据引入权值并将权值的更新自动化，极大程度上提升了聚类的质量。最后，在实现上，结合Spark平台的特性，使其能高效地处理海量数据。本文实验对比的对象为CLOPE算法及其同类算法p-CLOPE。实验采用的3组数据集分别是蘑菇数据集、大豆疾病数据集以及美国人口普查数据集。在前两个数据集中，主要比较了聚类质量。由于美国人口普查数据集规模较大，在该数据集中分别从聚类质量，时间性能两个方面进行比较。实验采用本文定义的全局收益值函数profit作为聚类质量评估指标，其数值越大，表明聚类质量越高。其中，CLOPE与p-CLOPE在计算profit时，默认每维属性的权重相等，权值为1/维度。

实验所使用的p-CLOPE实现代码来自文献[8]，CLOPE算法代码是严格地按照文献[1]的思想进行实现的。CLOPE运行在单机上，p-CLOPE算法与RW-CLOPE算法分别运行在由7台单机搭建的Hadoop及Spark集群上，每个节点的配置为8 GB的内存，i7处理器。

4.1 蘑菇数据集

蘑菇数据集(Mushroom)也是原CLOPE算法测试过的数据集，来自加州大学欧文分校机器学习库，包含记录数为8 124，其中每条交易由22个属性组成，根据是否可食用分为两个类别。所有的属性项共有116个不同的值，其中2 480个缺失属性值用问题号‘?’表示。

以下分别在数据集份数d取不同值的条件下用RW-CLOPE、CLOPE执行聚类，用本文提出的profit作为衡量聚类质量的指标进行测试，实验结果如图3所示。其中X轴为排斥因子，Y轴为RW-CLOPE、CLOPE对应的profit的比值。

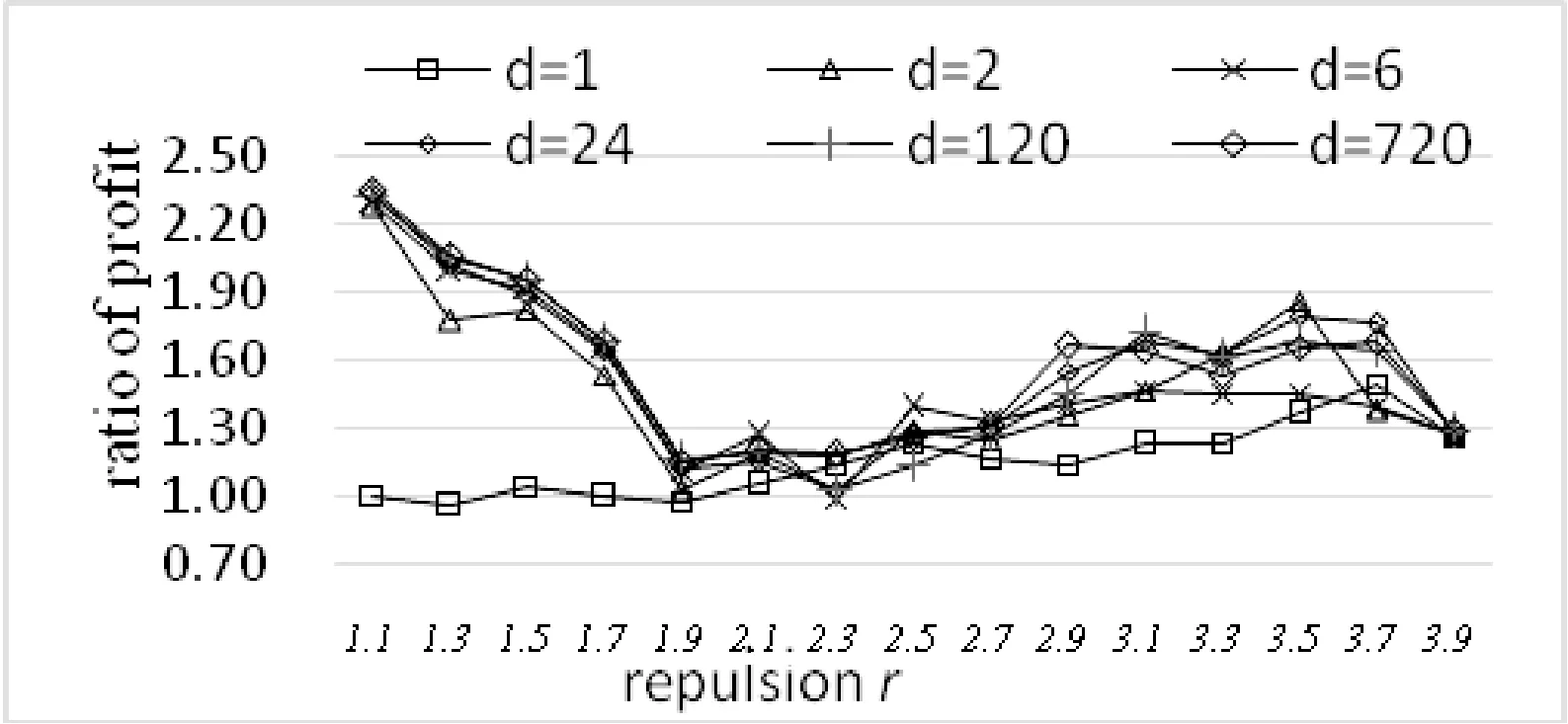
图3 蘑菇数据集RW-CLOPE与CLOPE对比图

从图3中可知，RW-CLOPE算法的聚类质量明显优于CLOPE，即经过“洗牌模型”及数据维加权这两个步骤后，算法的聚类质量得到了明显的提升。因此，下文中的实验，我们只将RW-CLOPE与CLOPE的同类改进算法p-CLOPE进行比较。实验中排斥因子r步长0.2，取值为1.1～3.9，d的取值为1、2、6、24、120、720对应于p-CLOPE算法中p取1～6时产生的数据份数，其实验结果如图4所示。

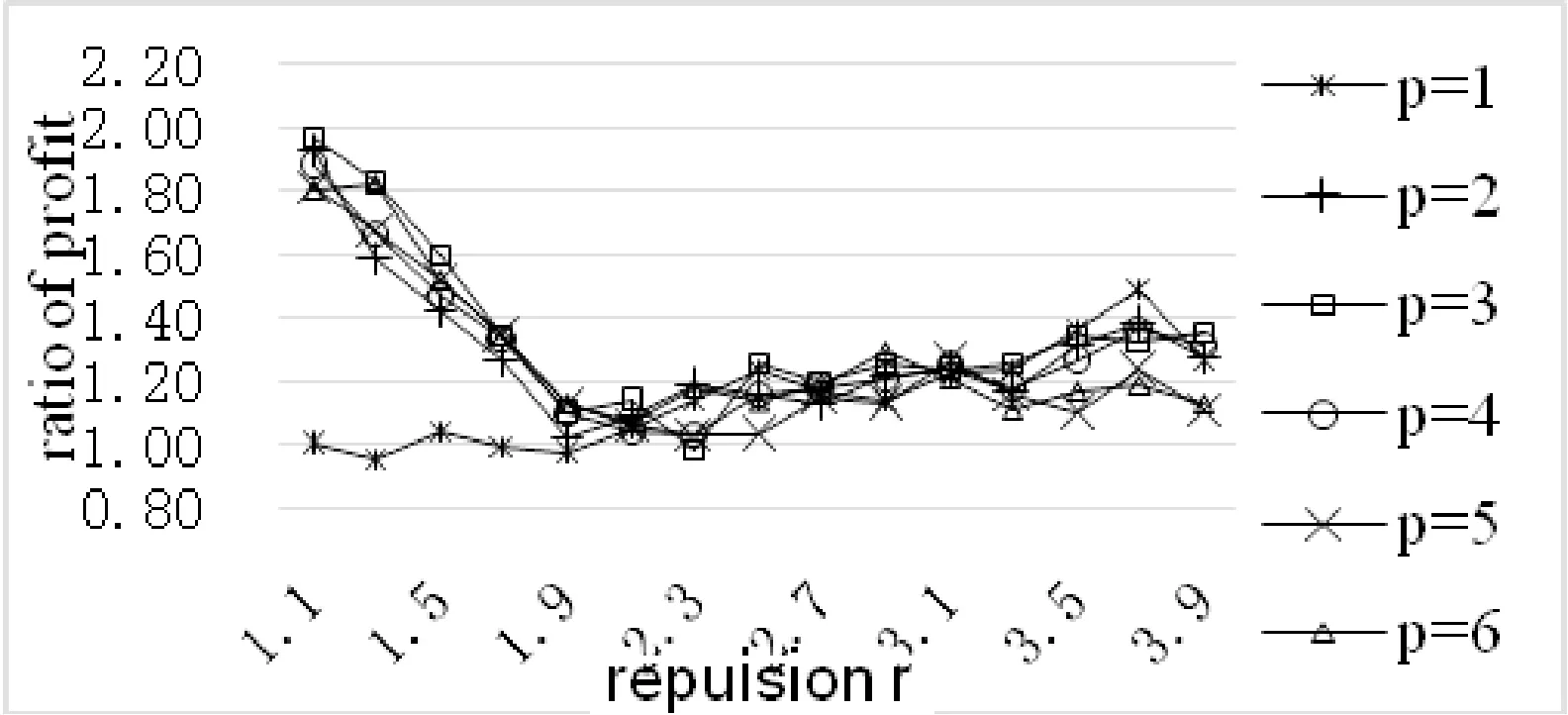
图4 蘑菇数据集p-CLOPE实验对比图

从图4中可以看出在d取不同值时，大多情况下RW-CLOPE与p-CLOPE profit的比值均大于1，即RW-CLOPE的聚类质量优于p-CLOPE。在文献[1]中，CLOPE算法的聚类质量在r=3.1时取得最佳值。在文献[8]中，当r=3.1时，p-CLOPE的收益值相对于CLOPE提升了35.1%。如图4所示，本文实验中RW-CLOPE在相同的条件下(r=3.1，p=4)，收益值比p-CLOPE大25%。

4.2 大豆疾病数据集

大豆疾病数据集(Soybean)共307条记录，每个记录由35个属性组成，根据疾病的种类，数据样本被分为19类。数据来自加州大学欧文分校机器学习库，分别用p-CLOPE与RW-CLOPE对其执行聚类，并比较d取不同值时的聚类收益值。实验结果如图5所示。

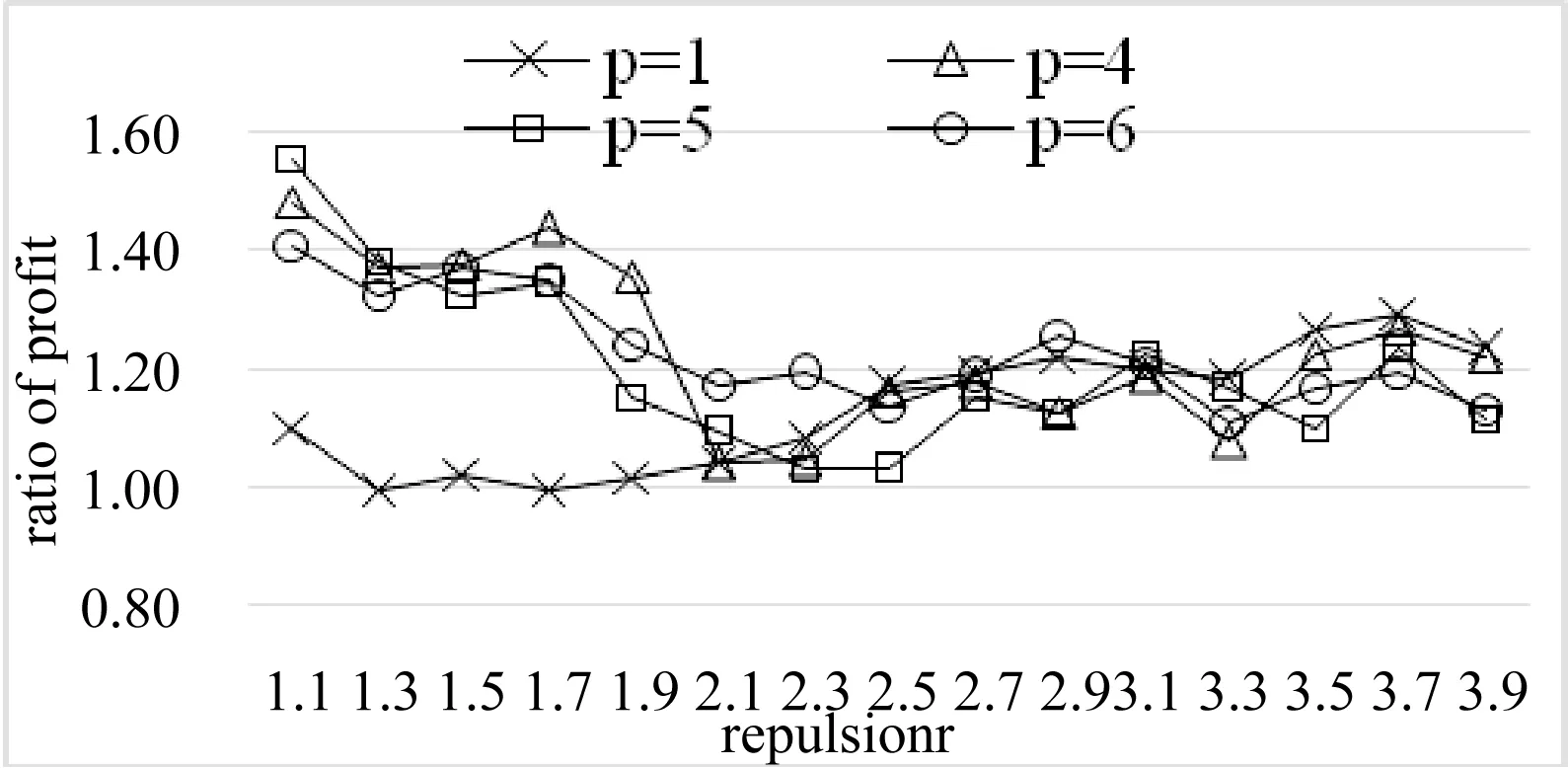
图5 大豆疾病数据集实验对比图

对比图4与图5，我们发现在d相同时，大豆数据集对应的收益比值总体上小于蘑菇数据集对应的比值。这是因为RW-CLOPE与p-CLOPE的profit比值和数据集中的记录数相关，当记录较少时，数据通过等分再划分得到的离散程度与通过“洗牌”模型得到的离散程度之间的区别小，因此这两种打乱数据排序的方法对聚类的质量区别相差不大。此外，如图5所示，在d取不同值时，RW-CLOPE与p-CLOPE的收益比值总体上大于1。这是因为RW-CLOPE算法考虑到属性维对聚类结果存在贡献度的区别性，因此根据属性维的信息熵给赋予不同的权值，从而极大程度上提升了聚类的质量。

4.3 美国人口普查数据集

美国人口普查数据集是从1990年美国人口普查全样本数据中按1%的比例抽取的公共使用微数据样本。包含的记录条数2 458 285，数据由祖先、族群、拉美族裔来源、行业职业、语言、出生地等领域的68个属性组成。与前2个数据集相比，这个数据集的交易条数达到百万级别。当数据打乱份数d取不同值时，分别用RW-CLOPE与p-CLOPE执行聚类，实验结果如图6所示。

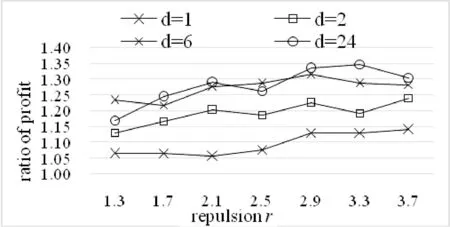
图6 美国人口普查数据集

在图6中，d取值为6、24(即p-CLOPE中p的取值为3、4)时，对应的RW-CLOPE与p-CLOPE的收益比值大于d取值为1、2时的收益比值，这是因为d值越大对应的数据份数越多。论证了CLOPE算法的聚类质量受数据的输入顺序的影响。相比于蘑菇数据集的实验结果，我们发现在d=24，排斥因子取较大值时(也是实际有意义的情况)。在数据份数相同时，美国人口普查数据集对应的RW-CLOPE与p-CLOPE的收益比值大于蘑菇数据集对应的收益比值，这是因为数据量越大，“洗牌”模型相对于原始的等分划分再排列的方式对数据的打乱就越彻底，因此RW-CLOPE算法越趋近于全局最优聚类。在图6中，当d=1时，收益比值总体上大于1，这说明在输入顺序一致的情况下，加权CLOPE算法的聚类质量高于没加权CLOPE。

在这组百万数据集下，我们还比较了p-CLOPE算法与RW-CLOPE算法在d取不同值时的执行时间。其中X轴坐标为排斥因子r，r的取值2.9、3.1、3.3、3.5，因为在p-CLOPE算法的实验结果中，r取这四个取值时对应的聚类结果最优。Y轴为RW-CLOPE与p-CLOPE的执行时间比，实验结果如图7所示。

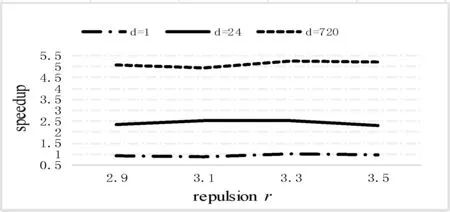
图7 执行时间对比图

从图7中我们可以看到，d数值越大，RW-CLOPE与p-CLOPE的执行时间的比值也越大。这主要的原因是，p-CLOPE在中间结果上的时间开销随着d的增大而增大，由于受到实验环境的限制，这个实验中d的最大取值为720。

5 结 语

本文提出了一种基于随机顺序迭代和属性加权的新分类数据聚类方法——RW-CLOPE。在聚类质量方面，首先利用“洗牌”模型对数据集的顺序进行随机化打乱，提高聚类质量的稳定性。其次，根据分类数据的信息熵给不同的属性维赋予不同的权值来区分其对聚类质量的贡献度，极大程度上提高了聚类的质量。在实现上，RW-CLOPE算法在Spark平台上进行了实现，使其能快速的处理海量数据。在3个真实数据集上的实验表明，RW-CLOPE算法比p-CLOPE算法取得更优的聚类结果，处理海量数据时有更好的扩展性。

[1] Yang Y,Guan X,You J.CLOPE:A fast and effective clustering algorithm for transactional data[C]//Proc of the 8th ACM SIGKDD Int Conference on Knowledge Discovery and Data Mining.New York:ACM,2002:682-687.

[2] Kok-Leong Ong,Wenyuan Li,Wee-Keong Ng.SCLOPE:An algorithm for clustering data streams of categorical attributes[C]//Knowledge-Based Intelligent Information and Engineering Systems,2004,3181:209-218.

[3] Li Y F,Le J J,Wang M,et al.MR-CLOPE:A Map Reduce based transactional clustering algorithm for DNS query log analysis[J].Journal of Central South University,2015,22(9):3485-3494.

[4] 彭雅丽,章志明,余敏.一种改进的CLOPE算法在入侵检测中的应用[J].微计算机信息,2006,8(24):58-60.

[5] Guha S,Rastogi R,Shim K.ROCK:A robust clustering algorithm for categorical attributes[C]//Proc of the 15th Int Conference on Data Engineering(ICDE 1999).Los Alamitos,CA.IEEE Comuter Society,1999:23.

[6] Wang K,Xu C,Liu B.Clustering transactions using large items[C]//Proc of the 8th Int Conference on Information and Knowledge Management.New York:ACM,1999:10.

[7] Li Jie,Gao Xinbo,Jiao Licheng.Fuzzy CLOPE algorithm and its parameter optimalchoice[J].Control and Decision,2004,19(11):1250-1254.

[8] 丁祥武,郭涛,王梅.一种大规模分类数据聚类算法及其并行实现[J].计算机研究与发展,2016,53(5):1063-1071.

[9] Xiong T,Wang S,Mayers A,et al.DHCC:Divisive hierarchical clustering of categorical data[J].Data Mining and Knowledge Discovery,2012,24(1):103-135.

[10] Li T,Ma S,Ogihara M.Entropy-Based criterion in categorical clustering[C]//Brodley CE. Proc.of the 21st Int’1 Conference on Machine Learning.Banff:ACM Press,2004:68.

[11] Christian P,Dickman B H,Gilman M J.Monto Carlo optimization[J].Journal of Optimization Theory and Applications,1989,60(1):149-157.

[12] Huang Zhexue.Extensions to the k-means algorithms for clustering large data sets with categorical values[J].Data Mining and Knowledge Discovery,1998,2(3):283-304.

[13] Huang Zhexue,Ng M K.A fuzzy k-modes algorithm for clustering categorical data[J].IEEE Transactions on Fuzzy Systems,1999,7(4):446-452.

[14] Gan G,Wu J,Yang Z.A genetic fuzzy k-modes algorithm for clustering categorical data[J].Expert System with Application,2008,36(2):1615-1620.

[15] Chan E Y,Ching W K,Ng M K,et al.An optimization algorithm for clustering using weighted dissimilarity measures[J].Pattern Recognition,2003,37(5):943-952.

[16] Andritsos P,Tzerpos V.Evaluating value weight schemas in the clustering of categorical data[C]//1stWorkshop on Machine Learning and Intelligent Optimization(LION),2007.

A CLUSTERING ALGORITHM OF CATEGORICAL DATA AND ITS EFFICIENT PARALLEL IMPLEMENTATION

Ding Xiangwu Tan Jia Wang Mei

(CollegeofComputerScienceandTechnology,DonghuaUniversity,Shanghai201620,China)

For large-scale, high-dimensional, sparse categorical data clustering, compared with the traditional clustering algorithm, CLOPE has a great improvement in the quality of clustering and running speed. However, CLOPE has some defects such as clustering quality instability, not to distinguish the attribute clustering contribution between each dimension, need to specify rejection factor r in advance. Therefore, this paper proposes a clustering algorithm for categorical data based on random sequence iteration and attribute weight (RW-CLOPE). RW-CLOPE use the “shuffle” model to sort the raw data randomly to eliminate the effect of data input sequence on clustering quality. At the same time, based on the information entropy, the calculation method of attribute weights is proposed to distinguish the attribute clustering contribution between each dimension which greatly improve the quality of data clustering．Finally, the RW-CLOPE algorithm has been implemented on the efficient cluster platform—Spark. Experiments on three different and real data show that RW-CLOPE algorithm achieves better clustering quality than p-CLOPE algorithm when the number of disordered dataset is the same．For the mushrooms dataset, when CLOPE achieve optimal results, RW-CLOPE can achieve 68% higher profit value than CLOPE and 25% higher profit value than p-CLOPE．The execution time of RW-CLOPE algorithm is much shorter than p-CLOPE algorithm when dealing massive data．When the computational resources are sufficient, the more the number of data sets in, the more obvious the improvement of the execution time is.

Categorical data CLOPE p-CLOPE RW-CLOPE Spark

2016-08-18。上海市信息化发展资金项目(XX-XXFZ-05-16-0139)。丁祥武，副教授，主研领域：大数据和列存储技术，分布式处理，多核及众核并行技术。谭佳，硕士。王梅，教授。

TP312

A

10.3969/j.issn.1000-386x.2017.07.046