基于压缩感知的GPS信号压缩与捕获研究
何国栋 ,汪佳瑞 ,靳蓓蓓 ,王涛春
(1. 安徽师范大学 物理与电子信息学院,安徽 芜湖241003;2. 安徽师范大学 数学计算机科学学院,安徽 芜湖 241003)
基于压缩感知的GPS信号压缩与捕获研究
何国栋1,汪佳瑞1,靳蓓蓓1,王涛春2
(1. 安徽师范大学 物理与电子信息学院,安徽 芜湖241003;2. 安徽师范大学 数学计算机科学学院,安徽 芜湖 241003)
全球定位系统(Global Position System,GPS)信号的捕获是其应用的关键步骤,直接影响系统的正常运行。针对卫星导航信号所具有的稀疏特性,结合压缩感知理论稀疏性的要求,设计了基于卫星特性的稀疏字典,应用随机矩阵对信号进行压缩,获得GPS压缩信号,通过正交匹配追踪算法对压缩后的GPS信号进行捕获。最后通过大量的仿真实验验证了该方法的可行性,可以将其应用于 GPS数据压缩、高信噪比快速捕获及GPS信号源中。
压缩感知;全球定位系统;捕获;正交匹配跟踪
0 引言
GPS采用码分多址扩频调制信号,GPS 信号高效准确的捕获,是影响导航接收机正常工作的关键因素[1-2]。目前已有大量的文献对GPS信号的捕获进行了研究,常用的捕获方法有串行捕获、基于FFT的并行快速捕获和微弱信号的长时累积捕获[3-4]等。
Nyquist采样定理指出采样频率必须高于信号最高频率的2倍,这对高频通信系统的采样无疑是一个重要的制约因素,因此需要寻找新的理论突破。为解决这一技术发展的瓶颈,2006年Candès、Tao和Donoho等[5-6]人提出了压缩感知的理论:对于稀疏或在某个字典下稀疏的信号,可以以远低于Nyquist采样速率对信号进行采样,并可以通过重构算法实现信号的完美重构。压缩感知充分利用了信号的稀疏特性,可大大降低信号的采样速率,减少采样数据,给信号的后期存储、传输和处理带来很大的便利。目前,压缩感知得到了全球研究人员的广泛关注,其应用的领域涉及模拟到信息转换[7-8]、图像处理[9]、无线通信[10]及医学等[11]。
由于卫星PRN码互相关具有稀疏特性,符合压缩感知理论的稀疏性要求,并根据不同的卫星信号设计稀疏字典,应用随机矩阵对接收的下变频信号进行压缩,获得GPS压缩信号。通过改进的匹配追踪算法对压缩后的GPS信号进行捕获。仿真实验验证了该方法的可行性,可以在高压缩率下对高信噪比信号准备捕获,可以对实际GPS信号进行压缩、捕获,或应用于GPS信号源中。
1 传统的GPS信号并行捕获算法
射频前端接收的GPS信号通过下变频后变为中频信号,第k个卫星信号的数学表达式为:

(1)
式中,Ck(t)为第k个卫星的PRN码,Dk(t)为导航电文,ωI为中频频率,ωd为卫星和接收相对运动产生的多普勒频移,θk为载波相位,n(t)为噪声干扰。
捕获的目的是为了粗略决定可见卫星的载波频率和码相位,传统的码分多址系统经常采用串行搜索捕获方法,对所有卫星可能的码相位和频率进行二维搜索,计算量大,非常耗时。为了提高捕获的效率,Frai D M、Reichman A等人[12-13]提出了并行捕获算法,将二维搜索的一个域进行并行搜索,大大提高了捕获的速度。
令2个长度为N的序列循环互相关序列为:

(2)
对式(2)进行N点离散傅里叶变换,得到:

(3)
式中,X*(k)为x(n)的傅里叶变换的共轭,Y(k)为y(n)的傅里叶变换的共轭。通过一次傅里叶逆变换,即可找到初始码相位。根据上面的公式,并行码相位捕获原理如图1所示。
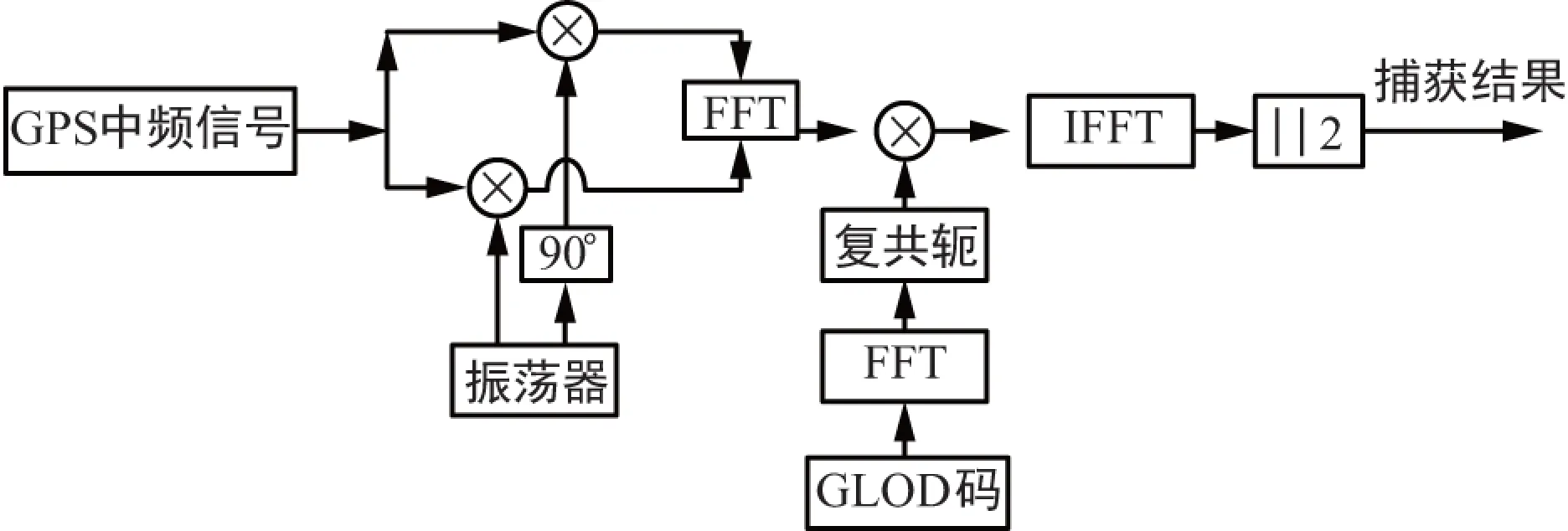
图1 GPS并行码捕获算法原理图
2 压缩感知
基于Nyquist采样频率的数据采集,没有考虑信号内部的相关性,得到大量的冗余数据,然后对其进行压缩,降低数据量。压缩感知充分利用了数据的稀疏性,将数据的冗余采样和压缩合二为一,直接得到较少的采样数据,给信号处理带来便利。压缩感知主要包含3个部分:信号的稀疏表示、测量矩阵和重构算法,下面简单介绍这个3个部分的组成原理[14]。
2.1 信号的系数表示
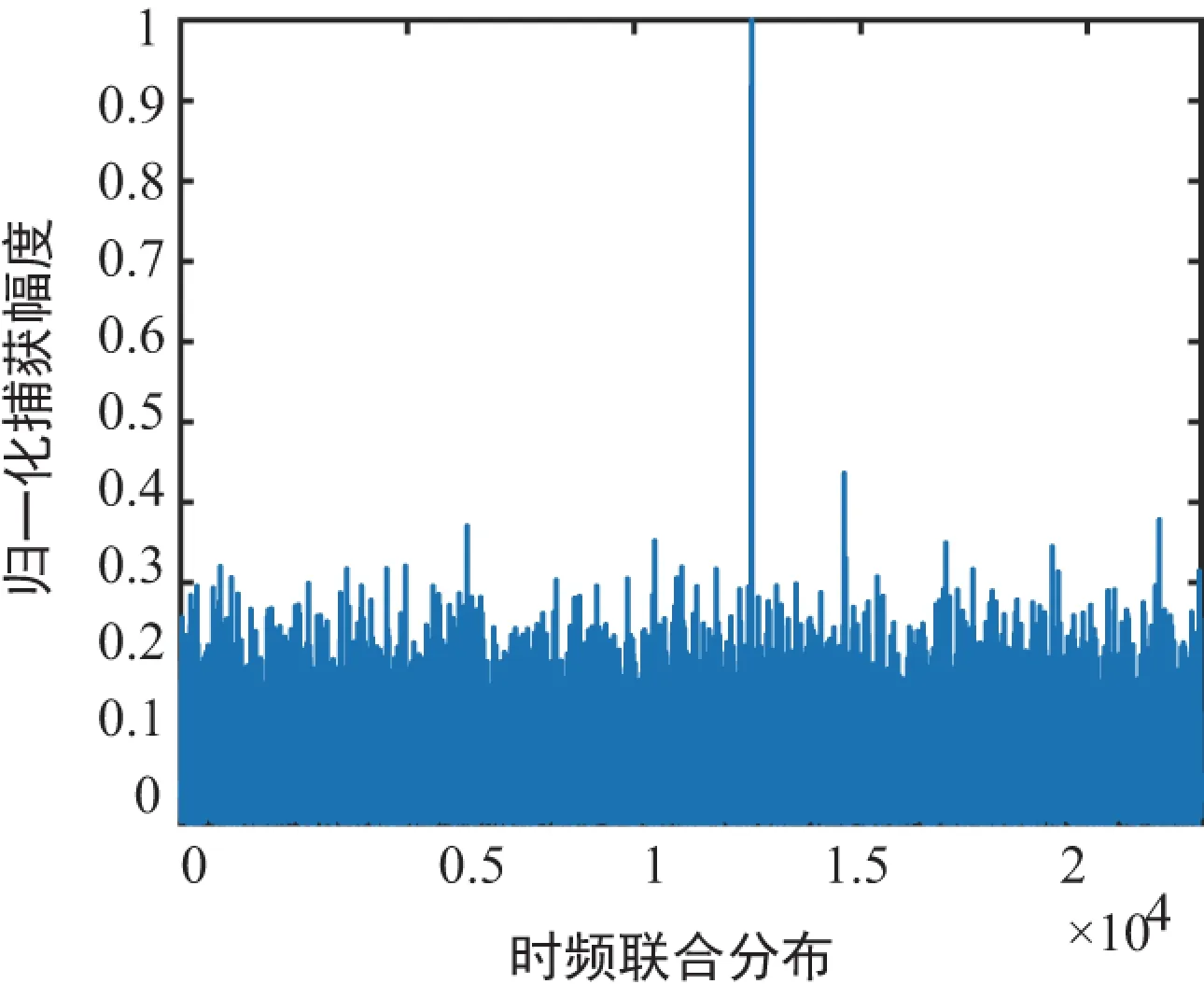
给定信号x的长度为N,如果这个信号中大部分元素为零,只有k(k< x=Ψ·s, (4) 式中,s只有较少的非零元素,常用的基有离散余弦变换、离散傅里叶变换、小波变换和非正交冗余字典等。压缩感知应用的前提是信号必须是稀疏的,所以信号的稀疏表示至关重要。 2.2 测量矩阵 测量矩阵Φ是一个M×N(M< Y=Φ·x=Φ·Ψ·s=Θ·s。 (5) 通过测量获得了长度为M测量信号Y,实现了对信号的压缩。将式(5)中Φ*Ψ=Θ测量矩阵和字典合在一起称为感知矩阵。 测量矩阵与基或字典必须满足不相关性,其不相关公式定义为: (6) M≥c·u2(Φ,Ψ) ·k·ln(N)。 (7) 可以看出,M与相关值成正比,所以一般选用相关值较低的矩阵作为测量矩阵。常用的测量矩阵有Toeplitz矩阵、高斯分布的随机矩阵和哈达码矩阵等。 2.3 重构算法 从式(5)的测量过程可以看出,这是一个未知数比方程数多的欠定方程,该方程有无穷多组解,理论分析已经证明,在满足不相关性和稀疏性的条件下,可以通过重构算法重构出原稀疏信号。基于优化的求解可以表示为: (8) 式中,‖‖0为求信号中的非零元素的个数,但是上式的求解是一个NP-hard问题,可以通过其他算法进行求解,常用的求解方法有基追踪算法、迭代法贪婪算法等。 根据压缩感知的理论和GPS信号的特点,提出了一种基于压缩感知的GPS信号压缩与捕获方法。应用随机矩阵对GPS信号进行压缩,根据卫星特性构造字典,并通过改进的匹配追踪算法对卫星进行捕获,其构成分为以下两个部分。 3.1 稀疏字典的构造 在GPS串行捕获方法中,通过码片移位和多普勒频移二维搜索寻找卫星,其公式表示为: (9) (10) 当本地产生的信号与接收信号的GOLD码时间移位C(n-τ)和多普勒频率e-jwdn都对齐时,会得到较强的相关峰,而在其余情况下该值都相对较小,也即捕获结果是稀疏的,这与压缩感知所描述的稀疏信号相符合,基于此捕获原理设计稀疏字典。 字典包含1 023个GOLD码片的循环移位和多普勒频率的搜索范围,一般多普勒频率搜索范围为±10 kHz,搜索步进为500 Hz,有41个频率点,所以字典ψ=[Cn-τ·e-jωdn]∈Rn×(λ×41×1023),其中λ为每个码片的采样点数,n为压缩前数据的总长度。对于一颗卫星,如果接收的信号中含有该卫星发射的信号,则会有一个很强的相关峰值,而其余值都相对较小,即信号在该字典中可稀疏表示。 3.2 重构算法 压缩感知重构算法很多,贪婪类算法中的匹配跟踪算法重构速度较快,适合工程应用。考虑卫星系统的特殊性,即如果含有该卫星信号,则相关峰很强,而其余值都很弱。正交匹配追踪算法可以重构出原稀疏信号[15-16],但是考虑GPS信号捕获只需找到其对应卫星的码相移和多普勒频率,设计了一种基于以上构造的稀疏字典正交匹配追踪算法来捕获卫星信号[17],算法具体步骤如下: 初始化:输入基于GPS伪码和多普勒的稀疏字典,压缩观测信号,残差r0=y; Step1:找出残差和感知矩阵相关积最大值对应的下标λ,即[Rk-1,λ]=argmaxj=1...N‖rk-1,Θj‖2; Step3:计算最小二乘得到 Step5:判断是否满足迭代条件,设定捕获阈值Thresh,不满足则继续执行Step1,如果R2/R1≥Thresh,则认为捕获到一颗卫星,反之认为没有该颗卫星信号,捕获结束。 为了验证本文提出的基于压缩感知的GPS信号压缩和捕获方法,应用Matlab对其进行仿真,其中测量矩阵使用的是归一化的零均值高斯分布随机矩阵,码相位搜索步长为半个码片,多普勒频率步长搜索为500 Hz,为简化仿真,多普勒频率搜索范围为-2.5 ~2.5 kHz。人为构建一颗卫星信号,随机产生码移位和多普勒频移,构造模拟的GPS信号,应用随机观测矩阵对信号进行压缩,并应用本文方法对其进行压缩捕获。 仿真以1号卫星为例,产生其对应的GOLD码,采样频率Fs=38.192 MHz,中频频率Fc=9.548 MHz,多普勒频偏和伪码相移使用随机产生的一个值,例如下面捕获仿真中随机产生的多普勒频移Fd=0.657 7 kHz,伪码相移Td=5 890,生成1 ms卫星信号。实验分为无噪声、高信噪比(10 dB)和低信噪比(-10 dB)3组,噪声类型为零均值加性高斯白噪声,分析其抗噪声性能;每组又分别包含压缩率α为70%、80%和90%三种情况,压缩率定义由式(11)给出,从压缩率和噪声强度两方面分析GPS信号压缩与捕获的关系。 (11) 对产生的1 ms信号分别进行100次蒙特卡洛实验,给出了9组实验中低信噪最低的捕获结果图,如图2所示,因为这是最差捕获环境,其余结果都比这种情况好。正确的多普勒频率值为:5+ceil(0.655 7×103/500)=6,码相位为ceil(38 192/5 890)=6.5,实验捕获的峰值位置为12 592,按照上面给出的字典构成原理反求对应的频率点和相位点,也即捕获的频率点为12 592/2 046=6.15,相位:2 046/(12 592-2 046*6)=6.47。 通过仿真发现,在无噪声、高信噪比和高压缩率情况下均可以实现卫星的正常捕获,但是在低信噪比情况下,当压缩率为90%(即只保留了10%的采样数据)时,很难对卫星正确捕获。 (a)压缩率为70% (b)压缩率为80% (c)压缩率为90% 提出了一种基于压缩感知的GPS信号压缩与捕获方法,分析了GPS信号的稀疏特性,并根据卫星特性和压缩感知理论构造了稀疏字典,应用随机矩阵对信号进行了压缩,并应用稀疏重构算法对卫星进行捕获。通过大量仿真实验验证了该方法的可行性,可以将其思想应用到GPS数据的压缩或模拟信号源中。本文提出方法在高压缩率和低信噪比下捕获效果较差,如何提高其性能将是进行后续研究的重要方向。 [1] Braasch M S,Van A J. GPS Receiver Architectures and Measurements[J]. Proceedings of the IEEE,1999,87(1):48-64. [2] Kai B,Akos D M,Bertelsen N,et al. A Software-Defined GPS and Galileo Receiver[M]. Boston:Birkhäuser Boston,2007. [3] 陈希,张锐,帅涛. 基于FFT的GPS快速并行捕获算法[J]. 宇航学报,2011,32(1):162-166. [4] 唐琳琳. L1/L2C双频车载GPS软件接收机快速捕获算法研究[D]. 南京:南京航空航天大学,2015. [5] Candès E J,Romberg J,Tao T. Robust Uncertainty Principles: Exact Signal Reconstruction from highly Incomplete Frequency Information[J]. Information Theory,IEEE Transactions on,2006,52(2): 489-509. [6] Donoho D L. Compressed Sensing[J]. Information Theory,IEEE Transactions on,2006,52(4): 1289-1306. [7] 何国栋,杨凌云,谢小娟,等. 基于压缩感知的模拟到信息转换研究[J]. 无线电通信技术,2015,41(1):21-23. [8] Kirolos S,Laska J,Wakin M,et al. Analog-to-Information Conversion via Random Demodulation[C]∥Design,Applications,Integration and Software,2006 IEEE Dallas/CAS Workshop on. IEEE,2006: 71-74. [9] Romberg J. Imaging via Compressive Sampling[J]. Signal Processing Magazine IEEE,2008,25(2):14-20. [10]杨剑,蒋挺,赵成林,等. 基于CS-ROMP算法的超宽带信道估计[J]. 无线电工程,2011,41(5): 14-17. [11]Richy J,Friboulet D,Bernard A,et al. Blood Velocity Estimation Using Compressive Sensing[J]. IEEE Transactions on Medical Imaging,2013,32(11):1979-1988. [12]Frai D M,Reichman A. Fast Acquisition CDMA Receiver for Burst Transmission System[C]∥ IEEE International Conference on Electronics,Circuits and Systems. IEEE,2004:342-345. [13]Tang B,Liu S,Tang W,et al. Design a L1 Software GPS Receiver Based on IF GPS Signal Simulator[C]∥ International Conference on Signal Processing. IEEE Xplore,2006,3:109-115. [14]何国栋,谢小娟,杨凌云,等. 基于压缩感知的信号重构研究[J].无线电通信技术,2014,40(3):26-28. [15]Tropp J A,Gilbert A C. Signal Recovery from Random Measurements via Orthogonal Matching Pursuit[J]. Information Theory,IEEE Transactions on,2007,53(12): 4655-4666. [16]Tropp J A,Laska J N,Duarte M F,et al. Beyond Nyquist: Efficient Sampling of Sparse Bandlimited Signals[J]. IEEE Transactions on Information Theory,2010,56(1):520-544. [17]马庆涛. 压缩感知中的信号重构算法研究[D]. 南京:南京邮电大学,2013. Research on GPS Signal Compressing and Acquisition Based on Compressive Sensing HE Guo-dong1,WANG Jia-rui1,Jin Bei-bei1,WANG Tao-chun2 (1. College of Physics and Electronic Information,Anhui Normal University,Wuhu Anhui 241003,China; 2. School of Mathematics & Computer Science,Anhui Normal University,Wuhu Anhui 241003,China) The acquisition of GPS signal is a key step in its application,directly affecting the normal operation of system. In view of the sparsity of satellite navigation signals and the requirement of sparsity of compressive sensing theory,this paper designs a satellite-based features sparse dictionary. The GPS signal is compressed by random matrix to obtain the GPS compressed signal. The satellite can be acquired from compressed GPS signal by orthogonal matching pursuit. The results of multiple simulation experiments show that this method is feasible,and it can be applied to the GPS data compression,high SNR fast acquisition and GPS signal source. compressive sensing; GPS; acquisition; orthogonal matching pursuit 2017-03-30 国家自然科学基金项目(61402014);安徽省高校自然科学重点项目(KJ2016A266);安徽师范大学项目培育基金(2015xmpy16) 何国栋(1980—),男,副教授,硕士生导师,主要研究方向:压缩感知理论及其在信号处理中的应用等。王涛春(1979—),男,副教授,硕士生导师,主要研究方向:压缩感知理论与应用及无线传感器网络等。 10. 3969/j.issn. 1003-3114. 2017.05.09 何国栋,汪佳瑞,靳蓓蓓,等.基于压缩感知的GPS信号压缩与捕获研究[J].无线电通信技术,2017,43(5):38-41. [HE Guodong,WANG Jiarui,Jin Beibei,et al. Research on GPS Signal Compressing and Acquisition Based on Compressive Sensing [J]. Radio Communications Technology,2017,43(5): 38-41.] TP391.4 A 1003-3114(2017)05-38-4
3 基于压缩感知的GPS信号压缩与捕获
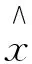
4 仿真与分析



5 结束语

