基于Jiles-Atherton理论的铁磁材料塑性变形磁化模型修正∗
刘清友 罗旭 朱海燕 韩一维 刘建勋
1)(西南石油大学机电工程学院,成都 610500)
2)(西华大学流体及动力机械教育部重点实验室,成都 610039)
3)(西南石油大学石油与天然气工程学院,成都 610500)
基于Jiles-Atherton理论的铁磁材料塑性变形磁化模型修正∗
刘清友1)2)罗旭1)†朱海燕3)韩一维1)刘建勋1)
1)(西南石油大学机电工程学院,成都 610500)
2)(西华大学流体及动力机械教育部重点实验室,成都 610039)
3)(西南石油大学石油与天然气工程学院,成都 610500)
(2016年10月10日收到;2017年3月10日收到修改稿)
Jiles-Atherton(J-A)模型在磁化建模领域应用广泛,但不同文献给出的J-A模型并不一致,致使采用不同表达式建立的塑性变形磁化模型存在多种版本,其正确性难以甄别.通过对无磁滞磁化方程、能量守恒方程和等效磁场强度方程的梳理与比较,发现原有模型中存在将磁化强度和无磁滞磁化强度混用、将不可逆磁化能量等效于全部的磁化能量、等效磁场强度中应力磁化项界定不清等问题.在此基础上,对上述方程进行了修正,推导了基于J-A模型的塑性变形磁化修正模型.将修正模型计算结果与原模型计算结果、相关文献中的试验结果进行对比,结果表明∶与原有计算模型相比,修正模型计算结果的饱和磁化强度和剩余磁化强度随塑性变形增加而减小,矫顽力随塑性变形增大而增大,达到饱和磁化强度时的外磁场强度随塑性变形增大而增大的趋势有所减弱,更符合试验结果,可更准确地反映塑性变形对材料磁化的影响.
∶Jiles-Atherton理论,磁滞回线,塑性变形磁化模型,力磁耦合
PACS∶75.80.+q,62.20.f—,75.30.Cr,75.60.EjDOI∶10.7498/aps.66.107501
1 引 言
塑性变形是改变铁磁材料磁化特性的重要因素之一.随着塑性变形增大,铁磁材料内部的位错密度增大,钉扎点增多,对磁畴运动的阻碍作用增强,从而使材料塑性变形区域磁特性发生显著改变.基于该效应,现已发展出多种电磁无损检测技术,如∶金属磁记忆检测技术、巴克豪森磁噪声技术、磁声发射技术.通过理论分析,确定塑性变形对材料磁特性的影响规律,建立准确、有效的塑性变形磁化模型,是实现塑性变形、应力集中等缺陷检测与反演的基础.
与Stoner-Wolhfarth(S-W)模型、Globus模型相比,J-A模型认为由于非磁性掺杂、位错、内应力等钉扎点的存在,使磁化过程受阻碍而导致磁滞,符合磁滞现象的物理本质,且模型参数较少、方便实现,在磁滞建模与仿真领域获得了广泛应用[1].J-A模型自身经历了一个发展过程∶研究早期,Jiles和Atherton采用改进的Langvein方程来拟合各向同性材料的无磁滞磁化曲线,再利用能量守恒原理,推导了磁滞回线的表达式[2];后来,又将实际磁化强度分为可逆磁化和不可逆磁化两部分,简化了J-A模型的计算过程[3−5].但是,在不同时期、不同文章中,Jiles等给出的模型表达式并不完全一致.例如文献[3—7]给出的无磁滞磁化强度曲线方程就不同于文献[8],基于可逆和不可逆磁化分量的J-A模型在文献[2—6,9]中也有三种不同表达.Stablik等[10−13],Suliga等[14],Wang等[15],Li等[16],Leng等[17]在利用J-A理论进行塑性磁化分析的过程中,根据不同文献中的J-A模型推导的塑性磁化模型也不一样,导致计算结果差异较大,不能准确反映塑性变形对材料磁化过程的影响.
本文在对J-A模型及塑性变形磁化模型进行系统归纳和分析的基础上,通过分析无磁滞磁化方程、能量守恒方程及磁场等效强度方程,指出了其中的不合理之处,并给出了上述方程的修正形式;在此基础上,重新推导了基于J-A理论的塑性变形磁化模型,并通过与原有模型计算结果、相关文献中的试验结果对比,验证了修正模型的有效性和准确性.
2 塑性变形对材料磁特性参数的影响
由图1所示[18],当施加的应力小于材料的屈服极限时,应变为弹性应变,且随着应力的增加呈线性增大;当施加的应力超过材料的屈服强度后,材料开始产生塑性应变,且随着应力的增大呈非线性增大,此阶段塑性变形εp=εf−εy,超过屈服极限的那部分应力通常被定义为应变硬化应力σF,根据Ludwik定理的定义[10]∶

式中,C和n为常数,与材料性质和形状有关.塑性变形使材料内部位错、晶格滑移密度增大,导致材料钉扎点增多.X射线检测结果表明,位错密度ζd与塑性变形εp呈比例关系[10]∶
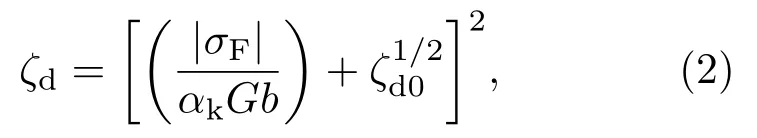
式中,αk为常数,取0.76;G为材料的剪切模量,G=Y/2(1+v);Y为杨氏模量;v为泊松比;b为柏氏矢量,是描述位错实质的重要物理量;ζd0为材料初始位错密度.
当材料存在塑性变形时,受位错密度ζd变化的影响,材料的钉扎系数k、无磁滞磁化曲线形状系数a均会发生改变,其与位错密度ζd的关系为[10]

式中,G1,G2,G3,G4为常数,且一般取G1=G3,G2=G4,可拟合得到;k0为初始钉扎系数;a0为初始无磁滞磁化曲线形状系数,可拟合得到;d为材料的晶粒尺寸,可实验测得.
此外,由于塑性变形改变了磁畴的形状和尺寸大小,因此,磁畴内部耦合的平均系数α也会随塑性变形的增加而发生变化,其与塑性变形的关系为[16]

式中,q1,q2,q3均为常数,可拟合得到.

图1 材料应力-应变曲线示意图 σf为加载应力,σy为材料屈服应力,εp为塑性变形量,εr为残余应变量,εf是应力为σf时试样的总变形量,εy是应力为σy时试样的变形量,即为弹性变形量Fig.1.The schematic diagram of tensile stress-strain curves for ferromagnetic materials:σfis the applied stress,σyis the yield stress of specimen,εpis the plastic deformation,εris the residual stress,εfis the total strain applied σyto the specimen, εyis the maxim of elastic deformation.
3 基于J-A理论的塑性变形磁化模型的修正
J-A理论包括两点基本假设∶1)材料磁化将不可逆地趋向理想的无磁滞磁化状态,即接近定理;2)材料的磁化可分为可逆磁化和不可逆磁化两部分.而J-A模型的关键包括三个方程∶无磁滞磁化强度方程、能量守恒方程以及等效磁场强度方程.
不同研究者建立模型时,相同物理量采用了不同符号表示,不方便读者比较.因此,为方便讨论,需将表示相同物理量的不同符号统一.具体如下∶Man为非磁滞磁化强度;Ms为饱和磁化强度,与材料的自身特性和温度有关;M为实际磁化强度,M=Mrev+Mirr;Mrev为可逆磁化强度,由畴壁弯曲引起;Mirr为不可逆磁化强度,由钉扎点阻碍磁畴移动引起;He为等效磁场强度,He=H+αM+Hσ;H为外磁场强度;Hσ为磁机械效应引起的等效磁场强度;σr为卸载后由残余塑性应变引起的残余应力;c为可逆磁化系数,衡量可逆磁化大小的标准,满足Mrev=c(Man−Mirr);δ为方向系数,dH/dt>0时,δ=1,dH/dt<0时,δ=−1,以保证钉扎点总是阻碍磁场变化;µ0为真空磁导率;a为形状系数,控制磁滞回线的形状;为均为与应力相关的材料系数,且为常数;Be为有效磁通密度,Be=µ0He.
3.1 对原塑性变形磁化模型表述的质疑
目前,已有多位研究者推导了塑性变形磁化模型,其中较为典型的模型如下.
1)Sablik建立的塑性变形磁化模型
在文献[10]中,在材料加载过程中,Sablik建立的塑性磁化模型为


而在文献[11]和[12]中,当材料产生塑性变形并卸载后,Sablik将等效应力磁场强度Hσ中加载应力σf换成了残余应力σr,即

其中,当外加磁场与应力方向相同时,σr=−σF;当外加磁场与应力方向垂直时,σr=vσF.
根据方程组(6),推导得出非磁滞磁化强度Man与磁化强度M关于外加磁场H的表达式∶
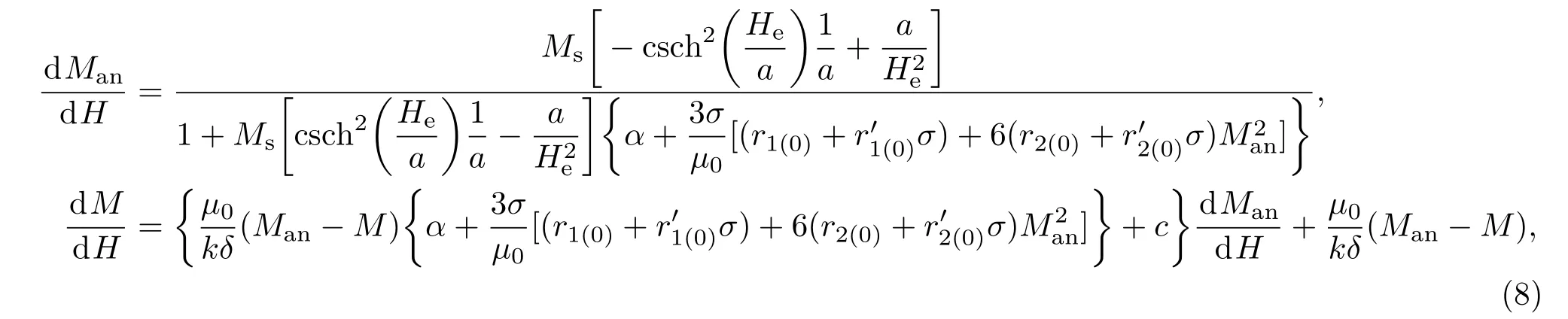
式中,σ泛指加载应力σf或残余应力σr.
2)Wang等[15]建立的塑性变形磁化模型
在文献[15]中,Wang等建立的塑性变形磁化模型为

式中,Hσp为塑性变形引起的等效磁场强度;Hσe为等效应力引起的等效磁场强度;σeq为Von-Mises等效应力;β为磁化强度与Von-Mises等效应力之间的夹角;为材料相关参数,为180°磁畴壁钉扎能量,m为磁矩.
3)Li等[16]建立的塑性变形磁化模型
在文献[16]中,Li等建立的塑性变形磁化模型为

式中,Hσr为残余应力引起的等效磁场强度.其推导的磁化强度M表达式为

4)Leng等[17]建立的塑性变形磁化模型
在文献[17]中,Leng等建立的塑性变形磁化模型为

式中,v′为应变相关系数,A为常数.其推导的磁化强度M的表达式为

通过梳理对比,发现上述模型存在将磁化强度M和无磁滞磁化强度Man混用、将不可逆磁化能量等效为全部的磁化能量、等效磁场强度中应力磁化项界定不清等问题,具体如下.
3.1.1 关于无磁滞磁化方程的表述
上述模型中,无磁滞磁化方程有两种形式,因此判断Man的哪一种表达式更合理十分必要.
在文献[10,11]中,Sablik等给出的无磁滞磁化曲线方程为
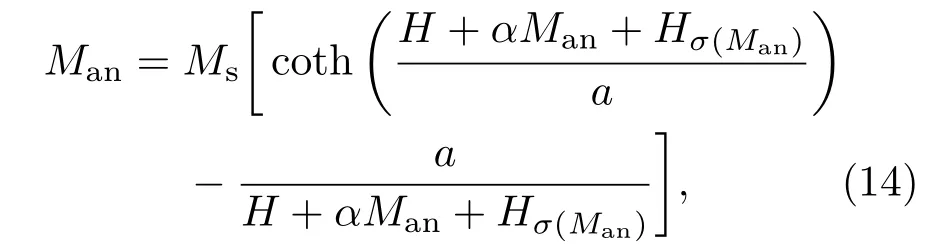
式中,Hσ(Man)表示Hσ与Man相关.
而文献[16,17]给出的无磁滞磁化曲线方程却为
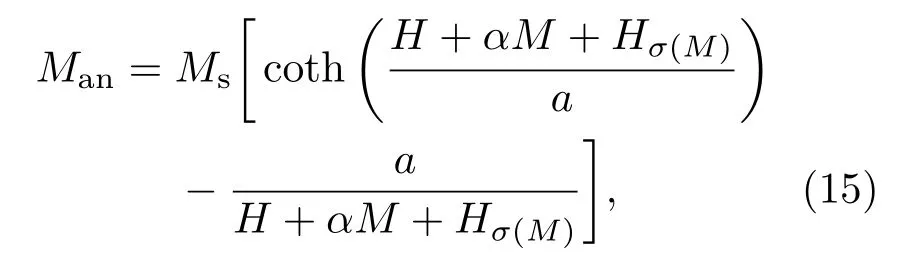
式中,Hσ(M)表示Hσ与M相关.
J-A理论采用改进的Langevin函数拟合各向同性材料的无磁滞磁化曲线,Langevin函数方程为L(x)=cothx−1/x,其具有以下性质∶当x趋近于0时,L(x)=0;当x趋于无穷大时,L(x)=1.同时,在没有外磁场的情况下,仅依靠应力作用,不能使金属磁化[19],即当H=0时,Hσ=0.由此∶当H=0时,Man=0,Hσ=0,若要使(H+αM+Hσ)/a趋于零,而α0,必有M趋于零,这与H=0时M=Mr(Mr为剩磁)相违背[2,20];而[H+αMan+Hσ(Man)]/a则能满足这一条件.因此,(15)式表述不合理,而(14)式表述合理.根据文献[14,21]的实验测试结果可知,当H足够大时,Man趋于Ms,即coth[(H+αMan+Hσ(Man)/a)]−a/[H+αMan+Hσ(Man)]趋于1,显然(14)式满足Langevin函数的基本性质,是拟合无磁滞磁化曲线的正确表述.
由此可见,(15)式在描述无磁滞磁化强度Man时采用了M,显然是将M和Man混用了,这将影响磁滞模型的准确性,而(14)式才是正确的.
3.1.2 关于能量守恒方程的表述
J-A理论是根据能量守恒原理推导而来,因此能量守恒方程的正确性至关重要.文献[2,3]给出的不可逆磁化过程能量守恒方程为
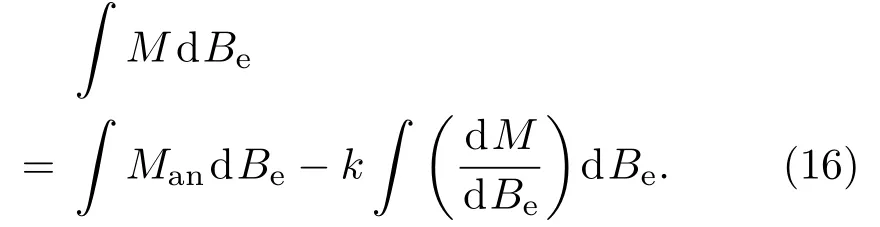
对(16)式进行微分得到∶
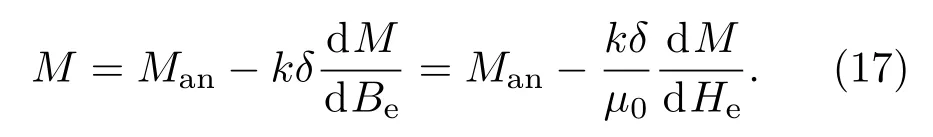
文献[4,6]给出能量守恒方程微分形式为

即

而文献[8]给出的能量守恒方程却为

即

由此可见,在J-A理论的经典文献中,针对能量守恒方程这一相同问题却有三种不同的表述,不同研究者在推导塑性变形磁化模型时也有不同引用∶文献[20,21]建立的模型引用了(17)式,而文献[11,12]却引用了(18)式.
对比(17),(18)和(21)式可知∶三个等式右边的物理意义为实际磁化能量等于无磁滞磁化能量减去实际磁化过程中的磁滞损耗能量,其中第一项为无磁滞磁化能量,第二项为实际磁化过程中的磁滞损耗能量.可以看出,上述等式关于无磁滞磁化能量的表述是一致的,而关于实际磁化过程中的磁滞损耗表述却各不相同.在实际磁化过程中,由于钉扎点存在,使磁畴壁移动受阻,导致磁滞损耗,而不可逆磁化分量Mirr即源于钉扎效应,因此磁滞损耗应与不可逆Mirr分量直接相关,而与可逆磁化Mrev无关,因此(17)式中关于磁滞损耗的表述不准确,而(18)式和(21)式中表述正确.但是(18)式等式左边表示磁化过程中不可逆的磁化能量只是实际磁化能量的一部分,而等式右边为实际磁化能量,存在部分与全部磁化能量之间的不匹配,从物理意义上可以断定其表述不准确.再者,(21)式中关于磁滞损耗的表达式中额外增加了(1−c)项,但并未清晰地给明其来历,且在利用He替换Be过程中存在问题.
根据上述分析,J-A理论在不同的文献中给出的数学表达式均存在不合理和矛盾之处,正确的能量守恒方程应为

对(22)式取微分可得

3.1.3 关于塑性变形磁化模型中的等效磁化强度表述
通过对比发现,不同研究者对塑性变形磁化模型中的等效磁场强度He表述也不相同∶Sablik在文献[10]中给出的等效应力磁场强度Hσ中的应力为加载时材料所受应力σf,如(6)式所示;但是其在文献[11]和[12]中定义的等效应力磁场强度Hσ中又采用了残余应力σr,如(7)式所示;此外,其等效磁场强度He中均采用的是无磁滞磁化强度Man.与Sablik在文献[11,12]中的表述相似,Leng等[17]亦将等效应力磁场强度Hσ中的应力考虑为残余应力σr,但σr=−v′A;同时,其等效磁场强度He中采用的是实际磁化强度M,如(12)式所示.在Wang等[15]建立的模型中,将等效应力磁场强度Hσ分为等效弹性变形磁场强度Hσe和等效塑性变形磁场强度Hσp两部分,即Hσ=Hσe+Hσp,同时,其等效磁场强度He中采用的是实际磁化强度M,如(9)式所示.Li等[16]建立的模型将Wang等[15]模型中的Hσe换成了由残余应力引起的等效磁场强度Hσr,如(10)式所示.
材料在塑性加载过程中或卸载后,加载应力σf或卸载后的残余应力σr是引起应力磁化的直接原因,因此等效应力磁场强度项Hσ中的应力考虑为σf或σr都可以.但(9)式和(10)式中额外增加了Hσp项,相当于重复考虑了塑性变形的影响;且(9)式中,Wang等将实际磁化强度M等效于非磁滞磁化强度Man,即M=Man=Ms[coth(He/a)−a/He],其计算结果也未出现磁滞现象(文献[15]中图2),存在问题.同时,对于He中应该采用非磁滞磁化强度Man,还是采用实际磁化强度M,上述文献也存在分歧.通过前述分析,作者认为应该将He作为两种情况考虑,即理想条件下的等效磁场强度He(Man)和实际条件下的等效磁场强度He(M).在非磁滞磁化方程中,由于将材料考虑为理想材料,不存在磁滞损耗,材料内部产生的磁化强度为非磁滞磁化强度Man,因此非磁滞条件下的等效磁场强度He(Man)中应采用Man;在实际磁滞磁化方程中,由于材料内部存在磁滞损耗,材料内部产生的磁化强度为M,因此在实际条件下的等效磁场强度He(M)中应采用M,如(24)式和(25)式所示.

式中,σ泛指加载应力σf或残余应力σr.在计算Man时应采用He(Man),而计算M时采用He(M).
3.2 塑性变形磁化模型的修正
如前所述,根据修正后的能量守恒原理,实际磁化的磁化能量等于无磁滞磁化能减去实际磁化过程中钉扎点造成的磁滞损耗,由此可得到更符合实际的磁化物理机制的能量表达式(23),将其整理后可得

再由M=Mrev+Mirr,Mrev=c(Man−Mirr)可得
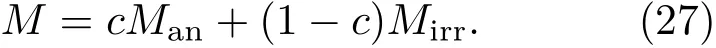
(27)式对H取微分可得
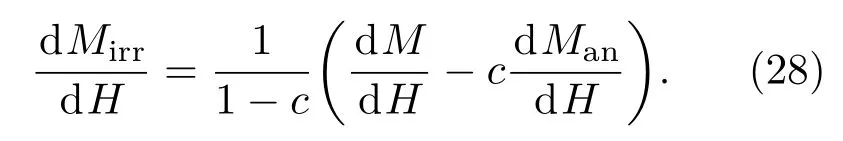
(25)式中He(M)对H取微分可得

联立(26),(28)和(29)式可得

则

由(31)式可得到

其中无磁滞磁化强度为
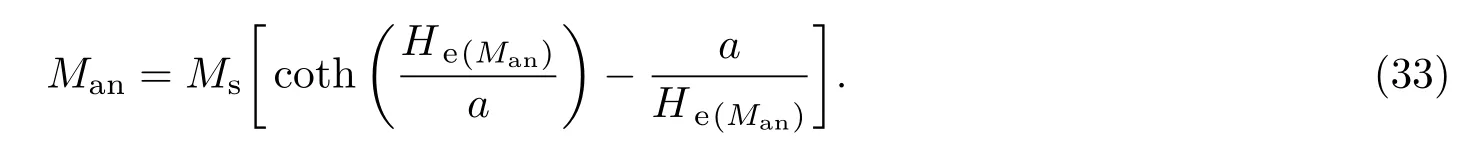
(24)和(33)式对H进行求导可得

由(34)式可得到

因此,联立(32)式和(35)式,即可计算得到M随外磁场强度H的变化曲线.
4 修正模型的数值分析及验证
为验证修正模型的改进情况,将修正模型计算结果与相关文献中的试验数据、现有模型计算结果进行对比.根据文献[2,10],相关参数取值如下∶µ0=4π×10−7N/A2,Ms=1.585×106A/m,α=8.44×10−6,r1(0)=7×10−18A−2·m2,=−1×10−25A−2·m2·Pa−1,r2(0)=−3.3×10−30A−4·m4,=2.1×10−38A−4·m4·Pa−1,c=0.25,G1=G3=0.81× 10−6m,G2=G4=3.8× 10−12m2,a0=600 A/m,k0/µ0=500 A/m,d=1×10−6m,C11=2.863×1011N/m2,C12=1.41×1011N/m2,A=2.5 × 1010J·m−3,q1=−2.15566× 10−4,q2=62.5447,q3=0.0618315,而杨氏模量Y及泊松比v均可根据C11,C12求得.
4.1 磁化强度曲线计算结果对比
当外磁场强度H=40 A/m,塑性变形εp=0—10%时,将修正模型计算得到的磁化强度曲线与文献[15]中图5、文献[16]中图4及文献[17]中图6进行对比,结果如图2所示.
由图2可知∶修正模型计算得到的磁化强度随塑性变形的变化趋势与文献[16]及文献[17]的计算结果趋势相似,而与文献[15]的计算结果相差较大∶在塑性变形初期,磁化强度即迅速下降;当塑性变形继续增大时,磁化强度随塑性变形的变化趋于平缓.但是,修正模型计算结果也有一定差别∶在塑性变形初始阶段,磁化强度下降趋势得更为剧烈,且随塑性变形增加更快地趋于平缓,平稳时的磁化强度值保持在1.3×105A/m左右,处于文献[16]和文献[17]的计算结果之间.
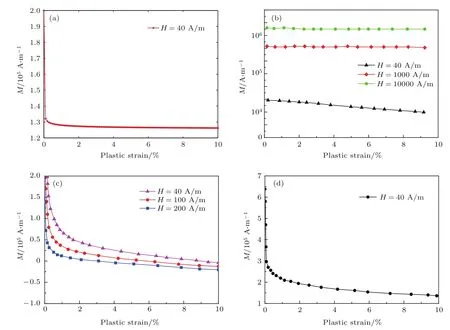
图2 (网刊彩色)恒定外磁场强度条件下磁化强度M随塑性变形εp变化曲线 (a)修正模型计算结果;(b)文献[15]中图5计算结果;(c)文献[16]中图4计算结果;(d)文献[17]中图6计算结果Fig.2.(color online)The comparison bettween the magnetization M versus plastic strain:(a)The magnetization by the modified magneto-plastic model;(b)the magnetization calculated in Ref.[15]Fig.5;(c)the magnetization calculated in Ref.[16]Fig.4;(d)the magnetization calculated in Ref.[17]Fig.6.
根据文献[16]中图6测量的试件表面漏磁场强度结果显示,与文献[15]计算结果相比,修正模型、文献[16]及文献[17]的磁化强度随塑性变形的变化趋势更符合试验结果.但是,由于其试验测试的表面漏磁场强度,而非试样本身的磁化强度,因此修正模型相对于文献[16]和文献[17]模型的改进情况,还需要进一步通过试验验证.
4.2 磁滞回线计算结果对比
当εp=0.001,0.002,0.003,0.004和0.005,外磁场强度H=−2.0×104—2.0×104A/m时,将修正模型计算得到的磁滞曲线与文献[10]中的图2(c)对比,结果如图3所示.

图3 (网刊彩色)磁滞回线计算结果对比 (a)修正模型计算结果;(b)文献[10]中图2(c)Sablik模型计算结果Fig.3.(color online)The comparison of the effective magnetic flux desity Beversus the applied field H:(a)The effective magnrtic flux Beby the modified model;(b)the effective magnrtic flux Beby the Sablik’s model in Ref.[10]Fig.2(c).
由图3可知∶1)修正模型计算结果的饱和磁通密度随塑性变形的增加而显著减小,而Sablik模型的饱和磁通密度随塑性变形的增加基本保持不变;2)Sablik模型计算结果显示,达到饱和磁通密度的外磁场强度随塑性变形的增大而显著增大,而修正后的模型该现象较弱;3)修正模型计算得到的剩余磁通密度Br随塑性变形的增大而减小,矫顽力Hc随塑性变形的增大而增大,而Sablik推导的模型计算得到的剩余磁通密度Br随塑性应变的增大基本保持不变,矫顽力随塑性变形的增大而增大.
由文献[22,23]中类似试验结果可知∶1)塑性变形使材料内部的钉扎点增多,磁滞损耗增大,饱和磁通密度会随塑性变形增大而减小;2)随塑性变形增加,试样达到饱和磁通密度的外磁场强度有增大趋势,但并没有Sablik模型计算结果那样剧烈;3)随着塑性变形增加,剩余磁通密度Br强度减小,而矫顽力Hc增大.因此,修正模型计算结果更符合试验现象.

图4 (网刊彩色)修正后模型计算结果与实验测试结果对比(a)修正后模型的计算结果;(b)文献[11]中原模型的计算结果Fig.4.(color online)The Comparison of the calculated results of the modified model and the experimental results:(a)The hysteresis loops given by the modified mode;(b)the hysteresis loops given by Sablik’s model in Ref.[11].
4.3 与相关试验数据的对比
以文献[23]图1(a)试验结果为例,对于含碳量为0.003%的试样,当εp=0时,a=390 A/m,k=275;当存在塑性变形时,取k0/µ0=200 A/m,a0=200 A/m,采用修正模型和文献[11]中原模型计算得到的磁滞曲线与实验结果进行对比,如图3所示∶与Sablik模型相比,修正模型的计算结果与实验数据符合更好,能够更真实地反映塑性变形对材料磁滞回线的影响.
5 结 论
本文根据磁化机理及能量守恒原理,指出了塑性变形磁化模型中的不合理之处,并在不改变J-A理论原有假设的基础上,推导得出了修正后的塑性变形磁化模型.通过与现有模型计算结果及相关试验结果对比,结果表明∶与现有模型相比,修正模型计算结果的饱和磁化强度和剩余磁化强度随塑性变形增加而减小,矫顽力随塑性变形增大而增大,达到饱和磁化强度时的外磁场强度随塑性变形增大而增大的趋势有所减弱,更符合试验结果,能更准确地模拟铁磁材料不同塑性变形条件下的磁滞回线变化情况.此外,计算过程中发现相关参数的取值对模型的计算精度有很大影响,后续研究可通过优化参数,提高修正模型计算结果的准确性.
[1]Li Z,Li Q M,Li C Y,Sun Q Q,Lou J 2011 Proc.Chin.Soc.Elect.Eng.31 124(in Chinese)[李贞,李庆民,李长云,孙秋芹,娄杰2011中国电机工程学报31 124]
[2]Jiles D C,Atherton D L 1984 J.Appl.Phys.55 2115
[3]Jiles D C,Atherton D L 1986 J.Magn.Magn.Mater.61 48
[4]Jiles D C 1992 IEEE Trans.Magn.28 27
[5]Jiles D C,Thoelke J B 1989 IEEE Trans.Magn.25 3928
[6]Sablik M J,Jiles D C 1993 IEEE Trans.Magn.29 2113
[7]Jiles D C 1995 J.Appl.Phys.28 1537
[8]Jiles D C 1994 J.Appl.Phys.76 5849
[9]Jiles D C,Li L 2004 J.Appl.Phys.95 7058
[10]Sablik M J 2004 IEEE Trans.Magn.40 3219
[11]Sablik M J,Geerts W J,Smith K,Gregory A,Moore C 2010 IEEE Trans.Magn.46 491
[12]Sablik M J,LandgraffJ G,Paolo S Comparing grain size and dislocation density effects for hysteresis loops with the same maximumflux density in a magnetic hysteresis model https://wwwresearchgatenet/publication/265264412[2017-03-08]
[13]Sablik M J,Rios S,LandgraffJ G 2005 J.Appl.Phys.97 10E518
[14]Suliga M,Borowik L,Chwastek K 2015 Arch.Metall.Mater.60 409
[15]Wang Z D,Deng B,Yao K 2011 J.Appl.Phys.109 083928
[16]Li J W,Xu M Q,Leng J C,Xu M X 2012 J.Appl.Phys.111 063909
[17]Leng J C,Liu Y,Zhou G Q 2013 NDT&E Int.55 42
[18]Jiang P,Wang W 2009 Fundamentals of Engineering Mechanics(II):Mechanics of Materials(Beijing:Higher Education Press)pp61–63(in Chinese)[蒋平,王维 2009工程力学基础(II):材料力学(北京:高等教育出版社)第61—63页].
[19]Doubov A A K V G 2001 Proceedings of the Second International Conference“Diagnostics of the Equipment and Constructions with Usage of Metal Magnetic Memory” Moscow,Russia,February 26–28,2001 p1
[20]Jiles D C 2000 J.Appl.Phys.21 1196
[21]Makar J M,Tanner B K 1998 J.Magn.Magn.Mater.184 193
[22]Iordache V E,Hug E,Buiron N 2003 Mat.Sci.Eng.AStruct.359 62
[23]Makar J M,Tanner B K 2000 J.Magn.Magn.Mater.222 291
PACS∶75.80.+q,62.20.f—,75.30.Cr,75.60.EjDOI∶10.7498/aps.66.107501
*Project supported by the Major Program of Sichuan Province Science and Technology Plan,China(Grant No.2015SZ0010),the Key Technology Research and Development Program of Sichuan Province,China(Grant No.2013GZ0150),and the Scientific Research Foundation of Sichuan Province,China(Grant No.2014GZ0121).
†Corresponding author.E-mail:402585133@qq.com
Modeling plastic deformation effect on the hysteresis loops of ferromagnetic materials based on modified Jiles-Atherton model∗
Liu Qing-You1)2)Luo Xu1)†Zhu Hai-Yan3)Han Yi-Wei1)Liu Jian-Xun1)
1)(Schoolof Mechatronic Engineering of Southwest Petroleum University,Chengdu 610500,China)
2)(Key Laboratory of Fluid and Power Machinery of Xihua University,Ministry of Education,Chengdu 610039,China)
3)(College of petroleum engineering of Southwest Petroleum University,Chengdu 610500,China)
10 October 2016;revised manuscript
10 March 2017)
Plastic deformation is one of the most important features that affect the hysteresis magnetic properties of steels,because it changes the dislocation density and affects domain-wall movement and pinning.In order to model the effect of plastic deformation on the magnetic properties,the prevailing Jiles-Atherton(J-A)theory is extensively used.However,the J-A models in a series of papers published by Jiles et al.are not completely consistent.As a result,there exists no uniform formula of magneto-plastic model established by different researchers,based on different J-A models,and various versions given by different mathematic expressions of magneto-plastic modeloften create difficulty in discriminating the accuracies and effectivenesses of the analyzed results.Therefore,it is necessary to establish an accurate and reasonable magneto-plastic model.In this paper,on the basis of magnetization mechanism of ferrimagnet and plastic deformation model,the effects of plastic deformation on the magnetic characteristic parameters adopted in magneto-plastic model,such as dislocation density,pinning coefficient and scaling constant,are analyzed and the relationship between them is first established.Then,by contrasting the fitting formula of the anhysteretic magnetization curve,the energy conservation equation and the effective magnetic field equation established by different researchers,several queries are proposed,and the irrationality and inaccuracy of the existing magneto-plastic model are elucidated,such as the mixing of anhysteresis magnetization and magnetization,the unreasonably regarding the irreversible magnetization energy as actual total magnetization energy.Thus,the energy conservation equation,the effective magnetic field equation and the anhysteretic magnetization equation are modified,and the differential expression of the magneto-plastic model is re-derivedfinally.Comparing the results calculated by the existing magneto-plastic models with the experimental results,it is seen indeed that a more sharp change of magnetization appears at small plastic deformation,then,the values of magnetization decrease more slowly with the increase of plastic deformation than those from the models respectively proposed by LiJian-Wei,Leng Jian-Cheng and Wang Zheng-Dao;the saturation magnetization and residual magnetization decrease with the increase of plastic deformation,the coercive force is increased oppositely and the trend to reach the saturation magnetization becomes gentler,which is more exactly consonant with experiment observation than that calculated by the Sablik’s model;additionally,the hysteresis loops of the plastically deformed carbon-steel samples calculated by the modified magneto-plastic model are also in better agreement with the experimental results than those from the existing models.Consequently,the modification is effective,and the modified magneto-plastic model is more accurate to simulate the plastic deformation effect on the magnetic property of ferromagnetic material.
∶Jiles-Atherton model,hysteresis loop,magneto-plastic model,magneto-mechanical effect
∗四川省科技计划重大项目(批准号:2015SZ0010)、四川省科技支撑计划(批准号:2013GZ0150)和四川省科技计划项目(批准号:2014GZ0121)资助的课题.
†通信作者.E-mail:402585133@qq.com
©2017中国物理学会Chinese Physical Society

