梯度倾斜相关测量水平C和横向风速廓线的理论与仿真研究∗

彭哲靖旭 侯再红 吴毅

1)(中国科学技术大学环境科学与光电子技术学院,合肥 230026)

2)(中国科学院安徽光学精密机械研究所,中国科学院大气成分与光学重点实验室,合肥 230031)

彭哲1)2)靖旭2)†侯再红2)吴毅2)

1)(中国科学技术大学环境科学与光电子技术学院,合肥 230026)

2)(中国科学院安徽光学精密机械研究所,中国科学院大气成分与光学重点实验室,合肥 230031)

(2016年12月1日收到;2017年3月8日收到修改稿)

根据Rytov近似以及泰勒湍流冻结假设,推导出以不同距离的前向散射光为信标的水平路径上梯度倾斜角的相关表达式.基于该表达式,在理论上提出了计算湍流强度与横向风速的新方法,并通过数值仿真对该方法进行了初步验证.结果表明,在5%高斯误差情况下,大气折射结构常数和风速的计算结果与理论真值在整体变化上具有较好的一致性,线性相关系数分别能达到0.8与0.9.该方法能够得到不同湍流与风速条件下的湍流强度廓线以及风速廓线,为反演大气湍流强度以及风速提供了一种新思路.

∶梯度倾斜,相关,大气湍流,风速

PACS∶42.68.—w,42.68.Bz,42.25.DdDOI∶10.7498/aps.66.104207

1 引 言

光在大气中传播会由于大气湍流的影响而产生随机相位抖动和光强起伏,严重影响了天文观测以及激光工程的应用.而湍流折射率结构常数C(h)以及风速v(h)则是与大气湍流相关的重要参数.自适应光学系统能够实时校正大气湍流的影响,但是其校正能力受湍流的时间特征频率的影响,实时获取湍流特征频率需要知道大气风场和湍流强度廓线.因此,实时获取大气湍流廓线以及风速廓线对光在大气中传播具有重要意义.

目前,测量大气湍流廓线的方法有探空气球法[1]、星光法[2,3]和激光雷达法[4−7].探空气球法操作简单,但容易受到风的影响,实时性不高.星光法,如SCIDAR(SCIntillation Detection And Ranging),PML(Profiler of Moon Limb)等,有较好的实时性和精度,但容易受天气的影响.激光雷达法能够测量各种不同路径上的湍流廓线,其测量结果的空间分辨率与仪器自身的空间分辨率相关.测量风速廓线的方法有探空气球、微波测风雷达、基于多普勒效应的风廓线雷达、基于抖动和闪烁的激光雷达[8,9].探空气球测量简单,成本低,但测量周期长,实时性不高.微波测风雷达技术成熟,受天气影响较小,但回波信号在大气干燥时偏弱.利用多普勒效应测风精度高,一般采用法布里标准具,受温度影响较大,且其成本高.基于抖动和闪烁的激光雷达方法大多都是测量路径上的平均风速,想要获取风速廓线通常需要模型假设.

本文采用激光雷达的方法,通过质心偏移得到梯度(G)倾斜角相关特性,并利用矩阵变换与近似的方法获取水平湍流强度廓线和风速廓线.该方法是对现有激光雷达方法对C测量的补充,以及对风速随路径分布测量的改进.该方法具有较好的实时性,且可以实现不同路径上的测量.

2 理论推导

如图1所示,以图中z轴所示方向为正方向,O为坐标原点.将S(source z=L0)处的激光器产生的激光在不同距离上的前向散射光作为信标光(图中F处),并在O处用双孔望远镜采用傍轴方式接收该激光的前向散射,通过在两孔前安装有一定楔角的楔镜和在焦平面倾斜安装电荷耦合器(CCD),激光信号就能在倾斜的焦平面成像为两条光柱[5,10].

对光柱上对应F(forwad scattering z=L)处的前向散射有

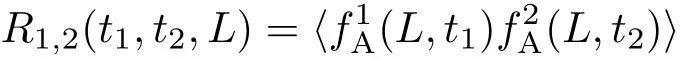
其中Ri,j(t1,t2,L)表示孔径i(i=1,2)在t1时刻与孔径j(j=1,2)在t2时刻接收到的质心抖动相关.从S到F段,同一时刻,激光自身的质心抖动以及传输路径上的质心抖动对两个孔径而言都是一样的,故有(L,t)=(L,t).

梯度倾斜(G倾斜)即平均光线方向,与孔径的平均相位梯度相关[11].实际测量中,G倾斜角可由质心在CCD靶面上的偏移与成像焦距之比求得.故质心抖动相关与G倾斜角相关呈正比关系,比值与焦距有关.由Rytov近似以及泰勒湍流冻结理论,有[9−13]

图1 测量原理图Fig.1.Sketch map of measurement.

其中k0为波数,z表示到望远镜的距离,κ表示空间波数,Φ(κ,z)表示湍流谱分布,γ=1−z/L表示传播因子,余弦函数对应相位抖动的衍射因子,J0表示第一类零阶贝塞尔函数,τ表示t1与t2的时间差,F(γκ)表示滤波函数.相对于探测孔径,光源扩展度远小于衍射极限,因而可不考虑光源的滤波函数,即F(γκ)仅包含孔径滤波函数.对应的孔径滤波函数[11,13]可表示为

其中D表示孔径直径,J1为第一类一阶贝塞尔函数.

而对于Kolmogorov湍流,有

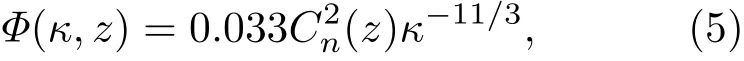
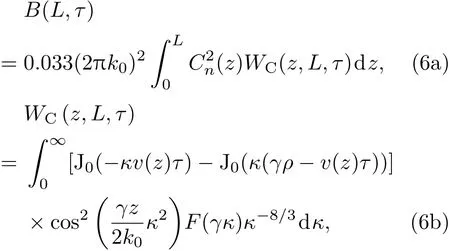
其中B(L,τ)即为求解湍流折射率结构常数以及风速所需相关量,它对应于单个孔径G倾斜角的自相关与两个孔径G倾斜角的互相关之差;WC(z,L,τ)表示对应的湍流折射率结构常数的权重.由(6a)式以及(2a)和(2b)式可知,B(L,τ)不受光源自身质心抖动以及S到F段质心抖动影响.根据B(L,0)以及WC(z,L,0)即可通过合适的算法求解得到湍流强度沿路径的分布.为了得到风速,可以通过求解B(L,τ)在τ=0时刻的导数.求导可得

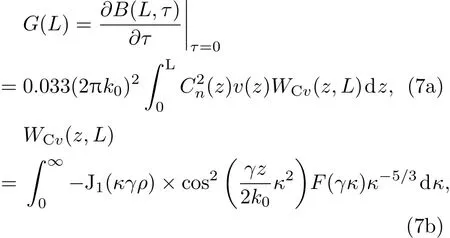
其中,G(L)为B(L,τ)在τ=0时刻的导数,WCv(z,L)为湍流折射率结构常数与风速乘积的权重.通过联立(6a)和(6b)以及(7a)和(7b)式,可求解得到风速随路径的分布.而事实上对时间求导通常需要较高的时间分辨率,对于一个200 Hz的CCD,在不考虑外来误差影响的情况下,通过泰勒展开求取导数,其相对误差不会超过1.5%.

若以后向散射作为信标光,则后向散射光(从信标光到望远镜)和原始激光(从激光器到信标光)会存在一定的相关性,并不能认为是零.若要计算风速与则需要消除该相关性所带来的影响.可以通过差分的手段消除原始激光带来的影响,进而进行相关与求导运算得到与风速的相关表达式及权重函数.

3 算法原理

在不考虑盲区影响的情况下,我们将O(z=0处)到S(z=L0处)看作n段,即l1l2···ln,第一段为l0→ l1,第n段为ln−1→ ln,其中l0=0.并认为每一段的风速与都保持不变,即v1v2···vn与表示第i段的风速,表示第i段的湍流折射率结构常数.令

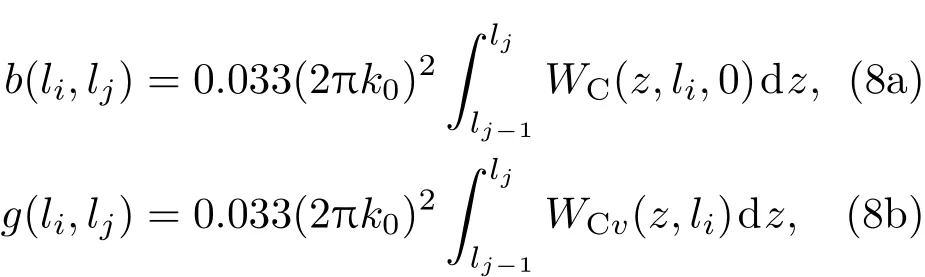
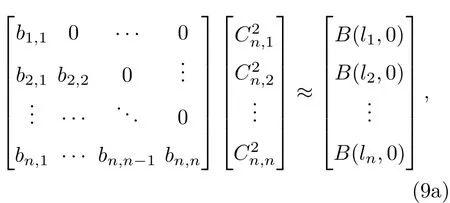
其中B(li,0)表示将li处的前向散射光作为信标光且时间差为时的差分相关量,G(li)对应B(li,τ)在τ=0时的导数.当孔径间距、孔径直径以及激光波长已知,即可计算得到bi,j与gi,j.对于(9a)与(9b)式,直接通过最小二乘法求解会导致很大误差.因为矩阵本身是病态的,同时误差的存在会导致最优解并不是我们想要的结果,往往要加以约束.

取接收孔径间距ρ=0.235 m,孔径直径D=0.12 m,激光波长λ=532 nm,对于不同的L,两权重函数的曲线如图2所示

图2 (网刊彩色)权重随距离z的变化曲线 (a)WC的变化曲线;(b)WCv的变化曲线Fig.2.(color online)The variation of weight function with z(a)variation of WC;(b)variation of WCv.

从图2可以看出,当z接近L时,即γ接近0时,权重在量级上快速减小.权重的这种快速下降正是导致矩阵病态的原因.由于这部分权重在量级上远小于其他部分,因而可以近似认为其值为0.基于这一点,并根据每个分段内权重曲线变化特性对上述矩阵进行近似变换可以得到

α和β为与每一段上曲线变化相关的量.

4 数值仿真结果与分析

为便于计算,我们将距离间隔设置为固定值50 m.而实际测量时,空间分辨率会随着传播距离的增加逐渐降低,要得到50 m间隔的相关量,可先对实际观测结果进行降噪拟合,然后对所得曲线进行间隔为50 m的采样.同时由于上述各种近似都会引入误差,随着误差传递,当累积到一定程度时,则需要增大分段间距以降低该误差带来的影响.我们取L0=4000 m,此时,在50 m的分段间距下,近似误差给计算带来的影响很小.

而实际上误差总是存在的.若每一帧的光柱抖动都含有方差5%的高斯噪声,则对计算得到的B以及通过泰勒展开得到的G进行多帧平均,并对其进行小波降噪和多项式拟合,得到结果如图4所示.

从图4可以看出计算得到的结果与设定值有着相同的变化趋势,但在细节变化上有所丢失,这是降噪以及拟合的平滑效果所致,同时也是由于抖动对的不敏感性.的最大对数相对误差不超过3.4%,平均对数相对误差不超过0.9%,风速的最大绝对误差不超过1.82 m/s,平均绝对误差不超过0.47 m/s.当湍流与风速条件发生变化时,依然有类似的结果,如图5所示.

图5(b)给出的风速结果误差较大,是由于当风速存在方向变化且变化较快时,多项式拟合误差相对较大.两组计算结果一定程度上验证了该方法在理论上的可行性,更深入的研究需要进一步的实验验证.

图3 (网刊彩色)不考虑误差的情况下设定值与计算值的对比 (a)的对比;(b)风速的对比Fig.3.(color online)Comparison between the set value and the calculated value regardless of errors(a)comparison of ,(b)comparison of wind velocity.

图4 (网刊彩色)考虑误差的情况下设定值与计算值的对比 (a)的对比;(b)风速的对比Fig.4.(color online)Comparison between the set value and the calculated value considering errors(a)comparison of ,(b)comparison of wind velocity.

图5 (网刊彩色)湍流与风速条件发生变化时设定值与计算值的对比 (a)的对比;(b)风速的对比Fig.5.(color online)Comparison between the set value and the calculated value within change of turbulence and wind(a)comparison of ,(b)comparison of wind velocity.

5 结论与讨论

本文基于数值仿真提出了一种基于G倾斜角相关测量水平横向风速和湍流强度的方法.由于以后向散射光作为信标光测量风速系统较为复杂,因而采用前向散射光作为信标光,并根据统计与相关理论,推导出了相关抖动与湍流强度以及风速之间的表达式,最终通过矩阵变换与近似来实现湍流强度与风速的计算.

仿真结果表明,对于水平测量,在不考虑盲区或盲区较小且不考虑光束扩展的情况下,该方法能有效地反演出横向风速与湍流强度随路径的变化,而不仅仅只是路径上的一个平均量,且不依赖于模型假设.该方法仍需要通过实验来进行验证,并通过改进扩展以实现垂直方向的反演.

[1]Vernin J,Munoz-Tunon C 1994 Astron.Astrophys.284 311

[2]Avila R,Cuevas S 2009 Opt.Express 17 10926

[3]Ziad A,Blary F,Borgnino J,Fanteï-Caujolle Y,Aristidi E,Martin F,Lantéri H,Douet R,Bondoux E,Mékarnia D 2013 Astron.Astrophys.559 L6

[4]Cheng Z,TanfF,Jing X,He F,Hou Z H 2016 Acta Phys.Sin.65 074205(in Chinese)[程知,谭逢富,靖旭,何枫,侯再红2016物理学报65 074205]

[5]Jing X,Hou Z H,Wu Y,Qin L A,He F,TanfF 2013 Opt.Lett.38 3445

[6]Cui C L,Huang H H,Mei H P,Zhu W Y,Rao R Z 2013 High Power Laser Part.Beams 25 1091(in Chinese)[崔朝龙,黄宏华,梅海平,朱文越,饶瑞中 2013强激光与粒子束25 1091]

[7]Cheng Z,He F,Jing X,TanfF,Hou Z H 2016 Acta Opt.Sin.36 401004(in Chinese)[程知,何枫,靖旭,谭逢富,侯再红2016光学学报36 401004]

[8]Tichkule S,Muschinski A 2012 Appl.Opt.51 5272

[9]Schock M,Spillar E J 1998 Opt.Lett.23 150

[10]Jing X,Hou Z H,Qin L A,He F,Wu Y 2011 Infrared Laser Eng.40 1352(in Chinese)[靖旭,侯再红,秦来安,何峰,吴毅2011红外与激光工程40 1352]

[11]Sasiela R J 2007 Electromagnetic Wave Propagation in Turbulence:Evaluation and Application of Mellin Transforms(Bellingham:SPIE)pp69–102

[12]Wang T,Clifford S F,Ochs G R 1974 Appl.Opt.13 2602

[13]Rao R Z 2012 Modern Atmospheric Optics(Beijing:Science Press)pp368–433(in Chinese)[饶瑞中 2012现代大气光学 (北京:科学出版社)第368—433页]

[14]Cai D M,Ti P P,Jia P,Wang D,Liu J X 2015 Acta Phys.Sin.64 224217(in Chinese)[蔡冬梅,遆培培,贾鹏,王东,刘建霞2015物理学报64 224217]

[15]Guo Y M,Ma X Y,Rao C H 2014 Acta Phys.Sin.63 069502(in Chinese)[郭友明,马晓燠,饶长辉2014物理学报63 069502]

[16]Huang K T 2014 Ph.D.Dissertation(Hefei:Hefei Institutes of Physical Science,the Chinese Academy of Sciences)(in Chinese)[黄克涛 2006博士学位论文(合肥:中国科学院合肥物质科学研究院)]

PACS∶42.68.—w,42.68.Bz,42.25.DdDOI∶10.7498/aps.66.104207

*Project supported by the National Natural Science Foundation of China(Grant No.41405014).

†Corresponding author.E-mail:xujing@aiofm.ac.cn

Simulation research and theoretical study on measurement of atmospheric optical turbulence and wind profile using the correlation of gradient-tilt∗

Peng Zhe1)2)Jing Xu2)†Hou Zai-Hong2)Wu Yi2)
1)(Department of Environmental Science and Optoelectronic Technology,University of Science and Technology of China,Hefei 230026,China)
2)(Key Laboratory of Atmospheric Composition and Optical Radiation,Anhui Institute of Optics and Fine Mechanics,Chinese Academy of Sciences,Hefei 230031,China)

1 December 2016;revised manuscript

8 March 2017)

In this article,a theoretical method based on thefluctuation of gradient tilt(G-tilt)of active light source is proposed to estimate the horizontal profiles of atmospheric optical turbulence()and transverse wind.The G-tilt,related to the average phase gradient,is in the same direction as the average ray direction.And G-tilt angle is considered to be equal to the ratio between the centroid position offset and the focal length.In this method,a theoretical model based on lidar system is set up,in which forward scatter light beams at different distances are taken as beacons.These beacons are detected by a two-aperture telescope.And two light columns,from which we can obtain the information about G-tilt angle,are imaged by these beacons.In order to obtain the turbulence intensity and wind velocity from G-tilt angle with our theoretical model,the differential cross-correlation expressions of G-tilt angle and its derivative are derived in detail.These two expressions are based on the spatial cross-correlation function obtained from Rytov approximation and Taylor’s frozen- flow hypothesis for Kolmogorov turbulence.Simultaneously,path weighting functions ofand wind velocity are derived,and the effects of path weighting functions on the calculation of our method are analyzed.Based on such an analysis,to realize the inversion of turbulence intensity and transverse wind,the matrix transformation algorithm is proposed.We ignore some minimal values of the path weighting functions in our algorithm so that the ill-conditioned matrix is avoided.Besides,numerical simulation is used for preliminarily validating this method.In our simulation,varies randomly between 10−15m−2/3and 10−14m−2/3while wind velocity ranges from −5 m/s to 10 m/s.The sign of the wind velocity represents the direction of wind.According to the simulation results,the horizontal profiles of atmospheric optical turbulence and transverse wind calculated are consistent with their theoretical values no matter whether there exists Gaussian noise.When the ratio between the standard deviation of Gaussian noise we added and the original signal is 0.2,the maximum relative error of logarithmicis 3.4%,and the correlation coefficient between the calculated results and theoretical values foris 0.8.Besides,the maximum absolute error of wind velocity is 1.82 m/s,and the correlation coefficient between the calculated results and theoretical values for wind velocity is 0.9.Even if the horizontal profiles of atmospheric optical turbulence and transverse wind vary largely,the calculation results of our method remain stable.Therefore,a new idea is provided for measuring atmospheric turbulence and wind.

∶gradient-tilt,correlation,atmospheric turbulence,wind velocity

∗国家自然科学基金(批准号:41405014)资助的课题.

†通信作者.E-mail:xujing@aiofm.ac.cn

©2017中国物理学会Chinese Physical Society