土石坝饱和—非饱和稳定渗流场影响分析

韩 雪

(通河县水务技术服务中心，黑龙江 通河 150900)



土石坝饱和—非饱和稳定渗流场影响分析

韩 雪

(通河县水务技术服务中心，黑龙江 通河 150900)

土石坝是当今最为常用的一种坝型，而防渗体系的构建对坝体稳定具有十分重要的作用，国内外的多起水利工程安全事故足以引起足够的重视。进行土石坝的渗流分析需要将渗流场定义为饱和和非饱和区的共同体，过去的经验已然证明二者的相辅相成。二者相比非饱和渗流的运动特性相对复杂，影响因子也较饱和渗流多。文章结合工程实例，运用有限元数值模拟出土石坝在饱和与非饱和渗流中渗流场的变化规律，得出正确合理的渗流场理论，研究成果在土石坝的防渗体系的构建上具有一定的参考价值。

土石坝；非饱和土；渗流；有限元

0 前 言

非饱和土是指经开挖、重塑和碾压密实的土体。土石坝土体介质的非饱和特性至今依然是现代水利工程界的热门课题[1]。因为其不仅广泛存在于水利工程，农业领域也运用广泛，如地下水位变化、土体水份渗透及蒸发等的变化对地下水的影响，其主要作用在土体的非饱和区域。在土木工程领域，雨水的渗透对地基稳定性的影响也要分析饱和-非饱和的渗流分布规律。

土石坝的渗流场由饱和区和非饱和区共同组成[1]，二者相互制约又相互联系。影响因素诸多，降雨量、水位的变化等均能改变饱和区和非饱和区的作用区域，理论上单独对非饱和区的渗流研究更能反映工程实际，假如单独进行饱和区的渗流分析，直接加大了计算难度，伴随着有时计算陷入死循环难以求解。

影响非饱和渗流运动的因素众多，且形态也较复杂，比如固、液、气三种不同形态、温度、体积比、压强和空气压力等，从力学角度范畴将这是多因子相互作用的共同结果，也是相互耦合的受力变化过程。目前国内随着多年的研究发现，对于非饱和渗流参数的确定至关重要，参数的确定才能计算分析得出非饱和渗流的渗流场分布规律[2]。为使更加密切联系工程实际，并为工程设计运行提供正确合理的理论依据，足以见土石坝饱和-非饱和渗流场的数值模拟分析的重要性。

1 饱和-非饱和渗流有限元解法

1.1 定解条件

对稳定渗流方程进行求解时，列出边界条件；对非稳定渗流方程求解时，列出初始条件和全过程的边界条件[3]。

基于流动的数学模型，可分为3类边界条件：

1)第1类边界条件是水头边界条件，假定已知边界的水头分布。表达式如下：

h|Γ1=H1(x,y,z,t)

(1)

2)第2类边界条件是流量边界条件，假定已知边界的位势函数，表达式如下：

(2)

3)第3类边界条件是混合边界条件，定义边界外水头差和水位能量呈线性关系，即：

(3)

式中：α、β为正常数。

1.2 饱和-非饱和渗流的基本微分方程

在非饱和土体中，通常孔隙流体组成部分有水和气，假定只考虑流水作用，结合达西定律和水体积变化值，建立非饱和渗流基本微分方程[4]，即：

(4)

假定总应力对时间导数为零，孔隙气压力同理，则上式表达为：

(5)

式中：m2w为坝基水的黏滞力变化下体积系数。可将式(4)变为

(6)

若假设是稳定渗流分析，即：

(7)

非饱和与饱和土体的在渗流方程表达式上虽相同，但非饱和渗透系数为变值，作用点变化，系数随之改变。将上式展开，得出基本的非线性方程表达式如下：

(8)

1.3 饱和-非饱和渗流的有限元解法

国内目前对土体饱和与非饱和渗流的研究公式主要是运用Galerkin加权余量法，推导出二维有限元饱和-非饱和渗流问题公式，具体推导过程如下[3]：

首先已知近似解假定一个试探函数，列出加权余量方程，基于格林原理的方法消除二次微分，并将所得式代入假定函数及边界条件，进而得出组合渗透矩阵，推导得到参数矩阵。以单元形式表达如下：

∫A[B]T[K][B]dA×{Hi}e+∫A[N]Tλ[N]dA

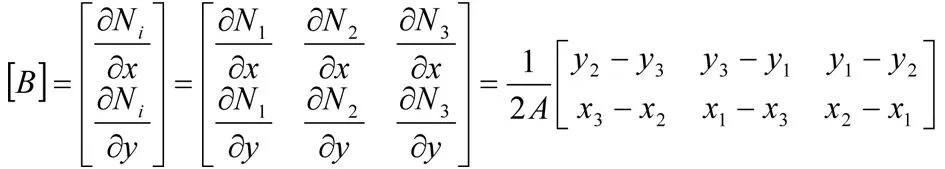
(9)

数值积分后得出：

(10)

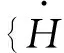
在时间微分的处理中首先计算出特定时间的节点水头，再利用有限差分法继续求解[5]。得出的各单元数值代入式(5)，进而得出总体流动方程组。要求各单元各节点具有相似性，水头必须保持一致。下面对各节点处的水头{H}求解过程需依据总体流动方程组。各节点处的水头值直接影响渗透系数，采用迭代法来实现。文章基于SEEP程序采用向后差分法进行迭代，在运算中设置容许误差和迭代次数上限。该程序通过求解得出的节点收敛水头值，进而计算得到渗流速度和孔隙水压力。

2 工程实例

建于中国西南地区的某均质土坝，主要功能是调蓄和灌溉，兼以发电功能，大坝坝顶长度505.0m，坝顶高程854.0m，最大坝高68.0m。上、下游坝坡比为1∶3、1∶2.75。该坝的最大横剖面图如图1所示[6]。大坝内排水为水平褥垫方式。基岩上部为强风化层，基岩下部岩体为相对隔水层。

图1 大坝横剖面图

2.1 有限元模型与计算参数

坐标系定义如下：X轴为顺河流方向上游指向下游为正；Y轴是竖直方向，指向向上为正，有限元网格剖分图如图2。

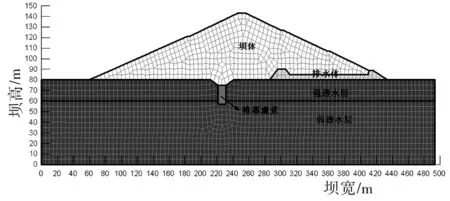
图2 大坝有限元模型

模型的计算区域范围选取：沿河流方向分别向上、下游各取68m；竖直方向从坝基向下取80m。

有限元网格划分：该模型由颜色各异的5个分区组成，分别表示大坝、强弱透水地层、防渗帷幕和下游排水体五部分。计算软件采用GeoStudio，模块为SEEP/W。该模块的特点是适用性强，能够自动剖分单元，模型划分单元选取三角形和四边形单元，这样划分很大程度上能提高计算准确度。网格剖分后共生成单元2113个，结点2245个。

对大坝各分区材料进行了力学实验，并结合类似工程实例检测结果，该土石坝的各物理力学参数见表1[7]。

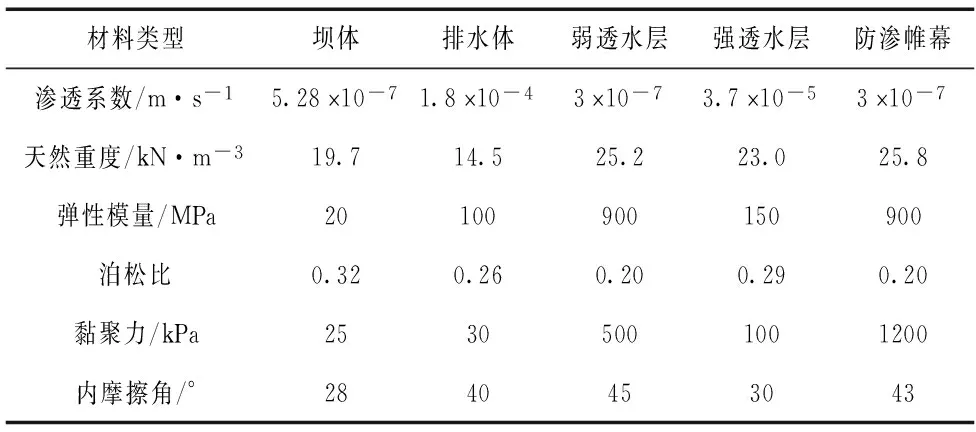
表1 土石坝各分区材料物理力学参数表

2.2 稳定渗流场对比分析

文章研究情况为正常工况下的稳定渗流场。定义边界条件如下：坝基处认定为不透水边界，即渗流量为零；在坝体上游面和左侧强透水层高程定义总水头145m，在坝体下游面定义总水头94m，将上、下游的总水头值定义为水头边界。

2.2.1 饱和稳定渗流场

定义材料类型：在运用SEEP/W软件[8]分析时，将大坝的各分区材料渗透系数定义为饱和渗透的。

通过有限元计算分析，饱和稳定渗流场在正常工况下的总水头、压力水头、孔隙水压力分布图及计算结果已得出工况下的浸润线见图3-5。

图3 正常工况下饱和稳定渗流场总水头等值线分布图

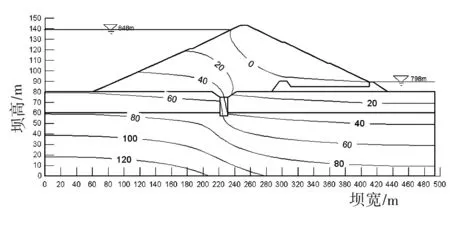
图4 正常工况下饱和稳定渗流场压力水头等值线分布图

图5 正常工况下饱和稳定渗流场孔隙水压力等值线分布图

2.2.2 饱和-非饱稳定渗流场

定义材料类型：根据以往浸润线作为饱和-非饱和的分界线，结合工程实际定义大坝材料为非饱和状态下的参数，其他4分区材料定义为饱和状态下的材料参数。

通过有限元计算分析可得到饱和-非饱和稳定渗流场的总水头、压力水头、孔隙水压力分布图见图6-8。

2.2.3 饱和与饱和-非饱和稳定渗流场对比分析

对比分析图3和图6，大坝下游的浸润线高度在非饱和稳定渗流场中和饱和时相比偏低。分析原因在饱和稳定渗流分析时，理论认为浸润线位置处无水能的损失，仅为渗流场的分界线；在非饱和稳定渗流场分析影响时，水量从上向下由饱和区进入非饱和区，原因是非饱和区的基质吸引力造成的，这样使得非饱和渗流的浸润线高度降低，压力水头下降，由此带来水头损失的增加。

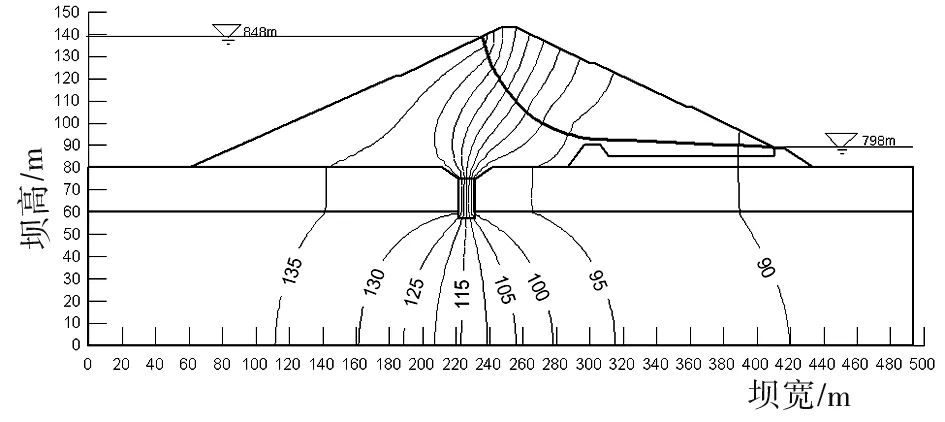
图6 饱和-非饱和稳定渗流场总水头等值线分布图

图7 饱和-非饱和稳定渗流场压力水头等值线分布图

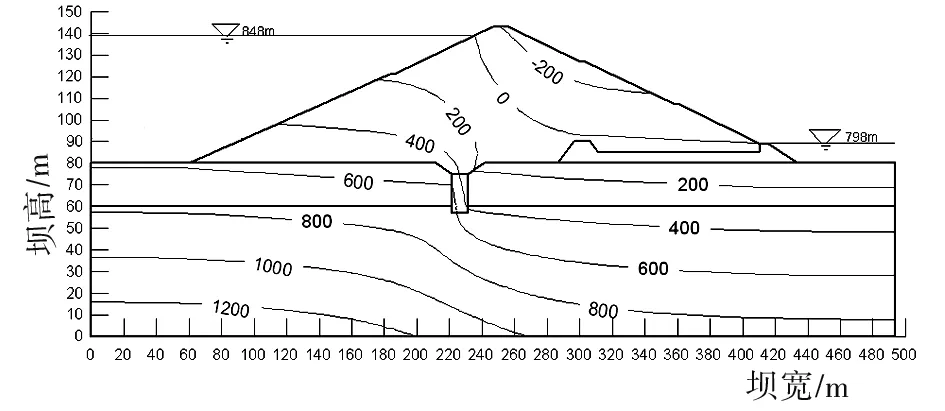
图8 饱和-非饱和稳定渗流场孔隙水压力等值线分布图

对比分析图4和图5，在饱和稳定渗流场的分析中，以浸润线为分界线分割饱和区，若仅认为浸润线以下的饱和区发生渗流，忽略浸润线以上的饱和区域，忽略对部分压力总水头和孔隙水压力的计算分析，这样的分析是不合理的。对比分析了非饱和区在渗流场中的作用，浸润线是饱和-非饱和渗流区的分界线。其下孔隙水压力、总水头值均是正值，反之均为负值。

通过对比分析饱和-非饱和稳定渗流场的分析得出压力总水头、孔隙水压的等值线分布规律大致相同，在实际工程中对二者的分析研究必须结合起来。为了使更加显著区别，对非稳定渗流的课题研究尤为重要。

3 结 论

文章主要是在土石坝饱和-非饱和土体的理论研究基础上，根据有限单元法的基本原理和数学模型的建立，运用有限元程序模拟了正常工况下，饱和-非饱和稳定渗流的浸润线变化趋势，对渗流场中压力总水头、孔隙水压力进行了计算分析，结合工程实际认为计算结果正确合宜，通过等值线分布图验证了坝坡的安全稳定性。同时认为渗流分析是饱和渗流与非饱和渗流有本质的区别，二者的结合分析会更贴近工程实际。

[1]顾慰慈．渗流计算原理及应用[M]．北京：中国建材工业出版社，2000：26-37.

[2]刘杰．土石坝渗流控制理论基础及工程经验教训[M]．北京：水利水电出版社，2005：4-12.

[3]郑敏生，钱镜林，苏玉杰．考虑非饱和区的土石坝渗流分析[J]．水力发电学报，2010，29(01)：186-191.

[4]毛昶熙．渗流计算分析与控制[M]．北京：中国水利水电出版社，2003：1-63，89-124，306-342.

[5]王华俊．锦屏二级水电站闸基深厚覆盖层渗流分析与控制研究[D]．四川：成都理工大学环境与土木工程学院，2005．

[6]柴军瑞．大坝工程渗流力学[M]．拉萨：西藏人民出版社，2001：6-7.

[7]朱晓源．考虑非饱和土体的土石坝渗流与坝坡稳定分析研究[D]．杭州：浙江大学，2006.

[8]黄俊，苏向明．土坝饱和-非饱和渗流数值分析方法研究[J]．岩土工程学报，1990(05) .

Impact Analysis for Saturation and Un-saturation Stability Seepage Field of Earth and Rock Fill Dam

HAN Xue

(Tonghe County Tax Technology Service Center, Tonghe 150900, China)

Earth-rock dam is a common dam type at the present time, and the construction of seepage protection system takes very important roles for the stability of dam body, several safety accidents in water conservancy projects both at home and abroad will arouse enough attention. To analyze the seepage of earth and rock dam needs to be defined as a community of saturation and un-saturation areas, the past experiences have proved them to be supplemented each other. For both the movement characteristics, un-saturation seepage is more complex and the affecting factors are more than saturation seepage. In this paper, combination with the project on-site, the valuable simulation for limited element is applied to draw the changing law of seepage fields in both saturation and un-saturation seepage, concluding a correct theory about seepage filed, and the results studied will have a certain of reference values in constructing the seepage protection system of earth and rock fill dam.

earth-rock dam;un-saturated soil;stable seepage field

1007-7596(2017)05-0023-04

2017-04-18

韩雪(1968-)，女，黑龙江通河人，工程师。

TV641

B