“探索三角形全等的条件(第一课时)”教学实录与反思
■王 涛
“探索三角形全等的条件(第一课时)”教学实录与反思
■王 涛
一、课堂实录
1.复习定义,温故知新。

图1
师:(投影图1。)我们来回顾一下,什么叫作全等三角形?
生1:两个能完全重合的三角形叫作全等三角形。
师:(将△ABC向右平移与△DEF重合。)就像这样,此时3对边、3对角分别重合。也就是说3对边、3对角分别相等。
师:(依次标注3对边和3对角分别相等,如图2。)因此当两个三角形3对边、3对角分别相等,这两个三角形必然全等。

图2
2.创设情境,引出课题。
师:如果△ABC与△DEF是某建筑物上的两块全等的玻璃,但不小心损坏了一块。(投影△DEF破碎的动画,如图3。)请你打电话向安装玻璃的师傅描述一下△ABC,你会说什么?

图3
5位学生依次表达了自己的想法。
师:他们说的究竟对不对呢?这就是我们这节课要探讨的课题,探索三角形全等的条件。(板书课题。)我们知道“3对边、3对角分别相等”可以作为判定三角形全等的依据,但是用这6个条件来判定三角形全等是不是有点麻烦?
生众:是。
师:我们来探讨,减少边或角的条件,它们是否依然全等?现在有两种思路可以选,一种是在6个条件的基础上逐步减少条件来探索。另一种思路是从简单到复杂,从一个条件相等开始探讨。大家想选哪一种?
生众:从简单到复杂。
师:那我们就从简单到复杂来探索,这是认识问题常用的一种方法。
3.体验分类,逐一探索。
师:我们先从一个条件开始探索,这一个条件可能是给定……(欲言又止)
生众:给定一边、一角。
师:你只告诉安装师傅三角形的一条边长,他能切出与△ABC全等的玻璃吗?
生7:不一定。因为只给定一边,所作的三角形的其余两条边长可以不相等。也就是说所作的三角形不一定重合,所以师傅不一定能切出与△ABC全等的玻璃。
师:很好,那给定一角,所作的三角形一定全等吗?
生8:不一定,因为只给定一角,所作的三角形的其余两个内角可以不相等,也就是说所作的三角形不一定全等。
师:你说的有道理。综上,给定一个条件作出的三角形不一定全等。我们再增加一个条件,探讨两个条件,这两个条件可以是……(欲言又止)
生众:给定两边、两角、一边一角。
师:我们来依次探索,给定两边,作出的三角形一定全等吗?
生众:不一定全等。
(实验素材:红色、绿色磁力条若干,且红色磁力条比绿色磁力条短,如图4—图14,用加粗线段代表红、绿磁力条。)

图4
师:(出示红色、绿色磁力条。)给定两边,哪位同学愿意在白板上作出符合条件的三角形?
(生9在白板上作出了符合要求的两个三角形,如图5,图中没有加粗的一边是学生利用三角板连接的线段。)
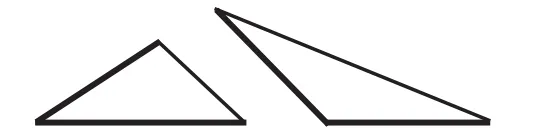
图5
师:你能简单说明一下吗?
生9:可以,我作的两个三角形,虽然有两对边分别相等,但是它们并不全等。这就说明给定两边作出的三角形不一定全等。
师:你讲的很有道理,非常好。那给定两角呢?
生10:即使两个三角形有两对角分别相等,它们也不一定全等,它们可以一大一小。
师:你的意思是,两对角分别相等的两个三角形,虽然形状相同,但是大小可以不一样,是吗?
生10:是的。
师:这就好比我手中的大三角板与你们笔袋中的小三角板,是哪一块小三角板?举起来让我看看。(学生陆续举起。)
师:很好,那给定两角作出的三角形也不一定全等。如果给的是一边一角呢?这个有点难,动手画画看。(教师先在白板上给定一角α,如图6,再巡视学生的画图过程,并邀请一位学生利用红色磁力条在白板上作图,如图7。)

图6

图7
师:你可以简单说明下吗?
生11:我所作的这3个三角形,都符合一边一角分别相等,但它们并不全等。这说明给定一边一角所作的三角形不一定全等。
师:你表达得非常清晰,真棒!(教师看着图7,若有所思。)我想问一下,是不是给定的一边一定得是角α的夹边?
生12:不一定,也可以是角α的对边。
师:你来试试看。(生12在白板上作图,如图8。)符合要求的三角形一定全等吗?
生12:不一定。(他在图8的基础上作了图9。)

图8

图9
师:你真的很聪明,同学们掌声鼓励一下。这说明给定一边一角作出的三角形也不一定全等。综上,给定两个条件作出的三角形不一定全等。继续探索,给定三个条件呢?你能说出有哪几种可能的情况吗?
生13:给定三条边、给定三个角、给定两边一角、给定两角一边。
师:你说的顺序和我想的一致,我们真是心有灵犀。大家觉得哪种情况更容易判断?说说看。
生14:给定三个角更容易判断,因为三个角分别相等的两个三角形,形状虽然相同,但大小可以不一样。
师:你说得真好。因为时间限制,我们只能再探索一种情况,研究哪一种好呢?
生众:给定两边一角。
师:好,那其他情况留给同学们课后加以研究。两边一角,比如这个三角形(如图10),你选哪两边哪一角呢?
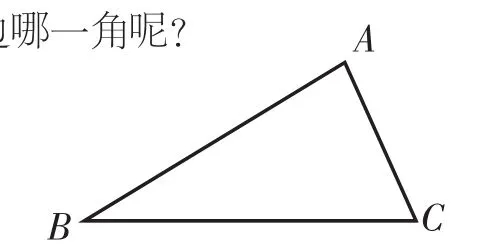
图10
6位学生分别进行了不同选择。
师:你们说的可以归纳为两类,一类是两边和它的夹角,另一类是两边和它一边的对角。我们先来探索给定两边和它一边的对角作出的三角形是否全等,动手画画看。(教师先在白板上给定两边m、n与角α,如图11,再巡视学生的画图过程,并邀请一位学生利用红、绿色磁力条在白板上作图,他作图如图12。)

图11

图12
师问生21:好了吗?
生21:(有点迟疑)我觉得还能作出一种与它不全等的三角形,但不知如何下手。
师:你将红、绿色磁力条换下位置试试看(如图13)。
生21:(又在图13的基础上,作出图14。)我想到了,只要将红色磁力条逆时针旋转,就找到了另一个符合条件的三角形。
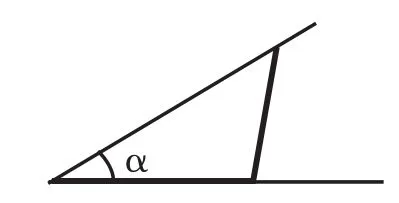
图13
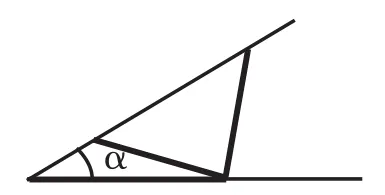
图14
师:你真是个爱动脑的孩子,通过这个操作你得到了什么?
生21:给定两边和它一边的对角作出的三角形不一定全等。
师:是的,那我们再来探索给定两边和它的夹角,按要求在透明纸上作△ABC。如图15,用直尺和圆规作△ABC,使∠B=∠α,AB=m,BC=n.
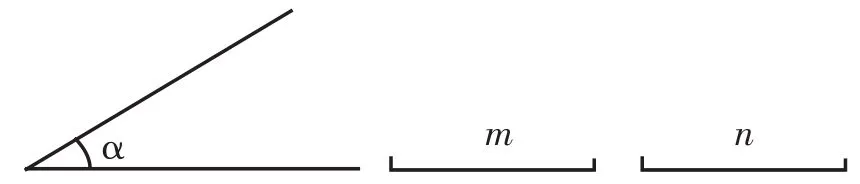
图15
师:(巡视学生的画图过程并指导。)作好之后,组内对比。每组选出代表,组间对比,你们发现了什么?
生众:完全重合。
师:(操作几何画板。)请看大屏幕,改变三角形的边或角,按两边夹一角分别相等所作的三角形依然与已知三角形全等。
(课前教师在画板工具中作好△ABC,并显示AB、BC的长度与∠B的角度。拖动点A、C,改变△ABC的边或角,AB、BC的长度与∠B的角度也随之改变;停止拖动,利用画板工具作DE= AB、∠E=∠B、EF=BC,连接DF获得△DEF,平移△DEF,使之与△ABC重合。)
师:这说明了什么?
生22:两边及其夹角分别相等的两个三角形全等。
4.讲解新知,语言互译。
(学生口述,教师板书上述结论。)
师:这是人们长期实践获得的用来判定两个三角形全等的一个基本事实。可以简写成“边角边”或“SAS”。(教师板书。)几何中的每一个知识点都对应三种语言,文字语言、图形语言、符号语言。通常我们先将抽象的文字语言译成更加直观的图形语言,如图16,△ABC与△DEF的两边及其夹角分别相等,你选哪两边及其夹角分别相等?

图16
3位学生分别进行了不同选择。
师:你们选的都可以,你(学生23)是第一个回答的,我选你说的来标注(如图17)。现在我们再将图形语言译成简洁明了的符号语言,哪位同学试试看?
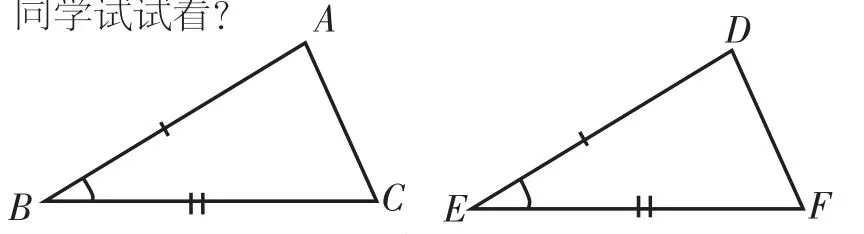
图17
(生26口述,教师板书,过程略。)
师:符号语言你用得很规范,平时解几何题时,我们经常会将这三种语言进行互译,如果你能将它们紧密结合,你会发现几何中定理与性质其实很简单。友情提醒一下,在写判定的条件时,我们要注意顺序,按照“边角边”的顺序来写,而且第一个三角形中的边与角通常要写在左边。
5.拓展应用,生活数学。
题目如下,讲解略。
(1)找出图18中的全等三角形,并说明理由。

图18
(2)已知,如图19,AB=AD,∠BAC=∠DAC。先求证△ABC≌△ADC。再想想,BC=DC吗?CA平分∠DCB
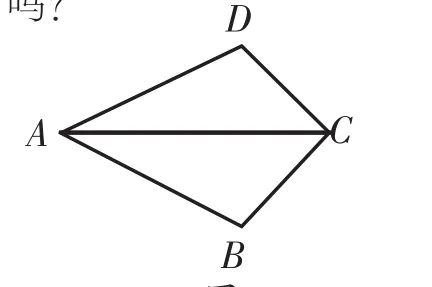
图19
(3)为了测量开山修隧道的长度,测量员的设计如图20所示,O为AD的中点,B、C、O在同一条直线上,且OC=OB,已知CE=30m,DF=60m,只要测出AB的长,就可得隧道EF的长,为什么?当AB=250m时,求隧道EF的长。
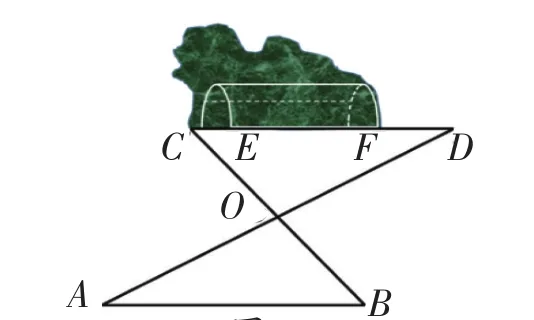
图20
6.课堂小结,分享收获。
师:还记得这节课探索了什么吗?(投影图21。)哪些不一定成立?一定成立的是什么?哪些还没有探索?这就留给你课后去探讨了。

图21
二、教后反思
本课设计遵循的理念就是努力把学习的主动权交给学生,尊重学生、信任学生。教师需要做好的是帮助学生在学习的每一个阶段和每一个具体活动中都表现出明确的目的性,并且始终围绕学习目的开展学习活动,从而保证学习的方向性和有效性。
透明纸、彩色磁力条、几何画板软件的使用不仅省时,更为重要的是为学生提供了直观体验,有助于理解、记忆抽象的数学结论并发展抽象思维。数学教学是数学思维活动的教学,教学中对文字语言、图形语言和符号语言进行了转换,即“换一种说法”,可以更好地启迪学生思维,提高学生数学思维的深刻性和灵活性。
本课遗憾的是,如果时间充足,就可以将三角形全等的条件全部探索出来,这样学生的知识结构就更加完整。如果彩色磁力条有缩小版的,每人一份,那么探索活动将更加有效。
(作者为江苏省连云港市新海实验中学苍梧校区教师)

