EKF在非机动单站无源探测中的应用研究
作者/谢磊、刘宇畅、聂杨,中国电子科技集团公司第二十九研究所
EKF在非机动单站无源探测中的应用研究
作者/谢磊、刘宇畅、聂杨,中国电子科技集团公司第二十九研究所
非机动单站纯方位无源定位系统能估计出远处作匀速直线或分段匀速直线运动的辐射源的运动方向、与观测站的粗略距离等。利用非机动单站无源系统捕获的这些信息,可以在保持“电磁隐蔽”的前提下,进行军事行动及装备部署,因此有着重要的军事应用价值。本文研究了扩展卡尔曼滤波(EKF)在非机动单站无源探测系统中的应用。
非机动单站无源定位;纯方位定位;卡尔曼滤波
引言
ESM作为电子战的一部分,是利用敌方电磁辐射而采取的军事支援行动,包括对电磁辐射信号的搜索、截获、识别、定位等,从而为其它军事行动提供依据[1]。其中,对目标的无源定位有重要意义。
常见的无源定位分为机动平台对静止目标(慢速移动目标)的定位和非机动平台对移动目标的定位。关于前者的相关研究比较多,而后者其实也有着重要研究价值,非机动地面观测站有“电磁隐蔽”和“长时间值守”等优点,特别适合布置于沿海一带,侦察相关空域。本文分析了非机动单站纯方位无源定位系统,对比了最小二乘法和卡尔曼滤波在该系统估计中的应用。
1. 最小二乘法原理
当辐射源距离观测站很远时,可近似认为辐射源做匀速直线运动或分段直线运动(速率恒定,运动方向恒定)。如图1所示,设观测站(静止)位于坐标原点,辐射源由远及近,做匀速直线运运动。系统观测量为ϕk、θk(k=0,1,……,对应不同的时刻)。设观测站与辐射源的距离为rk(k=0,1,……),则辐射源的位置Tk( rk,θk,ϕk),k=0,1,……。设辐射源的速率是v,速度方向为(α,β),其中α是速度矢量在xoy面的投影与y正向的夹角,β是速度矢量与z正向的夹角。
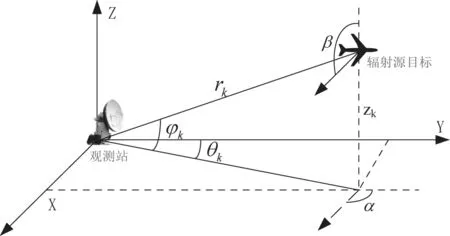
图1 非机动单站纯方位无源定位系统的示意图
辐射源在任意k时刻的状态可用球坐标系来确定(rk,θk,ϕk,v,α, β),其中ϕk、θk为系统观测量。在直角坐标系中,辐射源在时刻k的位置可表示为(xk,yk,zk),速度矢量为(vx, vy, vz),可得:
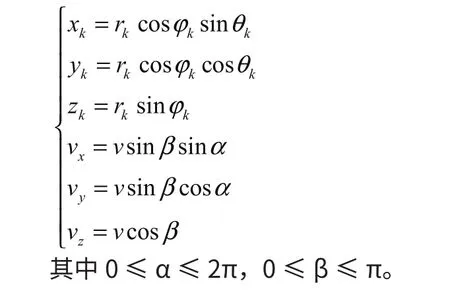
用(xk,yk,zk, vx, vy, vz)也可表示辐射源的状态。在直角坐标系中可利用球坐标中的角度分量ϕk、θk和距离分量rk,于是k时刻辐射源的位置表示为:
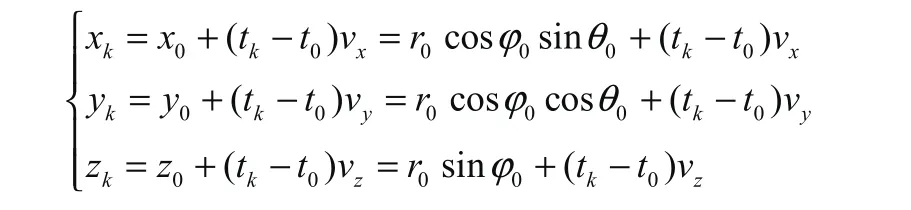
系统方程可表示为:

其中,Wk—1是状态噪声,V1k、V2k是观测噪声
观测量ϕk、θk满足下列方程:

根据上式,用最小二乘法[2]估计出vx/r0、vy/r0、vz/r0。
利用上述方程组的第1个公式,可得:

利用前k个时间内的历史数据进行计算,得到:
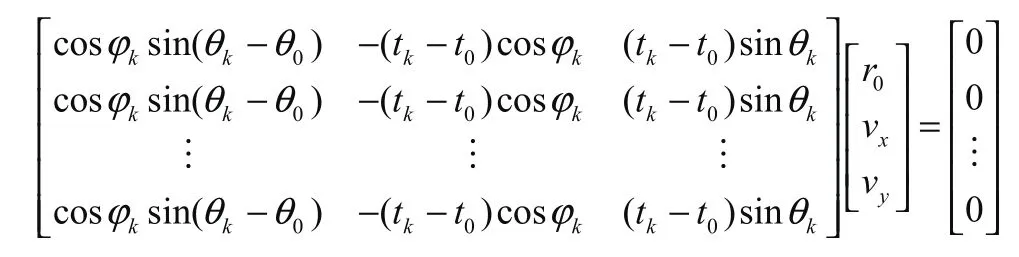
设系数矩阵第1列为A1,第2、3列为A2,则有:
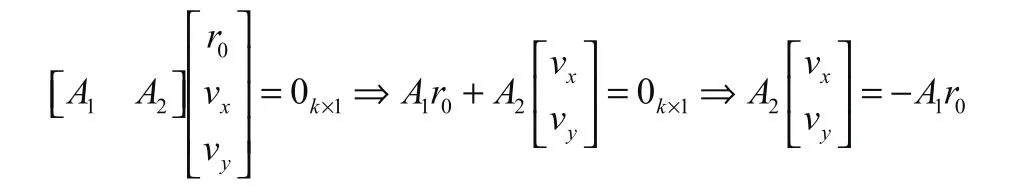
令z0=[vx/r0vy/r0]T,则上式可转换为A2Z0= —A1;
根据文献[15]所提出的方法,用最小二乘法求解,得:
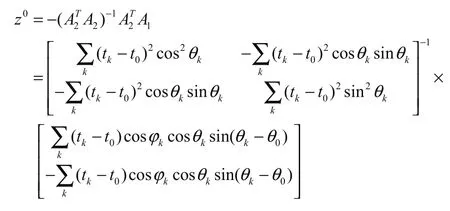
2. EKF算法原理
采用扩展卡尔曼滤波对vx/r0、vy/r0、vz/r0进行估计,Z0=[ vx/r0、vy/r0、vz/r0]T。系统方程表示:

系统的观测方程非线性[3],可使用EKF方法进行估计,假设系统噪声满足下列条件:

EKF算法[4][5]如下,设初值(状态向量的估计值) ; P0|0(估计的均方误差阵),满足:

此时,使用EKF同时估计出系统的三个状态值vx/r0、vy/r0、vz/r0。
3. 仿真对比
场景:观测站静止,坐标为(0,0,0)(m),辐射源匀速直线运动,初始坐标(1051055×103)(m),速度矢量为(300—300 0)(m/s),观察站与辐射源初始距离为2×105(m),速度约424(m/s),方向为(130,90)(度)。假设方位角、俯仰角度观测噪声都服从N(0,0.012)。
(1)利用最小二乘法对辐射源的运动方向(α,β)进行估计,仿真如图2所示。
(2)利用EKF算法对辐射源的运动方向(α,β)进行估计,仿真如图3所示。
对比图2和图3的仿真结果可知:
①在前40次迭代中,最小二乘法总体趋势收敛,但波动较大;而EKF持续收敛,并无波动;
②最小二乘法迭代85次后,角度误差持续小于5度;而EKF迭代50次后,误差就已持续小于5度。
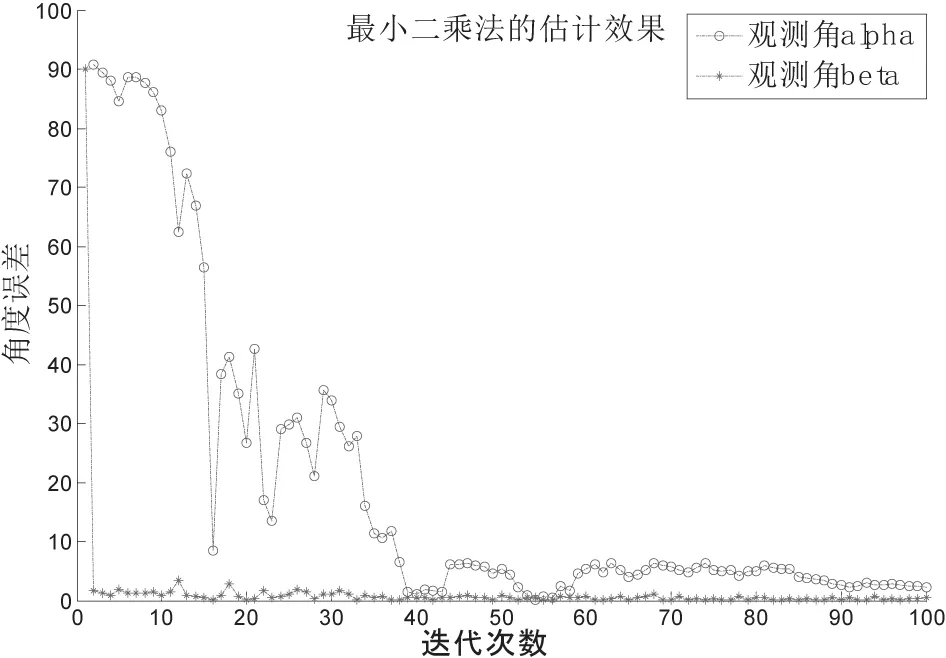
图2 最小二乘算法仿真
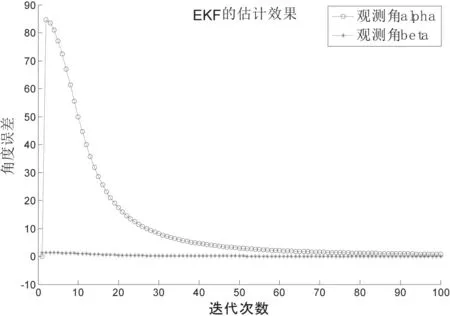
图3 EKF算法仿真
4. 结论
本文对最小二乘法和EKF算法进行了原理介绍,并利用MATLAB对二者进行了建模仿真。最小二乘法需要很多历史数据,对该数据进行“块计算”,而卡尔曼滤波能“忽略历史数据”,做到节省计算量。仿真结果表明,EKF比最小二乘法收敛更快、精度更高。
* [1]赵国庆,雷达对抗原理[M],西安:西安电子科技大学出版社,1999
* [2]董志荣,纯方位系统TMA非线性最小二乘法—理论数学模型与常规算法[J],情报指挥控制系统与仿真技术,第27卷,第1期,2005年2月
* [3]郑大钟,线性系统理论(第2版)[M],清华大学出版社,2002年10月
* [4]袁天鑫,最佳估计原理[M],国防工业出版社,1980年
* [5]詹艳梅,纯方位目标运动分析卡尔曼滤波算法[J],应用声学,22卷,1期

