具有容错性的时间同步协议算法
董仕鹏, 陈 璇
(兰州交通大学 电子与信息工程学院,甘肃 兰州 730070)
具有容错性的时间同步协议算法
董仕鹏, 陈 璇
(兰州交通大学 电子与信息工程学院,甘肃 兰州 730070)
在无线传感器网络的许多时间同步协议中,算法的精确性、高效性以及简洁性总被优先考虑。此外,容错性时间同步协议也逐渐受到越来越多的关注,鉴于经典算法浮动时间同步协议(FTSP)较为全面地考虑了时间同步的能耗、同步精度、可扩展性等要求,提出了一种基于FTSP具有容错性的时间同步协议,算法通过对历史所测的有限个时钟漂移率进行加权平均计算新的漂移率,其中算法的加权系数根据历史测量值的方差动态确定。通过Matalab对新算法的时钟漂移率和在接收到错误信息情况下漂移率的变化进行仿真分析,结果表明:改进后的算法具有较强的容错性。
无线传感器网络; 容错性时间同步协议; 时钟漂移
0 引 言
无线传感器网络(wireless sensor networks,WSNs)融合了无线通信技术、传感器技术以及分布式计算机技术等多种技术,它是由部署在监控区域里大量廉价的、具有存储、感知、通信能力的微型传感器节点组成的自组织网络。WSNs中分布存在的节点能将监控区域内采集到的数据以多跳的方式传递给汇聚节点,汇聚节点转送给中央控制器,从而实现对整个区域的监控。WSNs的应用前景十分广阔,它在军事国防、环境监测、医疗卫生、科学研究等领域均发挥着非常重要的作用[1]。
网络时间同步协议(network time protocal,NTP)是计算机网络上应用最普遍的协议。此外,全球定位系统(global positioning system,GPS)也被用来实现时间同步。由于NTP和GPS功耗较高,成本较大,所以不适合WSNs。比较经典的时间同步算法分别参考广播同步(reference broadcast synchronization,RBS)[2],传感器网络时间同步协议(timing synchronization protocol for sensor networks,TPSN)[3],容错时间同步协议(foult-tolerant time synchronization protocol,FTSP)[4]等。RBS是一种系统的WSNs时间同步算法,同步精度较高,但能耗较大,不适合大型多跳网络。TPSN可实现全网同步,精度高,然而网络扩展性较差。FTSP是目前最为有效的算法,较为全面地兼顾了时间同步的能耗、精度、可扩展性、鲁棒性等要求。
比较几种经典算法发现,算法均较为全面地考虑了同步精度、能耗等问题,但未考虑同步的容错性。由于WSNs分布在比较恶劣的环境中,节点会因为外界因素的干扰或系统软硬件的缺陷产生同步数据误差,如果误差未及时修正,将影响整个网络的时间同步精度,导致无法提供可靠的应用[4]。
1 FTSP实现同步的过程
WSNs时间同步即对节点时钟偏移和时钟漂移率的补偿。时钟偏移指两节点在同一时刻的时钟偏差,时钟漂移则是因为各节点的晶振频率不同而引起的时钟振荡频率的偏差[5]。FTSP算法利用线性回归估计时钟漂移率,进而利用时钟漂移估算和调整全局时间。
FTSP会给每个节点分配一个具有标识作用的ID号。算法执行时,根据ID号动态选取出一个节点作为参考节点。参考节点会定期广播其本地时间,收到广播消息的节点记录下广播时间标和接收广播时的本地时间标。因此,当一个节点接收到参考节点的广播消息后会收集到两个时间标,一个本地时间标和一个参考节点广播的时间标。将本地时间和其与广播消息的差值作为一个时间标对,即参考点。当一个节点积累了至少8个参考点后,即可应用线性回归估算时钟漂移率。通过时钟漂移率估算全局时间偏差,从而与参考节点同步。
2 容错性FTSP
由于时间同步对WSNs的各种应用至关重要,因此,在恶劣环境下,如何提高WSNs节点时间同步的精度以及节点受到恶意攻击后,如何保证节点的抗攻击性已成为近些年的研究热点。
文献[6]提出了一种全新的时间同步协议实时流传输协议(real-time streaming protocol,RTSP),采用了新的图形理论方法,能够在消息层面上检测异常数据。这种细粒度的检测能力使RTSP可以较好地抵抗女巫攻击。但协议的可操作性较差,未充分考虑无线传感器的功耗问题。
文献[7]采用动态选举时间基准节点来避免重复发送的策略,算法增强了网络的可扩展性,对于新加入的节点可以迅速收敛,同时利用残差分析进行差错判断。虽然算法整体上提高了时间同步的容错性,但是通信量较大。
文献[8]提出了一种容错协议,采用分布式算法,由攻击检测模块、本地时间校准模块、加权系数生成模块组成,能够有效地消除同步过程中产生的误差,提高了时间同步的精度,保证了多通道通信的稳定性,但协议结构复杂,不容易实现。
本文在经典算法FTSP的基础上,针对算法线性回归易受异常数据和其他环境因素影响的缺陷,提出了一种新的容错算法,对所测的有限个历史时钟漂移率进行加权平均增加时钟漂移率的精确性,其中,加权系数根据历史测量值的方差动态确定。相比文献[9,10],系数确定更加合理科学,避免了因为依靠经验值产生的不确定因素。
3 FTSP的改进
FTSP用线性回归的方法计算时钟漂移率,在一个周期中,当回归表中收集到8个参考点后,便可计算漂移率[11]
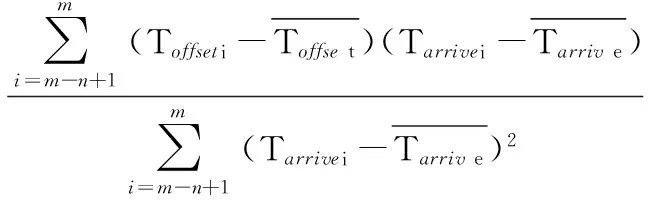
n=8,m≥8
(1)


(2)
式中vi为加权因子

(3)
可以得出,同步周期中测量值的方差越大,其加权系数越小,进而在求解漂移率时比重越小。将式(2)中x和xi用skew′和skewi代替,可得
(4)
结合式(3)、式(4),计算出加权修正后的时钟漂移率
(5)
式中除过方差σ外,其他均为已知量。对于σ计算,从文献[12]可以推断出,在一定时间范围内,节点间的时钟偏差和本地时间具有线性关系
Toffseti=Toffset0+skew×ti+εi,i=1,2,…,N
(6)
式中Toffset0为初始时间节点的时间偏差;ε为随机误差,服从均值为0,方差为σ′2的正态分布。即
εi~N(Toffset0+skewi×ti,σ′2)
(7)
根据式(7),则第m个周期时钟漂移率的方差为

(8)
求出σ后,根据式(5)计算出加权后的时钟漂移率。经过加权后的时钟漂移率稳定性更好,很好地补偿了FTSP算法线性回归易受异常数据影响而不稳定的缺陷。
4 仿真分析
使用Matlab进行仿真分析,仿真参数为:同步周期30 s;回归表中存放参考点个数为n=8;存放历史时钟漂移率个数N=5。在相同条件下,改进的FTSP算法同原FTSP算法进行比较,主要从同步误差以及时钟漂移率2个参数的仿真分布变化情况来分析改进算法的效果。
由图1可知,原FTSP算法平均同步误差大约为1.48 μs,改进的FTSP算法同步误差大约为0.98 μs,相比原FTSP算法,改进的FTSP算法同步误差较小。图2为2种算法时钟漂移率的变化情况,由仿真图可知:原FTSP算法时钟漂移率的波动较大,改进后的算法相对比较平稳。

图1 2种算法的平均同步误差

图2 2种算法的时钟漂移率
为了验证容错性,在同步周期的第10次和第20次时,构建一定的偏差信息。具体方法为使节点接收到的时间信息发生一定的偏差,然后分析仿真。
由图3可知,当接收到含有偏差的错误信息后,在第10次和第20次原FTSP算法的平均同步误差产生了一定的偏差。最大偏差增加到2.9 μs。相比之下,改进的FTSP算法几乎未受到影响。对于图4的时钟漂移率,原FTSP算法在接收到错误信息后,时钟漂移率会产生较大的波动,由于改进的算法应用加权平均,时钟漂移率相对比较稳定。由此证明,改进的算法具有较强的容错性。
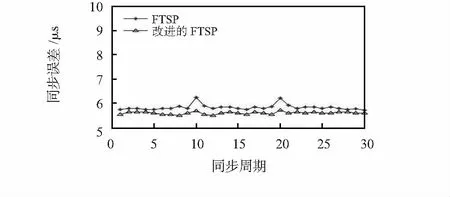
图3 2种算法接收到错误信息的平均同步误差
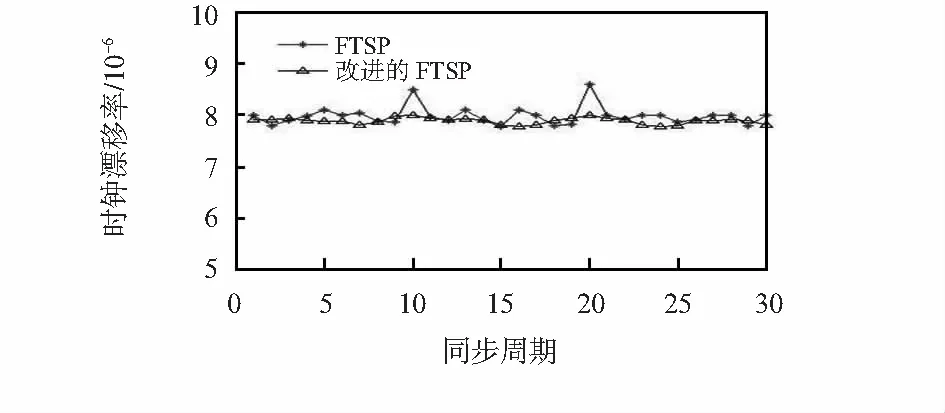
图4 2种算法接收到错误信息的时钟漂移率
5 结 论
对FTSP进行了改进,应用随机加权平均算法对节点的历史漂移率的值进行加权平均,加权平均值增强了FTSP线性回归求解漂移率的容错性。仿真结果表明:改进后的算法不管是从漂移率的稳定程度上还是系统的平均误差方面均有较明显改进。
[1] Mitehel W M,Petter F. Ten emerging technologies that will change the world[J].Technology Review,2003,106(1):33-49.
[2] Elson J E,Estrin D,Girod L.Fine-grained network time synchronization using reference broadcasts[C]∥The Fifth Sympositum on Operating Systems Design and Implementation,2002:147-163.
[3] Ganeriwal S,Kumar R,Srivastava M B.Time-sync protocol for sensor networked[C]∥Proc of 1st International Conference on Embedded Networked Sensor Systems,2003:138-149.
[4] Kusy B,Ledeczi A,Maroti M,et al.The flooding time synchronization protocol[C]∥Proc of 2nd International Conference on Embedded Networked Sensor System,2004:39-49.
[5] 姜 帆,郑 霖.无线传感器网络TPSN-RBS联合时间同步算法[J].传感器与微系统,2016,35(1):149-152.
[6] Dong Wei,Liu Xiaojin.Robust and secure time synchronization aginst sybil attacks for sensor for sensor networks[J].IEEE Journals & Magazines,2015,11(6):1482-1491.
[7] 崔丽珍,园曼曼,李 璋.矿井下WSNs容错性时间同步算法的研究[J].解放军理工大学学报,2015,16(5):418-425.
[8] 秦绍华,陈冬岩.具有容错性的无线传感器网络时间同步协议[J].软件学报,2012,23(1):126-133.
[9] 李秋灵,白 焰,王仁书.具有容错性的泛洪时间同步算法研究[J].计算机仿真,2013,30(12):257-260.
[10] 杨 朔,李长庚.无线传感器网络泛洪时间同步协议安全算法[J].传感器与微系统,2014,33(1):137-140.
[11] 陈 莹,唐加山.无线传感器网络中一种基于FTSP的时间同步协议的改进设计[J].内蒙古大学学报,2012,43(4):409-413.
[12] 何晓群,刘文卿.应用回归分析[M].北京:中国人民大学出版社,2011:18-54.
Algorithm of fault-tolerant time synchronization protocol
DONG Shi-peng, CHEN Xuan
(College of Electronic and Information Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China )
In many time synchronization protocols of wireless sensor networks(WSNs),accuracy,high efficiency and simplicity of the algorithm always be given priority.Besides,fault-tolerant time synchronization algorithm is also paid more attention.In view of classical algorithm floating time synchronization protocol(FTSP),it comprehensively considerates the energy consumption,synchronization precision,scalability and and other aspects that may be requested.propose a fault-tolerant time synchronization algorithm that based on FTSP,the algorithm calculate new clock drift rate through measured historical finite clock drift rate weighted average.The weighting coefficienty is dynamically determined according to variance of historical measurements value.Finally,simulation analysis is carried out on clock drift rate of new algorithm and change of error message
clock drift rate by Matalab.The results show that the improved algorithm has strong fault tolerance.
wireless sensor networks(WSNs); fault-tolerant time synchronization protocol(FTSP); clock drift
10.13873/J.1000—9787(2017)08—0149—03
2016—08—29
TP 393
A
1000—9787(2017)08—0149—03
董仕鹏(1989-),男,硕士研究生,研究方向为无线传感器网络时间同步,E—mail:595935041@qq.com。

