多基地声纳系统中目标位置与速度联合估计*
陈伟伟, 王 鑫
(江南大学 物联网工程学院,江苏 无锡 214122)
多基地声纳系统中目标位置与速度联合估计*
陈伟伟, 王 鑫
(江南大学 物联网工程学院,江苏 无锡 214122)
在多基地声呐系统中,为了利用时间和与多普勒频率量测同时估计运动目标的位置与速度,设计了一种闭式的估计器。其中,使用误差修正的方法,改善了传统的多步加权最小二乘估计器。该估计器只涉及线性加权最小二乘运算,在量测高斯噪声较小的情况下,均方误差可以达到克拉美罗下界(CRLB)。通过计算机模拟对比了该估计器的均方误差与CRLB,并比较了其与传统多步加权最小二乘估计器的性能,结果表明:估计器的均方误差小于传统多步加权最小二乘估计器。
多基地声纳; 时间和; 多普勒频率; 加权最小二乘; 误差修正
0 引 言
由于收发装置合置,单基地声呐在发现目标的同时,也会暴露自己的位置,隐蔽性比较差。而多基地声呐,由于收发装置分置,系统同时具有主动和被动声呐的工作特点,因而在反隐身、反对抗等方面具有潜在的优越性[1]。
在多基地声纳系统中,获得目标的方位角、距离、多普勒频移等测量结果后,经典的维纳滤波[2]、最小二乘估计[3,4]、二次规划[5]、粒子群优化算法[6]可以用来解决目标位置的非线性估计问题。值得一提的是,文献[7]提出了使用多步加权最小二乘来解决非线性定位问题的方法。对于许多非线性估计问题,该方法可以提供一个简单的、闭式的有效估计[8]。
在多基地系统中,基于多步加权最小二乘方法,文献[9]与文献[10]分别研究了只有一个辐射源与有多个辐射源时的平稳目标的位置估计问题。在非多基地的系统中,文献[11]与文献[12]引入了到达信号频差量测,利用多步加权最小二乘方法同时估计运动目标的位置与速度。
当多基地声呐系统中存在一个或多个辐射源,且有时间和与多普勒频率量测时,如何利用多步加权最小二乘方法实现运动目标的位置与速度的联合估计,是本文研究的主要问题。
1 多基地定位问题描述
假设发射站发出的信号传播速度c和载频fc均已知,用τi,j表示ti与sj之间的时间和量测,用fi,j表示ti与sj之间的多普勒频移。由物理分析可得

(1)
(2)
在不影响结论的前提下,为了表述简明,将发射站信号载频fc设定为1 Hz。此时,式(2)可以简化为
(3)
在实际测量过程中,获得的观测量包含噪声,将观测量表示成含噪声的向量形式为
(4)
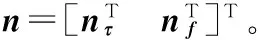
从定位场景出发可推导出CRLB,作为解决该定位问题的估计器所能达到的理论最优性能[10]。观测量m的概率密度函数为

(5)
式中K为归一化常数。
可得该估计问题的CRLB为
(6)
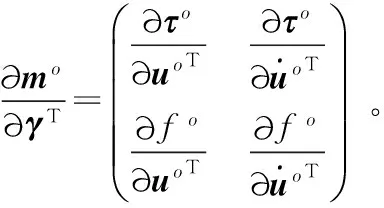
2 位置与速度联合估计器的设计
假定时间和观测量与多普勒频率观测量噪声满足以下条件
(7)
此外,由于二阶及二阶以上的误差项都比较小,在估计处理中忽略这些误差项的影响。
1)将式(1)等号两边同时乘以信号速度c,再将等号右边的‖uo-ti‖-‖ti-sj‖项移到等号左边,等号两边同时平方且忽略误差二阶项的影响,可得
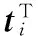
2(ti-sj)Tuo-2(cτi,j+‖ti-sj‖)‖uo-ti‖
(8)
对式(8)求时间的导数,可得
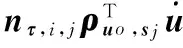
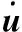
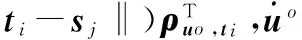
(9)
式中ρuo,ti=(uo-ti)/‖uo-ti‖表示从ti到uo的单位向量;ρuo,sj=(uo-sj)/‖uo-sj‖表示从sj到uo的单位向量。

(10)
式中 矩阵B1,ε1,h1以及G1的具体形式分别为
式中Op×q为p行q列的零矩阵。
式中
式中 0k为k行的零向量。

(11)
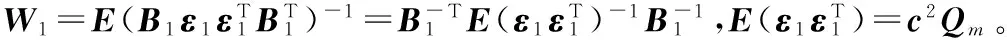
在误差较小的条件下,φ1的协方差矩阵为
(12)
实际计算中,式(11)中的矩阵B1与未知参数γ相关,故首先将矩阵B1中的分块矩阵b11,b21和b22分别设置为单位矩阵,以此来获得γ的初始估计值,然后重新计算获得更加准确的B1。
2)文献[13]在解决两步最小二乘估计器的均方根误差与偏差适应噪声能力差的问题时,提出了误差修正的方法。本文利用该方法改善经典多步加权最小二乘在多基地系统中位置、速度联合估计的性能。
(13)
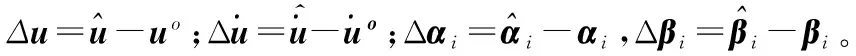
运用Sorenson的方法[14,15],可以得到
(14)
将步骤(1)中待估计量αi的估计值表示为
(15)
对式(15)等号两边同时平方,可以得到
(16)
结合本文的定位场景,根据文献[16]中的定性分析与辅助模拟实验,当目标与发射站之间的距离较大时,估计误差Δαi的二阶项(Δαi)2相对一阶项2αiΔαi很小,可得
(17)
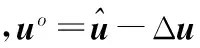
2) ROS与Rovio的通信部分:ROS发出速度指令至Rovio平台,Rovio将当前实际速度值发布到Odom主题,以提供给其他节点订阅。
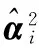
(18)
对βi进行类似αi的处理,可得
αiΔβi+iΔαi≈i-T+Tti+TΔu+(-ti)TΔ
(19)
(20)
式中 矩阵B2,ε2,h2以及G2的具体形式如下
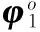
ε2=Δ1
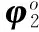
(21)
(22)
式中 W2的具体形式如下
γ=[φ1(1∶2)Tφ1(M+3)∶(M+4))T]T-φ2
(23)
(24)
需要特别指出的是,如果
(25)
那么,结合式(12)与式(22)可得,式(24)的cov(γ)与式(6)的CRLB吻合,即本文提出的估计器是统计有效的。
3 数值模拟实验

3.1 单发射站场景
在单发射站场景中,使用1个信号发射站和5个信号接收站来对运动目标进行定位。发射站坐标为t=[-3 000-4 000]Tm,接收站坐标为s1=[-1 000 3 000]Tm,s2=[2 500-1 000]Tm,s3=[-3 000 1 000]Tm,s4=[2 000 -4 000]Tm,s5=[-2 500 -2 000]Tm。图1(a)给出了单发射站情况下的目标位置和速度估计场景图。
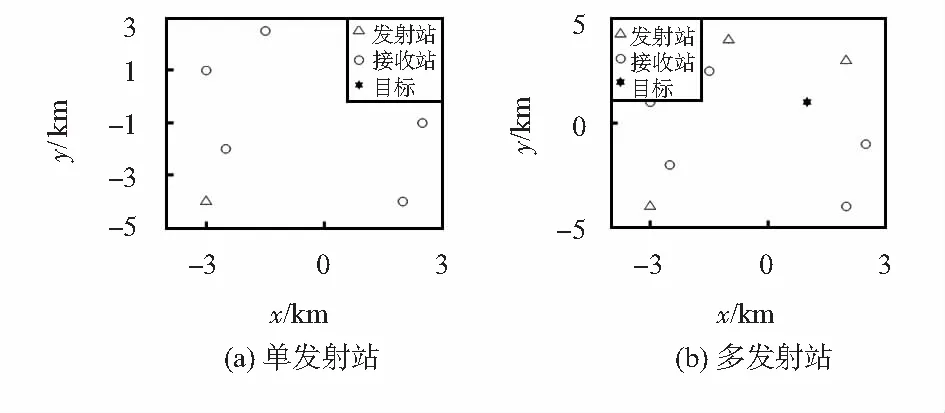
图1 单发射站场景和多发射站场景
图2(a)和(b)分别给出了当στ从0.03逐渐增大到0.3时,本文估计算法、传统多步加权最小二乘法对目标位置和速度估计的均方误差(MSE)的变化曲线。
如图2(a)所示,对于目标位置估计,当στ<0.18时,两种方法的位置估计MSE均能够很好地达到CRLB;当στ>0.18时,本文方法的位置估计精度能够达到CRLB,而传统多步加权最小二乘法的位置估计精度无法达到CRLB,估计性能变差。如图2(b)所示,对于目标速度估计,当στ<0.18时,两种方法的速度估计MSE均能够很好地达到CRLB;当στ>0.18时,本文方法的速度估计精度能够达到CRLB,而传统多步加权最小二乘法的速度估计MSE逐渐偏离目标速度估计的CRLB,估计性能逐渐变差。
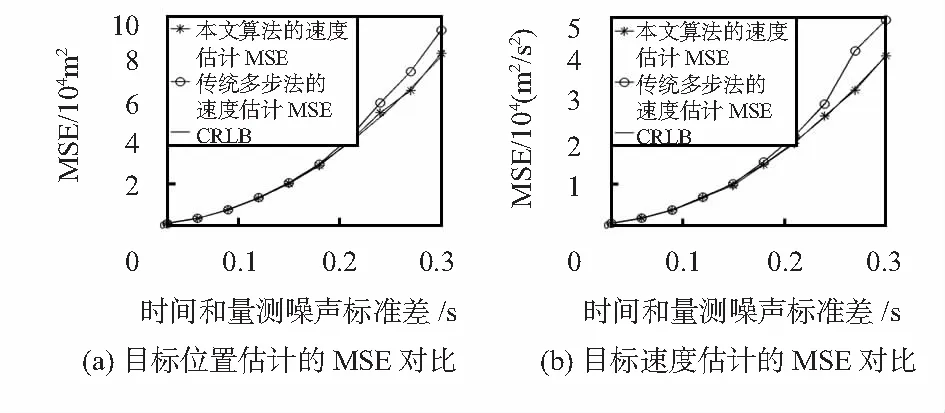
图2 目标位置和速度估计的MSE对比
3.2 多发射站场景
在多发射站场景中,使用3个信号发射站和5个信号接收站来对运动目标进行定位。发射站坐标分别为t1=[2 000 3 000]Tm,t2=[-1 000 4 000]Tm,t3=[-3 000 -4 000]Tm。接收站的坐标设定与单发射站场景相同。图1(b)给出了多发射站情况下的目标位置和速度估计场景图。
图3给出了当στ从0.04逐渐增大到0.6时,本文估计算法、传统多步加权最小二乘法对目标位置和速度估计的均方误差的变化曲线。
如图3(a)所示,对于目标位置估计,当στ<0.36时,两种方法的位置估计MSE均能够很好地达到CRLB;当στ>0.36时,两种方法的位置估计精度逐渐偏离CRLB,而传统多步加权最小二乘法的位置估计精度的偏离幅度明显大于本文算法的位置估计精度的偏离幅度。
如图3(b)所示,对于目标速度估计,当στ<0.44时,两种方法的速度估计MSE均能够很好地达到CRLB;当στ>0.44时,两种方法的位置估计精度逐渐偏离CRLB,本文算法的速度估计精度偏离幅度略小于传统多步加权最小二乘法速度估计的偏离幅度。
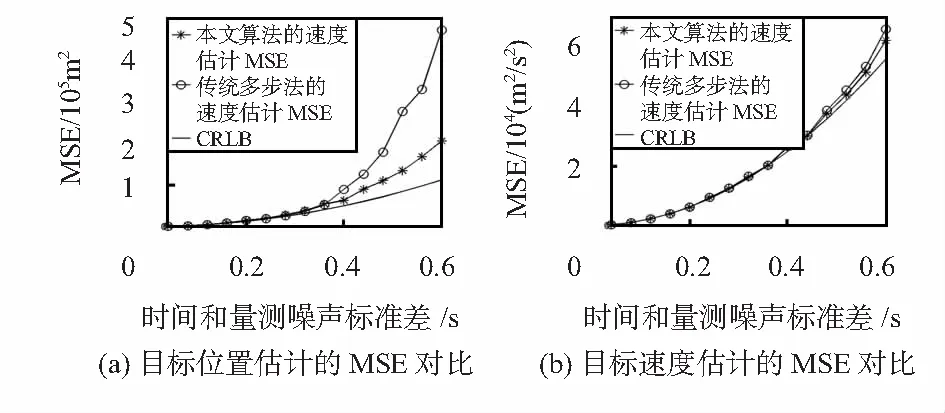
图3 目标位置和速度估计的MEMS对比
仿真结果表明:在单发射站和多发射站两种情况下,本文提出的目标位置和速度的估计算法优于传统多步加权最小二乘法。
4 结 论
为解决多基地声呐系统中运动目标的位置与速度的联合估计问题,在传统多步加权最小二乘估计器的基础上,本文提出了一种新的基于误差修正的估计器。理论分析与仿真实验表明:在量测噪声较小时,该估计器是统计有效的。原理上,本文提出的估计器仅涉及线性加权最小二乘计算,是一个闭式的估计器,不存在局部收敛或者发散的问题。
[1] 肖超超,杨日杰,韩建辉.多基地声纳搜索性能模型研究[J].系统仿真学报,2014,26(6):1315-1319.
[2] Simakov S.Localization in airborne multistatic sonars[J].IEEE Journal of Oceanic Engineering,2008,33(3):278-288.
[3] 叶 永,陈建峰,张 竹,等.基于非线性规划模型的分布式声定位算法研究[J].传感器与微系统,2013,32(2):46-49.
[4] 徐原博,钟丽鸿,崔 洋,等.基于无线传感器网络的极大似然定位法的分析[J].传感器与微系统,2011, 30(10):37-40.
[5] Chan Y T,Ho K C.Simple and efficient estimator for hyperbolic location[J].IEEE Transactions on Signal Processing,1994,42(8):1905-1915.
[6] 翟彦蓉,黄 欢,张 申,等.改进粒子群优化算法在TDOA定位中的应用[J].传感器与微系统,2013,32(4):145-148.
[7] 徐 征,曲长文,骆卉子.无需中间变量的多运动站时差定位新算法[J].航空学报,2014,35(6):1665-1672.
[8] Einemo M,So H C.Weighted least squares algorithm for target localization in distributed MIMO radar[J].Signal Processing,2015,115:144-150.
[9] Rui Liyang,Ho K C.Elliptic localization: Performance study and optimum receiver placement[J].IEEE Transactions on Signal Processing,2014,62(18):4673-4688.
[10] Rui Liyang,Ho K C.Efficient closed-form estimators for multi-static sonar localization[J].IEEE Transactions on Aerospace & Electronic Systems,2015,51(1):600-614.
[11] Yu Huagang,Huang Gaoming,Gao Jun,et al.An efficient constrained weighted least squares algorithm for moving source location using TDOA and FDOA measurements[J].IEEE Transactions on Wireless Communications,2012,11(1):44-47.
[12] Yu Huagang,Huang Gaoming,Gao Jun.Approximate maximum likelihood algorithm for moving source localization using TDOA and FDOA measurements[J].Chinese Journal of Aeronautics,2012,25(4):593-597.
[13] 刘 洋,杨 乐,郭福成,等.基于定位误差修正的运动目标TDOA/FDOA无源定位方法[J]. 航空学报,2015, 36(5):1617-1626.
[14] Huang Jun,Xue Yanbo,Yang Le.An efficient closed-form solution for joint synchronization and localization using TOA[J].Future Generation Computer Systems,2013,29:776-781.
[15] Wang Yinggui,Huang Jun,Yang Le,et al.TOA-based joint synchronization and source localization with random errors in sensor positions and sensor clock biases[J].Ad Hoc Networks,2015,27:99-111.
[16] Xu B,Qi W D,Wei L,et al.Turbo-TSWLS:Enhanced two-step weighted least squares estimator for TDOA-based localization[J].Electronics Letters,2012,48(25):1597-1598.
Joint estimation of position and velocity of target in multistatic sonar system*
CHEN Wei-wei, WANG Xin
(School of Internet of Things Engineering,Jiangnan University,Wuxi 214122,China)
A closed-form estimator is designed to estimate the positon and velocity of the target jointly with time sum and Doppler frequency measurements in multistatic sonar system.The esimator improves traditional multi-stage weighted least squares(WLS)estimator with error correction technique.The estimator involves linear WLS computation only and its mean square errors(MSE)can attain Cramer-Rao lower bound(CRLB)when the measurement Gaussian noise is small.Simulations are conducted to compare the MSE of the proposed estimator with the CRLB and compare its performance with that of the traditional multi-stage WLS estimator.The MSE of the proposed estimator is lower than that of the traditional multi-stage WLS estimator.
multistatic sonar; time sum; Doppler frequency; weighted least squares(WLS); error correction
10.13873/J.1000—9787(2017)08—0106—05
2016—08—03
国家自然科学基金资助项目(61304264);江苏省自然科学基金资助项目(BK20140166)
TN 911.23; TN 953
A
1000—9787(2017)08—0106—05
陈伟伟(1990-),男,硕士研究生,主要研究方向为多基地运动目标定位算法。
王 鑫(1981-),男,通讯作者,博士,讲师,主要研究方向为传感器网络与多源信息融合,E—mail:wangxin@jiangnan.edu.cn。

