珠江口盆地B油田储量参数概率分布

涂 乙，杨 娇，王秀玲，万 钧

(中海石油(中国)有限公司 深圳分公司，广东 深圳 518000)



珠江口盆地B油田储量参数概率分布

涂 乙，杨 娇，王秀玲，万 钧

(中海石油(中国)有限公司 深圳分公司，广东 深圳 518000)

针对珠江口盆地某油田圈闭面积大、构造不规则且井资料少等问题，为了准确获取储量大小、潜力和风险，采用概率法进行储量快速评估是目前最为有效的方法。以B油田Z5油藏为例，考虑到该油藏构造两翼较陡以及中间过渡带较长且井控程度较低，采用面积-厚度-形状因子法构建岩石体积模型，提出根据油藏形状分为N个模块，分模块精细刻画Z5油藏形态，降低构造形态不规则对储量的影响。其中有效厚度、孔隙度采用对数正态分布，含油饱和度采用正态分布，含油面积、体积系数和原油密度均采用单值分布模型，建立各参数概率分布以及储量概率分布模型。结果表明，概算法Pmean储量结果与该油藏确定性方法计算储量规模接近，两者误差不到4%。结合地质参数对储量大小敏感性分析结果，可指导油藏部门进行储量敏感性、经济性、风险和潜力的深入研究，为开发方案与决策的制定提供依据。

概率法；储量参数；储量计算；珠江口盆地

海上油田的勘探开发具有高风险、高投入、高科技等特点，往往在油田开发前期，面临钻井数量少、探井分析化验资料不足以及测试资料有限等问题，导致储量参数选取存在较大不确定性，地质认识程度不高，所计算得到的地质储量风险较大。目前常用的储量评估方法包括类比法、动态法和容积法[1-5]。其中，类比法只应用在钻探前对圈闭远景储量的估算，该储量达不到国家储量委员会审核标准要求；动态法要求油气田开采一定时间，然后根据压降、采油曲线等进行储量估算；容积法是目前应用最为广泛的方法，适用于不同的勘探开发阶段、不同圈闭类型和不同的油藏驱动类型，容积法又分为确定法和概率法。20世纪80年代国内引进蒙特卡罗法进行储量评估，对储量计算参数样本进行预处理，将各储量参数视为随机变量，进行各个参数不确定性分析，建立储量参数最优概率密度函数，随后计算得到地质储量的概率分布，以此来分析地质储量潜力和风险[6-7]。如今国内外采用概率法进行储量评价[8-10]，并对储量计算参数概率分布以及不确定分析较多，而很少将油藏形态反映在储量评价过程中。众所周知，不规则形态油藏与规则形态油藏对于地质参数的选取是不一样的，倘若2种不同类型油藏，只钻遇1口井，测井解释井点参数一样，所选的储量参数势必也一样，简单应用概率法进行储量不确定评价，就很难真实地反映地下储量分布规律。

本文以珠江口盆地B油田为例，以测井解释数据为基础，采用概率法进行储量估算，并引入“形状因子”手段，将不规则油藏进行细分模块，精细刻画油藏构造形态，降低构造形态不规则以及井控程度低对地质储量的影响，同时，对影响储量变化的参数进行敏感性分析，储量评价结果考虑因素更为客观、全面，以期为海上油田制定合理、高效开发方案提供技术支持，降低开发投资风险。

1 概率法储量评估

1.1 概率法发展历程

在1997年之前，国际上采用的是确定性法对储量进行评估，然而在1997年，SPE和SEC联合颁布规定承认概率法储量评估结果，概率法开始被国内外很多石油公司所采用。尤其近些年，国内越来越多的陆地和海上油气田采用概率法进行储量评估，使得概率法得到快速发展与应用[10-11]。概率法以概率论为基础，以储量各个参数概率分布视为随机变量，运用容积法公式计算储量，得到一条储量概率分布曲线，即不同地质储量下的概率值，据此进行客观、合理地评价油田储量潜力和风险[12-14]。

1.2 评估方法

概率法和确定法储量评估均采用的是容积法计算公式：

OOIP=100A·H·φ(1-Swi)ρo/Boi

式中：OOIP为原始地质储量，104t；A为含油(气)面积，km2；H为平均有效厚度，m；φ为平均孔隙度，%；Swi为平均原始含水饱和度，%；ρo为地面原油密度，g/cm3；Boi为平均地层原油体积系数。

主要采用了REP软件对地质储量进行了概率分布研究。岩石体积(GRV)模型计算方法包括①单值分布法、②面积—厚度(等值线)法和③面积—厚度—形状因子法，根据不同类型的含油气构造和油藏，应用不同的计算方法。对于简单、规则、小型的构造油藏可以用单值分布法；对于形状不规则的油藏可采用后2种方法；对于井少、井控范围小以及不规则的油藏适用第三种方法，该方法中形状因子的引入，可以降低构造不规则和井控程度低对储量带来的影响。但是目前对于形状因子的研究有限，只是简单地套用一个构造形状因子进行计算，而实际油藏形状不可以是典型的、理想的，需要进行更深入的研究。本文基于此，对影响储量分布的形状因子进行了细致的刻画，将不规则油藏细分为N个小模块，然后计算每一模块的面积和体积，尽量减小与实际油藏形状的偏差。

1.3 评估流程

(1)储量样品数据统计。可借助Petrel或Excel工具对研究区井点数据资料进行统计，包括孔隙度、饱和度、净毛比、泥质含量等参数，排除极大值和极小值等奇异值，筛选真实井点数据，统计油藏含油面积以及岩石体积。

(2)地质参数概率分布模型选取。岩石体积模型选取方法包括单值分布法、面积—厚度(等值线)法和面积—厚度—形状因子法，针对不规则油藏形态选取第三种方法更为合适。储量参数模型选取方法包括Single、Triangular、Uniform、Lognormal和Normal Beta等，并采用A-D、K-S和χ2检验法对储量参数样本数据的有效性进行检验，最终选择储量参数最优概率密度函数。

(3)评价结果输出。通过容积法计算公式，进行2000次以上的随机模拟，得到储量P10、P50、P90和Pmean数值以及储量概率分布曲线，并对影响储量参数进行敏感性分析，最终得到储量评估结果。

2 应用效果分析

根据以上储量概率评价方法和流程，以珠江口盆地B油田Z5油藏为例(Z5油藏只有探明级别储量)，主要来研究建立储量参数概率分布模型流程，以及考虑不规则油藏形态，对比和分析储量概率分布结果。

2.1 油田概况

B油田位于珠江口盆地中央隆起带，构造是发育在基底隆起上的低幅度披覆背斜，构造简单完整，在含油范围内无断层发育；油层分布在珠江组和珠海组地层；含油范围内构造整体平缓，两翼稍陡，两翼构造倾角较大，构造长轴方向为北西—南东向，短轴方向为北东—南西向。目前B油田有3口探井/评价井，该油田DST生产数据结果显示，珠江组、珠海组均获得了工业油流。2012年对三维

地震资料进行了重处理，结合3口实钻井资料，对B油田构造重新进行精细解释。其中B-1井和B-2井处于构造南翼，且相距较近；B-3井处于构造北翼，南北翼相距约1.5 km，油藏圈闭展布形态呈马鞍状，含油构造圈闭南北边界距离约2.2 km(图1)。

2.2 参数概率分布

B油田3口钻井分布在狭长型圈闭两头，两翼构造高点相距1.5 km左右，中间过渡带区域范围较大且井控程度低。本次收集了3口井的地震、测井解释以及岩心等资料，建立了储量参数概率分布模式(表1)[13-15]。表1中各储量参数赋值主要来源于对各储量参数数据统计结果。以有效孔隙度概率分布为例，根据Z5油藏3口井孔隙度资料数据，以测井解释等间距(0.15 m)取样，共计52个，数据分析均值为18.1%。

本次选取Lognormal、Normal和Beta等3种孔隙度分布模型，并采用A-D、K-S和χ2检验法对孔隙度样本数据进行有效性检验[14-15]。检验结果表明，Lognormal分布概率最小，说明Lognormal分布模式能较好地反映孔隙度数据特征(表2)；同时地质含义检验，孔隙度端点P1为22.9%，端点P99为12.7%，均在置信范围内，且P10/P90比值为1.80，不高于10，表明孔隙度数据分布是合理的。根据SPE与SEC相关规定，对孔隙度数据进行检查，测井解释孔隙度均值为18.1%，孔隙度P90为15.9%，孔隙度P10为20.7%，P90与P10数值在均值±15%范围(15.4%～20.8%)内，说明测井解释孔隙度数据分布是合理的[15-17]；孔隙度采取Lognormal概率分布模型(图2a)。

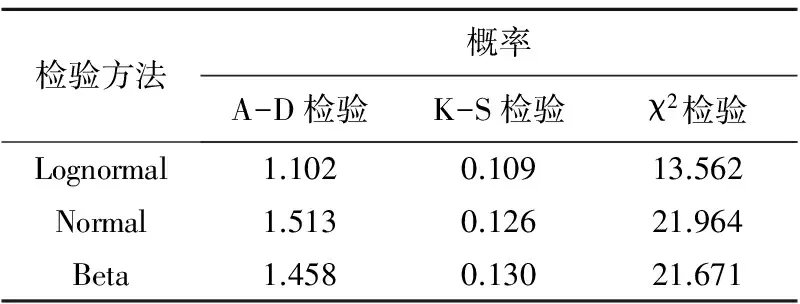
表2 有效孔隙度样本数据数学检验

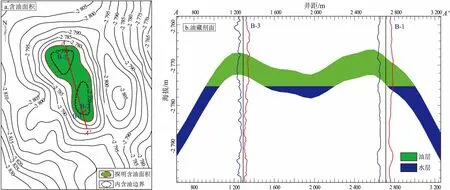
图1 珠江口盆地B油田Z5油藏含油面积与剖面展布Fig.1 Oil-bearing area and reservoir profile of the Z5 reserve, B oil field, Pearl River Mouth Basin表1 珠江口盆地B油田储量参数概率分布模型Table 1 Probability distribution modeling of reserve parameters in B oil field, Pearl River Mouth Basin

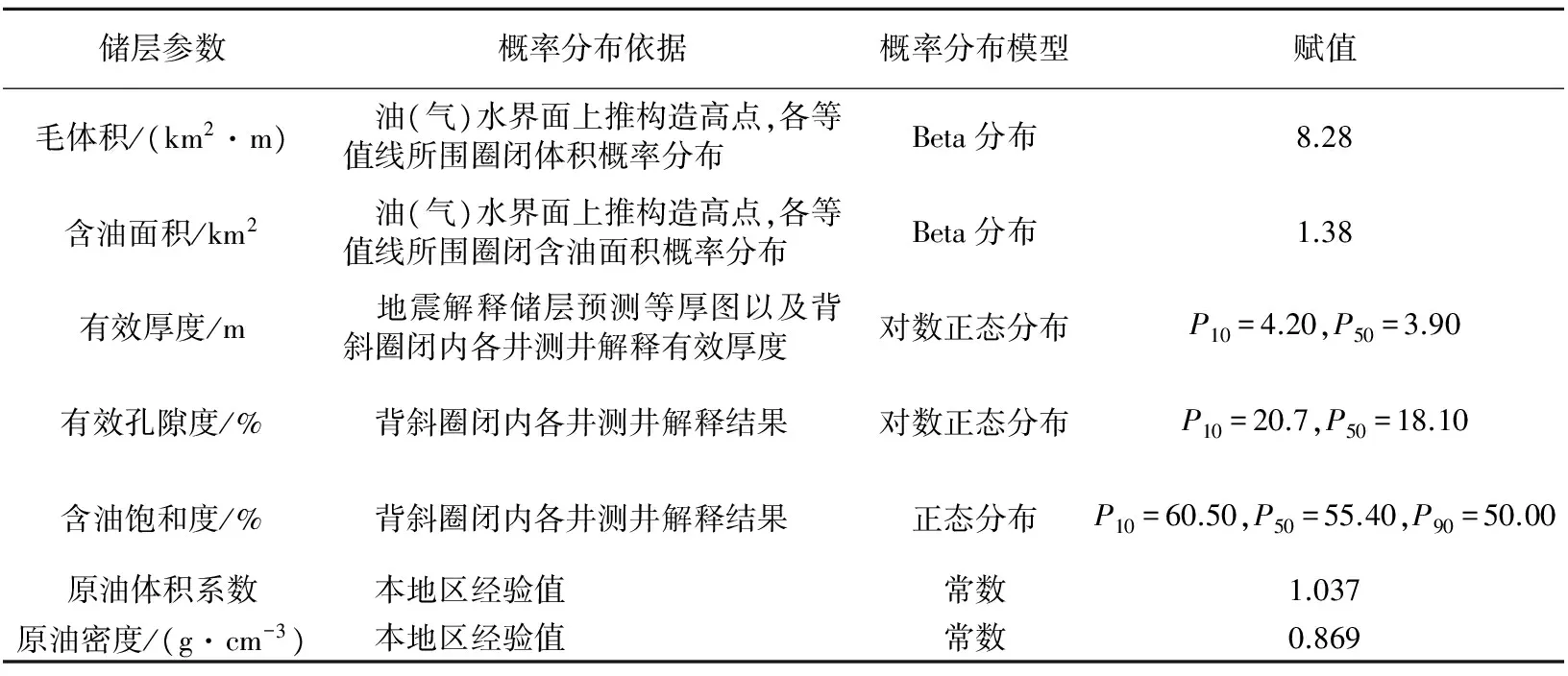
储层参数概率分布依据概率分布模型赋值毛体积/(km2·m) 油(气)水界面上推构造高点，各等值线所围圈闭体积概率分布Beta分布8．28含油面积/km2 油(气)水界面上推构造高点，各等值线所围圈闭含油面积概率分布Beta分布1．38有效厚度/m 地震解释储层预测等厚图以及背斜圈闭内各井测井解释有效厚度对数正态分布P10=4．20，P50=3．90有效孔隙度/% 背斜圈闭内各井测井解释结果对数正态分布P10=20．7，P50=18．10含油饱和度/% 背斜圈闭内各井测井解释结果正态分布P10=60．50，P50=55．40，P90=50．00原油体积系数 本地区经验值常数1．037原油密度/(g·cm-3) 本地区经验值常数0．869

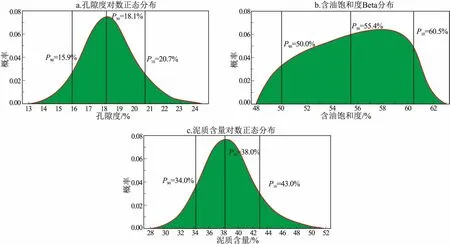
图2 珠江口盆地B油田Z5油藏储层参数概率分布Fig.2 Probability distribution of reserve parameters in the Z5 reserve, B oil field, Pearl River Mouth Basin

根据孔隙度数据检验和选取分布模型原则，分别对含油饱和度、泥质含量和含油面积等参数进行了概率分布分析(图2b-c)，三者均采用单值分布模型，本次不作概率分布[18-19]。Z5油藏毛体积为8.28 km2·m，含油面积均值为1.38 km2，有效孔隙度均值为18.1%，含油饱和度均值为55.4%。

2.3 形状因子确定

引入形状因子可实现对不规则油藏进行精细刻画，形状因子的确定是本次研究的关键，具体确定原则：①通过面积比Ratio确定形状模型。形状模型是指最为贴近真实油藏构造展布的理想形态，面积比Ratio是本次等值线面积与前一个等值线面积之比；②基于上一步确定的形状模型，计算等值线体积来确定形状因子大小。

2.3.1 形状模型判断

(1)A1/A0>0.5时，采用圆柱体形模型，a、b等值线间面积A=[A1+A0+ Sqrt(A1·A0)]/3，a、b等值线间体积V=A·Δh，Δh为等值线之差；(2)A2/A1<0.5时，采用金字塔形模型，b、c等值线间面积A=(A1+A2)/2，b、c等值线间体积V=A·Δh(图3)。

2.3.2 形状因子确定

形状因子=小于等值线体积/(含油面积×厚度)，从油水界面起，往构造高点推，本次计算等值线以下的体积与ΔV=A0·∑Δh。

(1)REP软件在未考虑油藏形态时，体积计算方法ΔV=A0·∑Δh，A0为含油面积，由油水界面向上类推厚度间距Δh，来计算体积。(2)在考虑油藏形态，精细刻画情况下，体积计算方法：第一条等值线以下的体积(油水界面位置)对应的体积为0，往上推第二条等值线以下的体积VA0-A1=V总-VA1-An，第三条等值线以下的体积VA0-A2=V总模型体积-VA2-An，n为等值线条数，其余依次类推，在计算过程中，每一条等值线对应的面积是变化的，充分考虑了油藏形态的变化。

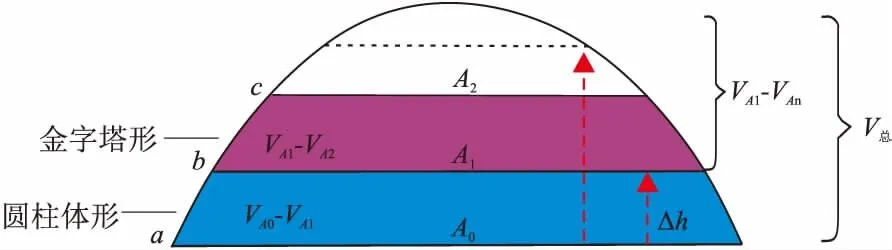
图3 面积比判别形状模型示意Fig.3 A model discriminating shape by area ratio

2.3.3 Z5油藏分块精细刻画

根据油藏储层厚度和形态，纵向上以1 m毛厚间隔，从油水界面往构造高点上推，分为多个模块，通过对邻近两模块的含油面积进行对比，来选取形状模型，确定好形状模型，就可以得到该模块最优含油面积的计算公式，再根据小于等值线体积与含油面积×厚度的比值，得到该模块的形状因子(表3)。

从表3可知，毛厚从1 m到7 m，表示Z5油藏储层越来越远离油水界面，储层厚度变大，油藏构造形状开始以圆柱体形为主；随着油藏厚度逐渐变大，油藏构造形状越接近金字塔形。本次主要选取了面积比方法来对Z5油藏形状模型进行判别，与体积比判别形状模型相比，其计算误差要小，因此，采用面积比对形状模型进行简单的判别。

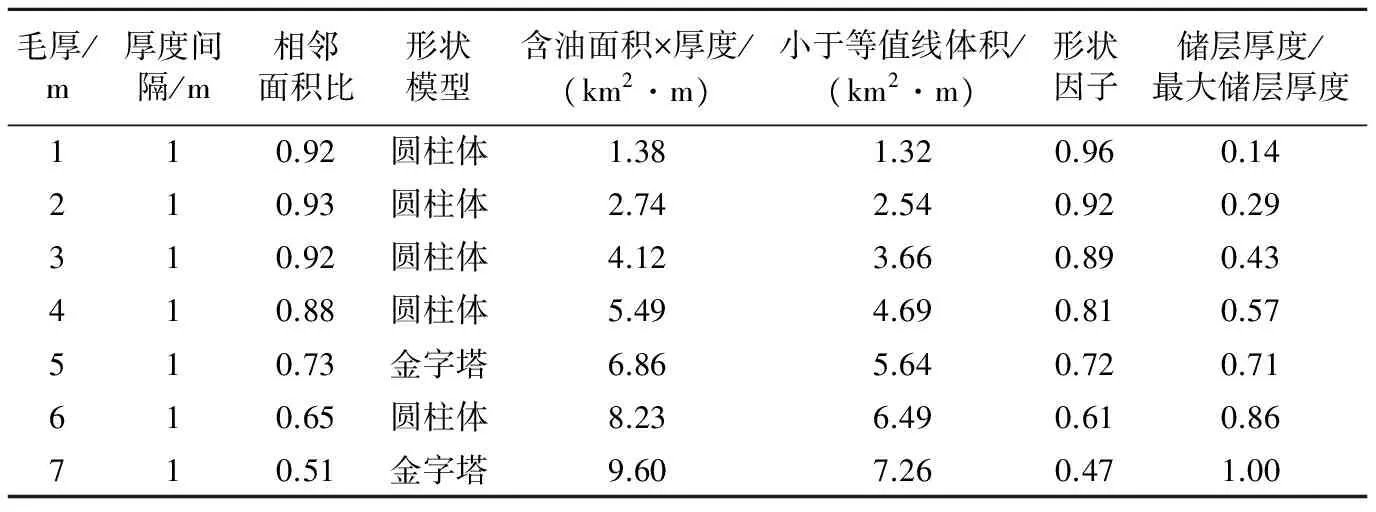
表3 珠江口盆地B油田Z5油藏形状因子统计

从表3可以得到储层厚度和形状因子间具有负相关性，油藏形状与油藏驱动类型、储层厚度/最大储层厚度是相关的，可以统计油藏储层厚度/最大储层厚度和形状因子数据，得到两者的关系式，来确定形状因子的大小分布规律。一般来讲，底水油藏或块状体储层采用角锥体，边水或层状油藏采用等效圆柱体或棱柱体模型。由于B油田Z5油藏展布形态不规则，本次采用面积—厚度—形状因子法进行储量评估更为合理，将形状因子作为储量计算的参数之一，根据形状因子数据分布，选取形状因子Pmax、P10、P50、P90和Pmin进行分析并参与储量计算。

2.4 应用结果分析

基于以上储量参数概率分布结果以及形状因子分布情况，经2 000次蒙特卡洛随机模拟，最终得到B油田Z5油藏储量概率累计分布结果(图4)[20-22]。储量P10/P90检验比值为1.58，在允许的合理范围内[23-26]。根据该油田DST生产数据显示，Z5油藏具有工业油流，具有客观的生产价值，计算得到的较落实的储量与本次概率法计算的储量Pmean误差仅为4%，两者结果基本一致，说明储量概率分布结果符合实际油田情况。

Z5油藏含油构造长轴方向为北西—南东向，短轴方向为北东—南西向，3口井分布两翼，两翼构造较陡，中间是平缓过渡带，这部分平缓带由于井控较小，在不作考虑情况下随机选取模拟方法会影响岩石体积的大小，不能真实地反映地质实际情况。采取面积—厚度—形状因子法，以实钻井点深度数据为辅助，充分考虑构造形状对储量概率分布的影响，按照油藏形态细分N个模块，刻画出储层构造形态，减小了岩石体积计算误差。由图4a和4b可知，采用面积—厚度—形状因子法，最终得到的不同概率下地质储量和可采储量分布规律。由于Z5油藏只有探明级别储量，P50储量应该在该油藏探明储量理想值上下波动，应与Pmean储量基本一致。从图4可知该方法计算得到的Pmean储量与确定法计算结果最为接近。

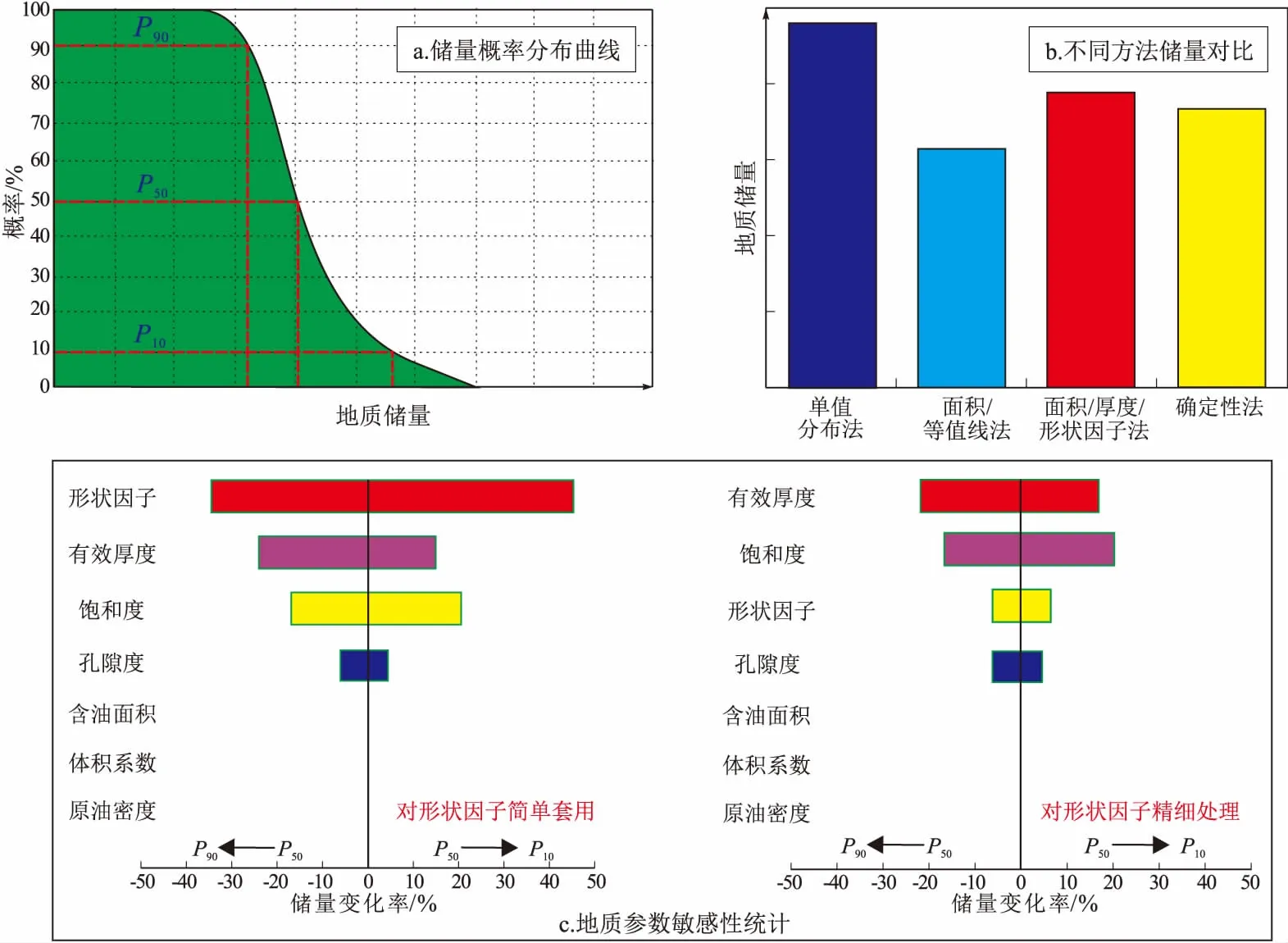
图4 珠江口盆地B油田Z5油藏储量评估结果Fig.4 Reserve evaluation of Z5 reserve, B oil field, Pearl River Mouth Basin

由图4c可知，形状因子简单套用和精细处理后，敏感性地质因素对地质储量以及可采储量影响大小均有所不同。以Z5油藏为例，形状因子使用前，构造形态、有效厚度、饱和度、孔隙度影响储量相对变化率分别约为45%，20%，15%，3%；而对构造形态精细刻画后的形状因子对储量影响降低了，影响储量大小因素排序变为有效厚度>饱和度>形状因子>孔隙度，构造形态影响储量相对变化率下降为5%左右，影响储量相对变化率降低了约40%，说明油藏形态的精细刻画可以大大降低油藏不规则形态对储量大小的影响，但是不能绝对消除构造形态不规则的影响。最终得到的Pmean概算储量与确定性储量结果偏差不到4%，说明储量概率分布规律是符合实际油田情况的。结合地质参数对储量影响敏感性分析结果，可以有效降低Z5油藏储量开发开采风险，提高了对该油藏储量潜力的综合认识，将为油藏做储量敏感性分析、开发方案和决策的制定提供数据支持。目前概率法储量评估已经在海上油田前期目标评价方面进行了广泛的应用，为油田储量潜力和风险快速评价提供了坚实的数据基础。

3 结论

(1)以珠江口盆地B油田3口井测井解释样品数据(等间距0.15 m)为基础数据，采用A-D、K-S和χ2检验法对有效厚度、有效孔隙度以及含油饱和度等地质参数进行分布模型检验，同时以地质含义检验和SPE与SEC相关规定为辅助手段，对样本数据进行有效性检验，数据有效性检验更为全面。

(2)含油面积采用Beta分布模型，有效厚度、有效孔隙度采用对数正态分布，含油饱和度采用正态分布，建立的参数最优概率分布函数，定量化各油藏参数分布，反映油田基本情况更为可靠。

(3)Z5油藏含油构造具有特殊性，两翼较陡，中间平缓带较长，井控不到的部位对岩石体积的计算不够准确。提出利用圆柱体—金字塔形状因子精细刻画油藏构造形态，降低不规则构造形态以及井控程度低区域对地质储量评价误差，使得不规则构造形态影响储量相对变化率由45%下降到5%左右，最终得到的Pmean概算储量与确定性储量结果偏差不到4%，快速获取的储量概率分布结果可靠性较高。结合储量敏感性因素分析成果，可有效降低对地质储量认识风险，指导油藏进行储量敏感性、风险、潜力分析，为开发方案制定提供依据。

[1] 陈元千,周翠.中国《页岩气资源/储量计算与评价技术规范》计算方法存在的问题与建议[J].油气地质与采收率,2015,22(1)：1-4.

Chen Yuanqian,Zhou Cui.Problems and recommendations for the Regulation of shale gas resources/reserves estimation in China[J].Petroleum Geology and Recovery Efficiency,2015,22(1)：1-4.

[2] 陈元千,周 游,李秀峦,等.利用SAGD开采技术预测重质油藏可采储量新方法[J].特种油气藏,2015,22(6):85-89.

Chen Yuanqian,Zhou You,Li Xiuluan,et al.A new method of using SAGD exploitation technique to predict the recoverable reserves of heavy oil reservoir[J].Special Oil & Gas Reservoirs,2015,22(6)：85-89.

[3] 杨双,闫相宾,刘志鹏,等.多层圈闭资源量计算方法研究:以两层圈闭为例[J].石油实验地质,2016,38(5):698-702.

Yang Shuang,Yan Xiangbin,Liu Zhipeng,et al.Resource calculation methods for multilayer traps:Case study of two-layer traps[J].Petroleum Geology & Experiment,2016,38(5):698-702.

[4] 杜殿发,付金刚,周志海,等.页岩气藏采收率计算方法探讨[J].特种油气藏,2015,22(5):74-77.

Du Dianfa,Fu Jingang,Zhou Zhihai,et al.Research on calculation Methodsfor recovery factor of shale gas reservoirs[J]. Special Oil & Gas Reservoirs,2015,22(5)：74-77.

[5] 石创,徐思煌,拜文华,等.湖北及周缘五峰组—龙马溪组页岩气资源潜力[J].特种油气藏,2015,22(6):65-69.

Shi Chuang,Xu Sihuang,Bai Wenhua,et al.Shale gas resource potential of Wufeng-Longmaxi Formations in Hubei and its periphery[J]. Special Oil & Gas Reservoirs ,2015,22(6)：65-69.

[6] 谢寅符,陈和平,马中振,等.概率法油气储量评估及其与确定法的差异比较[J].石油实验地质,2014,36(1):117-122.

Xie Yinfu,Chen Heping,Ma Zhongzhen,et al.Probabilistic estimation of reserves and difference between probabilistic and determine methods[J].Petroleum Geology & Experiment,2014,36(1):117-122.

[7] Bailey W, Cou⊇t B, Lamb F,et al.Taking a calculated risk[J].Oilfield Review,2000(3):20-35.

[8] Jonkman R M,Bos C F M,Breunese J N,et al.Best practices and methods in hydrocarbon resource estimation,production and emissions forecasting,uncertainty evaluation and decision making[R].SPE 65144,2000.

[9] 贾承造.美国SEC油气储量评估方法[M].北京:石油工业出版社,2004.

Jia Chengzao.SEC estimation approach for oil & gas reserves[M].Beijing:Petroleum Industry Press,2004.

[10] US Securities and Exchange Commission.Compliance and disclosure interpretation:Oil and gas rules[S].Washington,DC:SEC,2013.

[11] SPE.Canadian oil and gas evaluation handbook,Volume 2[M].Washington,DC:SPE,2005.

[12] 文环明,肖慈珣,李薇,等.蒙特卡洛法在油气储量估算中的应用[J].成都理工学院学报,2002,29(5):487-492.

Wen Huanming,Xiao Cixun,Li Wei,et al.Applications of the Monte-Carlo method to the petroleum reserves estimation[J].Journal of Chengdu University of Technology,2002,29(5):487-492.

[13] 黄学斌,李军,闫相宾,等.圈闭资源量参数概率分布及有效性检验[J].石油与天然气地质,2014,35(4):577-584.

Huang Xuebin,Li Jun,Yan Xiangbin,et al.Probability distribution of parameters for trap resources assessment and its validation[J].Oil & Gas Geology,2014,35(4):577-584.

[14] 杨振海,程维虎,张军舰.拟合优度检验[M].北京:科学出版社,2011:1-36.

Yang Zhenhai,Cheng Weihu,Zhang Junjian.Goodness of fit test[M].Beijing:Science Press,2011:1-36.

[15] 吴义平,田作基,童晓光,等.基于储量增长模型和概率分析的大油气田储量增长评价方法及其在中东地区的应用[J].石油学报,2014,35(3):469-479.

Wu Yiping,Tian Zuoji,Tong Xiaoguang,et al.Evaluation method for increase of reserves in large oil-gas fields based on reserves growth model & probability analysis and its application in Middle East[J].Acta Petrolei Sinica,2014,35(3):469-476.

[16] 涂乙,邹海燕,孟海平,等.页岩气评价标准与储层分类[J].石油与天然气地质,2014,35(1):153-158.

Tu Yi,Zou Haiyan,Meng Haiping,et al.Evaluation criteria and classification of shale gas reservoirs[J].Oil & Gas Geology,2014,35(1):153-158.

[17] 王代国.致密岩性气藏储量评价和计算方法问题与对策:以鄂尔多斯盆地大牛地气田上古生界气藏为例[J].石油实验地质,2012,34(5):495-498.

Wang Daiguo.Problem and countermeasure of reserve estimation and calculation of tight lithologic gas reservoir:A case study in Upper Paleozoic gas reservoir in Daniudi Gas Field of Ordos Basin[J].Petroleum Geology & Experiment,2012,34(5):495-498.

[18] 赵文智,毕海滨.浅析中国与西方在储量计算中确定有效厚度之差异[J].石油勘探与开发,2005,32(3):125-129.

Zhao Wenzhi,Bi Haibin.Differences of net pay estimation between China and SEC[J].Petroleum Exploration and Development,2005,32(3):125-129.

[19] Beha A,Christensen J E,Young R.A general method for the consistent volume assessment of complex hydrocarbon traps[J].Journal of Petroleum Geology,2012,35(1):85-97.

[20] 薛国勤,余强,赵创业,等.SEC准则递减曲线法在储量评估中的应用:以王集油田为例[J].石油实验地质,2012,34(5):531-534.

Xue Guoqin,Yu Qiang,Zhao Chuangye,et al.Application of diminishing curve method in SEC standard evaluation of oil and gas reserves:A case study in Wangji Oil Field[J].Petroleum Geology & Experiment,2012,34(5):531-534.

[21] 郑昊,王家华.基于多线程技术的储量分析系统构建[J].西安石油大学学报(自然科学版),2009,24(6):91-94.

Zheng Hao,Wang Jiahua.Reserves system building based on the analysis of multi-thread technology[J].Journal of Xi’an Shiyou University (Natural Science Edition),2009,24(6):91-94.

[22] 盛秀杰,金之钧,肖晔,等.圈闭评价中含油气性风险依赖性的概念、方法及应用[J].石油与天然气地质,2015,36(1):154-161.

Sheng Xiujie,Jin Zhijun,Xiao Ye,et al.Concept,method and application of geological risk dependency indicating petroleum discovery[J].Oil & Gas Geology,2015,36(1):154-161.

[23] 李洪玺,张培军,代琤,等.美国PRMS与SEC两种油气储量准则差异分析[J].西南石油大学学报(自然科学版),2016,38(5):75-80.

Li Hongxi,Zhang Peijun,Dai Cheng,et al.Difference analysis of oil & gas reserve rule between PRMS and SEC in U.S.[J].Journal of Southwest Petroleum University (Science & Techno-logy Edition),2016,38(5):75-80.

[24] 陈元千,郝明强,李飞.油气资源量评估方法的对比与评论[J].断块油气田,2013,20(4):447-453.

Chen Yuanqian,Hao Mingqiang,Li Fei.Comparison and review of the estimating methods of oil and gas resources[J].Fault-Block Oil & Gas Field,2013,20(4):447-453.

[25] 景爱霞.准噶尔盆地石油探明储量参数分析[J].石油实验地质,2012,34(5):486-489.

Jing Aixia.Analysis of proved reserve parameters of Junggar Basin[J].Petroleum Geology & Experiment,2012,34(5):486-489.

[26] 王静伟,计秉玉,张文彪.基于多因素的油田可采储量不确定性分析[J].中国海上油气,2016,28(4):76-82.

Wang Jingwei,Ji Bingyu,Zhang Wenbiao.Uncertainty analysis of oilfield recoverable reserves based on multi-factors[J].China Offshore Oil and Gas,2016,28(4):76-82.

(编辑 徐文明)

Probability distribution of reservoir parameters in the B oil field, Pearl River Mouth Basin

Tu Yi, Yang Jiao, Wang Xiuling, Wan Jun

(ShenzhenBranch,CNOOC(China)Ltd.,Shenzhen,Guangdong518000,China)

A block of the Pearl River Mouth Basin has a large trap area, irregular structure and limited well data and thus to get accurate reserve size, potential and risk, the probability method is most effective for rapid reserve assessment. The Z5 reservoir in the B oil field was taken as an example. Considering steep wings, long middle transition zone and the low level of well control, an area/thickness/shape factor method was used to construct a physical model of bulk-volume rock.Nmodules were divided according to the distribution form of reservoir. The form of Z5 reservoir was precisely described according to each module, which could reduce the influence of irregular structural form on reserve. Logarithmic normal distribution was used to analyze effective thickness and porosity. Normal distribution was chosen for oil saturation. A single value distribution model was adopted to study oil-bearing area, volume coefficient and crude oil density. The probability distribution of various reserve parameters and a reserve probability distribution model were established. The results show that thePmeanreserves of the approximate method were close to those of the deterministic method, and the error between them was less than 4%. Combined with reserve sensitivity analysis results of the geological parameters, the study could guide the studies of reserve sensitivity, economics, risk and potential, and provide a theoretical basis for development plans and decisions.

probability distribution; reserve parameter; reserve calculation; Pearl River Mouth Basin

1001-6112(2017)04-0573-07

10.11781/sysydz201704573

2017-02-16；

2017-05-04。

涂乙(1986—)，男，硕士，工程师，从事油气开发地质、储量评价及储层建模等研究。E-mail:tuyi200605156@126.com。

国家科技重大专项“南海东部海域大中型油气田地质特征”(2011ZX05023-006-03)资助。

TE15

A