用物理摆测重力加速度的实验介绍
高文莉,周 进
(南京大学 物理实验教学中心,江苏 南京 210093)

用物理摆测重力加速度的实验介绍
高文莉,周 进
(南京大学 物理实验教学中心,江苏 南京 210093)
介绍了用物理摆测量重力加速度的实验方法. 根据物理摆的简谐运动周期与摆锤到转轴之间的距离的关系,找到合适的摆锤位置,使物理摆正挂与倒挂时的振动周期值相等,从而得到比较精确的重力加速度值.
重力加速度;物理摆;简谐运动;周期
重力加速度是一个重要的地球物理常量. 在地球表面不太高的范围内,物体由于受到地球引力作用而产生的加速度,称为重力加速度. 地球上各个地区的重力加速度不仅与该地区的地理位置和相对高度有关,还与地层的结构有关. 因此,精确地测量重力加速度,在科研和生产上都有极其重要的作用[1-2]. 在经典物理条件下,有多种测量重力加速度的方法,如单摆法、自由落体法、倾斜气垫导轨法、物理摆法以及三线摆法等[3-5]. 本文主要介绍在南京大学物理实验课程中使用的物理摆测量重力加速度的方法.
1 测量原理

(1)
其中,I是物理摆绕固定轴O的转动惯量,h是质心G到转轴O的距离,m是摆的质量,g为当地的重力加速度.
对于刚体而言,其绕过质心G且与O轴平行的转轴的转动惯量IG是固定的,则由平行轴定理可知:
I=IG+mh2,
(2)
从而有
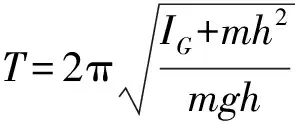
(3)
根据(1)式或(3)式,可设计多种不同的实验方案来测量重力加速度g.
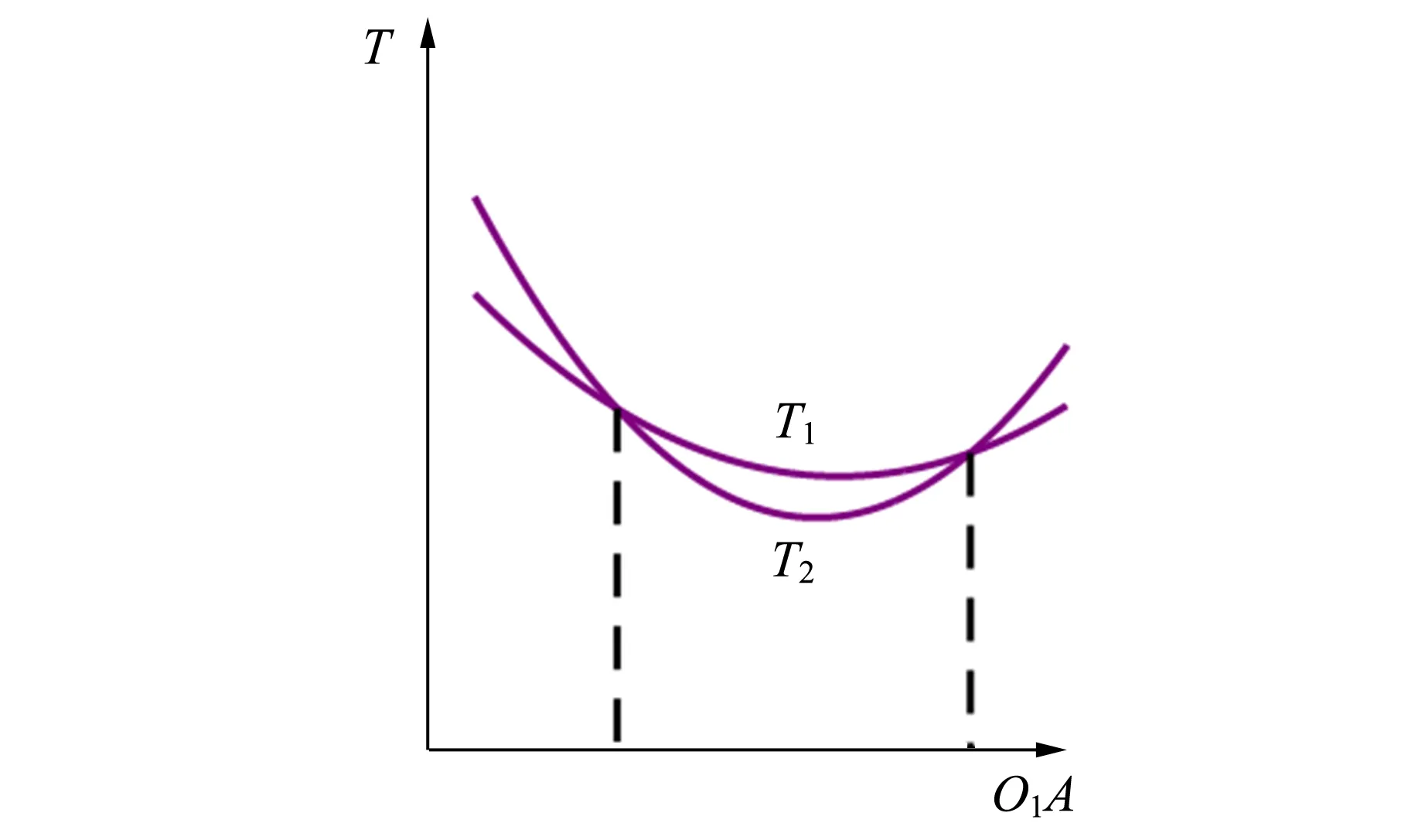
本实验主要采用带有刻度线的均质摆杆和2个不同质量的摆锤A和B组成物理摆(如图1所示),摆动周期用多功能微秒计DHTC-1来测量. 在摆角较小时,以O1为轴转动时其周期T1为
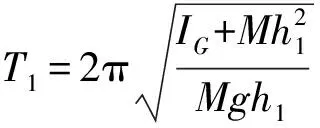
(4)
式中,M为摆的总质量,h1为转轴O1到摆的质心G的距离.
又当以O2为转轴摆动时,其周期T2为
土狼是这一带山林中最凶残的动物之一。它们成群而动,最喜攻击弱小、落单的猎物。单个的土狼并不可怕,但它们总是集结成一群协同狩猎,少则十数只,多则几十只,便是猛虎野猪,也不愿轻易招惹它们。

(5)
式中,h2为O2到G的距离. 由(4)~(5)两式得:

图1 物理摆
(6)
适当地调节摆锤A和B的位置,可使T1=T2,令此时的周期值为T,则

(7)
(7)式中h1+h2,即O1O2间的距离,设为l,则

(8)
由(8)式可知,测出物理摆正挂与倒挂时相等的周期值T和l,就可算出当地的重力加速度. (8)式中l为2个转轴之间的距离,可很精确地测得,所以能使测量g值的准确性提高.
基于此,本实验通过改变摆锤A的位置,即O1A=x的值,来研究T1和T2的变化规律,从而找到T1=T2的周期值.
2 实验方法
先在摆杆上设定2个转轴O1和O2的位置,测量l=O1O2,然后将摆锤A置于两者的中间位置,摆锤B置于O2外侧的中间,分别测T1和T2,若满足T1>T2,则摆锤A移到靠近O2处(B不动),再测T1和T2,若满足T1 1)确定摆锤B的位置 实验中所用摆杆上刻度线示数范围为-32~32 cm. 先将O1设于杆上标线31 cm处,O2设于杆上标线-14 cm处,即l=45 cm. 经调试,发现当摆锤B置于-25 cm处时,可满足当摆锤A置于O1O2中间时T1>T2,当摆锤A靠近O2时T1 2)将摆锤B置于-25 cm处,改变摆锤A的位置,测量T1曲线和T2曲线. 测得的数据列于表1中(其中T1,T2是测量15个周期后求得的平均值). 表1 摆锤A处于不同位置=O1A时相应的T1和T2值 根据表1数据,绘制出T1曲线和T2曲线如图2所示. 图2 物理摆正挂和倒挂时的T1曲线和T2曲线 拟合出的2条曲线的交点所对应的周期值即为所求. 由图2可知: T1=T2=T=1.345 s , 则 本实验是在大一下学期开设的,学生对刚体的概念有了一定的认识,对原理的理解没有太大的困难. 教师在讲解原理时可与单摆的简谐运动相类比,引导学生分析两者的异同点. 实验原理中多次用到平行轴定理,可加深学生对平行轴定理的内容和应用条件的进一步理解. 本实验主要给出了找T1=T2的方法,其中摆锤B的位置的确定非常重要,它决定了T1曲线和T2曲线能否相交,这一点需要在教学过程中重点强调. 由理论分析可知,摆锤B距O2点过近或过远,都会导致T1曲线和T2曲线不能相交(图3),也就无法用此法测量重力加速度. (a)O1B偏小 (b)O2B适中 (c)O2B偏大图3 B锤位置对T1曲线和T2曲线形状的影响 每次摆动的起始角度要保持一致,同时使摆动在铅直平面内进行,避免出现圆锥摆. 为了进一步提高测量的精度,还可在目前实验内容的基础上,在T1曲线和T2曲线的交点附近再密集取点,使测量更精细. 在本实验方法的基础上, 还可以积极引导学生基于原理设计出不同的实验方法. 如设IG=mk2,则(3)式可变为 (9) (9)可改写为 (10) 令Th2=y,h2=x,(10)式变为线性方程,即 (11) 由此可设计如下的实验方法:用平衡法找到质心的位置,然后改变转轴的位置,测量每个h所对应的简谐运动周期T,从而得到一系列的(x,y),用作图法得到直线的截距和斜率,进而求得重力量加速度. 这种方法实验操作和数据处理都比较简单,也不需要摆锤,只要测出摆杆质心的位置,然后改变转轴的位置测量周期即可. 实验采用的方法主要考虑可更全面地培养学生的实验操作技能和数据处理等综合能力,且二转轴之间的距离和振动周期都能测量得很精确,提高了所求的重力加速度值的准确性. 用物理摆测重力加速度实验原理简明易懂,有利于教师引导学生设计多种不同的实验方案,培养学生的实验素养. 该实验还可以进行拓展,用来测量物体的转动惯量或验证平行轴定理等,进一步丰富实验内容. [1] Peters A, Chung K Y, Chu S. Measurements of gravitational acceleration by dropping atoms [J]. Nature,1999, 400(6747): 849-852. [2] Mcguirk J M, Foster G T, Fixler J B, et al. Sensitive absolute-gravity gradiometry using atom-interferometry [J]. Phys. Rev. A, 2001, 65(3):184. [3] 苏为宁,王思慧,高文莉,等. 大学物理实验(理科)(第二册)[M]. 南京:南京大学出版社,2014. [4] 吕斯骅,段家忯. 新编基础物理实验[M]. 北京:高等教育出版社,2006. [5] 张兆奎,缪连元,张立,等. 大学物理实验(第四版)[M]. 北京:高等教育出版社,2016. [责任编辑:尹冬梅] Measuring the gravitational acceleration using physical pendulum GAO Wen-li, ZHOU Jin (School of Physics, Nanjing University, Nanjing 210093, China) The experiment of measuring the gravitational acceleration using physical pendulum was introduced. Based on theoretical analysis, the relationship between the harmonic oscillation period and the distance from the bob to the pivot was obtained experimentally. When properly locate the two bobs on the pendulum, an equal period could be found with the pendulum hanging right way up or upside down, which could be used to calculate a more accurate value of the gravitational acceleration. gravitational acceleration; physical pendulum; harmonic oscillation; period 2017-05-16 高文莉(1968-),女,江苏连云港人,南京大学物理学院讲师,硕士,从事物理实验及理论教学工作. 周 进(1959-),男,江苏扬中人,南京大学物理学院教授,硕士,从事物理实验及理论教学. O313.3 A 1005-4642(2017)07-0032-033 数据记录及处理

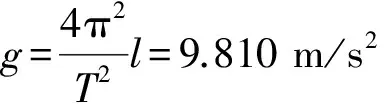
4 问题与讨论