PREM:A parallel package for finding travelling wave solutions to nonlinear evolution equations
ZHANG Zhi-an,LIU Yin-ping
(Department of Computer Science and Technology,East China Normal University,Shanghai 200062,China)
PREM:A parallel package for finding travelling wave solutions to nonlinear evolution equations
ZHANG Zhi-an,LIU Yin-ping
(Department of Computer Science and Technology,East China Normal University,Shanghai 200062,China)
In this paper,a new parallel algorithm and its implementation called PREM for solving nonlinear evolution equations are presented.PREM is developed in Maple 18. By using parallel and load balancing techniques,PREM is more effi cient than any previous serial programs.Furthermore,for some complicated equations that serial programs failed to solve,PREM may obtain some exact traveling wave solutions by factoring algorithm and time limit.In addition,the interface and output of PREM is flexible and diverse.More types of exact travelling wave solutions could be obtained by using this parallel program.
nonlinear evolution equation;travelling wave solutions;Riccati equations methods;parallel algorithm;load balance
0 Introduction
Mathematical modelling of physical systems often leads to nonlinear evolution equations. The explicit solutions of such equations are of fundamental importance for they may give more insights into internal aspects of nonlinear problems.In particular,there is considerable interest in seeking exact traveling wave solutions of nonlinear evolution equations.Rapid development of computer science and symbolic computation softwares not only allow us to perform some complicated and tedious algebraic calculations on a computer,but also help us to find new exact solutions ofnonlinear diff erentialequations.Some straightforward algebraic methods for searching exact travelling wave solutions of nonlinear evolution equations have become more and more attractive,for instance,the tanh-method[1]and its various modifications or extensions[2-3],various elliptic function expansion methods[4-6],the multiple exp-function method[7-8],etc.These methods can be easily algorithmized and mechanized.Some programs have been developed to automatically deliver solitary wave solutions ofnonlinear evolution equations,such as the Mathematica package ATFM developed by Parkes and Duff y[1]and the Maple packages RATH[9], RATHS[10]developed by Li and Liu.Similarly,the Maple package AJFM[11]can automatically deliver periodic wave solutions of nonlinear evolution equations,the Mathematica package PDESpecialSolutions.m[12]and the Maple package RAEEM[13]can automatically deliver diff erent types of travelling wave solutions of nonlinear evolution equations.In addition,the package TWSolutions embedded in Maple can be used to solve autonomous PDEs that are rationaland nonlinear in the unknowns and their derivatives,this package can deliver closed form solutions expressed as a finite power series of one of a particular set of functions(default is the hyperbolic tangent function).It should be noted that all coeffi cients of a polynomial being zero is just a suffi cient condition for a polynomial being zero,while it is not a necessary condition for that. Therefore,any one of the above mentioned algorithms or softwares is not completely covered by another.In addition,in the symbolic calculation process,the intermediate expressions expanded rapidly,any program mentioned above may fail to solve some complicated nonlinear evolution equations.The aim of this paper is to develop a parallel computing software named PREM(parallel Riccati equations methods)for the automated derivation of exact traveling wave solutions of nonlinear evolution equations.Our algorithm is based on three diff erent Riccati equations methods to construct exact travelling wave solutions of nonlinear evolution equations.By repeatedly using the parallel computation in the program,the calculation efficiency of PREM is obviously improved.Meanwhile,for a complicated nonlinear algebraic equations generated in our algorithm,PREM may deliver some but not all exact solutions by factoring and computing it in the parallel way,while in this case the existing serial programs may not output any results because of the unsolvable complicated branches.Besides,more types of exact traveling wave solutions are obtained from our program.Furthermore,to use all of the CPUs more effi ciently,a simple but eff ective greedy algorithm is designed in this paper to balance workloads of each CPU used.
Parallel computing is one of the hot issues in the field of computer science.Based on parallel computing,some new technologies have been born,such as Cloud Computing[14-15], GPU parallel computing technology[16],etc.Parallel computing has been applied to manyacademic fields,such as parallel genetic algorithm[17],machine learning[18-19],computational mathematics[20],etc.Within the field of computational mathematics,parallel computing has been applied to solve many problems,such as automated reasoning[21],linear equations system[22],combinatorial mathematics[23],proof of inequality[24],matrix operation[25],numerical calculation[26],etc.Maple provides two models for multi-threaded programming,the Task Programming Model and the Grid Programming Model.The Task Programming Model is a high-levelmulti-threaded programming model.It is designed to allow Maple code to be written that takes advantage of multiple processors,while avoiding much of the complexity of traditionalmulti-threaded programming.One thing to note here is that only“Thread-Safe”function can be used inside this programming model for its shared-memory feature.The Grid package allows users to launch multiple copies of Maple’s computation engine.Each copy of the engine is independent,thus they do not share memory as in the Task Programming Model.This means if the engines need to share data they must communicate by sending messages back and forth. As for us,we tend to use the Task model(Task Programming Model)for its simplicity and memory sharing.However,during the process of programming,we found that some built-in function of Maple are not“Thread-Safe”,such as“solve”,which means they cannot be used in the Task model.So we applied Grid model to several part sections of our program where thread-unsafe functions existed,which split our program into several sub procedures.
The paper is organized as follows.The Riccati equations and the basic ideas of the Riccati equations methods are outlined in Section 1.In Section 2,the key skills for parallel implementation of the above algorithm are expounded.The parallel program PREM and its applications are shown in Section 3.In the last section,a summary and conclusion are given.
1 The Riccatiequations and the Riccati equations methods
In this section,we first briefly outline the Riccati equations and their special solutions, and then describe the basic ideas of the Riccati equations methods.
1.1 The Riccati equations and their special solutions
The algorithm in the next subsection is based on the following three different Riccati equations and their specialwave solutions.
1.The single Riccatiequation is in the form of

in which R=±1,µ=±1.
To our knowledge,when R=±1,µ=R,Eq.(1.1)has specialsolutions
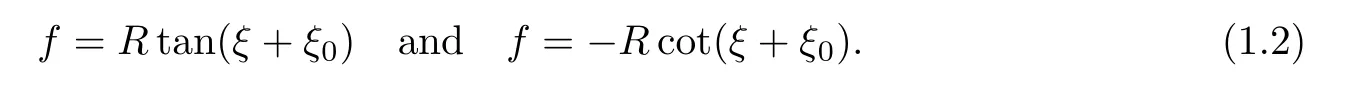
Similarly,when R=±1,µ=−R,Eq.(1.1)has special solutions

To demonstrate our algorithm and program more clearly,we named them as“case 1”and“case 2”,respectively.
2.The coupled Riccati equation has the form of

where R=±1,µ=±1.
As we know,when R=1,µ=−1,Eq.(1.4)has a group of solution

Similarly,when R=1,µ=1,Eq.(1.4)has a group of solution

When R=−1,µ=−1,Eq.(1.4)has 2 groups of solutions
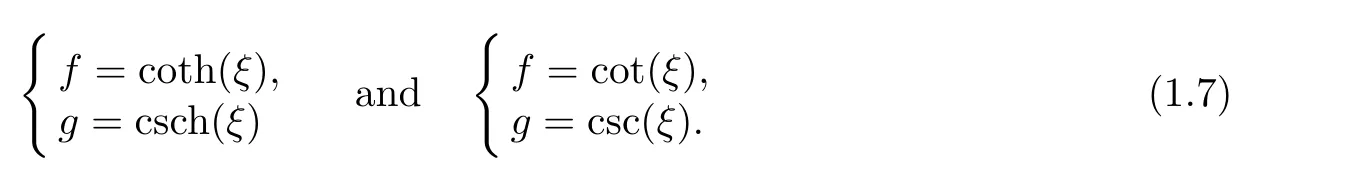
Similarly,we named them as“case 3”,“case 4”,“case 5”and“case 6”,respectively.
3.The three coupled Riccati equation is in the form of

This equation has a wave solution

where sn,cn,dn are Jacobielliptic sine,cosine and the third function,respectively.We named it as“case 7”.
1.2 The Riccati equations methods
For the sake of simplicity,we just consider a single PDE to describe the basic idea of the Riccatiequations methods.For a coupled PDE or high dimensional PDE(s),the idea is similar.
Consider a PDE

where u=u(x,t).
The basic idea of the methods to construct exact travelling wave solutions of nonlinear evolution equations are described as follows.
Step 1 Introducing a travelling wave transformationξ=kx+ct,and let u(x,t)=U(ξ), then Eq.(1.10)is transformed into an ODE

in which U(j)means the j th-order derivative of U(ξ)with respect toξ.
Step 2 Balance the order of the highest linear term with that of the highest nonlinear term,the solution order m will be determined.We should note that for a coupled nonlinear evolution equation,we may get several groups of solution orders.
Step 3 Assume the required solution is expressed as a finite series of the solutions of the Riccati equations,such as for the single Riccati equation(1.1),the corresponding solution assumption reads

in which f is a solution of the Riccati equation(1.1)and ai,i=−m,···,m,are variables to be determined later.
For the coupled Riccatiequation(1.4),the solution assumption could be expanded as

where{f,g}is a group of solution of the coupled Riccati equation(1.4).Even for the three coupled Riccati equation(1.8),the solution assumption could be expanded as

where{f,g,h}is a group of solution of the three coupled Riccatiequation(1.8).
Step 4 Substitute a solution assumption and the corresponding Riccatiequation into the ODE(1.11),a polynomialequation P(f)=0 or P(f,g)=0 or P(f,g,h)=0 willbe established. Letting the coeffi cients ofdifferent power terms in the polynomialbe zero,a nonlinear algebraic equations for ai,bj,···are obtained.
Step 5 Solve the obtained nonlinear algebraic equations,if it has nontrivial solutions, returning to the original variables we will get exact travelling wave solutions of Eq.(1.10).
2 The key skills for parallel implementation of the above algorithm
The methods described in Section 1 are algorithmic and could be easily implemented.In this paper,we implement the algorithm in parallel.The key skills are shown below.
2.1 The parallelization of the algorithm
To implement the algorithm described in Section 1,three diff erent levels of parallelism are considered as follows.
1.The above steps 1,2 are exactly the same for the three Riccati equations methods,and a single function is written to implement these two steps in series.For the coupled nonlinear evolution equation,from the step 2 we may get several groups of solution orders.For each group of solution orders,the subsequent calculation steps are similar.This is the first level of parallelism in our algorithm.We implement them in parallel by using the Task Programming Model in Maple 18.
2.For each group of solution orders,the basic ideas and procedures of the three Riccati equations methods are similar,we implement the above steps 3 and 4 in parallel for the three methods by the Task Model.This is the second level parallelism(embedded in the first level parallelism)in our program.
3.Solving the obtained nonlinear algebraic equations is a main calculation bottleneck of the algorithm,we decompose it into a set of sub equations by factoring.Apparently,these sub equations could be solved in parallel.This is the third level of parallelism in our program.As the“solve”command is not“Thread-Safe”,both Task Model and Grid Model are employed in this level of parallelism.
The parallel structure of the algorithm is shown in Fig.1.

Fig.1 The parallel structure of the algorithm
2.2 Solve nonlinear algebraic equations in parallel
By factoring,the nonlinear algebraic equations will be decomposed into a set of sub equations which are simpler to solve.And these sub equations could be solved in parallel to improve calculating effi ciency.Furthermore,we set time limits to these tasks so that they will terminate within the specified time and print the result.For some complicated nonlinear algebraic equations which are hard to be solved directly,by factoring,grouping and time limit,some of its sub equations could be solved directly and we may obtain some of its exact solutions.
For example,let’s consider the following AES(Algebraic Equations).
When solving Eq.(2.13)directly by using the Maple command“solve”,it runs without termination.By factoring we get two sub equations from it,and one of them is solved in a short time,while the other still runs without termination.By solving the simpler sub equations weget two solutions to the original AES
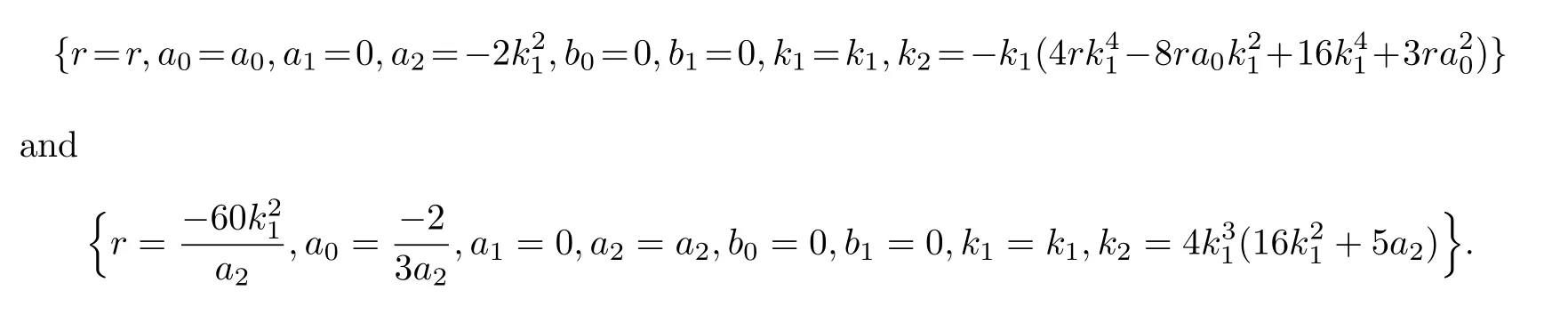
It can be seen that,for some complicated nonlinear algebraic equations which are hard to be solved directly,PREM might deliver some of its exact solutions.
2.3 Workload balance
In order to maximize the use of multicore computing,we hope to solve the sub equations mentioned above in parallel by allocating diff erent sub equations to diff erent CPU.However, for nonlinear algebraic equations obtained from the above algorithms,a factor often appears simultaneously in several different equations.By factoring,the number of sub equations may increase rapidly.For some nonlinear algebraic equations,the number of the obtained sub equations may increase to several hundreds or even more.While the number of CPU is very limited on a laptop,and the number of CPU can reach dozens on a server.Therefore,we have to divide the set of sub equations into some groups,the number of groups is usually taken as the number of CPUs.Obviously,it is important to balance the workload of each CPU in order to get the highest calculation effi ciency.How to divide the set into groups to maximize the balance of each CPU’s workload?As the highest degree of each algebraic equation in our obtained nonlinear algebraic equations is basically the same,together with the same number of equations in each sub equations.It is reasonable to take the length of a sub equations as its complexity.We take the shorter the length,the greater the priority as our greedy principle to divide the set of sub equations into groups.Then each group is allocated to a CPU,and different sub equations in this group are solved by the CPU in series.Meanwhile,different groups are executed by different CPU in parallel.
We denote the set ofsub equations as‘AESs’(array type),the number ofgroups as‘group’(integer type),and the final groups of equations sets as‘gAESs’(array type).The steps of our“group”algorithm are:
1.We first use Maple built-in function SolveTools:-Complexity()to obtain the computation complexity ofeach AES in the‘AESs’.Divide the summation ofallthe AES’s computation complexity by‘group’,we get the average computation complexity(denoted as‘avgComplexity’)of each group in the‘gAESs’.
2.Sort the‘AESs’by computation complexity in ascending order.
3.Traverse the‘AESs’,we append the AES to‘gAESs[current]’(current in[0,group-1])one by one.When‘gAESs[current]’exceeds‘avgComplexity’,we compare the last value and the current value of‘gAESs[current]’and assign the one who has smaller difference with‘avgComplexity’to‘gAESs[current]’.After that,‘current’is increased by 1.
4.When‘current’reaches group−1,the algorithm terminates.
Based on the three types of diff erent Riccati equations methods as well as the key skills described in Section 3.We have developed a parallelprogram PREMwhich could automaticallydeliver diff erent types of exact travelling wave solutions for nonlinear evolution equations.The procedures of the program are shown in the Appendix A.
3 The application of the program PREM
The interface of the program is PREM([eq],symmetric),in which eq means the equation to be solved;the parametermeans a time limit is setting to controlthe running time of the program;the parameter symmetric means an extended form or a normal form of the solution assumption is taken,that is when sy mmetric=true,the index i in(1.12) changes from−m to m,or else,the index i changes from 0 to m in(1.12).So do other solution assumptions.
In the following,two examples are given to show how to use the package and the effectiveness of our program.
Example 1 Consider the KdV equation

For this example,the program PREM is used as follows.
>PREM([diff(u(x,t),t)+6*u(x,t)*(diff(u(x,t),x))+(diff(u(x,t),x$3))=0],100,true);
For this input,PREM outputs 15 solutions within 4 seconds.
There is 1 case.
For the case{m1=2},the results are shown below.
1.Solutions obtained from the Riccati equation method


For this example,when setting’=100 and‘symmetric’=true,PREM delivered a group of solution orders{m1=1,m2=1}and 20 solutions within 9 seconds.
1.Solutions by the Riccati equation method are as follows



Compared with the existing related serial program,the program PREM not only has higher calculation effi ciency,but also may get some but not all exact solutions for some complicated nonlinear evolution equations which failed by the corresponding serial program.For the convenience to compare,a serial program is developed for completely implementing the three Riccati equations methods,too.In Appendix B,10 examples are given to compare the calculating effi ciency ofthe serialprogram and the parallelprogram PREM.It can be seen that including time spend in communications,the effi ciency of PREM rises nearly 1 time.
4 Conclusion
We have described our Maple package PREM that automates the three Riccatiequations methods for finding traveling wave solutions ofnonlinear evolution equations in parallel.It can be seen that PREM has the following advantages:(1)more types and more general solutions are delivered;(2)the solution set output is the minimum set,that is,special solutions and equivalent solutions are deleted;(3)time restriction could avoid the program from nonstop running;(4)parallelism make the program more effi cient and effective.In the near future,we willtry further to improve the code effi ciency ofthe program and apply the parallelism to other methods.
Appendix A
PREM mainly contains ten sub procedures:PREM(),GetBalancingNumber(),Par-FactorAES(),GroupAESs(),,Summarize().The outlines of the procedures are as follows.
•GetBalancingNumber(eqs)In this procedure,we first decompose the input equation(s) into components to extract unknown function name,independent variables list.Then transform the originalPDE into an ODE,and further by balancing the highest linear term with the highest nonlinear term to determine the order m of the required solution.
•FactorAES(AES,nonzero)In this procedure,our aim is to factor an AES into a set of simpler nonlinear algebraic equations.There are two parameters contained in this interface, in which the‘AES’means a nonlinear algebraic equations to be factored and the parameter‘nonzero’means nonzero parameters int the‘AES’.
•GroupAESs(AESs,group)In this procedure,all sets of nonlinear algebraic equations obtained from the procedureis to be divided into several balanced groups. The number of the groups is generally taken as the number of CPUs in the computer you are using.The parameter‘AESs’means the algebraic equations sets be grouped and the parameter‘group’means the number of the groups.
•Summarize()In this procedure we output the totalrunning time and the number of legal solutions.
Appendix B
In the following,10 examples are given to compare the calculation effi ciency of the serial program and the parallel program PREM.

Tab.1 10 examples to compare the computation effi ciency
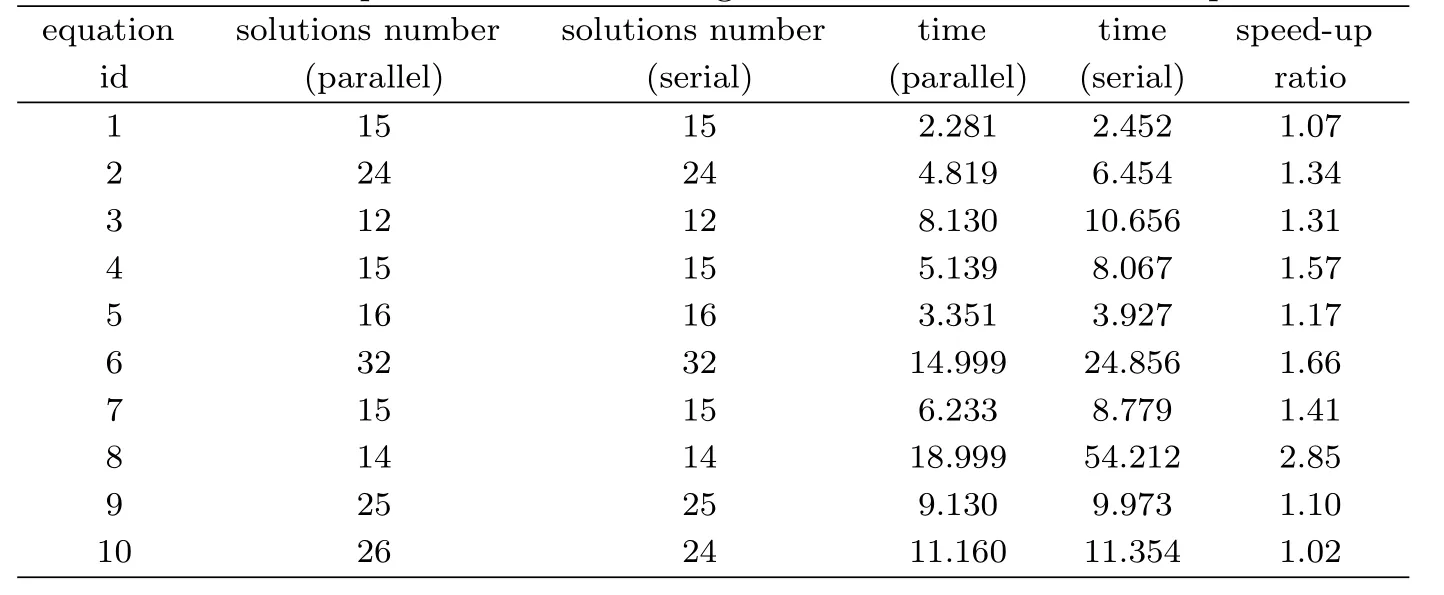
Tab.2 Comparison of the running time for the above 10 examples
[1]PARKES E J,DUFFY B R.An automated tanh-function method for fi nding solitary wave solutions to nonlinear evolution equations[J].Computer Physics Communications,1996,98(3):288-300.
[2]EL S A.Modifi ed extended tanh-function method for solving nonlinear partial diff erential equations[J].Chaos Solitons&Fractals,2007,31(5):1256-1264.
[3]ABDOU M A.The extended tanh method and its applications for solving nonlinear physical models[J].Applied Mathematics&Computation,2007,190(1):988-996.
[4]LIU S K,FU Z T,LIU S D,et al.Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations[J].Physics Letters A,2001,289:69-74.
[5]FU Z T,LIU S K,LIU S D,et al.New Jacobi elliptic function expansion and new periodic solutions of nonlinear wave equations[J].Physics Letters A,2001,290(1/2):72-76.
[6]YAN Z.The extended Jacobian elliptic function expansion method and its application in the generalized Hirota-Satsuma coupled KdV system[J].Chaos Solitons&Fractals,2003,15(3):575-583.
[7]HE J H,WU X H.Exp-function method for nonlinear wave equations[J].Chaos Solitons&Fractals,2006,30(3): 700-708.
[8]MA W X,HUANG T,YI Z.A multiple exp-function method for nonlinear diff erential equations and its application[J].Physica Scripta,2010,82(6):5468-5478.
[9]LI Z B,LIU Y P.RATH:A Maple package for fi nding travelling solitary wave solutions to nonlinear evolution equations[J].Computer Physics Communications,2002,148(2):256-266.
[10]LIU Y P,LI Z B.A Maple package for fi nding exact solitary wave solutions of coupled nonlinear evolution equations[J].Computer Physics Communications,2003,155(1):65-76.
[11]LIU Y P,LI Z B.An automated Jacobi elliptic function method for fi nding periodic wave solutions to nonlinear evolution equation[J].Chinese Physics Letters,2002,19(9):1228-1230.
[12]BALDWIN D,GOKTAS U,HEREMAN W,et al.Symbolic computation of exact solutions expressible in hyperbolic and elliptic functions for nonlinear PDEs[J].Journal of Symbolic Computation,2004,37(6):669-705.
[13]LI Z B,LIU Y P.RAEEM:A Maple package for fi nding a series of exact traveling wave solutions for nonlinear evolution equations[J].Computer Physics Communications,2004,163(3):191-201.
[14]ZHANG J X,GU Z M,ZHENG C.Survey of research progress on cloud computing[J].Application Research of Computers,2010,27(2):429-433.
[15]BERA S,MISRA S,RODRIGUES J J P C.Cloud computing applications for smart grid:A Survey[J].IEEE Transactions on Parallel&Distributed Systems,2015,26(5):1477-1494.
[16]OWENS J D,LUEBKE D,GOVINDARAJU N,et al.A survey of general-purpose computation on graphics hardware[J].Computer Graphics Forum,2007,26(1):80–113.
[17]CANT-PAZ E.A survey of parallel genetic algorithms[J].Calculateurs Paralleles Reseaux Et Systems Repartis, 1999,10(4):429-449.
[18]UPADHYAYA S R.Parallel approaches to machine learning—–A comprehensive survey[J].Journal of Parallel &Distributed Computing,2013,73(3):284-292.
[19]AGRAWAL R,SHAFER J C.Parallel mining of association rules[J].Knowledge&Data Engineering IEEE Transactions on,1996,8(6):962-969.
[20]BERGHEN F V,BERSINI H.CONDOR,a new parallel,constrained extension of Powell’s UOBYQA algorithm:Experimental results and comparison with the DFO algorithm[J].Journal of Computational&Applied Mathematics,2005,181(1):157-175.
[21]CHALABINE M,KESSLER C.A Survey of reasoning in parallelization[C]//Proceedings of the Eighth Acis International Conference on Software Engineering.IEEE Computer Society,2007(3):629-634.
[22]WING O,HUANG J W.A computation model of parallel solution of linear equations[J].IEEE Transactions on Computers,1980,29(7):632-638.
[23]LI G J,WAH B W.Computational effi ciency of parallel combinatorial or-tree searches[J].IEEE Transactions on Software Engineering,1990,16(1):13-31.
[24]HOFFMANN K H,ZOU J.Parallel solution of variational inequality problems with nonlinear source terms[J]. Ima Journal of Numerical Analysis,1996,16(1):31-45.
[25]GALIL Z,PAN V.Parallel evaluation of the determinant and of the inverse of a matrix[J].Information Processing Letters,1989,30(1):41-45.
[26]WANG WQ.A parallelalternating diff erence implicit scheme for a dispersive equation[J].Mathematica Numerica Sinica,2005,27(2):129-140.
(责任编辑:林磊)
PREM:并行求解非线性演化方程行波解的软件包
张治安,柳银萍
(华东师范大学计算机科学与技术系,上海200062)
本文提出了一种新的构造非线性演化方程行波解的并行算法.我们在Maple 18上实现了该算法.通过设计并行算法并使用负载均衡技术,其中的软件PREM的计算效率明显高于已有的串行软件.且基于因式分解算法和运行时间限制,PREM可以自动推导出一些串行程序算不动的复杂方程的部分精确解.相比于已有的其他程序,PREM可自动推导出更多类型的精确行波解.此外,PREM具有灵活的接口和输出.
非线性演化方程;行波解;Riccati方程方法;并行算法;负载均衡
2016-09-28
国家自然科学基金(11435005)
张治安,男,硕士研究生,研究方向为数学机械化.E-mail:yifanzza@163.com.
柳银萍,女,教授,研究方向为符号计算.E-mail:ypliu@cs.ecnu.edu.cn.
1000-5641(2017)04-0018-16
O175;TP311.1
A
10.3969/j.issn.1000-5641.2017.04.002

