基于极化敏感阵列的高效DOA与极化参数联合估计算法
王利伟,朱晓丹,王 建,陈 卓
(中国航天科工集团8511研究所,江苏 南京 210007)
·工程应用·
基于极化敏感阵列的高效DOA与极化参数联合估计算法
王利伟,朱晓丹,王 建,陈 卓
(中国航天科工集团8511研究所,江苏 南京 210007)
提出一种基于极化敏感阵列的二维波达方向(DOA)和极化参数联合估计算法。首先建立入射信号模型,然后利用重构的x轴、y轴、z轴阵列导向矢量之间的关系计算出入射信号的DOA和极化参数的无模糊粗估计值;同时根据重构阵列导向矢量内在的旋转不变结构估计出x轴和y轴空间相移因子,得到入射信号的高精度无模糊DOA估计。最后利用粗估计精估计相结合的方式进行解模糊,进而完成DOA估计。算法允许阵元间距大于入射信号的半波长,扩展了有效阵列孔径,提高了算法的测向精度。此外,算法避免了复杂的四维谱峰搜索,具有较低的运算复杂度。仿真实验结果验证了算法的有效性和良好的估计性能。
极化敏感阵列;DOA和极化参数估计;导向矢量重构;粗估计和精估计
0 引言
极化敏感阵列能够在利用入射信号的空域信息的同时充分利用其极化信息,与传统的标量阵列相比,基于极化敏感阵列的辐射源测向可以利用极化信息进一步提高测向性能[1-3]。在相关研究中,一些传统的基于标量阵列的波达方向(DOA)估计算法已经被推广到极化敏感阵列,衍生出多种DOA和极化参数的联合估计算法[4-6]。文献[7]提出了一种长矢量多重信号分类(MUSIC)算法(简称为LV-MUSIC),具有原理简单、估计精度较高等优势,然而该算法需要四维谱峰搜索,运算量巨大,严重地限制了该算法在实际工程中的应用。为了降低运算复杂度,文献[8]提出了一种基于拉格朗日乘子原理的降维MUSIC算法,在算法实现过程中要求优化函数必须为凸函数,仍然需要进行一维谱峰搜索操作。文献[5,9]采用基于极化敏感阵列的时间旋转不变子空间(ESPRIT)类算法,要求各个入射信号间频率不能相同。文献[10]克服了文献[5,9]中算法存在的问题,提出了一种有效的一维DOA和极化参数联合估计算法。然而,上述研究算法的阵元间距均限制在入射信号的半波长以内,严重制约了算法的测向精度。
针对上述问题,本文提出一种高效的基于极化敏感阵列的二维DOA和极化参数联合估计算法,该算法采用粗估计和精估计相结合的方式进行二维DOA估计,避免了运算量繁杂的多维谱峰搜索操作。此外,在该算法中阵元间距可以远大于入射信号的半波长,扩展了有效地阵列孔径,提高了测角精度。计算机仿真实验验证了本文所提算法的有效性。
1 信号模型和阵列结构
考虑K个完全极化的远场窄带电磁波(TEM)信号入射到由M个平行于x轴、M个平行于y轴和2M个平行于z轴的电偶极子组成的均匀L型阵列,阵列构型如图1所示。其中,相邻两个电偶极子对沿x轴和y轴方向的阵元间距d均远大于入射信号的波长λ的一半,即d≫λ/2。俯仰角θ∈[0,π/2)定义为入射信号与z轴正方向的夹角,方位角φ∈[0,2π)定义为入射信号在xoy平面的投影偏离x轴正方向的角度。
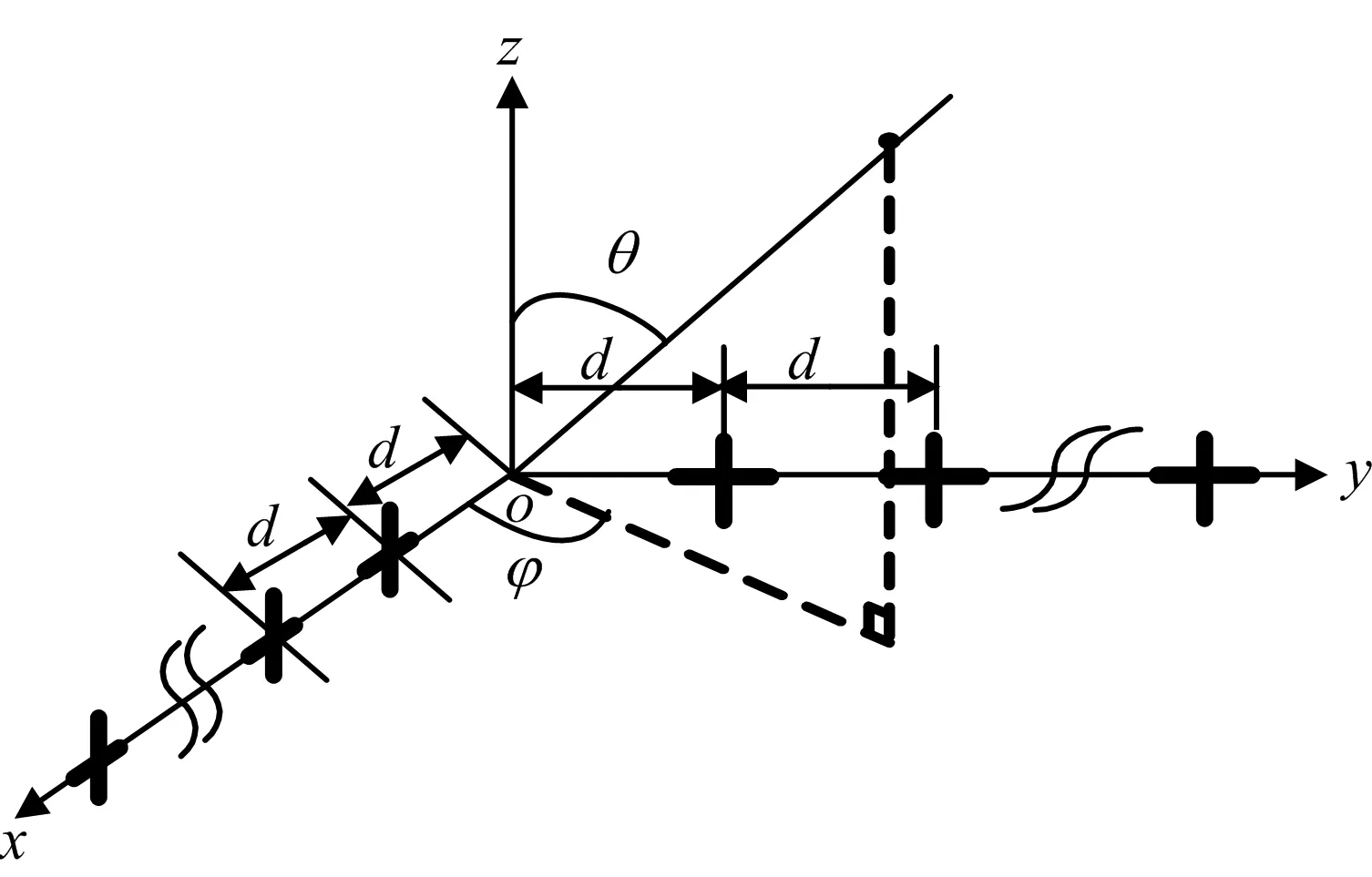
图1 均匀L型阵列
由于该阵列中每个阵元均由正交偶极子对构成,那么x轴和y轴方向的极化域导向矢量可以分别表示为:
(1)
(2)
式中,γ∈[0,π/2)表示极化辅助角,η∈[-π,π)表示极化相位差。根据该阵列结构,x轴和y轴方向的空域导向矢量分别为:
(3)
(4)
式中,qx,k=ej2πukΔx/λ定义为入射信号沿x轴方向的空间相位因子,qy,k=ej2πvkΔy/λ定义为入射信号沿y轴方向的空间相位因子,uk=sinθkcosφk表示入射信号沿x轴方向的方向余弦,vk=sinθksinφk表示入射信号沿y轴方向的方向余弦。
结合式(1)~(4),整个L型均匀线阵的导向矢量可以写成:
(5)
式中,⊗表示Kronecker积。在t时刻,整个阵列接收数据矢量可以表示成:
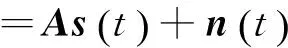
(6)
式中,A=[a(φ1,θ1,γ1,η1),a(φ2,θ2,γ2,η2),…,a(φK,θK,γK,ηK)]定义为阵列流型矩阵,s(t)=[s1(t),s2(t),…,sK(t)]表示信号矢量,n(t)为高斯白噪声。考虑多快拍情况下,阵列接收数据表示为:
X=AS+N
(7)
式中,X=[x(1),x(2),…,x(L)],S= [s(1),s(2), …,s(L)],N= [n(1),n(2),…,n(L)],L为快拍数。本文所提算法的目标为估计K个目标辐射源(φ1,θ1,γ1,η1),(φ2,θ2,γ2,η2),…,(φK,θK,γK,ηK)的DOA和极化参数。
2 算法描述
根据式(7),X的协方差矩阵可以表示为:
(8)
对矩阵R进行特征值分解(EVD),可以得到K个较大特征值和2M-K个较小特征值,然后,利用K个较大特征值对的特性向量构建信号子空间矩阵Es。由文献[11]可知,子空间矩阵Es的列向量与阵列流型矩阵A的列向量张成同一子空间,因此一定存在一个满秩矩阵T满足:
(9)
式中,Δx=diag{qx,1,qx,2,…,qx,K}和Δy=diag{qy,1,qy,2,…,qy,K}分别表示由x轴和y轴方向的空间相位因子构成的K×K维对角阵;Cx,z=[cx,1,cx,2,…,cx,K]和Cy,z=[cy,1,cy,2,…,cy,K]分别由x轴和y轴方向的极化域导向矢量构成。
根据图1中的阵列构成,将Es分割成4个大小相同的子矩阵:
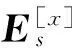
(10)
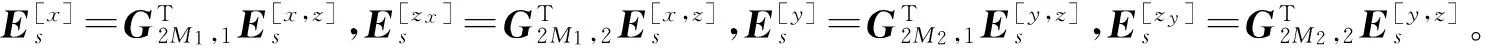
Gm,n=[gn,gn+2,…,gn+m-2],n=1,2
(11)

(12)
(13)
式中,Jm,n=[0(l-1)×(n-1)I(l-1)0(l-1)×(2-n)]为选择矩阵。根据式(12)和式(13),有:
(14)
那么,阵列流型矩阵A的估计值为:
(15)
(16)
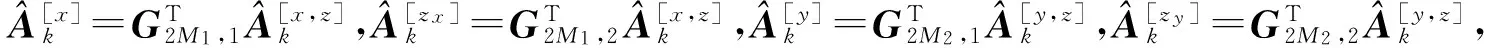
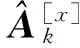
(17)
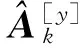
(18)
然后,根据式(17)和(18)可以得到目标辐射源的方位角、俯仰角、极化辅助角和极化相位差的粗估计结果:
(19)
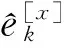
(20)

(21)
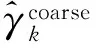
(22)
对于实际被动测向系统来说,精确的DOA估计结果是准确探测目标雷达的必要条件。相比之下,极化参数估计结果可以用来判断目标辐射源的极化方式或者用来区分目标雷达和诱饵,因此其估计精度则不需要非常精确。由式(19)~(22)可知,粗估计结果与阵元间距无关,这使得目标辐射源的DOA粗估计结果的估计精度不高,但是估计结果中不存在模糊值。下面通过估计与阵列孔径相关的空间相移因子实现更精确的DOA估计。
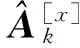
(23)
(24)
根据式(23)和式(24)的估计结果,进而求出x轴和y轴方向余弦的估计值。由于阵元间距满足d≫λ/2,循环模糊估计结果不可避免,因此含有循环模糊值的x轴和y轴方向余弦的精估计结果如下:
(25)
(26)
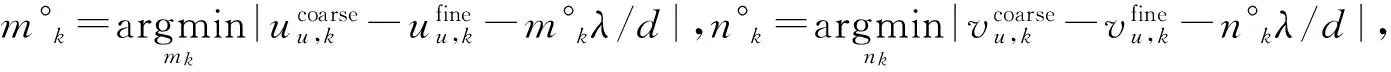
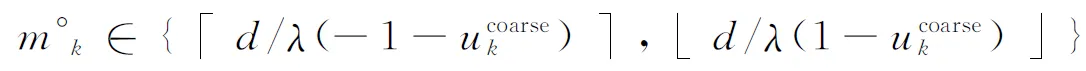
(27)
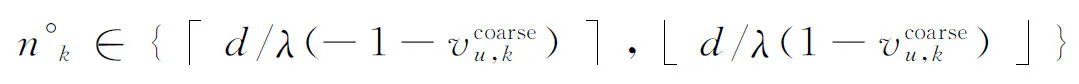
(28)

3 运算复杂度分析
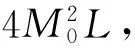
4 计算机仿真结果
本节通过计算机仿真实验来验证本文所提算法良好的测向性能,仿真平台为MATLAB 7.8 (R2009a),计算机配置为2.8GHz,4GB RAM。仿真过程中采用图1所示的8阵元的(M0=8)L型正交偶极子均匀线阵,阵元间距d=6×λ/2,仿真实验均采用200次Monte Carlo 实验。
实验1:入射信号的DOA和极化参数估计散点图
为了验证本文所提算法的有效性,该实验分别给出入射信号方位-俯仰角的粗估计、方位-俯仰角的精估计以及极化参数估计的散点图。三个入射信号的参数分别为{135.2°,15.3°,40°,80°},{33.1°,69.5°,45°,60°},{72.4°,25.3°,55°,70°},信噪比固定为10dB,快拍数固定为500。方位-俯仰角的粗估计与精估计,以及极化辅助角-极化相位差的粗估计,结果如图2~4所示。
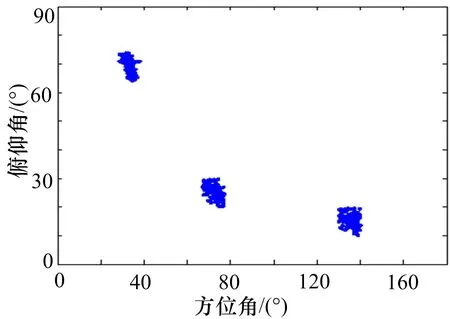
图2 方位-俯仰角粗估计结果
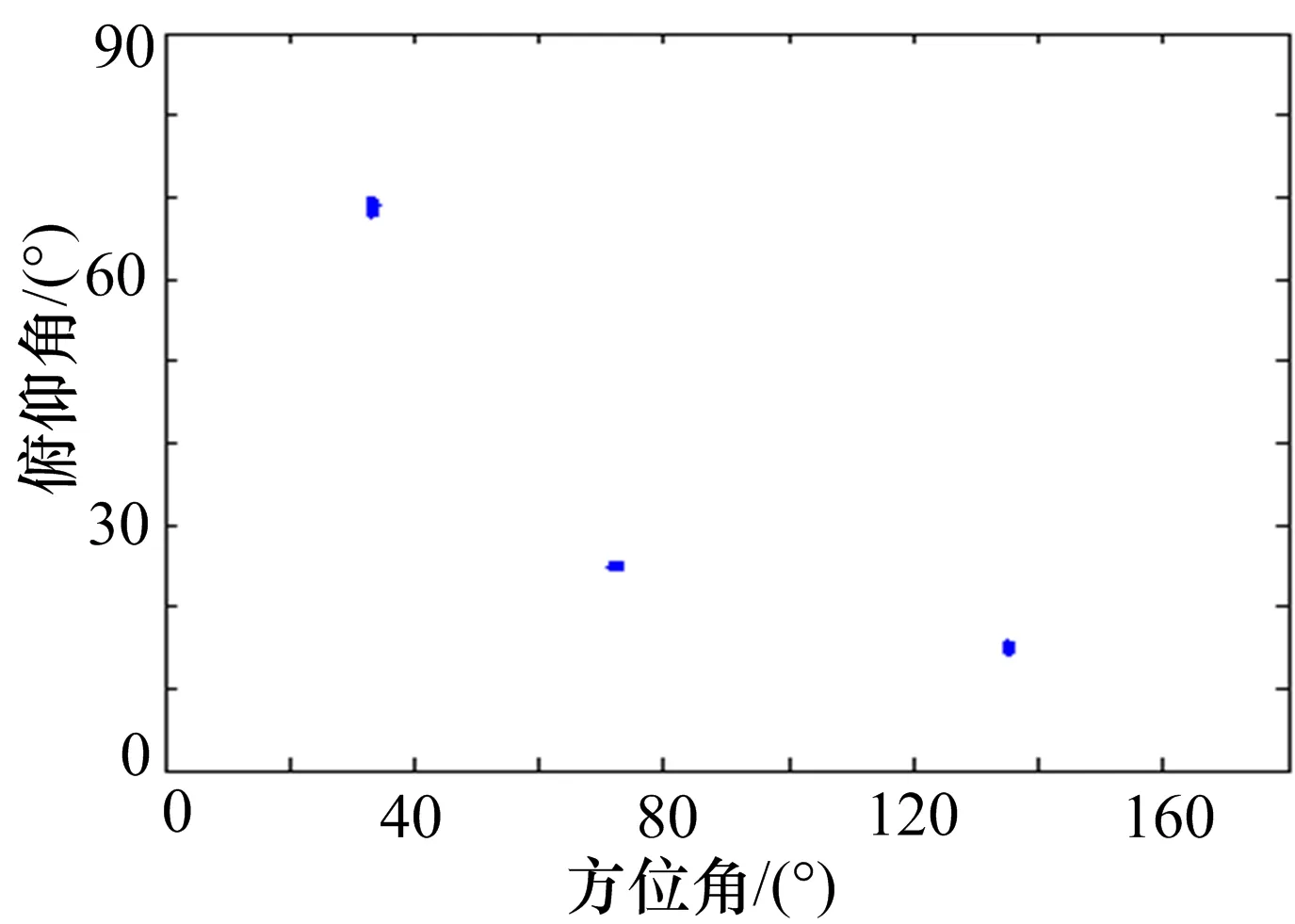
图3 方位-俯仰角精估计结果
从图2~4的仿真结果可以看出,本文所提算法能有效地估计出入射信号的DOA和极化参数,并且DOA的精估计结果要明显好于其粗估计结果。此外,极化参数的估计结果由DOA粗估计获得,因此两者估计精度相同。
实验2:DOA估计均方根误差(RMSE)随信噪比、快拍数变化曲线
为了评价本文所提算法的测向性能,该实验中选取LV-MUSIC算法作为对比算法。同时,采用方位角和俯仰角的联合均方根误差作为评价标准,其定义为:
(29)
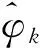
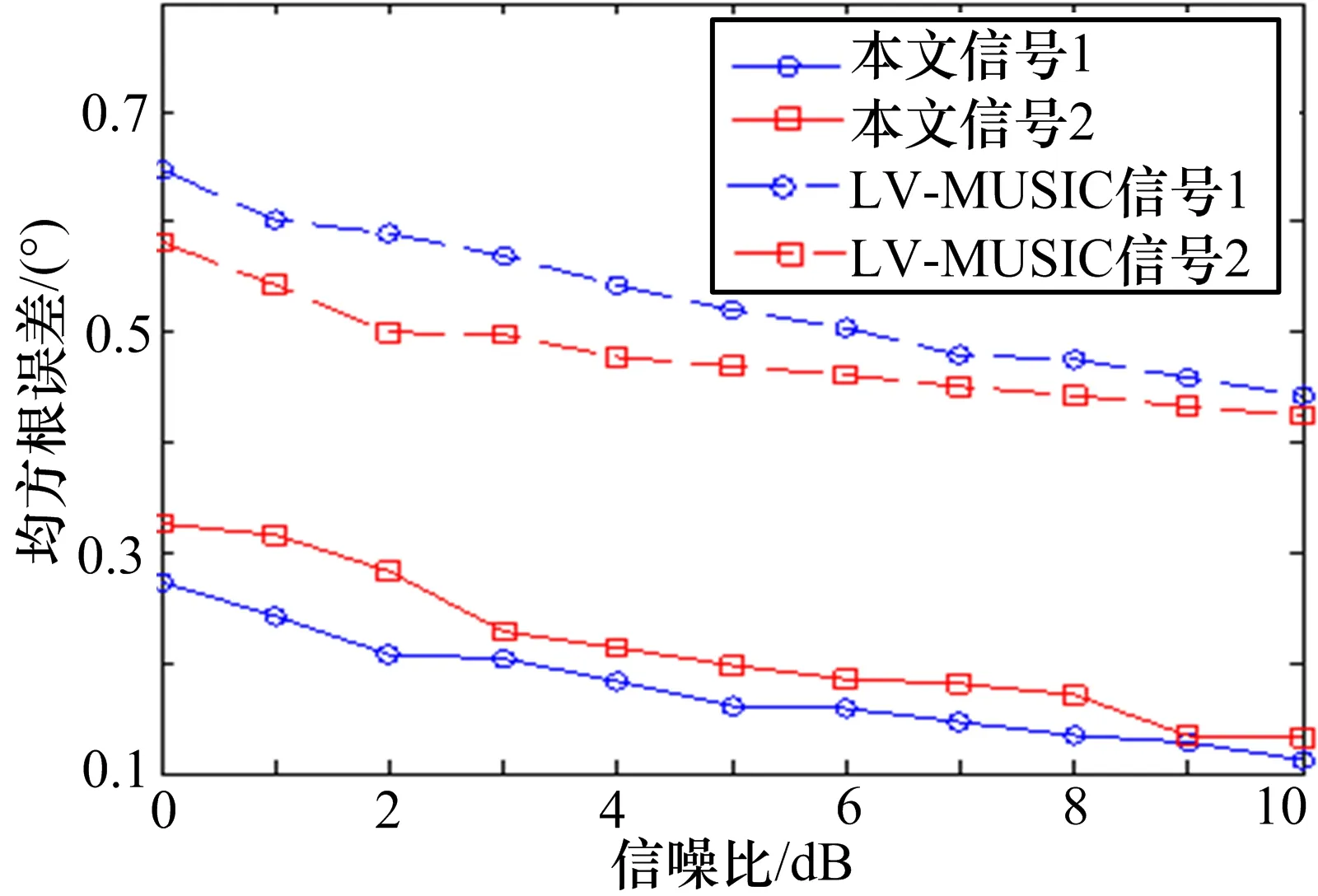
图5 均方根误差随信噪比变化曲线

图6 均方根误差随快拍数变化曲线
从图5~6中可以看出,本文所提算法的测向性能明显优于LV-MUSIC算法,这是由于所提算法采用粗估计和精估计相结合的方式实现DOA估计,并且阵元间距可以远大于入射信号半波长,扩展了有效阵列孔径。相比而言,LV-MUSIC算法采用四维谱峰搜索操作,运算复杂度较高,其测向精度受限于搜索步长。综上所述,本文所提算法具有较好的估计性能。
5 结束语
针对DOA和极化参数联合估计问题,本文采用粗估计和精估计相结合的方式给出了一种有效的算法。该算法允许阵元间距远大于入射信号半波长,在相同阵元数情况下扩展了有效阵列孔径,从而提高了算法的测向精度。此外,算法在执行过程中没有涉及多维谱峰搜索、循环迭代等运算复杂度较高的操作,因此实时性较高。计算机仿真实验验证了本文所提算法的有效性。■
[1] 徐友根,刘志文,龚晓峰.极化敏感阵列信号处理[M].北京:北京理工大学出版社, 2013:1-21.
[2] Yuan X. Estimating the DOA and the polarization of a polynomial-phase signal using a single polarized vector-sensor[J]. IEEE Trans. on Signal Processing, 2012,60(3):1270-1282.
[3] Nehorai A, Paldi E. Vector-sensor array processing for electromagnetic source localization[J]. IEEE Trans. on Signal Processing, 1994,42:376-398.
[4] Wong KT, Zoltowski MD. Self-initiating MUSIC-based direction finding and polarization estimation in spatio-polarizational beamspace[J]. IEEE Trans. on Antennas and Propagation, 2000,48(8):1235-1245.
[5] Wong KT, Yuan X. “Vector cross-product direction-finding” with an electromagnetic vector-sensor of six orthogonally oriented but spatially noncollocating dipoles/loops[J]. IEEE Trans. on Signal Processing, 2011, 59(1):160-171.
[6] Liu Z. DOA and polarization estimation via signal reconstruction with linear polarization-sensitive arrays[J]. Chinese Journal of Aeronautics, 2015,28:1718-1724.
[7] Hua Y. A pencil-MUSIC algorithm for finding two-dimensional angles and polarizations using crossed dipoles[J]. IEEE Trans. on Antennas and Propagation, 1993,41(3):370-376.
[8] Zhang X, Chen C, Li J, et al. Blind DOA and polarization estimation for polarization-sensitive array using dimension reduction MUSIC[J]. Multidimensional Systems and Signal Processing, 2014,25(1):67-82.
[9] 郑桂妹,陈伯孝,杨明磊.新型拉伸电磁矢量传感器的两维高精度波达方向估计[J].系统工程与电子技术,2014,36(7):1282-1290.
[10]Si W, Zhao P, Qu Z, et al. Computationally efficient angle and polarization estimation in the presence of multipath propagation using dual-polarization vector sensor array[J]. International Journal of Antennas and Propagation, 2016.
[11]Li J. Direction and polarization estimation using arrays with small loops and short dipoles[J]. IEEE Trans. on Antennas and Propagation, 1993,41:379-387.
Efficient DOA and polarization parameter joint estimation method based on polarization sensitive array
Wang Liwei, Zhu Xiaodan, Wang Jian, Chen Zhuo
(No.8511 Research Institute of CASIC, Nanjing 210007, Jiangsu, China)
A direction of arrival (DOA) and polarization parameter joint estimation method based on polarization sensitive array is proposed. First, the signal model based on an L-shaped crossed dipole array is built. Then, the coarse DOA and polarization estimation are derived exploiting the relationship among the reconstructed steering vectors of the signals alongx-axis,y-axis andz-axis. Meanwhile, the spatial phase factors alongx-axis andy-axis are calculated by taking advantage of the inherent rotational invariance structure of the reconstructed steering vectors, with which the fine and ambiguous estimates of DOA are achieved. Finally, the coarse DOA estimation serve as coarse references to disambiguate, leading to the fine and unambiguous estimates of DOA. In the proposed method, the adjacent array elements’ spacing is allowed beyond half wavelength of the signal, which extends the effective array aperture and improve the DOA estimation accuracy accordingly. Besides, the proposed method avoids the computationally expensive 4-D spectral search, thus its computational complexity is relatively low. Simulation results verify the effectiveness and favorable performance of the proposed method.
polarization sensitive array; DOA and polarization estimation; steering vector reconstruction; coarse estimates and fine but ambiguous estimates
2017-03-12;2017-05-23修回。
王利伟(1989-),男,博士,研究方向为阵列测向、目标跟踪技术。
TN975
A

