带电胶体粒子弹性有效电荷测量的理论改进∗

王林伟徐升华周宏伟 孙祉伟 欧阳文泽 徐丰

1)(北京交通大学土木建筑工程学院,北京 100044)

2)(中国科学院力学研究所,微重力重点实验室,北京 100190)

3)(中国科学院大学工程科学学院,北京 100049)

(2016年11月22日收到;2016年12月17日收到修改稿)

带电胶体粒子弹性有效电荷测量的理论改进∗

王林伟1)2)†徐升华2)3)‡周宏伟2)孙祉伟2)欧阳文泽2)徐丰1)

1)(北京交通大学土木建筑工程学院,北京 100044)

2)(中国科学院力学研究所,微重力重点实验室,北京 100190)

3)(中国科学院大学工程科学学院,北京 100049)

(2016年11月22日收到;2016年12月17日收到修改稿)

对于带高电荷的胶体粒子形成的胶体晶体,用现有的剪切模量与粒子间相互作用的理论模型去计算剪切模量时,得到的结果要比实验测量值大很多,而根据此理论模型由剪切模量测量值拟合得到的粒子表面有效电荷也比实验测量的表面有效电荷小很多.这个问题一直没有合理的解释.分析认为这是由于理论模型基于理想晶体,并没有考虑到实际晶体中存在孔隙等缺陷会造成材料机械性能的下降.针对该因素,本文对已有的理论模型进行了修正,引入了孔隙造成的影响,同时使用Sogam i-Ise相互作用势代替原来常用的Yukawa作用势.研究中用扭转共振法测量了带电粒子胶体晶体的剪切模量,比较了分别根据修正前后的关系模型由所测剪切模量拟合的有效电荷(弹性有效电荷),证实修正后的理论模型更合理,与使用A lexander等的方法得到的归一化电荷相比,一致性有了明显提高.

有效电荷,剪切模量,孔隙,胶体晶体

1 引 言

胶体粒子的水溶液分散体系在化工领域有着广泛的应用.当分散在水或者其他极性溶液中时,胶体粒子表面的反离子常发生溶解从而使胶体粒子带电[1,2].胶体粒子的带电特性影响了胶体体系的很多性质,如电泳、粒子间相互作用、胶体体系稳定性等[3−5].此外,带电粒子胶体体系还可以在一定条件下形成某种结构,如有序的胶体晶体等,而粒子的带电情况会直接影响形成的胶体晶体的弹性等宏观性质[6−8].

虽然胶体粒子表面的固有电荷(intrinsic charge,键合在粒子表面的离子化基团的总数)很容易用化学方法(如电导滴定法)直接测得,但实际上胶体粒子表面带电的情况相当复杂,在很多情况下,固有电荷并不能和体系的相关性质直接联系起来.这是因为在带电胶体粒子表面形成一种胶体-反离子的复杂结构,即反离子聚集(counterion association)现象.这一现象屏蔽了粒子的固有电荷Z,使得粒子好像表现出了一个小于固有电荷的表观电荷,叫做有效电荷Z∗(effective charge)[3,9,10].目前有效电荷的测量方法有很多,不同方法得到的有效电荷有着不同的称谓,分别如下:1)通过电导滴定法得到的叫做滴定有效电荷;2)通过电导率-数密度法得到的叫做迁移有效电荷;3)通过扭转共振法(针对胶体晶体体系)得到的叫做弹性有效电荷(eff ective elasticity charge);4)通过A lexander的平均场归一法得到的叫做平均场归一电荷.

国际上关于粒子表面有效电荷已有很多的研究,其中最早定量分析胶体晶体中胶体粒子电荷归一化方法的是A lexander等,其在W igner-Seitz(WS)球形胞格模型中数值求解Poisson-Boltzmann(PB)方程,再在胞格边界处将PB方程的Debye-Hückl线性近似式中的静电势能与非线性PB方程结果相匹配.这种利用固有电荷Z求得粒子有效电荷的方法叫作平均场归一法(mean field renormalization)[3,11,12],所得有效电荷叫作平均场归一电荷.周宏伟等[2]的研究结果表明用电导滴定法得到的滴定有效电荷和电导率-数密度法得到的迁移有效电荷相一致,差值在7%以内.而Wette等[11,13]的研究表明电导率-数密度法得到的迁移有效电荷值并不适用于估算带电粒子胶体晶体剪切模量的理论模型,因为迁移有效电荷比根据此模型拟合的弹性有效电荷大40%左右.Shap ran等[12]的研究结果表明,由扭转共振法反推得到弹性有效电荷和由平均场归一法得到的平均场归一化电荷之间相差较小,在20%以内.考虑到平均场归一电荷与粒子间的相互作用相关[3],而弹性有效电荷也是通过剪切模量反推得到,其使用的理论公式也与粒子间相互作用有关[14,15],因而这两种方式得到的电荷差别较小是符合理论预期的.

然而,最近的研究显示由高电荷粒子形成的胶体晶体中往往有孔隙等缺陷存在,缺陷无疑会降低胶体晶体的机械性能[7,8,16,17].而目前弹性有效电荷的测量所使用的理论模型都以没有缺陷的理想晶体为前提,没有考虑到孔隙的影响,因而不能正确描述有孔隙存在时的胶体晶体体系的性能.针对这一问题,本文旨在修正用以拟合弹性有效电荷所使用的剪切模量-相互作用势关系式模型,在其中引入孔隙的影响,并和其他方法得到的有效电荷结果进行比较,验证我们改进的弹性有效电荷测量方法的有效性.

2 理论模型的改进

之前用于拟合弹性有效电荷的剪切模量-相互作用势关系模型是针对没有孔隙的理想的胶体晶体,其对于体心立方(bcc)和面心立方(fcc)结构的表达式分别为[11,15,18]

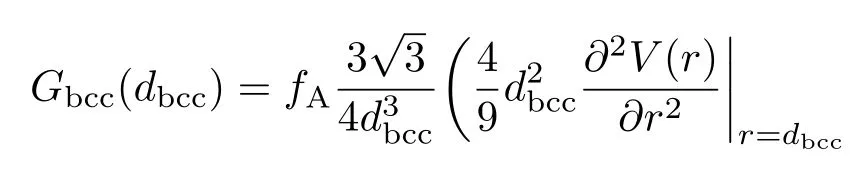
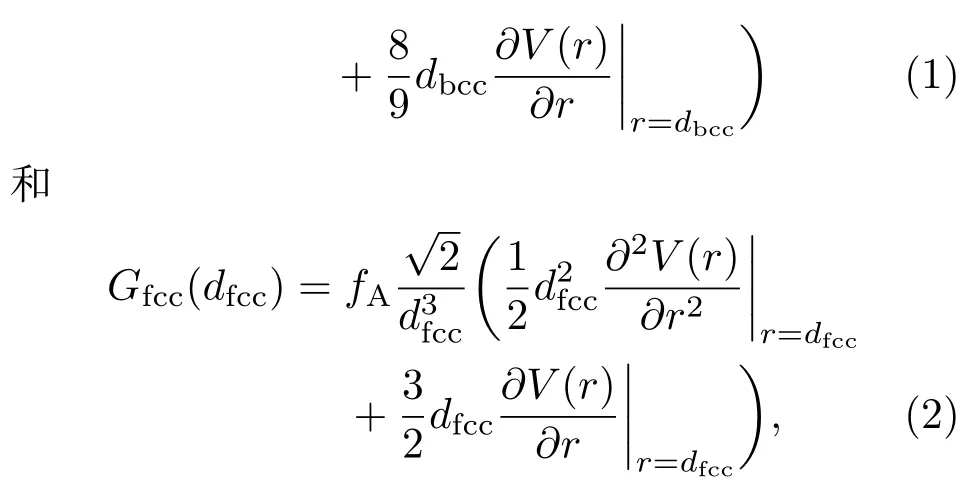
式中dbcc和dfcc分别为bcc和fcc结构的最近邻粒子间距;V(r)表示间距为r的两个粒子间的相互作用势;而fA是一个数值因子,用于表示在平均情况下朝向随机的晶粒具有的不同的边界条件,它的理论极限值分别是应变均匀分布时的fA=0.4和应力均匀分布时的fA=0.6,对于多晶样品,在大多数情况下[19,20]fA=0.5.

然而,已有研究表明,表面带有高电荷的胶体粒子形成的胶体晶体内部存在有孔隙,这些孔隙会降低晶体的剪切模量.本文在拟合弹性有效电荷时,将采用考虑了孔隙影响的修正后的剪切模量-相互作用势关系模型.胶体晶体的孔隙与多孔固体材料的孔隙相类似[21,22].描述多孔固体材料结构特征的最重要的参数是相对密度(ρ/ρ0),其中ρ是考虑孔隙体积时的整体平均密度,ρ0是组成多孔固体的固体材料的密度[23].已有的Gibson-Ashby模型[24]显示多孔固体的杨氏模量大小与相对密度的平方成正比,而与泊松比无关,即剪切模量也与相对密度的平方成正比.于是将此模型类比到同样带有孔隙的胶体晶体中.为此,需要有一个和相对密度(ρ/ρ0)等价的参数.我们这样考虑,当形成的胶体晶体不存在孔隙时,胶体粒子会布满整个胶体样品空间,这时最近邻粒子间距为duni,其值可以由其中的胶体粒子数密度及形成的晶体类型推算得到.当胶体晶体中有孔隙存在时,孔隙会占据一部分空间,实际胶体晶体所占空间就会比整个样品体积小,即相当于胶体晶体本身所占空间被压缩,但总粒子数没有变化,因此最近邻粒子间距将会变小,其值dexp是由实际测量的反射光谱的波峰位置计算得到的.所以有dexp＜duni.如果样品空间被晶体充满,不存在孔隙(当粒子表面电荷低时就是这种情况),dexp和duni两者是相等的.对此问题的描述,可以进一步参考相关的文献[8,25].于是可以得到在胶体晶体中与相对密度(ρ/ρ0)等价的参数为(dexp/duni)3,而孔隙率的大小则为1−(dexp/duni)3.

于是,为了考虑孔隙的影响,可以在剪切模量-相互作用势模型中引入因数(dexp/duni)6,则带有孔隙的胶体晶体整体的剪切模量表达式修正为

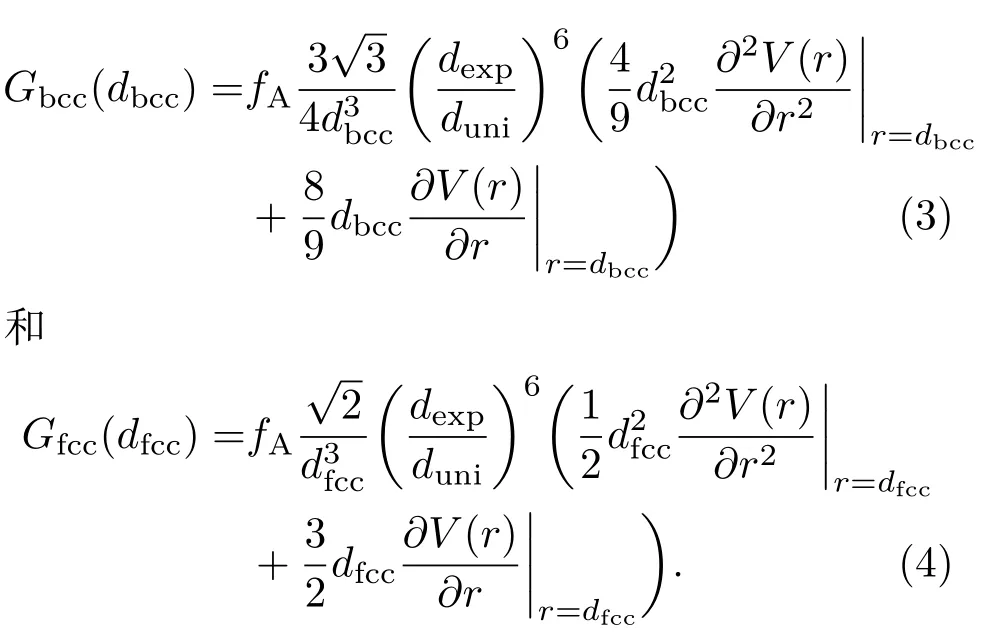
由于上述公式中的dexp/duni以六次方的形式出现,即使dexp/duni十分靠近1时,孔隙的影响也不能忽略.另外,我们将使用Sogam i-Ise(SI)相互作用势代替Yukawa相互作用势,SI作用势中考虑了“以反离子为媒介的引力”,承认了胶体晶体内有孔隙存在[25].Yukawa[26,27]和SI相互作用势[28]的表达式分别如下:

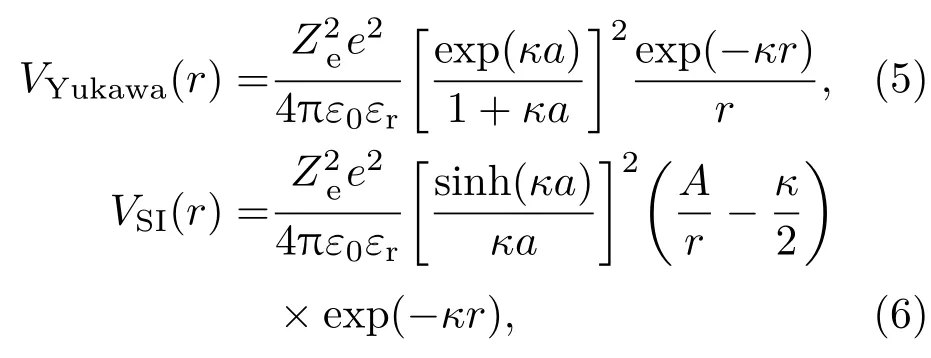
这里Ze是粒子有效电荷数,e是基本电荷,r是粒子间距,a是粒子的半径,A=1+(κa)coth (κa).参数κ是反Debye屏蔽长度,

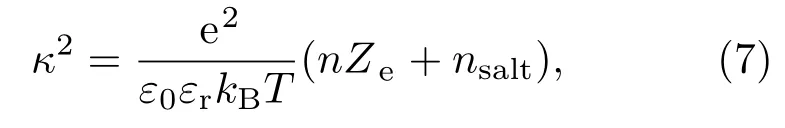
其中n是胶体悬浮液中粒子的数密度,ε0εr是悬浮液的介电常数,kBT是热力学能,而背景电解质盐离子数密度nsalt=2NAc,NA是Avogadro常数,c是其他盐离子的摩尔浓度.

3 材料与实验方法

3.1 聚苯乙烯乳胶粒子与参数测量

本文实验中用到的五种单分散聚苯乙烯乳胶(PSL)粒子是使用乳液聚合法[29]合成而得的,并且通过多次离心和过滤,确保了粒子的单分散性[30,31].粒子的平均直径(2a)和多分散度(PDI)由动态光散射仪(BI-200SM,Brookhaven,USA)测得[2,32],电迁移率µp由激光多普勒测速仪(Zeta-Plus,Brookhaven,USA)测得[33],结果列于表1.

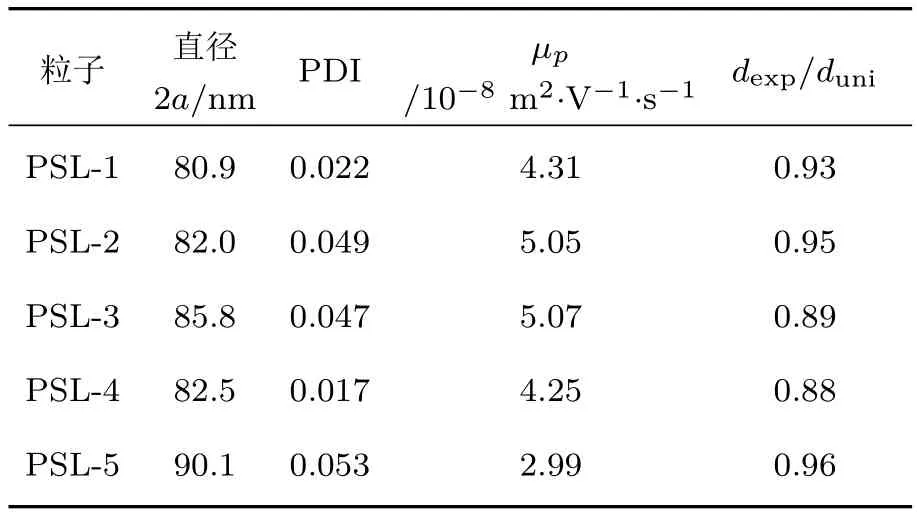
表1 胶体粒子的属性Tab le 1.Param eters of colloidal particles.

由于有孔隙的存在,用反射光谱法测得的胶体晶体最近邻粒子间距dexp往往小于根据粒子数密度计算而得的平均最近邻粒子间距duni.已有研究[8,34]表明,同种粒子形成的胶体晶粒的dexp/duni值一定,并不随着胶体晶体中粒子数密度的改变而改变.本文中所使用的胶体粒子形成的胶体晶体的dexp/duni值见表1.

3.2 平均场归一法

使用平均场归一法得到归一化有效电荷需要知道粒子的固有电荷,因此,我们首先使用电导滴定法测量胶体粒子的固有电荷Z.电导滴定法的实验装置[2]包括储液池、离子交换树脂管、电导电极、电导率测量仪、蠕动泵、恒温水浴和磁力搅拌器.用软管将储液池和离子交换树脂管连接起来,通过蠕动泵驱动可以将储液池中的溶液去离子化.

测量实验在恒温水浴为25℃时进行. 电导滴定时,首先配制含PSL粒子的质量分数在0.01—0.02之间的胶体悬浮液,然后用移液器逐次加入20—40µL的浓度为0.01 mol/L的NaOH标准溶液,用磁力搅拌器混合均匀后记录溶液的电导率σ.溶液的电导率先下降后上升,当稳定上升后停止加入NaOH溶液.

分析电导滴定图1,以PSL-4为例,分别线性拟合电导率σ下降阶段与上升阶段的数据点,两条拟合直线的交点所对应的NaOH溶液的体积为Ve,NaOH,可以认为加入体积为Ve,NaOH的标准NaOH溶液时为中和反应的终点,此时胶体粒子表面电离出的H+离子完全被Na+离子所置换.计算粒子固有电荷的方程为[2,9]

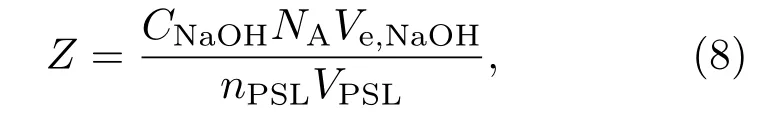
其中,CNaOH为NaOH标准溶液的摩尔浓度,NA为阿伏加德罗常数,Ve,NaOH为中和反应终点时需要的NaOH溶液体积,nPSL为胶体悬浮液中PSL粒子的数密度,VPSL为胶体悬浮液的体积.

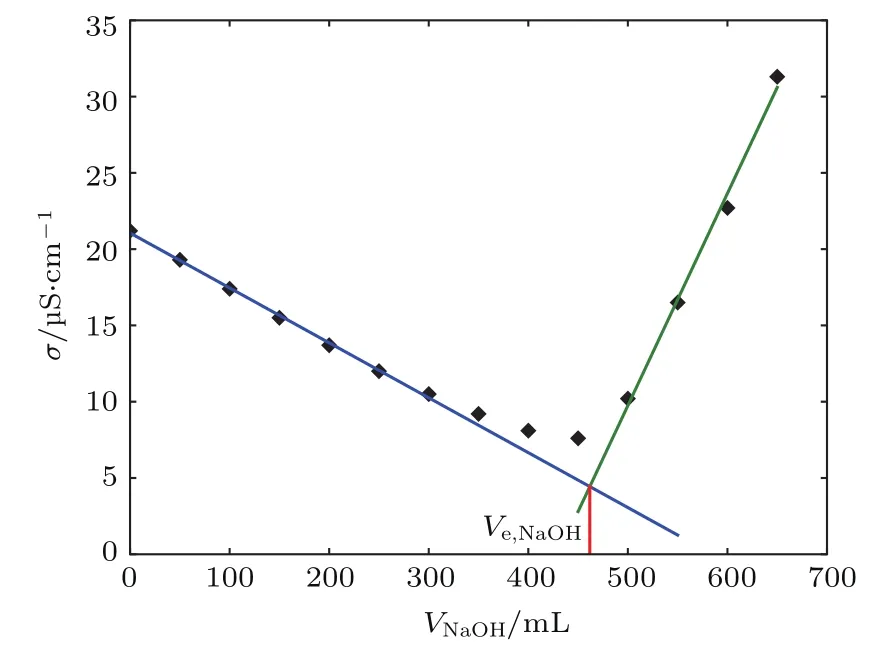
图1 PSL-4胶体粒子的电导滴定曲线Fig.1.Conductom etric titration cu rve of PSL-4.

在测定了固有电荷Z之后,再使用平均场归一法利用数值方法确定粒子的平均场归一电荷.A lexander等[3]在WS球形胞格模型的基础上,把带电粒子之间及与小离子之间的复杂相互作用的多粒子问题简化为单粒子问题.假设每个胞格内的总电荷为零,其大小R=a/η1/3,其中a为胶体粒子半径,η为胶体晶体中胶体粒子的体积分数.由于WS胞格的球对称性,可以通过对PB方程及边界条件[35]

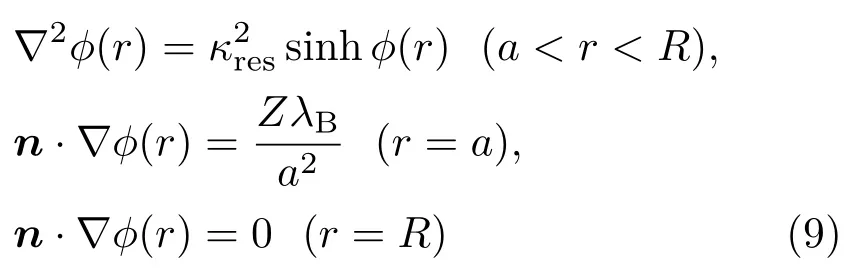
进行数值求解,得到静电平均场势能ϕ(r).这里κres为反屏蔽长度,λB为Bjerrum长度.这样可以得到WS胞格边界处的反屏蔽常数.确定线性化的PB方程

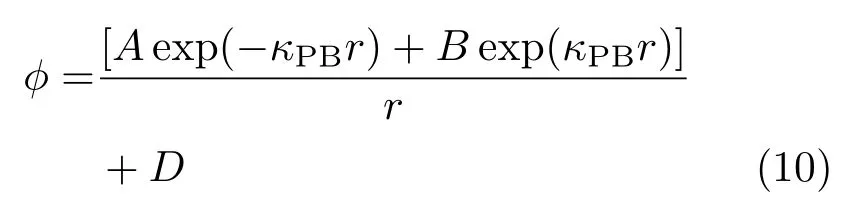
中的系数A,B和D,其边界ϕ值与原PB方程结果在WS边界处直到二阶相等.再根据电荷浓度分布(cs为平均盐浓度)求WS胞格内半径从a到R的总电荷,就可以确定有效电荷的值.

3.3 电导率-数密度法

使用电导率-数密度法可以确定胶体粒子的迁移有效电荷,作为得到有效电荷最简单的方法,其结果可以与弹性有效电荷之间进行参照对比.电导率-数密度法的实验装置与电导滴定法的一样.首先在储液池中加入一定体积的去离子水,然后启动蠕动泵使水通过去离子树脂管进一步去离子.当水的电导率不再变化时,向储液池中逐次加入固定体积的PSL原溶液,每加入一次后,使用磁力搅拌器将溶液混合均匀,同时启动蠕动泵进一步将溶液去离子,待电导率测量仪读数稳定后进行记录.

分析图2所示的电导率-数密度关系,以PSL-4为例,使用电导模型[9,36]

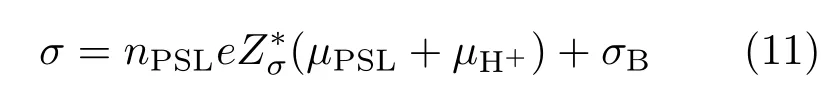
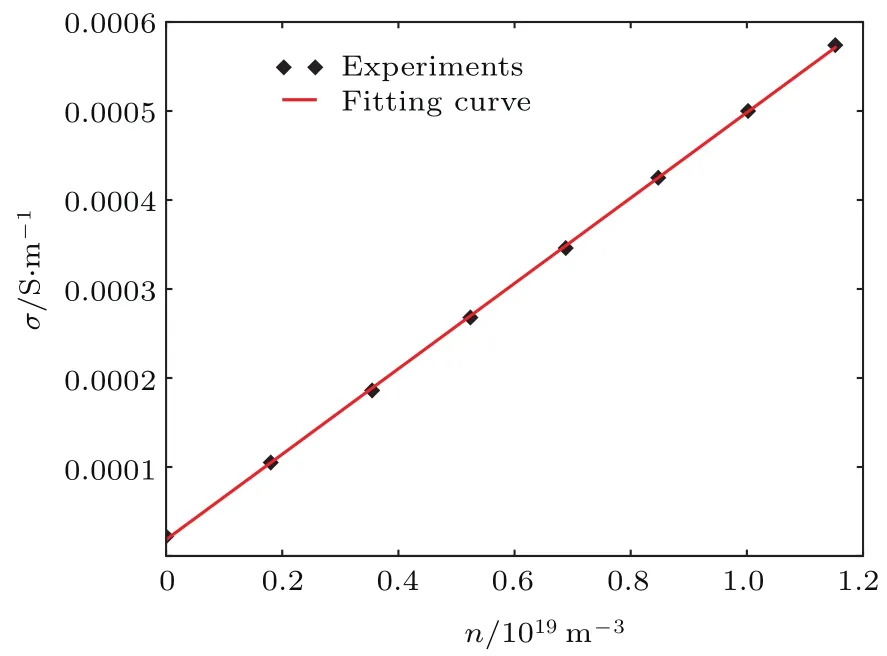
图2 PSL-4粒子的电导率-数密度关系Fig.2.Relationship between electric conductance and num ber density of particles for PSL-4.

3.4 扭转共振法测量剪切模量

粒子的弹性有效电荷需通过测量不同浓度下胶体晶体的剪切模量,再通过理论公式拟合反推得到,因此实验中需要测量剪切模量.我们利用扭转共振法对胶体晶体的剪切模量进行测量,由样品单元和测量单元两部分组成[34].在样品单元中,用软管将样品管、储液池、离子交换树脂管连接起来,并用蠕动泵驱动组成一个去离子循环装置.测量单元包含扭转共振谱仪和反射光谱仪(Avaspec-2048, Avantes,Netherland),反射光谱仪用于测量样品管中胶体晶体的最近邻粒子间距.在扭转共振谱仪工作时,将激光入射到样品管中的胶体晶体上,在满足布拉格衍射条件的位置形成光斑,样品管围绕着中心轴做低幅度的不同频率的旋转振动时,带动光斑发生周期性的振动,位敏传感器将光斑运动时产生的驻波信号传入锁相放大器中.可以观测到的胶体晶体剪切模量为G时的共振频率大小为[14,18,37]

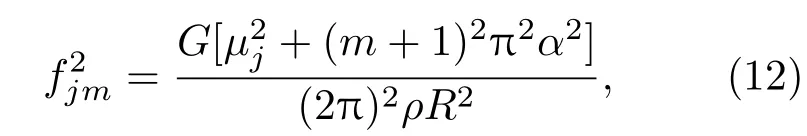
这里j和m是共振阶数(the indices of the order of the resonances),α是样品管内径R与胶体晶体填充高度H的比值,ρ是胶体晶体的质量密度,µj为一阶贝塞尔函数J1的零点.

4 结果与讨论

本文先使用扭转共振法测得不同粒子数密度时胶体晶体的剪切模量值,再分别使用修正前和修正后的剪切模量-相互作用势关系模型来拟合有效电荷.拟合过程中,将有效电荷Ze和盐浓度nsalt作为自由拟合参数.拟合曲线以粒子PSL-4为例,如图3所示,五种不同PSL粒子的弹性有效电荷的拟合结果见表2,其中是使用修正前的剪切模量-相互作用势关系模型得到的弹性有效电荷值,是使用修正之后的剪切模量-相互作用势关系模型得到的弹性有效电荷值,是仍然使用Yukawa作用势但使用修正之后的模型表达式拟合得到表面有效电荷.若以平均场归一法计算得到的平均场归一电荷作为参照值,可以从表中看出,使用修正模型得到的弹性有效电荷值比使用修正前模型得到的弹性有效电荷值大很多,且与参照值平均场归一电荷更为接近,误差在25%以内,与文献[12]中由没有孔隙存在的胶体晶体中得出的弹性有效电荷的对比情况一致.另外,我们还发现的值介于与之间,且与的差异较小,可以推断使用修正的剪切模量-相互作用势关系模型带来的影响效果远大于用SI作用势代替Yukawa作用势的影响.

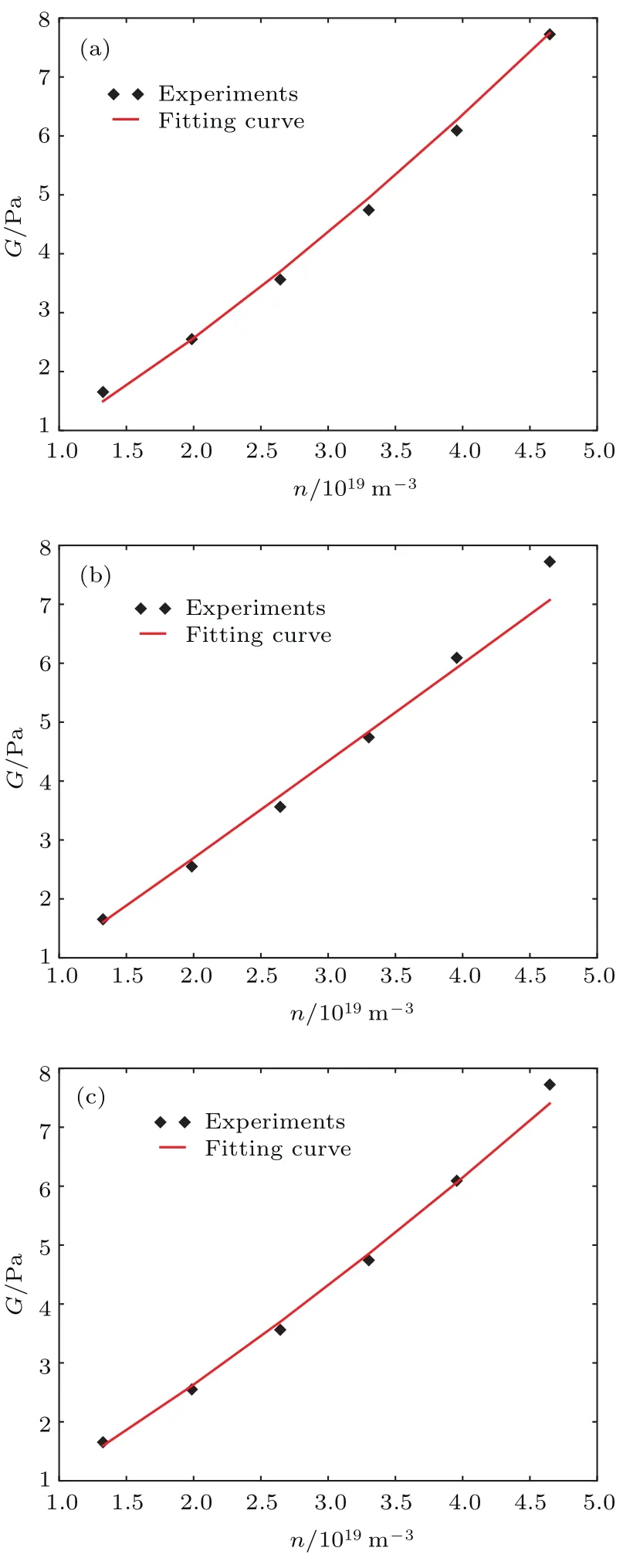
图3 使用修正前及修正后的剪切模量-相互作用势模型的参数拟合 (a)PSL-4,没有考虑孔隙;(b)PSL-4,考虑了孔隙,并使用了SI作用势;(c)PSL-4,考虑了孔隙但使用了Yukawa作用势Fig.3. Param eter fi tting using shear m odu lusinteraction potential before and after m od ifi cation: (a)PSL-4,not considered voids;(b)PSL-4,considered voids and using SI potential;(c)PSL-4,considered voids and using Yukawa potential.

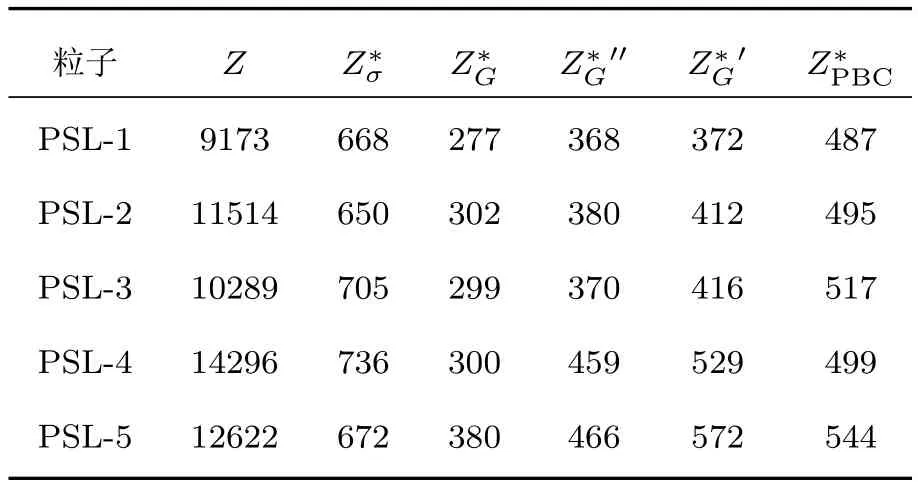
表2 胶体粒子的固有电荷和有效电荷Tab le 2.Intrinsic and eff ective charge of colloidal particles.

5 结 论

本文针对五种带电粒子形成的存在孔隙的胶体晶体体系,利用扭转共振法测量了其不同体积分数时的剪切模量,并通过拟合反推得到了粒子的弹性有效电荷,并将测量结果与迁移有效电荷及平均场归一化有效电荷进行了对比.在反推过程中,我们改进了已有的理论公式,考虑了胶体晶体中孔隙的影响,在拟合使用的关系模型中引入了孔隙影响系数,并使用了SI相互作用势来代替Yukawa作用势.通过实验结果的对比发现,使用修正的关系模型得到的弹性有效电荷的值与平均场归一化有效电荷的结果也更为接近,而采用原有的理论模型得到的值则与平均场归一化电荷差别很大,从而也有效验证了理论改进的合理性,在一定程度上解释了以前不能用迁移有效电荷或平均场归一化有效电荷估算剪切弹性模量的原因.此外,比较了不同形式有效电荷之间的大小关系,其结果可以为人们进一步了解和使用胶体粒子的有效电荷提供参考.

[1]Denton A R 2010 J.Phys.-Condens.M atter 22 364108

[2]Zhou H W,M i L,Liu L X,Xu SH,Sun ZW 2013 Acta Phys.Sin.62 134704(in Chinese)[周宏伟,米利,刘丽霞,徐升华,孙祉伟2013物理学报62 134704]

[3]A lexander S,Chaikin P M,G rant P,M orales G J,Pincus P,Hone D 1984 J.Chem.Phys.80 5776

[4]G rosse C,Shilov V N 2000 J.Colloid In terf.Sci.225 340

[5]Palberg T,Schwein furth H,Köller T,Müller H,Schöpe H J,Reinmüller A 2013 Eur.Phys.J.-Spec.Top.222 2835

[6]Ito K,Sum aru K,Ise N 1992 Phys.Rev.B 46 3105

[7]Ouyang W,Zhou H,Xu S,Sun Z 2014 Colloid.Surface A 441 598

[8]Zhou H,Xu S,Ouyang W,Sun Z,Liu L 2013 J.Chem. Phys.139 064904

[9]Gong Y K,Nakashim a K,Xu R 2001 Langm uir 17 2889

[10]Belloni L 1998 Colloid.Surface A 140 227

[11]W ette P,Schöpe H J,Palberg T 2002 J.Chem.Phys. 116 10981

[12]Shap ran L,M edebach M,W ette P,Palberg T,Schöpe H J,Horbach J,K reer T,ChatterjiA 2005Colloid.Surface A 270–271 220

[13]W ette P,Schöpe H J,Palberg T 2003 Colloid.Surface A 222 311

[14]Dubois-V iolette E,Pieranski P,Rothen F,Strzelecki L 1980 J.Phys.France 41 369

[15]Joanny J F 1979 J.Colloid Interf.Sci.71 622

[16]Yoshida H,Ito K,Ise N 1991 Phys.Rev.B 44 435

[17]Zhou H,Xu S,Sun Z,Du X,Liu L 2011 Langm uir 27 7439

[18]Zhou H,Xu S,Sun Z,Zhu R 2015 J.Chem.Phys.143 144903

[19]Hashin Z,Shtrikm an 1962 J.M ech.Phys.So lids 10 343

[20]Zeller R,Dederichs P 1973 Phys.Status Solidi B 55 831

[21]Anderson V J,Terentjev E M,M eeker S P 2001 Eur. Phys.J.E 4 11

[22]Anderson V J,Terentjev E M 2001 Eur.Phys.J.E 4 21

[23]Ashby M F,M edalist R F M 1983 M etall.Trans.A 14 1755

[24]Nieh T,K inney J,Wadsworth J,Ladd A 1998 Scripta M ater.38 1487

[25]Ise N,Konishi T,Tata B V R 1999 Langm uir 15 4176

[26]Stevens M J,Falk M L,Robbins M O 1996 J.Chem. Phys.104 5209

[27]Tata B V R,Ise N 1996 Phys.Rev.B 54 6050

[28]Sogam i I,Ise N 1984 J.Chem.Phys.81 6320

[29]W ang Q,Fu S,Yu T 1994 Prog.Polym.Sci.19 703

[30]Du X,Xu S H,Sun Z W,Liu L 2012 Chin.J.Chem. Phys.25 318

[31]Shou ldice G T D,Vandezande G A,Rudin A 1994 Eur. Po lym.J.30 179

[32]Goldburg W I 1999 Am.J.Phys.67 1152

[33]X iong B,Palland re A,le Potier I,Audebert P,Fattal E, Tsapis N,Barratt G,Taverna M 2012 Anal.M ethods 4 183

[34]Q in Y M,Zhou H W,Xu S H,Sun ZW 2015 Chem.J. Chinese Univ.36 310(in Chinese)[秦艳铭,周宏伟,徐升华,孙祉伟2015高等学校化学学报36 310]

[35]Trizac E,Bocquet L,Aubouy M,von G rünberg H H 2003 Langm uir 19 4027

[36]Hessinger D,Evers M,Palberg T 2000 Phys.Rev.E 61 5493

[37]Joanicot M,Jorand M,Pieranski P,Rothen F 1984 J. Phys.France 45 1413

PACS:61.46.Bc,64.70.pv,82.70.Dd,47.57.–sDOI:10.7498/aps.66.066102

Theoretical im p rovem en t on the determ ination of eff ective elasticity charges for charged colloidal particles∗

Wang Lin-Wei1)2)†Xu Sheng-Hua2)3)‡Zhou Hong-Wei2)Sun Zhi-Wei2)Ouyang Wen-Ze2)Xu Feng1)

1)(School of Civil Engineering,Beijing Jiaotong University,Beijing 100044,China)
2)(Key Laboratory ofM icrogravity,Institu te ofM echanics,Chinese Academ y of Sciences,Beijing 100190,China)
3)(School of Engineering Science,University of Chinese Academ y of Sciences,Beijing 100049,China)
(Received 22 Novem ber 2016;revised m anuscrip t received 17 Decem ber 2016)

According to the existing shear m odulus-pair potential relationship m odel for colloidal crystal com prised of highly charged colloidal particles,the calculated shear m oduli of colloidal crystals are much larger than the m easured values by the torsional resonance spectroscopy(TRS).M oreover,by using the relationship model,the eff ective surface charge of colloidal particles,obtained by fi tting values of shearm odulim easured by TRS(eff ective elasticity charge),is sm aller than that obtained through the experimentalmethod of conductivity-number density relationship(eff ectively transported charge).So far there has been no practical exp lanation to this discrepancy.Our analysis shows that this discrepancy is because the existing relationship m odel is for the perfect crystals and does not include the defects such as voids which can resu lt in the decrease ofmechanical p roperties ofmaterials.The existing shear modulus-pair potentialmodel w ill be im proved by introducing the eff ect of voids,which is inspired from the Gibson-Ashby m odel in the study of cellular solid.The Yukawa potential,which considers Cou lomb repulsions between colloidal particles and is usually used in themodel exp ressions,w ill be substituted by Sogam i-Ise potential,which considers a long-range attraction in addition to that Coulomb repulsions and accep ts the existence of voids inside the colloidal crystals.For five diff erent kinds of high ly charged colloidal particles,the shear m odu li w ith diff erent volume fractions are m easured by TRS.Then the fi tted eff ective surface charges using the original and im p roved model respectively are com pared w ith each other.It can be concluded that the eff ective elastic charge obtained by the im proved m odel ism ore suitable and much closer to the renorm alized charge obtained from A lexander’smethod.It is also clear that neither the eff ectively transported charge nor the A lexander’s renormalized charge can be used to evaluate the shearmoduliof colloidal crystalsw ith voids inside. These resu lts can also let us further understand and use the eff ective surface charge in the colloid studies.

eff ective charge,shearmodulus,voids,colloidal crystal

10.7498/aps.66.066102

∗国家自然科学基金(批准号:11302226,11572322,11672295)资助的课题.

†通信作者.E-m ail:wanglinwei@outlook.com

‡通信作者.E-m ail:xush@im ech.ac.cn

*Pro ject supported by the National Natural Science Foundation of China(G rant Nos.11302226,11572322,11672295).

†Corresponding author.E-m ail:wanglinwei@outlook.com

‡Corresponding au thor.E-m ail:xush@im ech.ac.cn