基于变温霍尔效应方法的一类n-GaN位错密度的测量∗

何菊生张萌 潘华清 邹继军 齐维靖 李平

1)(南昌大学科学技术学院,南昌 330029)

2)(南昌大学材料科学与工程学院,南昌 330031)

3)(上饶职业技术学院机械工程系,上饶 334100)

4)(核技术应用教育部工程研究中心(东华理工大学),南昌 330013)

5)(南昌大学现代教育技术中心,南昌 330031)

(2016年10月23日收到;2016年12月8日收到修改稿)

基于变温霍尔效应方法的一类n-GaN位错密度的测量∗

何菊生1)†张萌2)潘华清3)邹继军4)齐维靖2)李平5)

1)(南昌大学科学技术学院,南昌 330029)

2)(南昌大学材料科学与工程学院,南昌 330031)

3)(上饶职业技术学院机械工程系,上饶 334100)

4)(核技术应用教育部工程研究中心(东华理工大学),南昌 330013)

5)(南昌大学现代教育技术中心,南昌 330031)

(2016年10月23日收到;2016年12月8日收到修改稿)

结合莫特相变及类氢模型,采用浅施主能量弛豫方法,计算了一类常见n-GaN光电子材料的载流子迁移率,给出了精确测定其刃、螺位错密度的电学方法.研究表明,对于莫特相变材料(载流子浓度超过1018cm−3),以位错密度Ndis、刃螺位错密度比β、刃位错周围浅施主电离能εD1、螺位错周围浅施主电离能εD2为拟合参数的载流子迁移率模型与实验曲线高度符合,拟合所得刃、螺位错密度与X射线衍射法或化学腐蚀方法的测试结果也基本一致.实验结果表明,莫特相变材料虽然载流子浓度高、霍尔迁移率低,但其位错密度却并不一定高过载流子浓度低、霍尔迁移率高的材料,应变也无明显差异,因此,莫特相变与刃、螺位错密度及两类位置最浅的施主均无关系,可能是位置较深的施主或其他缺陷所致,需要比一般杂质带高得多的载流子浓度.该方法适合霍尔迁移率在0 K附近不为零,霍尔迁移率曲线峰位300 K左右及以上的各种生长工艺、各种厚度、各种质量层次的薄膜材料,能够对迁移率曲线高度拟合,迅速给出莫特相变材料的相关精确参数.

氮化镓,霍尔迁移率,位错密度,莫特相变

1 引 言

氮化镓(GaN)具有优异的光电性能,其位错密度的测试是其质量分析中的一项重要内容[1,2],相关研究长期以来一直是半导体领域的学术热点.然而,目前两类主要的测试方法X射线衍射(XRD)法和化学腐蚀(EPD)法都有很大的不确定性,有时甚至只有数量级意义.位错具有显著的光学、化学特性,其电学特性也极为显著,表现为van der Pauw变温霍尔效应测试具有极高的灵敏度,借助于计算机自动测试和电学统计平均方法,可以比XRD和EPD更精确地测定n-GaN的刃、螺位错密度[3],非常适合高迁移率材料和器件.可是对发光二极管、激光二极管等一些光电子器件而言,室温霍尔迁移率偏低,在0 K附近不为零,且霍尔迁移率曲线峰位在300 K左右及以上,并不符合我们在文献[3]中提出的“霍尔迁移率曲线峰位在200 K左右及以下”(0 K时霍尔迁移率为0)的条件.为此,本文基于纤锌矿n-GaN的莫特相变(M ott transition)分析,对我们在文献[3]中所描述的材料之外的样品进行XRD和van der Pauw变温霍尔效应测试,得到了一类常见材料的位错密度精确测定方法.

利用电学方法(霍尔迁移率曲线拟合)来测试位错密度,比光学(XRD)和化学(EPD)方法在精确性方面更具优势.这里有两方面的原因:一是虽然n-GaN材料内杂质种类众多且极为复杂,但只有聚集于刃、螺位错线周围呈六棱柱形分布的两类点缺陷能级位置最浅,最接近费米能级,霍尔迁移率基本上只受它们影响,且随着温度的变化,位错结构表现出极高的稳定性,使得霍尔迁移率与位错在各种温度下都如影相随,最适合直接反映位错密度水平;二是虽然n-GaN材料内热、光、电三者能量关系极为复杂,但是霍尔迁移率本质上只是浅能级电离能量活跃度的反映,干扰因素很少,且可以用各类宏观统计量来精确描述.

半导体发生莫特相变后电子载流子的能量与金属自由电子非常类似,几乎不随温度变化,与相变前对温度很敏感(电子动能为Ek=3kBT/2,其中kB为玻尔兹曼常数,T为温度)有很大不同.目前学术界对GaN材料莫特相变只有少量的实验研究,常常是变温霍尔效应测试的对比研究[4,5].本文基于莫特相变材料的电离特征,理论上给出了霍尔迁移率的一般形式,并得到实验验证,可用于位错密度的精确测定.

2 实验与原理

2.1 类氢模型与莫特相变

n-GaN材料虽然浅施主杂质种类众多且极为复杂,但其平均效果,可以用类氢模型来描述.杂质中心电子的半径为a=κ0aBm0/m=2.5×10−9m,其中静态相对介电常数κ0=10.4,氢原子玻尔半径aB=0.53×10−10m,电子有效质量m=0.22m0,当电子波函数半径约为4a,即载流子浓度n≈1/(4a)3≈1018cm−3时,电导将向金属性过渡,这就是莫特相变.这时,处于高掺杂状态的杂质原子外层电子波函数明显交叠,孤立的杂质能级扩展为能带,最多只有一个电子的杂质带能级实际可接受两个电子,也就是说,杂质带不到半满状态,杂质电子既可通过隧穿在带内实现电导,也可通过电离实现电导.

莫特相变状态下电离最明显的一个特征是:杂质隧穿电子能量稳定度极高,使得浅施主杂质吸收能量电离的过程变得很缓慢,热电离和碰撞电离似乎不存在,浅施主杂质几乎都是依靠温度涨落(自发跃迁)才能电离,导致迁移率明显偏低,出现低温下迁移率不低(可超过100 cm2/(V·s))、高温下迁移率不高(最高300 cm2/(V·s)左右)的现象.这种扁平状迁移率曲线与莫特相变前(载流子浓度小于1018cm−3)完全不同:位置较浅的刃位错线周围一个浅施主可以瞬间吸收一个光学声子热电离(设电离能为εD1),位置较深的螺位错线周围一个浅施主也能受到电子碰撞瞬间电离(设电离能为εD2),导致低温下迁移率为零,室温下可超过900 cm2/(V·s),电离能量活跃度随温度急剧变化.

莫特相变状态下电离的另一个明显特征是:类氢模型下,能量稳定度极高的隧穿电子,在导带底附近形成了一个鲜明的杂质电子海“海面”,电离就发生在“海面”电子与上方近距离的导带底之间,考虑隧穿电子对原子核引力的屏蔽作用,“海面”就在类氢模型的某一能级上.取导带底为能级零点,由能级En=−m E0/(m0κ20n2)=(−27.7/n2)meV,其中氢原子基态能量E0=−13.6 eV,得E1至E6分别位于导带底下27.7,6.92,3.07,1.73,1.11, 0.77 meV处,由于海森伯不确定关系(存在零点振动能),靠近导带底的类氢能级上杂质电子能轻易进入导带,或者说这些较高能级实际不存在.Osinnykh等[6]用光致发光方法观察到导带底约6,2.5, 1 meV三个能级,并指出0.8 meV(10 K时的原子振动动能为kBT)以上的能级难以观察到,据此我们可以认为导带底E5(=1.11 meV)为类氢模型的最高能级,为杂质带电子“海面”.

2.2 浅施主能量弛豫计算

每条位错线周围都有6条浅施主杂质线,由此用位错密度Ndis和c轴晶格常数得到单个浅施主杂质占据的体积V为[3]

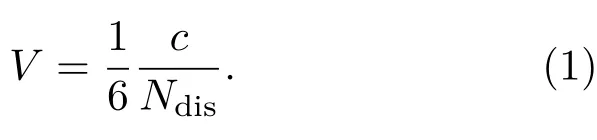
在晶格能量弛豫过程中,单位时间里从单施主上释放的总能量,采用类氢施主电离能εD(=m e4/[2(4πκ0ε0ħ)2])、 光学声子频率ωLO表示为

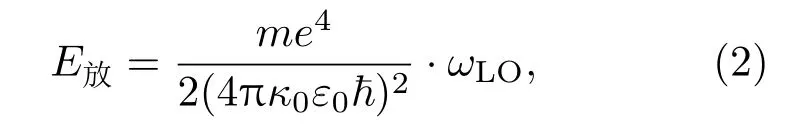
其中e,m分别为电子电量和有效质量;κ0为静态相对介电常数;ε0为真空介电常数;ħ为普朗克常数.而单位时间里单施主杂质吸收的能量由单位时间内受到一次碰撞的概率1/τ(τ为晶格能量弛豫时间)、光学声子能量ħωLO、单施主体积V、能量状态密度4π(2mħωLO)3/2/[8(2πħ)3]及单施主能量宏观吸收率k决定[3],

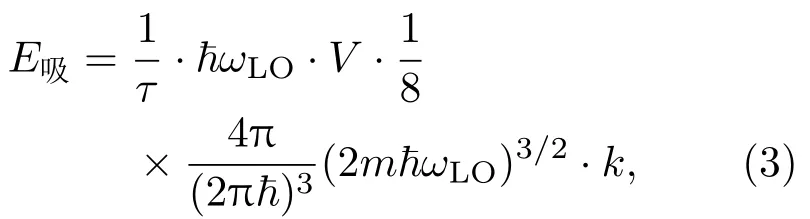
其中k由光学声子能量ħωLO(=91.2 meV)、吸收一个光学声子引起的电子电离数ζ、莫特相变后类氢施主电离能E5(={m e4/[2(4πκ0ε0ħ)2]}/25)决定,

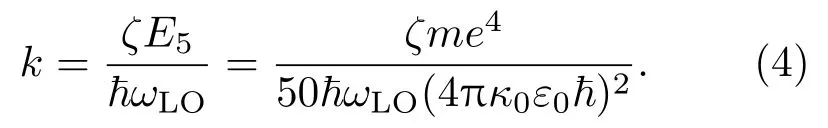
如前所述,实际情况是有两类杂质原子电离.在热运动中,电子获得能量ΔE的概率为e−ΔE/(kBT).对于位置较深的螺位错线周围浅施主而言,电离极其微弱,基本不受导带底电子状态的影响,电离概率用电离能εD2表示为e−εD2/(kBT),而位置较浅的刃位错线周围浅施主,电离非常强烈,ΔE由与导带底电子占有状态有关的能量宏观吸收率k′、杂质原子热振动动能kBT、两类浅施主数目之比β三者决定,

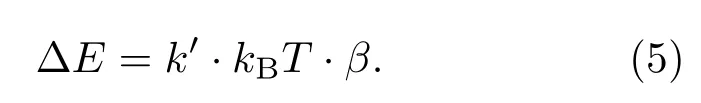
为求k′,用fC=1/[1+exp(EC−EF)/(kBT)], fD1=1/[1+1/gD·exp(ED1−EF)/(kBT)]分别表示导带底和杂质能级上的电子占有率,其中简并因子gD=2,而平均非占有率分别为(1−fC), (1−fD1).在热平衡情况下,向上跃迁的电子数和向下跃迁的电子数相同,有

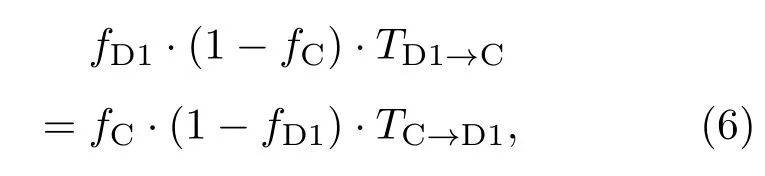
其中TD1→C,TC→D1分别是杂质能级ED1至导带底、导带底至杂质能级ED1的电子宏观跃迁率,由此得ED1能级上电子一次循环的能量宏观吸收率k′:

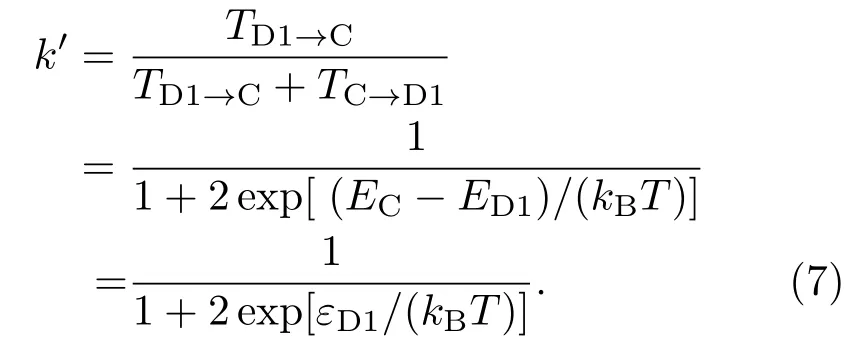
于是吸收一个光学声子引起的电子电离数ζ为

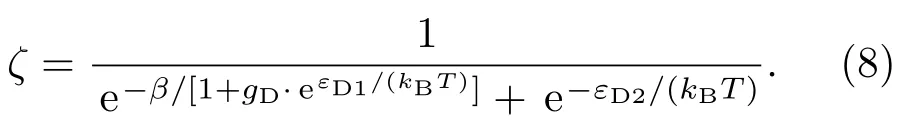
由方程(1),(2),(3),(4)和(8)得载流子迁移率

如位错密度、迁移率分别以cm−2,cm2/(V·s)为单位,则µ可表示为

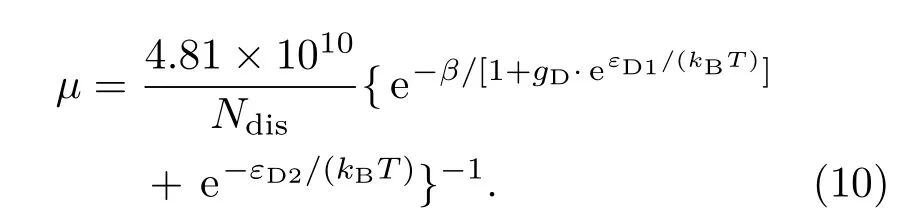
以Ndis,β,εD1,εD2为参数用(10)式对霍尔迁移率曲线µH-T进行拟合,即可得到螺位错、刃位错密度,

2.3 实 验

采用荷兰帕纳科公司X’Pert Pro MPD型X射线衍射仪测试了17#,32#两实验样品的多个晶面的半高全宽(FWHM),用Srikant方法[7]拟合得到面内扭转角(tw ist)和面外倾斜角(tilt),用N edge= β2twist/(4.35b2e)和N screw= β2tilt/(4.35b2s)换算得刃、螺位错密度,其中be=0.3189 nm, bs=0.5185 nm.拟合效果如图1所示,拟合参数见表1,换算结果见表2.

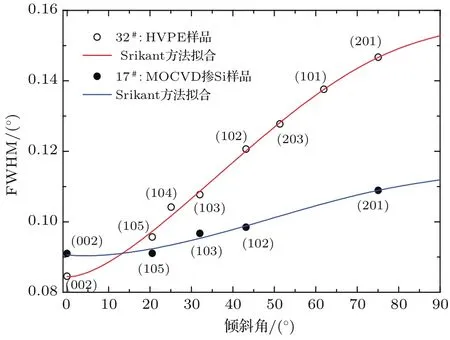
图1 (网刊彩色)17#,32#样品各晶面FW HM与倾斜角的关系Fig.1.(color on line)W id th ofω-scans as a function of inclination angleψfor sam p le 17#grown by MOCVD and 32#grown by HVPE.The sym bols are experim ental data and the lines are fi tting cu rves by using Srikant m odel.

表1 17#,32#样品Srikant方法拟合参数Tab le 1.Param eters of sam p le17#,32#fi tted by Srikant m ethod.

van der Pauw变温霍尔效应测试采用ECOPIA公司的HMS-5000/HMS-5500全自动变温霍尔效应测试仪.测试电流为1 m A,磁场为5.5 kG,温控精度0.5 K,样品尺寸10mm×10mm,铟作电极,测试范围为80—520 K,测试结果如图2所示.

3 结果与讨论

图2表明,实验曲线和(10)式符合得很好,根据拟合值Ndis和β,由(11a)和(11b)式得到的刃、螺位错密度与XRD方法结果也有很好的一致性.我们还对文献[8]的霍尔迁移率曲线进行了拟合,不仅曲线拟合较好,而且位错密度与EPD法结果也基本一致,如表2所列.

图2 (网刊彩色)本文方法对17#,32#样品霍尔迁移率的拟合Fig.2.(color on line)Experim ental(points)and m odel (solid lines)m obility for sam p le 17#and 32#.The latter is determ ined by a least-square fi t to our shallow donor energy relaxation calcu lation m ethod using Eq.(10).

表2 XRD或EPD实验结果与迁移率拟合结果比较Tab le 2.The d islocation density com parison from the experim ental values and ou r m odel values through fi ttingµHvs T data(unit:108cm−2).

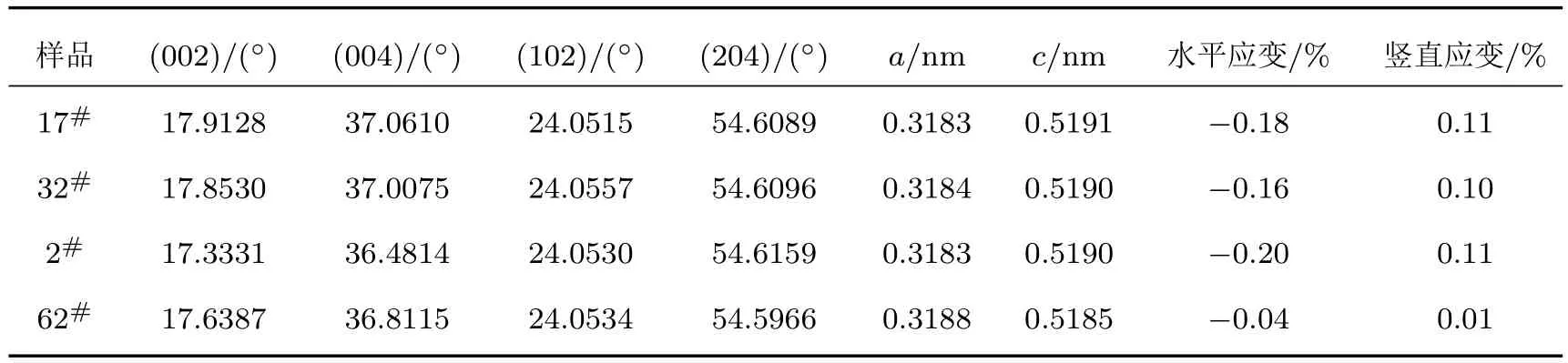
表3 莫特相变材料(17#,32#)与非莫特相变材料(2#,62#)应变比较Tab le 3.The strain com parison between the M ott transition m aterials(17#,32#)and them aterialw ithout M ott transition(2#,62#).

值得注意的是,由于莫特相变,材料载流子浓度高于1018cm−3,室温迁移率一般低于300 cm−2/(V·s)、可是其位错密度却与那些低载流子浓度(低于1018cm−3)、高霍尔迁移率材料相当,甚至可能更低,可见,仅凭室温载流子浓度和迁移率两个参数不能估算位错密度水平.那么,是否我们所测试的材料刚好内部应力很大,尚未通过进一步产生位错来释放应力?为此,我们对17#,32#样品进行了ω-2θ扫描,分别拟合出了(002),(004), (102),(204)四个晶面的衍射峰位,如表3所列.采用文献[9]的方法,消除仪器零点误差后,得到了晶格常数的精确值,由此得到准确的水平和竖直应变.作为比较,同样测试了两个我们在文献[3]报道的未莫特相变的样品2#,62#(其中62#是体材料),结果表明,四个样品应变都很低,不存在进一步释放应力的可能.因此,我们认为,在目前成熟的制备工艺里,莫特相变材料(载流子大于1018cm−3)与相对的非莫特相变材料都是晶格完美的低应变材料.

由于仪器最低测试温度所限(液氮),这里我们选择了80—520 K进行测试.实际上,如果仪器最低测试温度能低到10 K左右,选择0—300 K范围测试,(10)式将会有极高的精确度.因为(10)式表明,温度趋于零时,霍尔迁移率完全由位错密度确定,霍尔迁移率高的材料位错密度低,霍尔迁移率低的材料位错密度高,可极大地排除各种干扰因素.为此,我们对文献[4]的测量结果进行了拟合,如图3所示.M avroidis等[4]对样品No.1进行了三次刻蚀,厚度从1.18µm先后减为0.94,0.82, 0.56µm,且先后进行了四次van der Pauw变温霍尔效应测试,并采用公式

计算了刻蚀掉的3层的霍尔浓度和霍尔迁移率nr, µr,其中nsb,µb表示刻蚀前测到的二维载流子浓度和霍尔迁移率;nsa,µa表示刻蚀后测到的二维载流子浓度和霍尔迁移率;t表示样品厚度.拟合结果表明,每组实验数据符合得都很好,并能给出精确拟合值,如表4所列.其中刃、螺位错密度的误差由下式算得:

式中误差ΔNdis,Δβ由曲线拟合给出.

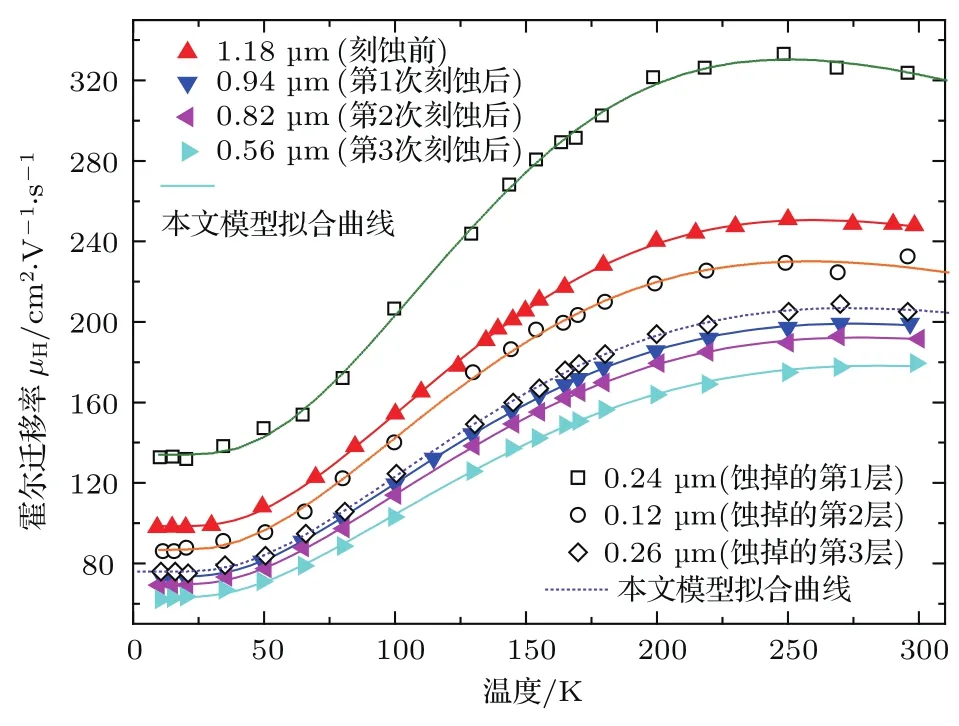
图3 (网刊彩色)(10)式对文献[4]经过连续3次刻蚀的样品霍尔测试结果的拟合Fig.3.(color on line)Experim entalµHvs T data (points)of sam p le No.1 from Ref.[4]fi tted using Eq.(10).▲,as grow n,1.18µm thick;▼,after fi rst etch to 0.94µm;◀,after second etch to 0.82µm;▶, after third etch to 0.56µm.

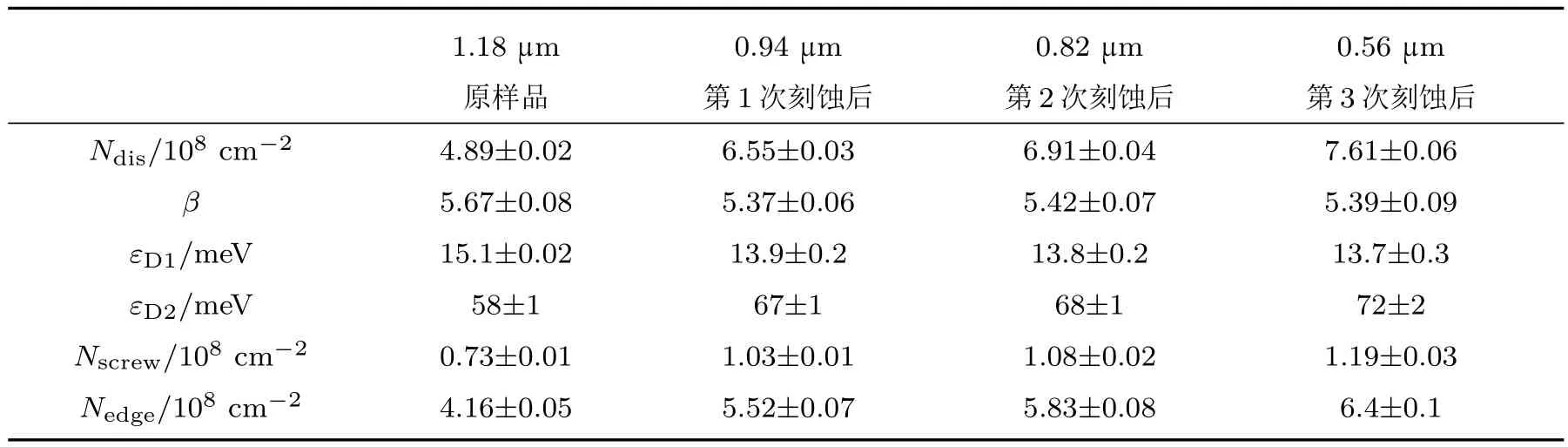
表4 文献[4]No.1样品(图3)的拟合参数,刃、螺位错密度及其误差Tab le 4.Fitted param eters of sam p le No.1 from Ref.[4](Fig.3.)and ou r calcu lation values based on error theory.

由表4可知,随着薄膜增厚,不断有位错终止于膜内晶界处,位错密度逐渐降低,但β基本不变,表明刃、螺位错终止于晶界处的速度基本一致.刃、螺位错密度的急剧降低,意味着周围浅施主能级ED1,ED2上点缺陷数目的急剧减少,而文献[4]报道样品的载流子浓度一直维持在1018cm−3以上并无明显变化,这表明,莫特相变另有原因.事实上,我们在用Rode迭代法[10,11]计算2#(室温载流子浓度为6.9×1017cm−3,位错密度为1.4×109cm−2)等一些载流子浓度1017cm−3量级的样品时发现载流子浓度会远超电离施主浓度,电平衡方程已不成立,薄膜内已出现杂质带.而本文表4中样品的位错密度更低,浅施主ED1,ED2浓度更低,反而出现莫特相变,这说明莫特相变不是位置最浅的两类施主引起的,而是位置较深的施主或其他缺陷所致,需要比一般杂质带高得多的载流子浓度.

另外,将表4中两类杂质的电离能与其浓度关系(ND1=6Nedge/c,ND2=6Nscrew/c)绘成图4,可直观地看出形成杂质带的杂质浓度大小.形成杂质带时,随着杂质浓度的增加,杂质电子会发生轨道交叠,受杂质中心的束缚减弱,这样杂质电离能随杂质浓度的增加而降低,即浅施主电离能εD与浅施主浓度ND的关系为,其中ED0由杂质种类决定,n-GaN的屏蔽因子α大约为2.7×10−5meV·cm[10,11].图4表明,εD1明显小于εD2,那是因为εD1对应的浅施主浓度ND1已处于杂质带,这从杂质电离能随杂质浓度的增加而降低这一特征可清楚看出;而εD2则相反,不但没有因为轨道交叠而产生易电离的弱束缚区,而且一旦电离就面临来自周围同样杂质中心的束缚,周围杂质中心越多,束缚也越多,要想摆脱束缚就越困难,因此εD2随杂质浓度ND2的增加而增大.

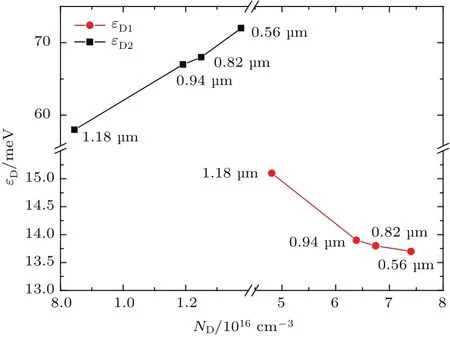
图4 表4中浅施主电离能εD1,εD2随浅施主浓度ND1, ND2的变化Fig.4.Ionization energy of shallow donor versus its concentration from Tab le 4.

4 结 论

本文针对光学或化学方法难以精确测定纤锌矿n-GaN材料位错密度问题,提出了对于一类常见光电子材料(载流子浓度在1018cm−3以上),可以通过拟合霍尔迁移率曲线,由拟合参数来精确确定刃、螺位错密度的电学测定方法.该方法以莫特相变和类氢模型为基础,围绕刃、螺周围浅施主杂质的电离能量活跃度(能量弛豫)进行了相关统计宏观量的计算.研究表明,从霍尔迁移率曲线到刃、螺位错密度,理论和实验都有很好的一致性.该方法适用于0 K附近霍尔迁移率不为零,曲线峰位在300 K左右及以上的各种生长工艺、各种厚度、各种掺杂、各种质量层次的纤锌矿n-GaN薄膜材料.

感谢南昌大学国家硅基LED工程技术研究中心在实验测试方面提供的大力支持.

[1]Zhang Y,X ie Z L,W ang J,Tao T,Zhang R,Liu B, Chen P,Han P,Shi Y,Zheng Y D 2013 Acta Phys.Sin. 62 056101(in Chinese)[张韵,谢自力,王健,陶涛,张荣,刘斌,陈鹏,韩平,施毅,郑有炓2013物理学报62 056101]

[2]Q iW J,Zhang M,Pan S,W ang X L,Zhang J L,Jiang F Y 2016 Acta Phys.Sin.65 077801(in Chinese)[齐维靖,张萌,潘拴,王小兰,张建立,江风益2016物理学报65 077801]

[3]He J S,Zhang M,Pan H Q,Q i W J,Li P 2016 Acta Phys.Sin.65 167201(in Chinese)[何菊生,张萌,潘华清,齐维靖,李平2016物理学报65 167201]

[4]M av roid is C,Harris J J,Jackm an R B,Harrison I,Ansell B J,Bougrioua Z,M oerm an I 2002 J.App l.Phys.91 9835

[5]Jam es A F,Yeo Y K,Ryu M Y,Hengehold R L 2005 J. E lectron.M ater.34 1157

[6]Osinnykh I V,Zhu rav lev K S,M alin T V,Ber B Y, Kazantsev D Y 2014 Sem iconductors 48 1134

[7]Srikant V,Speck J S,C larke D R 1997 J.Appl.Phys. 82 4286

[8]Zhang Z,Zhang R,X ie Z L,Liu B,X iu X Q,Jiang R L, Han P,Gu S L,Shi Y,Zheng Y D 2008 Sci.China Ser. G:-Phys.M ech.Astron.51 1046

[9]D ing Z B,Yao S D,W ang K,Cheng K 2006 Acta Phys. Sin.55 2977(in Chinese)[丁志博,姚淑德,王坤,程凯2006物理学报55 2977]

[10]Look D C,Sizelove J R 2001 Appl.Phys.Lett.79 1133

[11]Look D C,Sizelove J R,K eller S,W u Y F,M ishra U K, DenBaas S P 1997 Solid State Comm un.102 297

PACS:72.10.Fk,72.20.Fr,73.20.Hb,81.70.–qDOI:10.7498/aps.66.067201

Determ ination of d islocation density of a class of n-GaN based on the variab le tem peratu re H all-eff ect m ethod∗

He Ju-Sheng1)†Zhang Meng2)Pan Hua-Qing3)Zou Ji-Jun4)QiWei-Jing2)Li Ping5)

1)(School of Science and Technology,Nanchang University,Nanchang 330029,China)
2)(School ofM aterial Science and Engineering,Nanchang University,Nanchang 330031,China)
3)(Departm ent ofM echanical Engineering,Shangrao Vocational and Technical College,Shangrao 334100,China)
4)(Engineering Research Center of Nuclear Technology App lication(East China Institute of Technology),M inistry of Education,

Nanchang 330013,China)
5)(M odern Education Technology Center ofNanchang University,Nanchang 330031,China)
(Received 23 O ctober 2016;revised m anuscrip t received 8 Decem ber 2016)

An analyticalm odel for electron m obility in a class ofwurtzite n-GaN,whose carrier concentration is over 1018cm−3(M ott’s critical lim it),is developed.W ith the dislocation density and two donor levels serving as the im portant param eters,the proposed model can accurately predict the electron mobility as a function of tem perature.The edge and screw dislocation densities in two sam p les,which are respectively grown on sapphire(001)by m etal organic chem ical vapor deposition and hydride vapor phase epitaxy,are determ ined by using thismodelwhich is discussed in detail.It is shown that the data-fi tting ofµH-T characteristic curve is a highly suitable technique for accurately determ ining the edge and screw dislocation densities in n-GaN fi lm s.Quantitative analyses of donor concentration and donor activation energy indicate that the im purity band occurswhen the carrier concentration is under 1017cm−3,much lower than the critical carrier concentration of M ott transition(1018cm−3).Such a behavior can also be confi rm ed by the results from solving the Boltzm ann transport equation by using the Rode iterativem ethod.Another anom aly is that the dislocation density in Mott transition material perhaps is lower than that ofmaterial w ith carrier concentration under 1018cm−3.This fact indicates that the cause of M ott transition should not be the shallow donor im purities around dislocation lines,but perhaps the deeper donor im purities or other defects.In the theoreticalm odel calculation,two transition characteristics together w ith the donor distribution and its energy equilibrium are taken into account.Based both on the Mott transition and the H-like electron statem odel,the relaxation energies for the shallow-donor defects along the screw and edge dislocation lines are calcu lated by using an electrical ensemble averagemethod.Besides,an assum ption that should be m ade is that there are 6 shallow-donor defect lines around one dislocation line.The research results show that the Hall m obility should be taken as the live degree of the ionizing energy for the shallow-donor defects along the dislocation line.The experimental results indicate that our calculation function can be best fi t by the experimental curve,w ith the values of dislocation density being between ourm odel and others determ ined by X-ray diff raction or by chem ical etching m ethod,which are all in good agreem ent w ith each other.Them ethod reported can be app lied to the wurtzite n-GaN fi lm s grown by various preparation technologies under any condition,w ith the peak-mobility tem perature about or over 300 K,whose Hallm obility near 0 K perhaps is over 10 cm2/(V·s)and even 100 cm2/(V·s).

gallium nitride,Hallmobility,dislocation density,Mott transition

10.7498/aps.66.067201

∗江西省自然科学基金(批准号:20151BAB 207066)和南昌大学科学技术学院自然科学基金(批准号:2012-ZR-06)资助的课题.

†通信作者.E-m ail:Hejusheng_2004@sohu.com

*Project supported by the Natural Science Foundation of Jiangxi Province,China(G rant No.20151BAB207066)and the Natu ral Science Foundation of College of Science and Technology of Nanchang University,China(G rant No.2012-ZR-06).

†Corresponding author.E-m ail:Hejusheng_2004@sohu.com