分层有耗手征介质中斜入射电磁波的传播矩阵∗
王飞1)2) 魏兵1)2)
1)(西安电子科技大学物理与光电工程学院,西安 710071)
2)(西安电子科技大学信息感知技术协同创新中心,西安 710071)
(2016年9月28日收到;2016年11月11日收到修改稿)
分层有耗手征介质中斜入射电磁波的传播矩阵∗
王飞1)2)†魏兵1)2)
1)(西安电子科技大学物理与光电工程学院,西安 710071)
2)(西安电子科技大学信息感知技术协同创新中心,西安 710071)
(2016年9月28日收到;2016年11月11日收到修改稿)
根据相位匹配条件,推导了平面电磁波斜入射情形下分层有耗手征介质中本征波复数波矢量的实部和虚部,二者方向不同使得在介质中传播的本征波为非均匀平面波.然后通过波矢量实部确定了介质中本征波的折射角.最后根据边界条件和本征波场方程给出了分层有耗手征介质中斜入射电磁波的传播矩阵,该传播矩阵可用于解析分析任意入射角情形下分层手征介质的反射透射和电波传播特性.
分层有耗手征介质,斜入射,传播矩阵
1 引 言
在电波传播、微波遥感和光学等多个领域,分层介质中电磁波的传播特性研究一直引人关注且具有普遍实用价值.而最近几年,手征超材料(chiralmetamaterials,CMM)的兴起再次引起了人们对电磁波与手征介质的相互作用问题的浓厚兴趣.手征介质具有的手征性(chirality)是指平移和旋转都不能使一个物体和其镜像完全重合的性质,除人工CMM外,自然界中的螺旋结构高分子化合物及DNA螺旋结构等都具有手征性.不同于一般介质,手征介质中的电场和磁场是耦合的,其中传播的本征电磁波是右、左旋圆极化波,这使得通过其中的电磁波极化面发生旋转[1−3],这一特性使其在微波天线阵列、天线罩、微带线基片和波导等方面有着广泛的应用.分层手征介质中电波传播特性的解析分析方法研究,对于手征介质天线设计、CMM设计、手征参数反演等都具有重要意义. 1988年,Basiri等[4]解析分析了手征介质界面对平面电磁波的反、透射并给出了手征介质中的本征波场表达式;随后,很多国外学者先后将矢量电路[5], Wentzel-K ramers-Brillouin近似[6]、谱域并矢格林函数[7]、矢量传输线[8],4×4矩阵[9]、并矢格林函数[10]、调和格林函数[11],Mueller矩阵[12]等解析分析方法推广应用于层状手征介质;国内学者利用传播矩阵[13]、传输线理论[14]、不对称传输线模型[15]分析了电磁波正入射分层手征介质问题;张援农等[16]用传播矩阵分析了无耗分层手征介质的光子带隙特性.
Engheta等[17]和Lindell等[1]的研究表明,手征介质都具有频率色散特性,其电磁参数一般为频率的复数函数.这使得在手征介质中传播的右、左旋圆极化本征波的波矢量和波数一般为复数,即手征介质一般是有耗的.因此,当平面电磁波从空气斜入射到手征介质中时,由于相位匹配,手征介质中波矢量的实部和虚部方向不同.波矢量实部方向为相位传播方向,而虚部方向为振幅传播方向,二者不同使得这时在手征介质中传播的本征波为非均匀平面波.本文首先根据相位匹配条件,推导了平面电磁波斜入射分层有耗手征介质时介质中本征波复数波矢量的实部和虚部,并依此计算出本征波的折射角;然后根据边界条件和本征波场方程推导了分层有耗手征介质中斜入射电磁波的传播矩阵,该传播矩阵可用于解析分析任意入射角情形下分层手征介质的反射透射和电波传播特性.
2 手征介质的本构关系和本构参数
手征介质(Paster介质)的本构关系可写为[1]
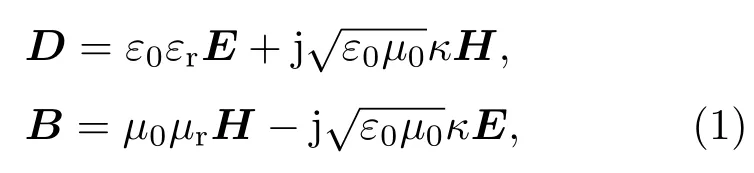
其中ε0和µ0分别是真空介电系数和磁导率,εr和µr分别是手征介质的相对介电系数和相对磁导率,κ是手征参数.(1)式称为手征介质本构关系的EH表述.1990年,Engheta和Zablocky[17]为了确定手征介质的瞬态响应而研究手征介质的K ramers-K ronig关系时,将手征介质的本构关系写为
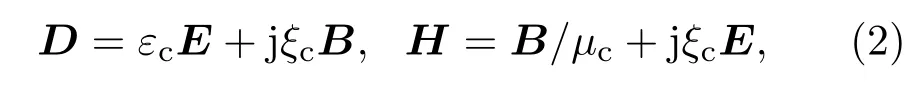
(2)式称为手征介质本构关系的EB表述,其中ξc称为手征导纳.根据(1)和(2)式可得两种表述中本构参数的关系为

Engheta和Zablocky[17]证明手征导纳ξc为频率的复函数,因此根据(3)式可知手征参数κ也是频率的复函数,其实部和虚部分别代表了手征介质的旋光色散(optical rotatory dispersion,ORD)和圆二色性(circular dichroism,CD).Lindell等[1]进一步研究证明相对介电系数εr和相对磁导率µr也必是频率的复函数.因此对手征介质,不论是EH表述下的本构参数εr,µr,κ,还是EB表述下的本构参数εc,µc,ξc,都是频率的复函数,即介质各个参数皆为复数.
3 分层手征介质
考虑由n层不同参数手征介质构成的分层结构置于真空(或空气)中的情况,如图1所示.设介质层各分界面垂直于z轴(平行于xoy平面),沿z轴正方向分别为第1层到第n层,分别设为介质1到介质n,介质层左侧和右侧的真空区域分别设为介质0和介质t.第1层(介质1)与真空(介质0)分界面坐标为z=d0=0;往后各分界面坐标为z=d1,d2,···,dn;z=dn为最后一层(介质n)与真空(介质t)分界面坐标.设各层手征介质的电磁参数分别为εrl,µrl,κl(l=1,2,···,n).
设平面电磁波从介质0区域(真空)斜入射到该手征介质层,入射面为xoz平面,这时介质0区域为入射波和反射波区域,介质层另一侧的介质t区域为透射波区域,如图1所示.入射角、反射角、透射角分别设为θi,θr,θt.此时,在介质层中的各个区域内都同时存在前向行波(右行波)和后向行波(左行波),另外由于介质的手征特性,各行波都包含两个本征波:I型本征波即右旋波和II型本征波即左旋波.设各个区域中前行波的两个本征波传播方向与z轴的夹角分别为θl1和θl2,即为两个本征波的折射角.
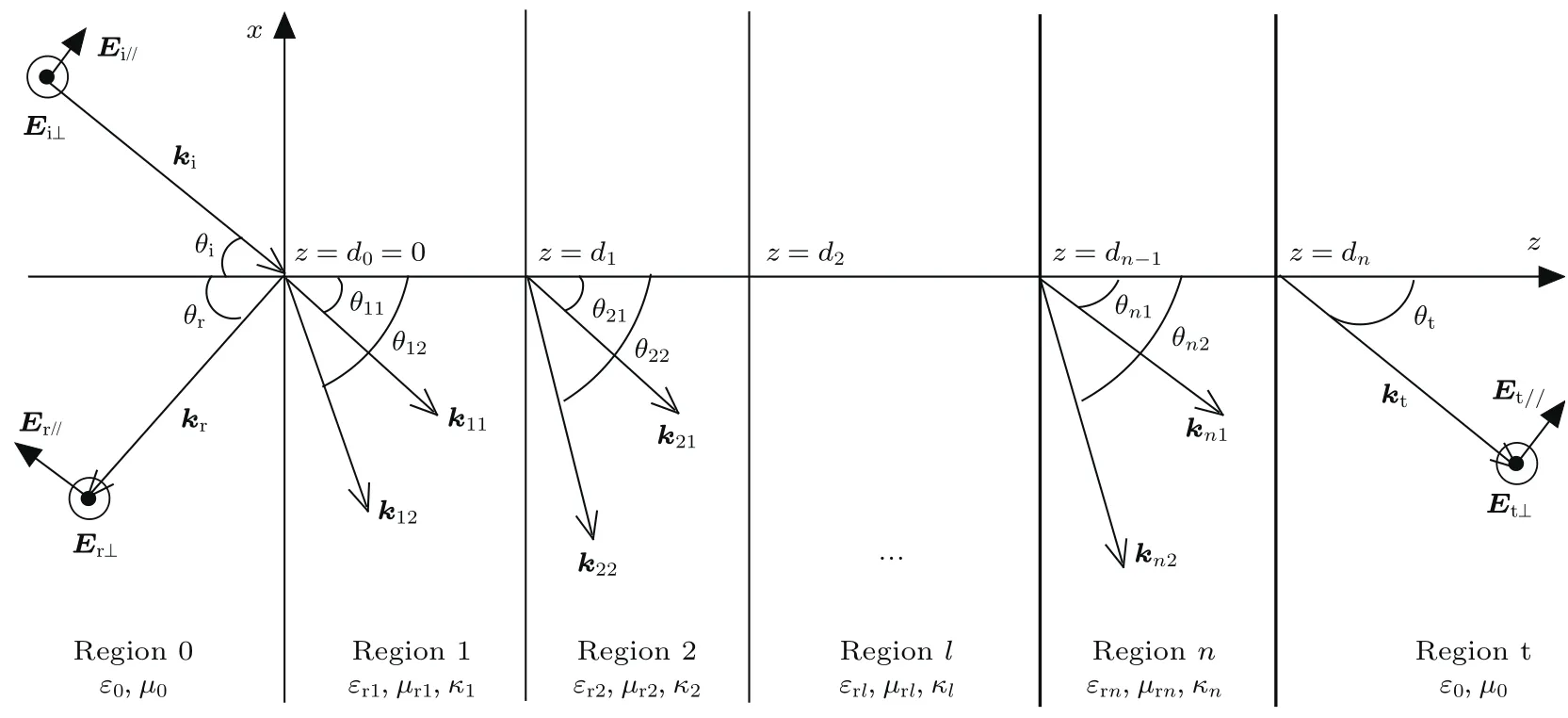
图1 层状手征介质Fig.1.Stratified chiralm ed ia.
3.1 各介质区域内的波矢量
由于介质0和介质t为真空,波数k0=为实数.所以入射波、反射波、透射波的波矢量分别为
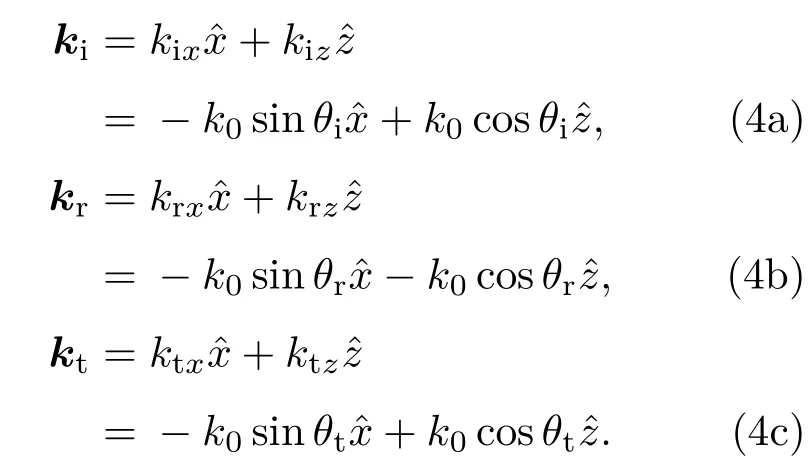
根据相位匹配原理[18],各层波矢量的x分量相等,记为kx,则由(4)式可知
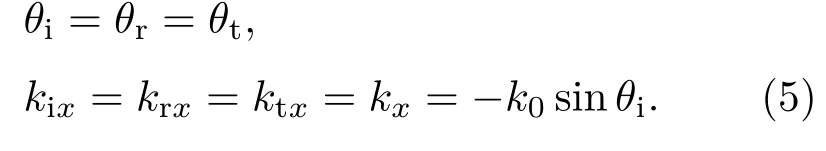
在介质1到n各个区域为手征介质,其波数为[1]
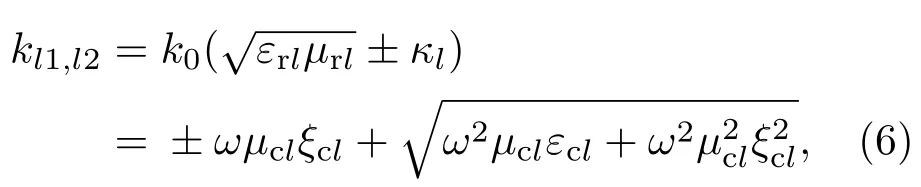
其中kl1和kl2分别表示介质l中I型和II型波波数, I型波取+号,II型波取−号.由于手征介质参数为复数,所以其中的波数和波矢量一般亦为复数.设介质l中前行的I型和II型本征波波矢量分别为kl1和kl2,并写为
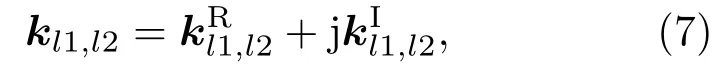
上标R,I分别表示实部和虚部.由于各层波矢量的x分量相等,因此有
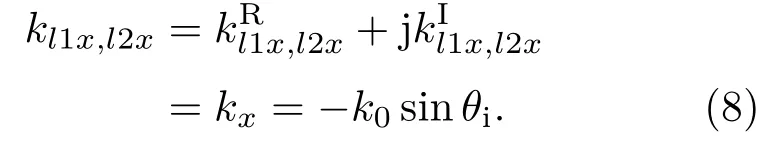
所以在手征介质层中,波矢量的虚部x分量为0,只有z分量,波矢量可写为
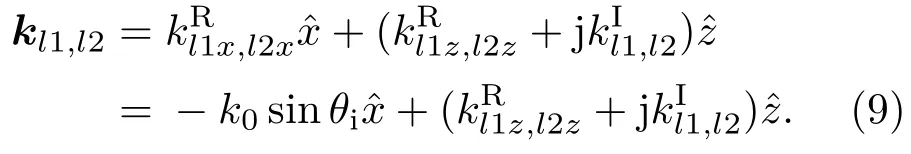
由(9)式可得
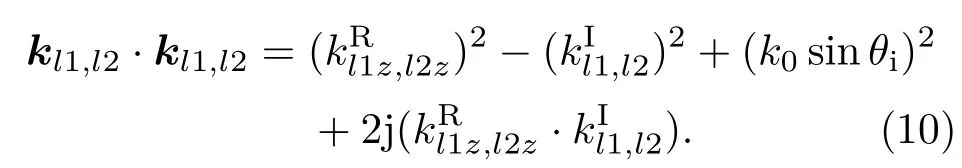
又根据(6)式有

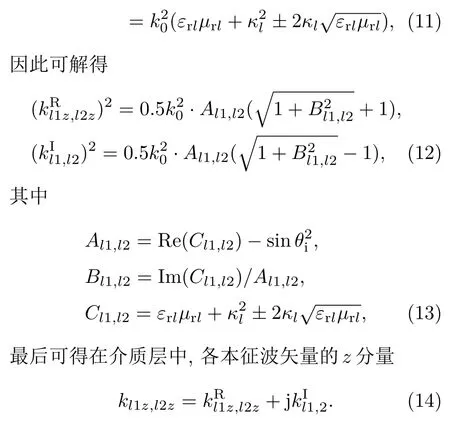
3.2 各介质层中本征波的折射角和波阻抗
由于各介质层中波矢量的虚部只有z分量,所以波的等振幅面垂直于z轴.波矢量的实部既有z分量又有x分量,不同介质层中波矢量实部的x分量相等.波矢量实部的方向为相位传播方向,由前面给出的波矢量实部z和x分量可以得到各介质层中本征波的折射角的余弦为
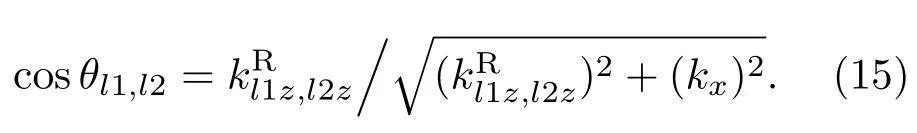
介质0和介质t区域为真空,波阻抗Z0=Zt=为实数.在介质1到n各个区域为手征介质,其波阻抗为复数[1]
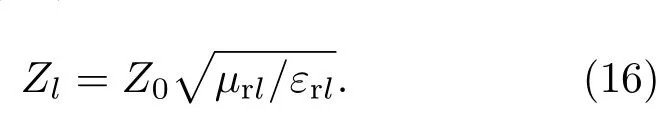
定义l层和l+1层的相对复数波阻抗为
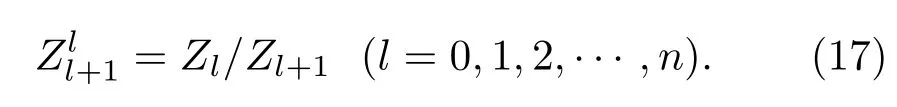
4 分层手征介质传播矩阵
4.1 介质层中各层内部的传播矩阵
一般地,第l(l=1,2,···,n)层手征介质中前向和后向传播的电磁波为[4](简单起见,略去时谐因子exp(−jωt),下同)
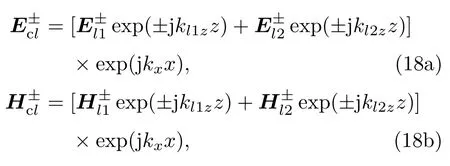

图2 平面波斜入射层状手征介质Fig.2.Oblique incidence on stratified chiralm edia.
其中
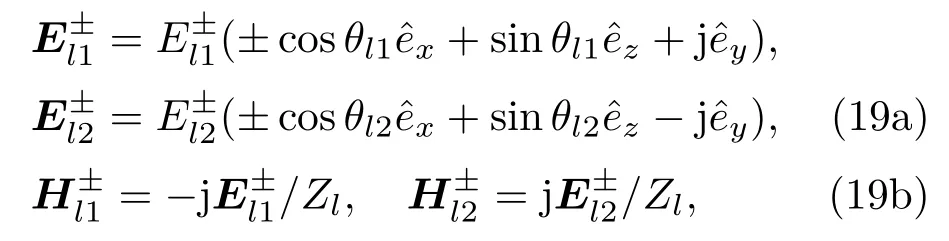
下标1,2表示I型(右旋)波和II型(左旋)波,上标±表示前向和后向行波.
根据(18)式可知,I,II型波的前向和后向行波电场在Nl和Ml点(图2)处的关系为
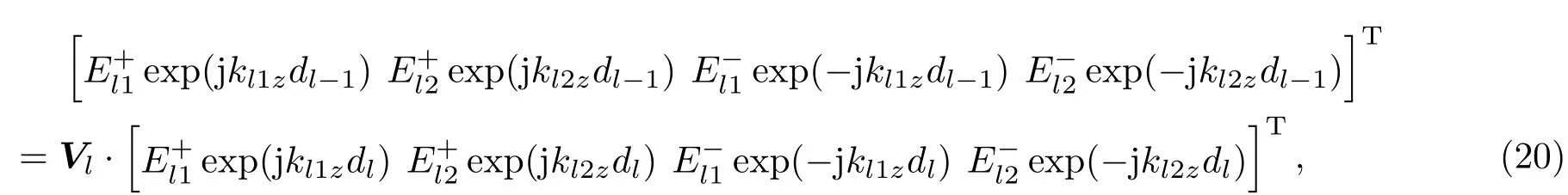
其中
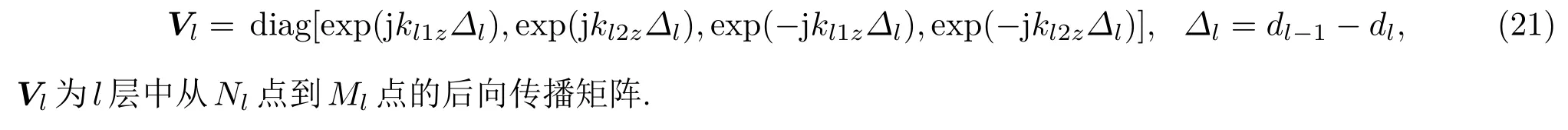
4.2 介质层中各分界面两侧的传播矩阵
如图2所示,Ml+1和Nl分别为第l和l+1层分界面(z=dl)前侧和后侧的观察点,根据边界条件[18],两点处电、磁场切向连续,则由(18)和(19)式可得
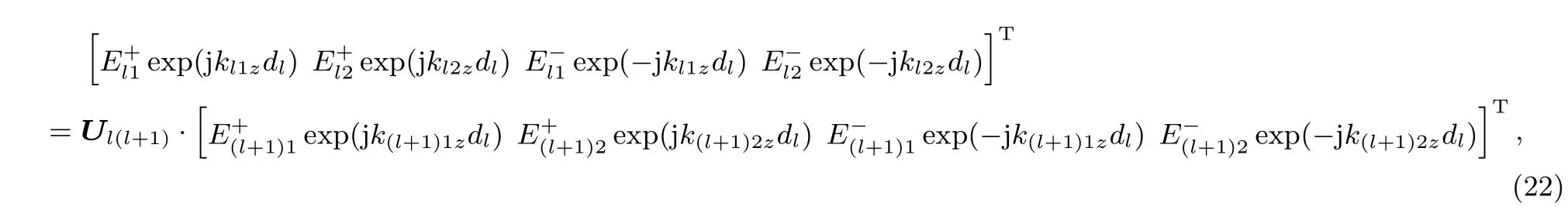
其中

为l和l+1层分界面z=dl两侧从Ml+1点到Nl点的后向传播矩阵.
4.3 入射界面处的后向传播矩阵
在入射区(介质0)存在入射波和反射波,入射波为前向行波,可表示为[4]
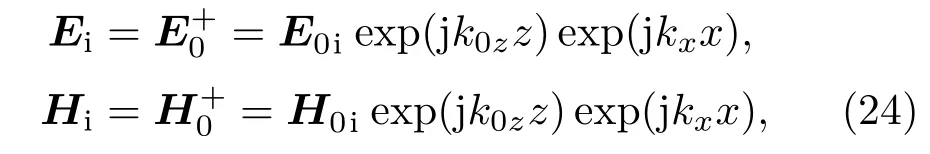
其中
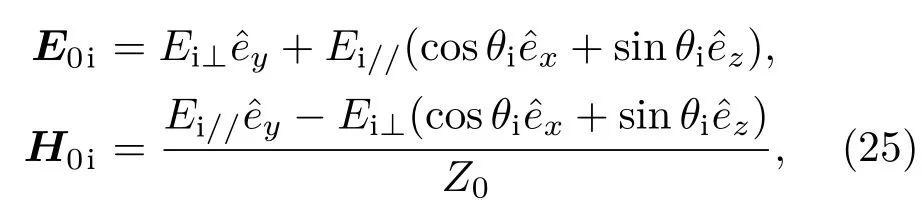
反射波为后向行波,可表示为[4]
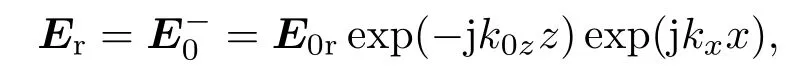
其中
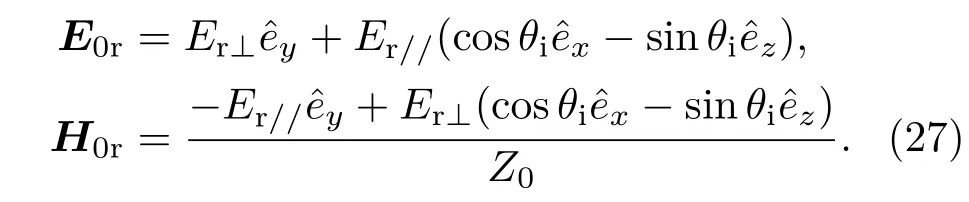
根据边界条件,在介质0和介质1分界面z=d0=0处,界面前侧M1点处的场和界面后侧N0点处(图2)的场有如下关系:
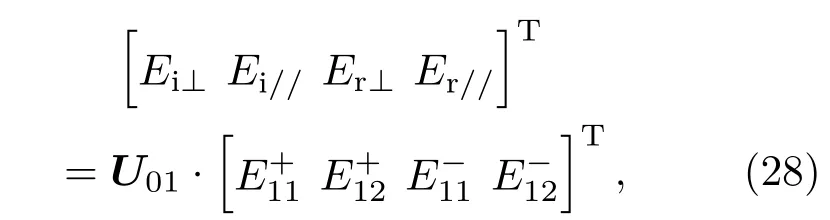
其中
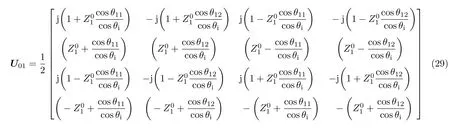
为介质0和介质1分界面z=d0=0处,界面两侧从M1点到N0点的后向传播矩阵.
4.4 透射界面处的后向传播矩阵
在透射区(t)只有透射波,为前向行波,无后向行波.透射波可表示为[4]
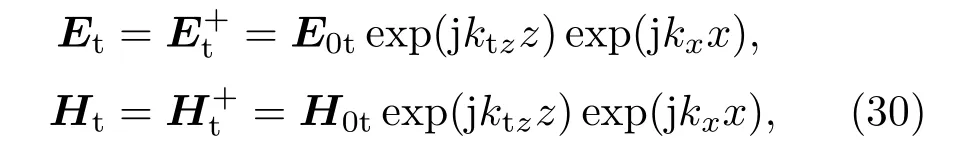
其中

根据边界条件,在介质n和介质t分界面z=dn处,界面前侧Mt点处的场和界面后侧Nn点处(图2)的场有如下关系:
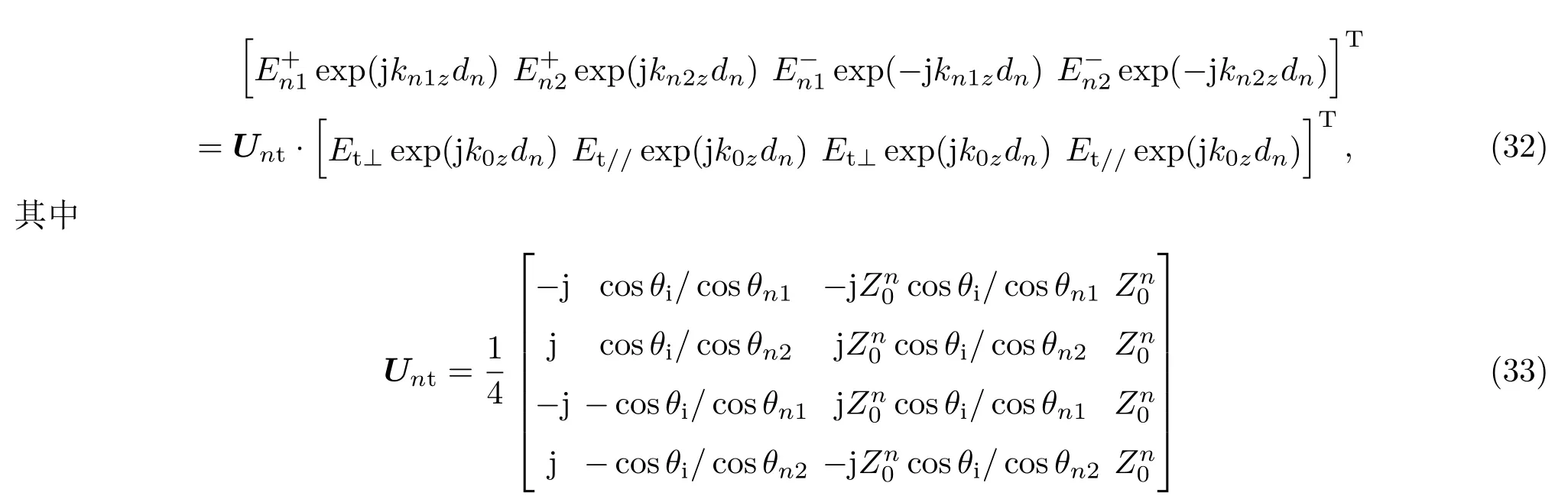
为介质n和介质t分界面z=dn处,界面两侧从Mt点到Nn点的后向传播矩阵.
4.5 后向传播矩阵
综合上述讨论分析可得图2中从Mt点到N0点的传播用传播矩阵表示为
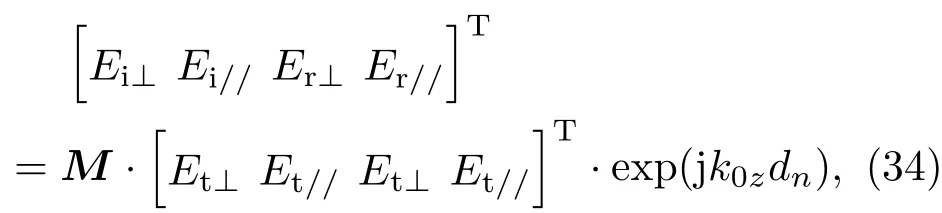
其中
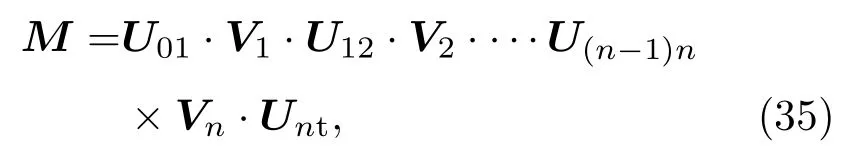
即为后向传播矩阵.
5 线极化波入射时的反射透射系数计算
传播矩阵M为4×4矩阵,设其元素为mij(i,j=1,2,3,4).根据(34)式可解得反射电场和透射电场用入射电场的表示,
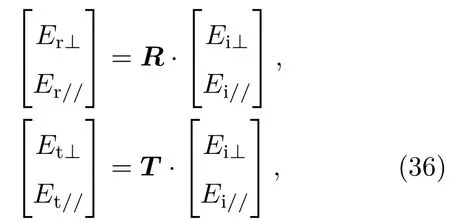
其中反射矩阵R和透射矩阵T分别为
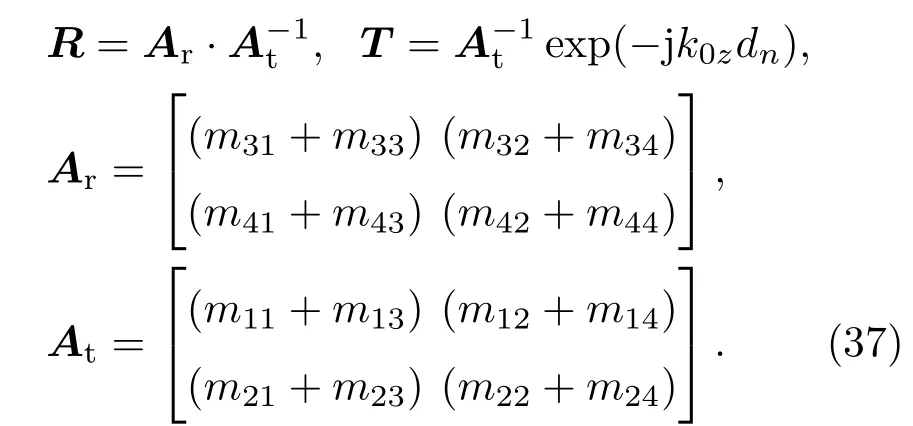
设入射线极化平面波波幅为E0,分别讨论TE波入射和TM波入射时,分层手征介质的同极化和交叉极化反射透射系数的计算.入射波为TE波时,入射电场平行分量为0;入射波为TM波时,入射电场垂直分量为0,即
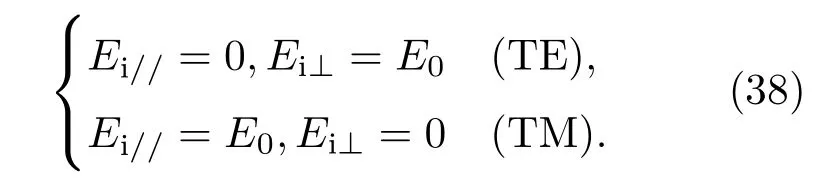
将(38)式代入(36)式可得TE波、TM波同极化和交叉极化反射、透射系数分别为
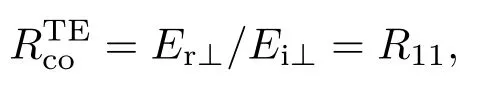
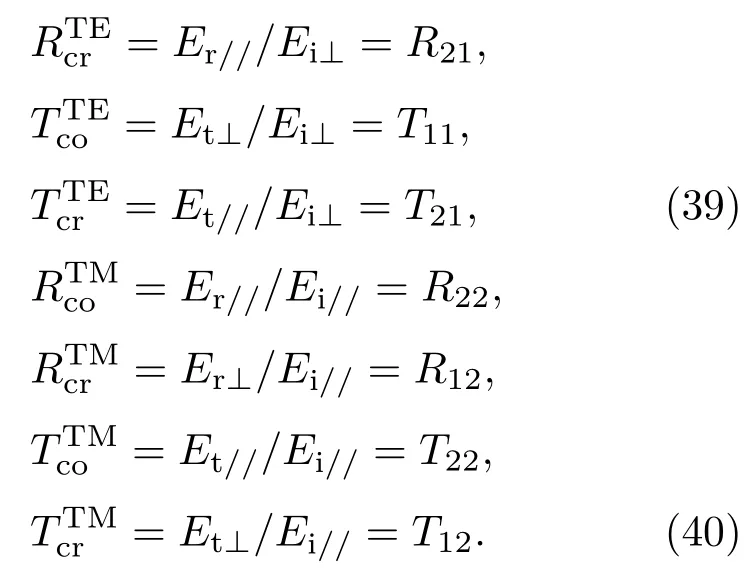
6 算 例
6.1 色散手征介质层的反射和透射系数
无限大色散手征介质层厚度d=0.1 m,介电系数和磁导系数为Lorentz模型,手征参数为Condon模型
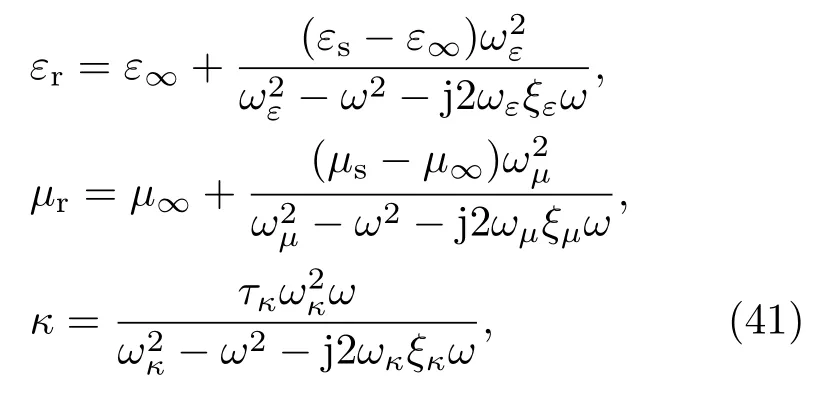
其中ε∞=2,εs=5,ωε=4π×109,ξε=0.5, µ∞=1.1,µs=1.8,ωµ=4π×109,ξµ=0.5, ωκ=4π×109,ξκ=0.3,τκ=0.5/ωκ.设线极化平面波垂直入射该色散手征介质层,图3中的划线和实线分别表示利用本文传播矩阵方法计算得到的反射系数Rco,Rcr和透射系数Tco,Tcr的幅值;同时我们又采用时域有限差分(FDTD)方法[19]计算该介质层对入射脉冲的时域响应并通过傅里叶变换得到频域反射透射系数,计算结果在图3中用十字和叉表示,可见二者非常符合.
线极化波进入手征介质后分解为左、右旋两个圆极化本征波,由于ORD特性,两本征波的相速不同,使波的极化方向发生旋转,而CD又使两本征波的衰减不同,因此线极化波进入手征介质后成为椭圆极化波,反射波和透射波的极化方向都发生变化,只有当垂直入射时,由于手征介质的互易性[12,20,21],反射波与入射波极化方向相同,交叉极化反射系数为0(如图3(b)所示).
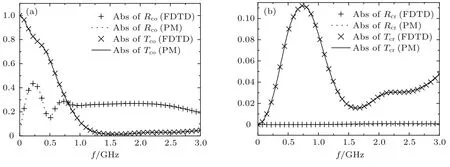
图3 色散手征介质层的反射透射系数幅值 (a)同极化反透射;(b)交叉极化反射透射Fig.3.The am p litudes of refl ection and transm ission coeffi cients for a d ispersive chiral layer:(a)The co-polarized refl ection and transm ission;(b)the cross-polarized refl ection and transm ission.
6.2 四重旋转Ω单元结构CM M平板的反射和透射系数
文献[22]反演了一种四重旋转Ω单元结构CMM平板的本构参数,其表达式为
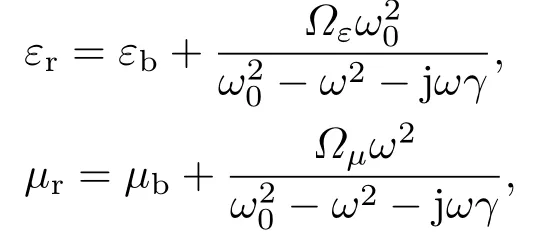
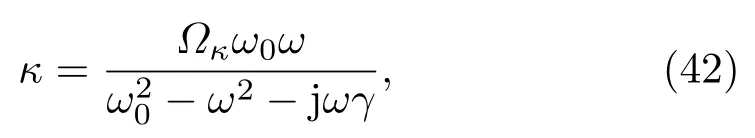
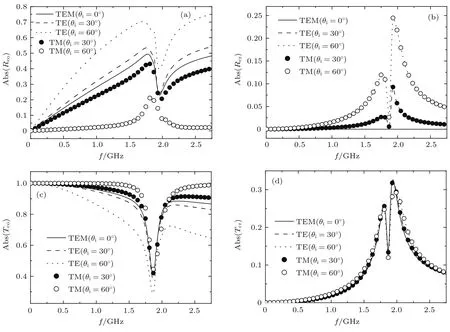
图4 四重旋转Ω单元结构CMM平板的反射和透射系数幅值 (a)同极化反射;(b)交叉极化反射;(c)同极化透射;(d)交叉极化透射Fig.4.The am p litudes of refl ection and transm ission coeffi cients for the four-folded rotated-particle CMM slab:(a)The co-polarized refl ection;(b)the cross-polarized refl ection;(c)the co-polarized transm ission; (d)the cross-polarized transm ission.
其中ω0=1.8713 THz,γ=0.05463ω0,εb= 3.1736,µb=0.9798,Ωε=0.156,Ωµ=0.0625,Ωκ=0.0993,板厚度为d=12µm.利用本文传播矩阵方法计算了线极化平面波入射该手征介质平板时的反射和透射系数,如图4所示,图4(a)—(d)分别是同极化、交叉极化反射系数Rco,Rcr和透射系数Tco,Tcr的幅值,其中实线为垂直入射情形,划线和点线表示TE波在30◦和60◦斜入射时情形,实心和空心圆圈表示TM波在30◦和60◦斜入射时情形.由图可见,由于手征介质的互易性[12,20,21],交叉极化反射、透射系数幅值与入射波极化状态无关,而且垂直入射时的交叉极化反射系数为0.同时,反射透射系数在频率ω0=1.8713 THz处有较强振荡.
6.3 周期分层手征介质的反射和透射系数
一周期分层结构位于空气中,它由(εc1,µc1,ξc1)和(εc2,µc2,ξc2)两种非磁性手征介质交替排列而成,每层厚度相等为d=180 nm,介质参数为µc1=µc2=µ0,εc1=(6.55−0.16j)ε0, εc2=(1.75−0.27j)ε0和ξc1=ξc2=1×10−3−j× 2×10−4(S),共22层.利用本文传播矩阵方法计算了线极化平面波入射该分层结构的反射和透射系数,如图5所示.图5(a)—(d)分别是同极化、交叉极化反射系数Rco,Rcr和透射系数Tco,Tcr的幅值,其中实线为垂直入射的情形,划线和点线表示TE波在30◦和60◦斜入射时的情形,实心和空心圆圈表示TM波在30◦和60◦斜入射时的情形.由图可见,在红外区域存在光子带隙,且光子带隙的位置和宽度与入射波的极化状态和入射角都有关系,这使得对同一结构,可以通过控制入射极化状态和入射角实现光子带隙调节.
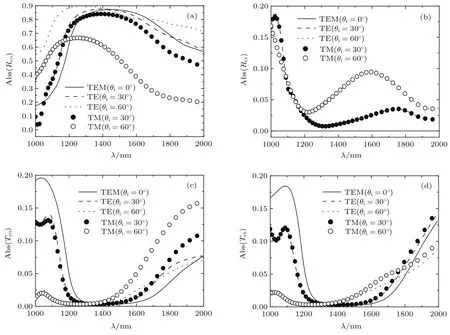
图5 周期分层手征介质的反射和透射系数幅值 (a)同极化反射;(b)交叉极化反射;(c)同极化透射;(d)交叉极化透射Fig.5.The am p litudes of refl ection and transm ission coeffi cients for the period ic layered chiral m edia:(a)The co-polarized reflection;(b)the cross-polarized reflection;(c)the co-polarized transm ission;(d)the cross-polarized transm ission.
7 结 论
由于手征介质的色散特性使其一般为有耗介质,因此当平面电磁波斜入射层状手征介质时,介质中传播的平面本征波为非均匀波.本文首先利用相位匹配条件推导了层状手征介质中本征波复数波矢量的实部和虚部,并利用波矢量实部计算本征波折射角,然后根据边界条件和本征波场方程给出计算层状手征介质中斜入射电磁波的的传播矩阵,利用该传播矩阵计算了单层和多层手征介质的反射和透射系数.该传播矩阵可以用来解析分析斜入射、有耗等条件下电磁波在层状手征介质中的传播特性,同时由于可以通过令手征参数κ=0将手征介质退化为一般介质,所以该传播矩阵同样适用于一般的层状介质或一般介质与手征介质复合层状结构.此外,除了计算反射透射这样的正问题,可以进一步研究利用传播矩阵分析逆问题——通过实验测量得到的反射和透射矩阵反演手征介质参数,这在CMM结构设计和等效参数反演中将具有重要的实用价值和意义.
[1]Lindell IV,Sihvola A H,Tretyakov S A,V iitanen A J 1994 E lectrom agnetic W aves in Chira l and Bi-isotropic M edia(Boston:A rtech House)pp1–15
[2]W ang M Y,Li G P,Zhou M,W ang R,Zhong C L,Xu J,Zheng H 2014 Int.J.Num er.M odel.27 109
[3]Taup ier G,Boeglin A,Crégut O,M ager L,Barsella A, Gąsior K,Rehsp ringer J L,Dorkenoo K D 2015 Opt. M ater.45 22
[4]Bassiri S,Papas C H,Engheta N 1988 J.Opt.Soc.Am. 5 1450
[5]Oksanen M I,Tretyakov S A,Lindell IV 1990 J.Electrom agnet.W aves Appl.4 613
[6]V iitanen A J,Lindell IV,Sihvola A H 1991 J.E lectrom agnet.W aves Appl.5 1105
[7]Sam iM A,Tarek M H,Kong J A 1992 J.Opt.Soc.Am. A 9 413
[8]Lindell IV,Tretyakov S A,Oksanen M I 1993 J.E lectrom agnet.Waves Appl.7 147
[9]Ivanov O V,Sem entsov D I 2000 Crysta llography Rep. 45 487
[10]Li L W,Yeap S B,Leong M S,Yeo T S,Kooi P S 2002 Prog.Electrom agnet.Res.35 53
[11]Pau l E C,Ezekiel B 2005 Canadian J.Phys.83 1265
[12]Bahar E 2007 J.Opt.Soc.Am.B 24 1610
[13]Y in W Y,W an W 1993 J.E lectron.15 287(in Chinese) [尹文言,万伟1993电子科学学刊15 287]
[14]Liu Z S,Song L R,Fu G X 1999 J.M icrowaves 15 339 (in Chinese)[刘述章,宋俐荣,符果行1999微波学报 15 339]
[15]X iao Z Y,W ang Z H 2003 Chin.J.Radio Sci.18 687 (in Chinese)[肖中银,王子华2003电波科学学报18 687]
[16]Zhang Y N,Zhao Z Y,Huang T C,Jiao P N 2004 Chin. J.Radio Sci.19 537(in Chinese)[张援农,赵正予,黄天锡,焦培南2004电波科学学报19 537]
[17]Engheta N,Zab locky P G 1990 E lectron.Lett.26 2132
[18]Kong J A 2002 Electrom agnetic Wave Theory(Beijing: H igher Education Press)pp23,103
[19]W ang F,W ei B,Li L Q,Cao L,Yang Q 2015 Proceedings of2015 Cross Strait Quad-Regional Radio W ireless Conference Xi’an,China,August 12–15,2015 p67
[20]Dem ir V,E lsherbeniA Z,Ercum ent A 2005 IEEE Trans. An tennas Propag.53 3374
[21]Zarifi D,Soleim aniM,Abdolali A 2013 IEEE Trans.Antennas Propag.61 5658
[22]Zhao R K,Koschny T,Soukou lis C M 2010 Opt.Express 18 14553
PACS:41.20.Jb,42.25.Bs,78.20.CiDOI:10.7498/aps.66.064101
P ropagation m atrix o f p lane w ave inciden t ob liquely on stratifi ed lossy ch iralm ed ium∗
Wang Fei1)2)†Wei Bing1)2)
1)(School of Physics and Optoelectronic Engineering,X idian University,X i’an 710071,China)
2)(Collaborative Innovation Center of Inform ation Sensing and Understanding at X id ian University,X i’an 710071,China)
(Received 28 Sep tem ber 2016;revised m anuscrip t received 11 Novem ber 2016)
The real and im aginary parts of the eigen com p lex wave vector in a stratified lossy chiralm edium for the case of ob lique incidence are derived by using the phase-m atching condition.Due to the fact that the real and im aginary parts are nonparallel,the eigen wave propagating in the medium is inhomogeneous.Then the refraction angle of the eigen wave can be deduced via the real part of the wave vector.Finally the propagation m atrix of the obliquely incident wave in a stratified lossy chiralm edium is derived based on the boundary conditions and the field equations of eigen wave in each region.By using the p roposed method,the reflection,transm ission,and p ropagation characteristics of p lane wave w ith arbitrary incident angle in a stratified chiralmedium can be analyzed.
stratified lossy chiralmedia,oblique incidence,propagation matrix
10.7498/aps.66.064101
∗国家自然科学基金(批准号:61401344,61571348)和中国国家留学基金(批准号:201606965055)资助的课题.
†通信作者.E-m ail:w fei79@163.com
*Project supported by the National Natural Science Foundation of China(G rant Nos.61401344,61571348)and the State Scholarship Fund of China(G rant No.201606965055).
†Corresponding author.E-m ail:w fei79@163.com

