一种基于核值的R O U S T I D A算法

辽宁石化职业技术学院 杨 迪

一种基于核值的R O U S T I D A算法

辽宁石化职业技术学院 杨 迪

无论是ROUSTISA算法还是其修正算法，都具有反应速度快、运算简单、对于相似或相同决策处理能力较强等优点。并且修正后的算法还可避免不相容决策，具有较好的实用价值。但是从属性约简的过程可知，并非任何一个数据对于决策的作用都一样，在基于粗糙集的属性约简过程中，核值才是最有用的数据，然而上述算法将所有数据同等对待，并未体现出核值的重要性。

核值；ROUSTIDA算法；可辨识矩阵

一、基于核值的ROUSTIDA算法

该算法是以可辨识矩阵为基础，基本流程如下：

步骤一核值化：

步骤三：

步骤四决策表中对象独立性的判断：

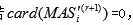
步骤五如果信息还有遗失值，可用平均值等方法填充；

步骤六结束。

二、基于核值的ROUSTIDA算法实现过程

对于整个算法的实现，通过实验将更易于理解。算法实际上是要实现“将不完备的数据矩阵进行数据填补，最终得到一个完整的数据矩阵”这一功能。以下我将通过一个简单的例子来逐步介绍该算法的实现过程。

程序实现过程如下：

第一步，程序要有一个输入矩阵的过程。由外部输入一个不完备的矩阵S1，假设输入的数据如表1所示：（*表示为缺失的数据）

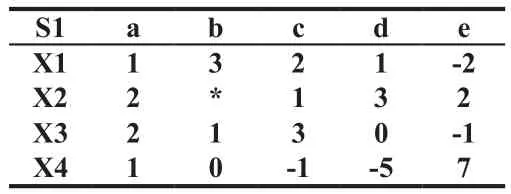
表1 初始矩阵

表2 待补矩阵

第二步，要分析、处理数据，目的是要按照要求，将不完备信息系统分离成其极大完备子系统和待补系统。

首先要得到一个待补矩阵S2（即保留所有空值*所在的行和列的数据,其余的数据均用*来表示），和一个去掉空值*所在的行和列后所得的分析矩阵S3，划掉的数据用*表示，S3就是用来确定极大完备矩阵的。

仍以上面的矩阵为例，所得的S2和S3如表2所示：

表3 分析矩阵

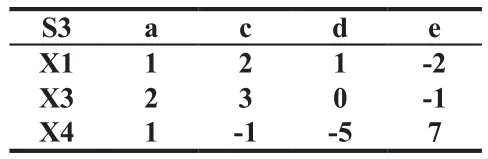
表4 改写分析矩阵

为方便对S3求秩，也可将S3写成下面的形式，如表4所示。

得到了S2和S3之后，开始对S3进行分析，求S3的秩（即看S3是几阶的），将其化为阶梯矩阵，得到S3’。

如上例分析，所得的S3’的矩阵如表5所示。

表5 阶梯矩阵

表6 核值矩阵

即所得的矩阵为2阶矩阵。据此，对S3求得极大完备矩阵S4。我们只需随机选择其中的一个极大完备矩阵作为核值矩阵S5即可。假设我们选择的是下述矩阵，如表6所示。

然后，将S5与S2合并，得到一个新的矩阵S6。

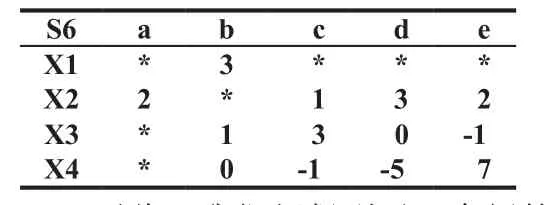
表7 合并矩阵

表8 辨析表

至此，我们便得到了一个新的不完备信息系统，而此信息系统就是基于核值的信息系统。接下来将以此信息系统为填补对象，来进行后续的操作。

第三步：填补数据。

对所得矩阵S6中的缺失项进行填补（通过循环比较S6中的任意两行i和j,看i行与j行是否不可分辨）。

如上例的辨析结果如如表8所示。

由此可见X1行与X2行为不可分辨关系，所以，我们将X1行与X2行中的空值元素替换为其对应的非空元素值，得S6’，进行了一次填补。填补结果如如表9所示：

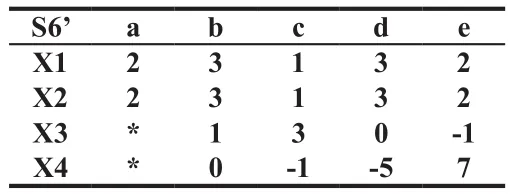
表9 初次填补

表1 0 填补完成表

对S6’重复第三步内容，直到循环结束。如果循环结束后仍有“*”值存在，则可利用均值法或最大频率法等来进行填补。

第四步：将初始矩阵S1中的缺失元素*替换填补为矩阵S7中对应位置的非空元素。至此，对不完备矩阵的填补结束。程序最终输出一个完备的矩阵，如表10所示。

整个算法的实现就是通过上述过程来体现的。既证明了算法的优势，在保留原有数据的同时，有效的填补了缺失信息，避免了决策冲突；同时也发现对于程序设计所带来的时间复杂度和空间复杂度较高，使得程序的运行效率偏低。

[1]饶晶晶．基于ROUSTIDA算法改进的RFID数据清洗技术[J]．信息与电脑：理论版,2016 (8)：93-94．

[2]关莹,苏贵斌,康熠华．一种改进的ROUSTIDA数据填补方法[J]．软件导刊,2016,15(11)：12-14．

杨迪（1980—），男，满族，辽宁锦州人，硕士，讲师，主要从事应用数学及图论的研究。