核电安全注入系统可靠性评估方法研究
沈 维,陆 彬,羊冰清,景亚杰,朱小良
(东南大学 能源与环境学院,南京 210096)
核电技术
核电安全注入系统可靠性评估方法研究
沈 维,陆 彬,羊冰清,景亚杰,朱小良
(东南大学 能源与环境学院,南京 210096)
为了研究安全注入系统的可靠度,在现有的核电机组运行基础上,结合神经网络、极大似然估计及支持向量机等数值方法,构建了安注系统的设备可靠性计算模型,通过推算设备的可靠性,并运用可靠度数学模型进行系统的可靠性评估。通过比较核电的实时运行数据结果,验证了方法的可行性,为系统可靠性评估提供了理论手段。
核电; 安全注入系统; 数值方法; 数学模型; 可靠性评估
安全注入系统[1]是核电机组专设安全设施中的一个重要系统,当反应堆冷却剂系统发生失水事故时,安全注入系统能够完成应急堆芯冷却功能,保证反应堆迅速安全停堆,因此对该系统进行可靠性评估具有重要意义。
设备是系统的组成单元,所以系统的可靠性可以从设备上体现。由于一个系统内包含的设备种类比较多,而且人们在短期内是无法判断设备的磨损程度的,数值方法可以直观地表征设备和系统的可靠度,从而对系统的安全性有量化的判断,因此可以通过数值方法,获得设备的可靠度,再根据可靠度数学模型得到系统可靠性的评估。国内外在核电系统可靠性研究上,还没有形成完善的理论体系[2],仅仅停留在单个设备的可靠性研究上,如贝叶斯方法[3]、Bootstrap[4]法、雨流法[5]等,而且系统远比设备复杂,这些方法虽有可借鉴之处,但无法直接应用,安全注入系统[6]只有基于故障树的故障诊断,对安全注入系统的可靠度并未做深入研究。
笔者以我国自主设计、自主建设的某核电机组的安全注入系统为研究对象,基于现有核电机组的运行历史数据,运用数学模型,通过Matlab编写了系统可靠性评估程序,以图表的形式表征系统的可靠性,并与实际论证结果相比较。
1 计算模型
1.1 可靠性分布模型
对于机械设备的可靠性评估,目前采用的主要模型是威布尔分布[7]模型。威布尔模型对各种数据拟合能力比较强,能够比较全面地体现设备失效情况。
故障概率密度函数:
(1)
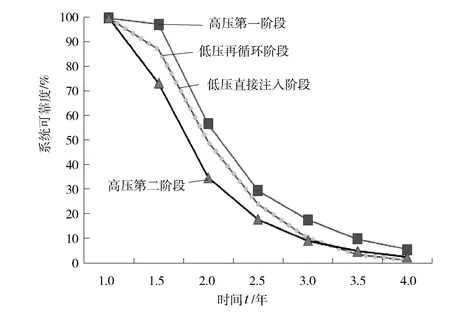
式中:λ(t)为失效率;R(t)为可靠度函数;β>0为形状参数;η>0为尺度参数。形状参数β不同时,其f(t)曲线的形状不同,当β=1时,曲线接近指数分布;当β=2时,曲线接近瑞利分布;当β∈(3,4)时,曲线接近于正态分布。
可靠度函数:
(2)
且满足:R(t)+F(t)=1。
1.2 参数估计模型
威布尔分布函数的未知参数有形状参数β和尺度参数η,只有确定形状参数和尺度参数的数值后,才能充分利用分布模型,但由于样本数据较小,只有通过不同方法的拟合,得到最佳参数估计值。笔者运用了线性回归、支持向量机、极大似然估计3种数值方法进行拟合,通过比较均方根误差,得到最优参数估计值。
1.2.1 线性回归估计法
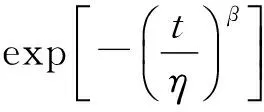
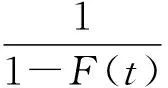
(3)
令:
可得:
y=wx+b
(4)
则式(4)是所求拟合曲线的形式。w为斜率;β为形状参数;η为尺度参数;b为截距。
1.2.2 支持向量机法
支持向量机法[9]的主要思想是建立一个分类超平面作为决策曲面,使得正例和反例之间的隔离边缘被最大化,即支持向量机是结构风险最小化的近似实现。C-SVC模型是比较常见的二分类支持向量机模型,其具体形式如下:
(1) 已知训练集:
T={(x1,y1),L,(xl,yl)}∈(X×Y)l
(5)
式中:xi∈X=Rn,yi∈Y={-1,1},i=(1,2,L,l)。xi为特征向量。
(2) 选取适当的函数K(x,x′)和适当的参数C,构造并求解最优化问题:
使得:
得到最优解
(6)
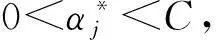
(7)
(4) 构造决策函数
(8)
1.2.3 极大似然估计法
极大似然估计法是在总体类型已知条件下使用的一种参数估计方法,是利用总体密度或概率分布的表达式及子样所提供的信息来求未知参数的估计量。对于二参数的威布尔分布,未知参数有β、η,通过式(1)建立极大似然函数,其表达式如下:
(9)
对该式左右两边取对数得:
(10)
根据偏导数,求取该式的极值,得到:
(11)
通过(1~11)式,可以得到β、η的估计值。
1.3 系统可靠性数学模型
系统是由相互作用和相互依赖的若干单元结合而成的具有特定功能的有机整体。文献[10]根据系统的特点,给出了多种可靠性建模方法,如可靠性框、BP网络可靠性模型、马尔可夫模型等。BP网络可靠性模型的缺点主要问题为:局部极小化问题,即训练可能得到不同的结果;网络结构的选择至今尚无统一而完整的理论指导,马尔可夫模型不适用于系统中长期的预测,而核电所用设备年限均较长。所以笔者所用的可靠性模型是通过可靠性框图建立的,即为预计或估算设备的可靠性所建立的可靠性框图和数学模型。可靠性框图由代表产品或功能的方框、逻辑关系、连线和节点组成。节点分为输入节点、输出节点和中间节点。可靠性数学模型主要有串联模型、并联模型、r/n(G)模型、旁联模型、桥联模型等。
系统的所有组成单元中任一单元的故障都会导致整个系统故障的系统称为串联系统。串联模型的可靠性框图见图1。

图1 串联模型可靠性框图
串联模型的可靠性数学模型为:
(12)
式中:Rs(t)为系统的可靠度;Ri(t)为单元的可靠度;n为组成系统的单元数。
串联系统的可靠度是各个单元可靠度的乘积,单元越多,系统可靠度越小。提高串联系统的可靠性主要可以从以下几个方面考虑:(1)尽可能减少串联单元个数;(2)提高单元可靠性,降低其故障率;(3)缩短工作时间t。
组成系统的所有单位发生故障时,系统才会发生故障的系统称为并联系统,并联模型是最简单的贮备模型。并联模型的可靠性框图见图2。

图2 并联模型可靠性框图
并联模型的可靠性数学模型为:
(13)
式中:Rs(t)为系统的可靠度;Ri(t)为单元的可靠度;n为组成系统的单元数。
并联系统与无贮备的单个单元相比,系统的可靠度明显提高,尤其是n=2时,可靠度的提高是更显著。但当并联单元过多时,可靠性提高速度大为减慢。
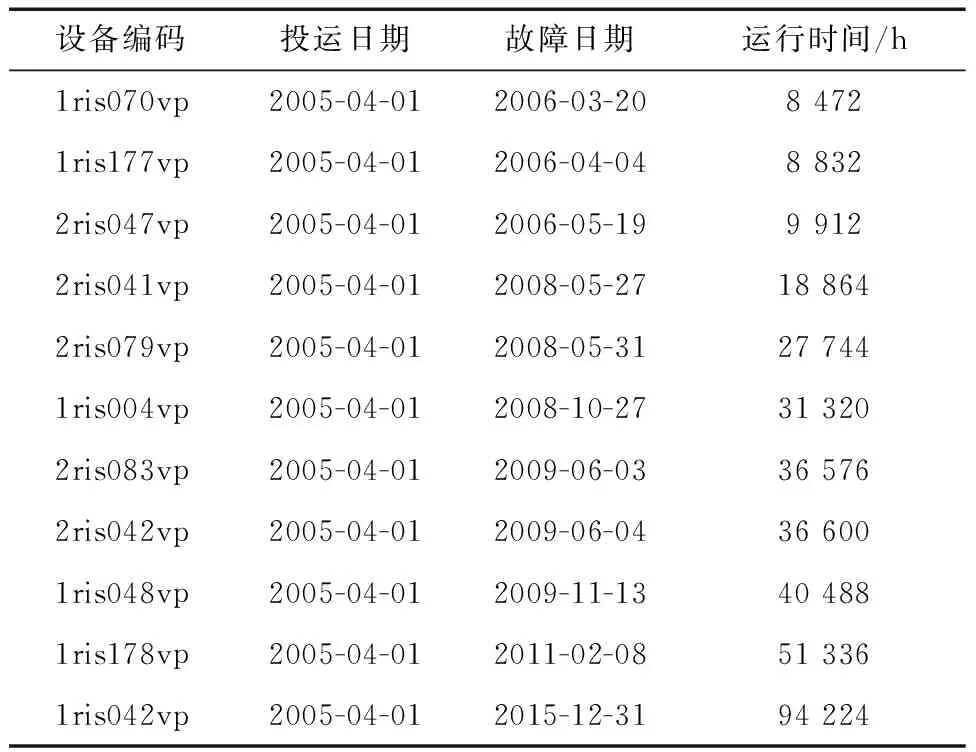
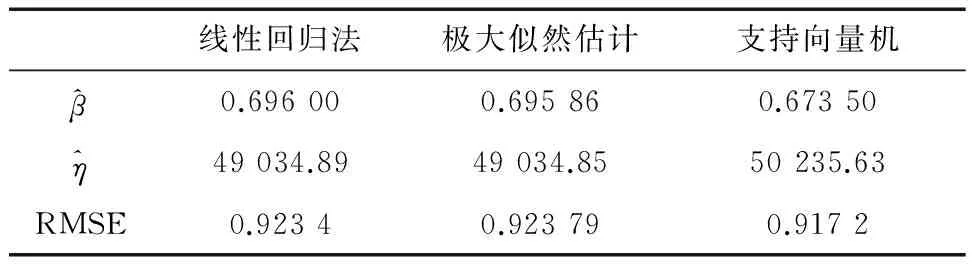
n个单元及一个表决器组成的表决系统,当表决器正常时,正常的单元数不小于r(1 图3 r/n(G)模型的可靠性框图 r/n(G)模型的可靠性数学模型为: (14) 式中:Rs(t)为系统的可靠度;Ri(t)为单元的可靠度;Rm为表决器的可靠度;n为组成系统的单元数。 在r/n(G)系统中,当n为奇数(令其为2k+1),且系统的正常单元数大于等于k+1时系统才正常,这样的系统称为多数表决系统。多数表决系统是r/n(G)系统的一种特例。三中取二系统是常用的表决系统。r/n(G)系统的MTBCF(致命故障间的任务时间)比并联系统小,比串联系统大。 系统可靠度流程见图4。 图4 系统流程图 首先将阀门、泵等原始小样本数据作为离散点,采用神经网络[11]的训练方法,得到扩充后的阀门、泵等数据;其次,采用威布尔公式,在阀门、泵等失效时间已知的条件下,通过中位秩公式[12],得到样本观测值的可靠度,利用线性回归、支持向量机、极大似然估计等可靠度计算模型找到最优估计参数,得到设备的失效率;最后,通过系统可靠度数学模型中的串联模型、并联模型、r/n(G)模型的使用,得到安全注入系统的可靠性。 3.1 设备可靠度 某电厂的安全注入系统的共有隔离阀10个、止回阀17个、流量控制阀7个、试验管线阀9个、低压安注泵2个、上充泵3个等设备。表1为部分止回阀数据。 表1 安全注入系统止回阀原始数据 表2为3种不同方法得出的止回阀的参数估计值。 表2 止回阀参数估计结果 表3为采用3种方法得出的参数计算的累计失效概率数值,由于数值点比较多,只给出了5个点的计算值。 表3 止回阀累计失效概率计算结果比较 图5为通过线性回归、极大似然估计和支向量机拟合的累计失效函数曲线。 图5 累计失效函数曲线图 从表2中可以得知:线性回归法和极大似然估计法的RMSE基本一致,比支持向量机法的RMSE要大,说明线性回归和极大似然估计的拟合效果要比支持向量机好。从图5中可以看出:线性回归法和极大似然估计法在失效时间较长时,拟合的准确性与支持向量机估计比较接近;在失效时间较短时,两者略有偏差。综上所述,在样本数量比较小的情况下,线性回归和极大似然略优于支持向量机估计,所以止回阀形状参数估计值为0.696,止回阀尺度参数估计值为49 034.89。 表4为隔离阀、流量控制阀、试验管线阀、低压安注泵及上充泵的参数估计结果。 表4 设备参数估计结果 根据RMSE的值越接近于1说明拟合效果越好的原则,并结合表4的数据进行分析可得到隔离阀、流量控制阀、试验管线阀、低压安注泵及上充泵的形状参数估计值和尺度参数估计值。 3.2 系统可靠性 安全注入系统分为三个部分:低压安注系统、高压安注系统、中压安注系统,笔者主要给出的是低压安注系统和高压安注系统的可靠度。按低压安全注入系统的功能可分为低压直接注入阶段、低压再循环注入阶段,按高压安全注入系统的功能分为高压冷管段直接注入阶段和高压冷热管段同时注入阶段,以下称为高压第一阶段和高压第二阶段。图6为不同年限的系统可靠度。 图6 安全注入系统可靠度趋势图 笔者以某国产核电机组为研究对象,通过收集其数据,采用威布尔分布模型,利用线性回归、支持向量机、极大似然估计3种拟合方法,得到各种设备的最优形状参数和尺度参数,结果表明线性回归的拟合效果最好。再利用串联模型、并联模型及r/n(G)模型得到安全注入系统的可靠度,分析出系统的可靠性在18个月前下降比较平稳,18个月后下降极快,其结果与核电工程的长燃料循环系统设备周期论证的结果相似。证明了线性回归拟合方法在核电安全注入系统可靠性研究方面的准确性。 [1] 陈济东. 大亚湾核电站系统及运行[M]. 北京: 原子能出版社,1994: 189-192. [2] SRIKRISHNA S,YADAVA G S,RAO P N. Reliability-centred maintenance applied to power plant auxiliaries[J]. Journal of Quality in Maintenance Engineering,2006,2(1): 3-14. [3] 尹晓伟. 基于贝叶斯网络的机械系统可靠性评估[D]. 沈阳: 东北大学,2008: 12. [4] 钱萍,陈文华,李星军,等. 产品可靠性的bootstrap回归统计分析方法[J]. 仪器仪表学报,2010,31(11): 2549-2554. [5] 王坤. 大型汽轮机转子寿命问题研究[D]. 武汉: 华中科技大学,2004. [6] 刘冰. 基于故障树的安注系统故障诊断专家系统研究[D]. 哈尔滨: 哈尔滨工程大学,2009. [7] 凌丹. 威布尔分布模型及其在机械可靠性中的应用研究[D]. 成都: 电子科技大学,2011: 12. [8] 马文·劳沙德. 系统可靠性理论: 模型统计方法及应用[M]. 郭强,王秋芳,刘树林,译. 2版. 北京: 国防工业出版社,2010. [9] 王小川,史峰,郁磊,等. MATLAB神经网络43个案例分析[M]. 北京: 北京航空航天大学出版社,2013: 102-125. [10] 曾声奎,赵廷弟,张建国,等. 系统可靠性设计分析教程[M]. 北京: 北京航空航天大学出版社,2001: 23-40. [11] 刘金琨. RBF神经网络自适应控制: MATLAB仿真[M]. 北京: 清华大学出版社,2014: 1-5. [12] 戴志辉,李芷筠,焦彦军,等. 基于BP神经网络的小样本失效数据下继电保护可靠性评估[J]. 电力自动化设备,2014,34(11): 129-134. Study on Reliability Assessment of Safety Injection System in Nuclear Power Plant Shen Wei,Lu Bin,Yang Bingqing,Jing Yajie,Zhu Xiaoliang (School of Energy and Environment,Southeast University,Nanjing 210096,China) To study the reliability of safety injection system,an equipment reliability calculation model was built for the system based on historical operation data of existing nuclear power units and with combination of numerical methods such as neural network,maximum likelihood estimation and support vector machine,so as to assess the reliability of the system by calculating the reliability of relevant equipment using reliability mathematical models. The feasibility of the method was verified by comparison with real-time operational data of nuclear power plants,which may serve as a reference for reliability assessment of safety injection systems in nuclear power plants. nuclear power; safety injection system; numerical method; mathematical model; reliability assessment 2016-09-06; 2016-12-06 沈 维(1991—),男,在读硕士研究生,研究方向为核电系统可靠性研究。 E-mail: 703334735@qq.com TK353.15 A 1671-086X(2017)04-0254-05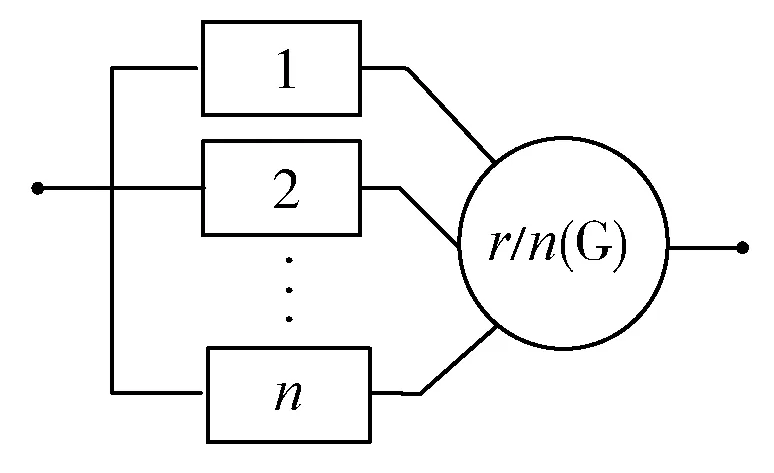
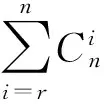
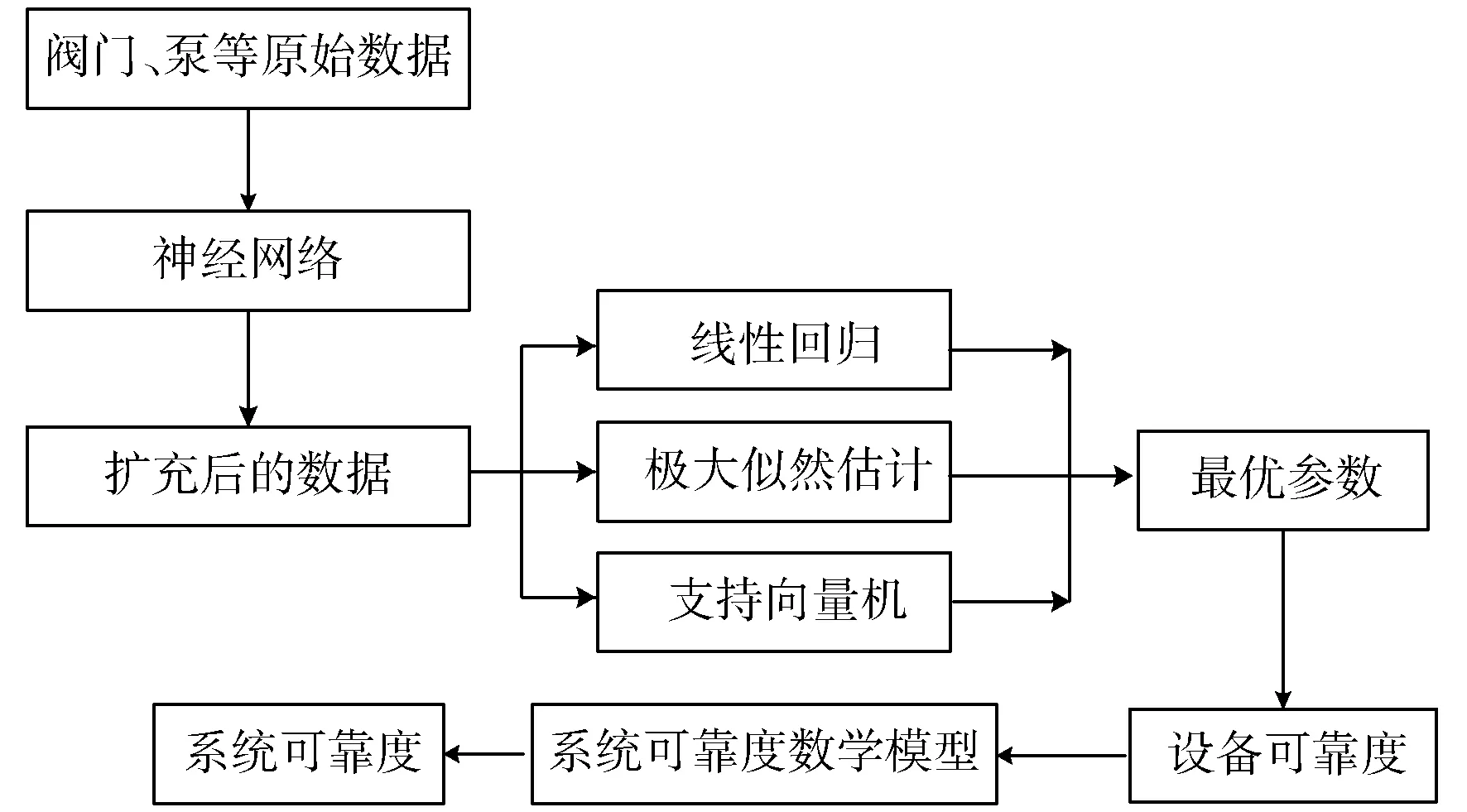
2 算法流程
3 计算结果

4 结语

