采用改进混合粒子群算法的热工过程模型参数辨识
陈 真,王明春,张雨飞
(东南大学 能源与环境学院,南京 210096)
研究与分析
采用改进混合粒子群算法的热工过程模型参数辨识
陈 真,王明春,张雨飞
(东南大学 能源与环境学院,南京 210096)
针对基本粒子群算法在求解过程中容易陷入局部最优解的问题,提出了一种基于遗传算法和模拟退火算法而改进的粒子群算法。引入遗传算法中的选择、杂交和变异,以及模拟退火机制的粒子群算法,在保持群体多样性的同时,提高全局搜索速度,并将改进的算法应用到热工过程模型参数的辨识,试验结果显示改进效果良好。
系统辨识; 粒子群算法; 遗传算法; 模拟退火算法
电力生产系统结构复杂,系统之间强耦合,难以试验建模,至今没有普遍适用的控制传递函数模型[1-2],根据现场运行参数直接求得热工过程的传递函数一直是控制领域研究的重要课题之一。近年来,群体智能(Swarm Intelligent)的快速发展及其在系统辨识中的应用,弥补了传统热工过程辨识方法的不足[3]。国内外学者对神经网络[4-6]、遗传算法[7-8]、蚁群算法[9]等群体智能算法在过程模型辨识的应用进行了广泛研究,其中粒子群优化 (PSO)算法是一种新兴的优化技术 ,其思想来源于人工生命和演化计算理论。PSO通过粒子追随自身最优解和整个种群的最优解来完成优化。该算法简单易实现,可调参数少,成为人们研究的热点算法之一[10]。然而通过实验证明,基本粒子群依赖信息共享和学习的最优解搜索方向机制[11]及种群特征控制的单一度量将逐渐弱化种群的多样性,且使得粒子个体的优势基因可能在进化中无法持续保持,从而导致在进化后期收敛速度下降出现早熟。
对此,笔者在基本粒子群算法中引入基于遗传算法中的选择机制,保留接种一部分较好的解,从而提高算法的收敛速度;同时算法融合了杂交、变异和模拟退火的思想,丰富粒子的多样性,使算法及时跳出局部最优,快速向全局最优收敛,克服基本粒子群算法的缺陷。将改进的算法应用到热工过程模型参数的辨识,试验结果显示改进效果良好。
1 算法介绍
基本粒子群优化算法是在1995年Kennedy和Eberhart模拟鸟群觅食过程中的迁徙和群集行为时提出的一种基于群体智能的演化计算技术。粒子群优化算法适用于求解非线性、不可微的复杂优化问题,其需要调节的参数不多,计算效率比传统随机方法高,且具有较好的鲁棒性。在粒子群算法中,用粒子的位置表示待优化问题的解,每个粒子性能的优劣程度取决于待优化问题目标函数确定的适应值,每个粒子由一个速度决定其飞行方向和速率的大小[12]。各粒子通过学习个体极值和全局极值逐渐向全局最优值靠近,根据下式更新自己的速度与位置。
(1)
(2)
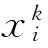
各个参数的选取原则如下:
粒子数N:粒子数的多少根据问题的复杂程度自行决定。对于一般的优化问题取20至40个粒子就完全可以得到很好的结果。
迭代次数k:取值和优化问题的复杂程度以及需要的运算精度有关。
惯性权重ω:一般取0.4至0.9之间。ω越小,算法局部收敛能力越强,却容易陷入局部最优;ω越大,算法全局搜索能力越强,却导致收敛速度慢。实验表明,ω约为0.729 8时,算法可以保证局部收敛能力的同时提高全局搜索能力。
学习因子c1和c2:学习因子使粒子具有自我总结和向群体中优秀个体学习的能力。一般取1至2.5之间,且c1等于c2。
2 算法改进
PSO算法参数少、收敛速度快、计算简便,但是在粒子搜索到接近最优粒子位置时,其速度会减小,粒子群趋向同一而失去多样性,这样使算法在迭代后期速度减慢且容易收敛到局部最优解。遗传算法中的选择、杂交和变异以及模拟退火算法具有独特的粒子多样性保持机制,与粒子群算法相结合,可以实现快速收敛到全局最优解。
混合粒子群算法流程图见图1。
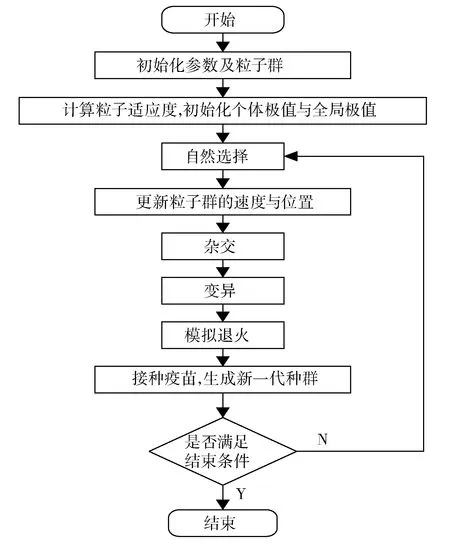
图1 混合粒子群算法流程图
混合算子设计:
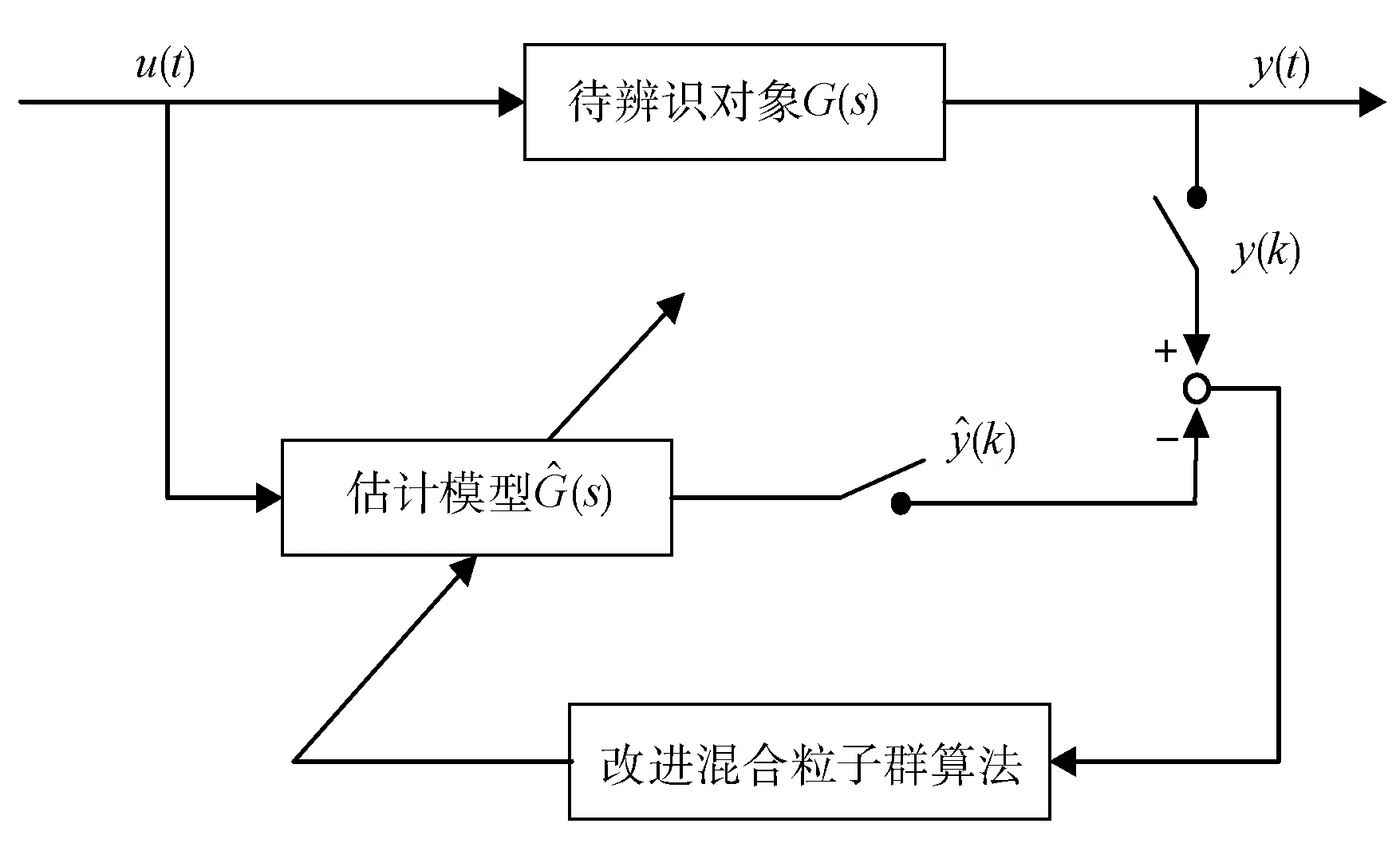
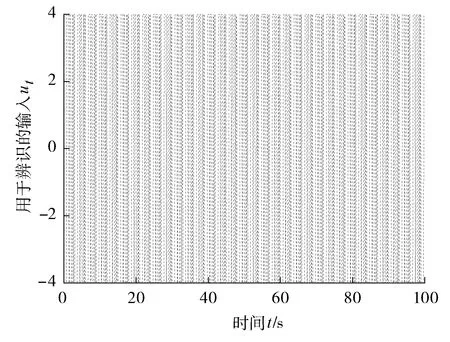
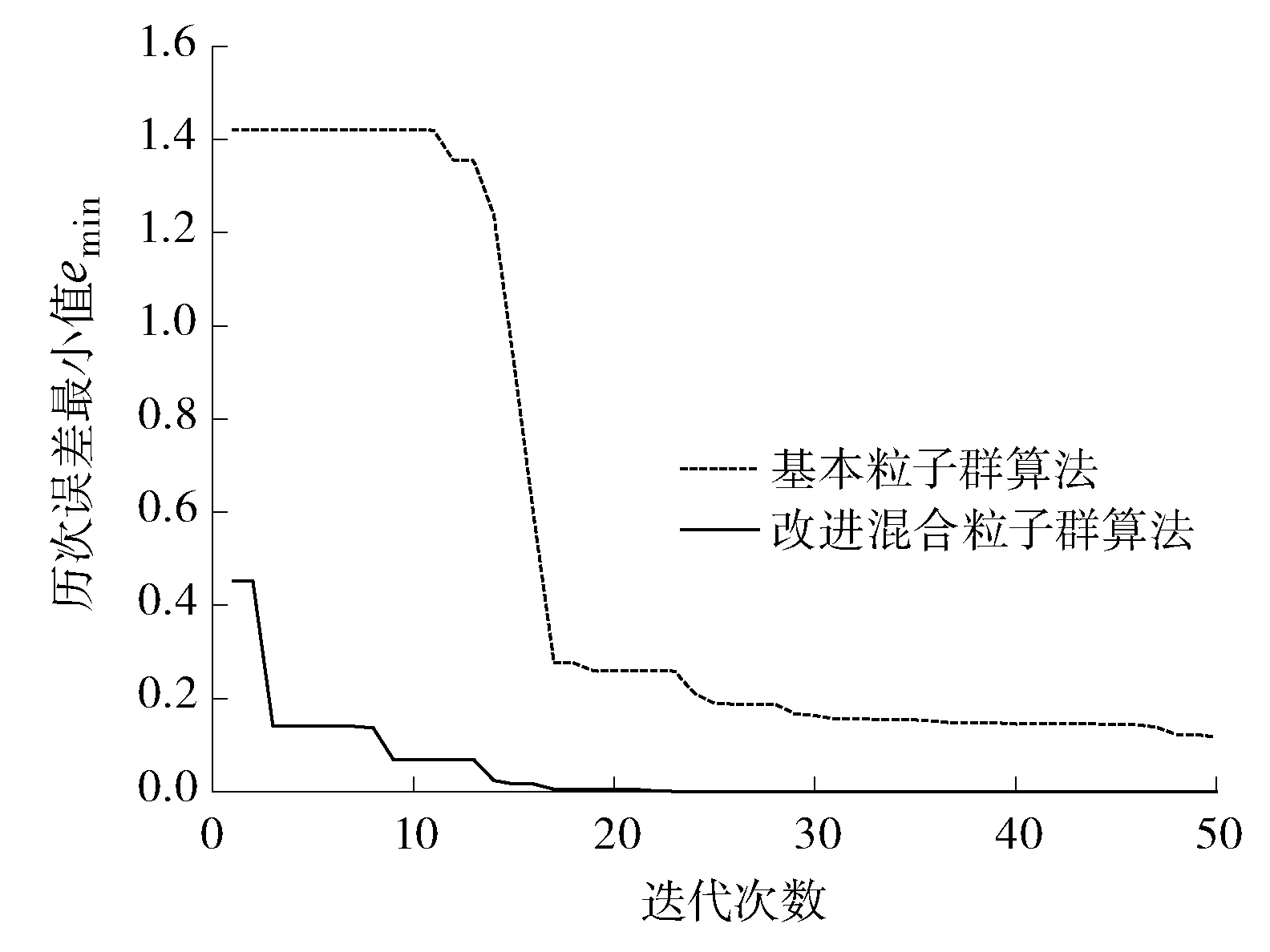
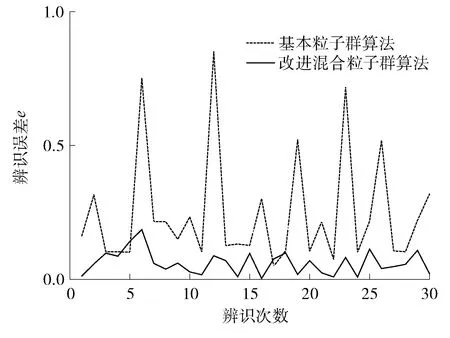
(1) 自然选择。每次迭代过程中将整个粒子群按适应度由大到小进行排序,选取前m(m (2) 杂交。根据杂交概率选取指定数量的粒子放入杂交池内,池中的粒子随机两两杂交产生同样数目的子代粒子,子代的位置和速度计算公式如下: (3) 式中:xc、vc分别为子代粒子的位置和速度;xp1、xp2为父代粒子的位置;vp1、vp2为父代粒子的速度;p是0到1之间的随机数。 (3) 自适应变异。采用自适应变异来保证选择复制后抗体的多样性,在迭代开始时,种群多样性较好,则变异概率Pm应较小;随着迭代的进行,种群中个体趋向同一,使Pm增加来改善种群多样性。Pm的表达式为: (4) 式中:Pmax、Pmin分别为最大、最小变异率;fmax为种群中最大适应度;favg为每代种群中的平均适应度;f为变异个体的适应度。 (4) 模拟退火。模拟退火算法在搜索过程中具有概率突跳的能力,能够有效地避免搜索过程陷入局部极小解。在退火过程中不但接受好的解,而且还以一定的概率接受差的解,同时这种概率受到温度参数的控制,其大小随着温度的下降而减小。根据下式确定当前温度下各pi的适配值: (5) vi,j(t+1)=φ{vi,j(t)+c1r1[pi,j-xi,j(t)]+ (6) xi,j(t+1)=xi,j(t)+vi,j(t+1) (7) 初始温度和退温方式对算法有一定的影响,一般采用下式的初温和退火方式: t0=f(pg)/ln5 (8) tk+1=λtk (9) (5) 接种疫苗与选择。将之前提取的疫苗与模拟退火后的粒子合并,按适应度由大到小排序,选取前N个粒子生成新一代种群。 3.1 辨识原理 图2 系统辨识结构图 定义指标函数为: (10) 3.2 模型结构 火电厂中绝大多数的热工过程都具有自平衡能力,一般可认为其为具有纯延迟的惯性系统,以二阶非线性动态模型为例,即: (11) 基于上述,共有四个未知参数:增益系数K、时间常数T1、T2和延迟时间τ。模型辨识的过程就是寻找最优参数K、T1、T2和τ,使指标函数式(10)最小的过程。 4.1 辨识步骤 为了验证改进混合粒子群算法的有效性,在Matlab上对热工过程的参数进行辨识,并和采用基本粒子群算法的参数辨识结果进行比较。构造热工过程模型如下: (12) 选取N=40,迭代次数为50,由于c1+c2必须大于4,c1=c2=2.05,此时C=4.1,收缩因子φ=0.729,这在形式上就等效于ω=0.729,c1=c2=1.494 45的基本PSO参数。使用e(n)记录每次迭代辨识误差最小值,算法在迭代次数到达50或e(n)等于0就停止执行。设待辨识参数K、T1、T2分布在[0,30]之间,τ分布在[0,1]之间。 首先运行模型测试程序,对象的输入信号采用8级线性反馈移位寄存器产生伪随机二进制序列(PRBS),及用于辨识的输入ut,考虑对系统的充分激励,幅值取为4,采样周期取0.1 s,运行时间t为100 s。伪随机二进制序列信号见图3。 图3 伪随机二进制序列信号 利用lsim函数求输出信号y,及y=lsim(G,ut,t),其中G为系统传递函数,从而得到用于辨识的模型测试数据。 4.2 结果分析 下两式分别为采用基本粒子群算法和改进混合粒子群算法的辨识结果: (13) (14) 式中:基本粒子群算法最终辨识误差e1为0.117;改进混合粒子群算法的最终辨识误差e2为5.94×10-6。 基本粒子群算法和改进混合粒子群算法的单位阶跃输出和实际输出对比见图4。结果表明:改进混合粒子群算法的单位阶跃输出和实际输出的拟合度更好。 图4 单位阶跃输出和实际输出对比图 基本粒子群算法与改进混合粒子群算法的辨识效果见图5。结果表明:由于引入了遗传算法中的选择、杂交和变异,以及模拟退火机制的粒子群算法,使粒子保持多样性的同时,提高全局搜索速度,且搜索后期避免了陷入局部极值。改进混合粒子群算法比基本粒子群算法能够获得更小的辨识误差以及更精确的模型参数。 图5 基本粒子群算法与改进混合粒子群算法辨识效果图 为验证算法的稳定性,对该对象重复进行了30次试验。图6为两种算法辨识效果的对比图。由图6可以看出:改进混合粒子群算法搜索到全局最优解的次数有15次,搜索概率为50%,且其他结果与最优解也很接近,基本满足工程实际需要;相比之下基本粒子群算法的搜索概率只有2%,其他搜索结果与全局最优解也相差甚远,效果不理想。由此表明:用改进混合粒子群算法进行目标参数辨识,辨识误差更低,误差波动范围更小,算法更加稳定。 图6 30次试验辨识误差e对比图 笔者提出一种基于遗传算法和模拟退火算法的改进粒子群优化算法。该算法是在基本粒子群算法基础上引入遗传算法中的选择、杂交和变异的思想,提高算法搜索速度并保持粒子多样性,避免陷入局部极值;利用模拟退火算法在搜索过程中具有概率突跳的能力,能够有效地避免搜索过程陷入局部极小解,提高了算法的精度。该方法克服了基本粒子群算法的缺陷,具有更高的寻优效率和逼近精度,在电厂热工过程参数辨识上具有一定的实用价值。 [1] 孙剑. 大型循环流化床锅炉燃烧系统特性与建模研究[D]. 北京: 华北电力大学(北京),2010. [2] 郝勇生,于冲,吴波. 先进控制算法在热工控制中的关键问题研究[J]. 发电设备,2013,27(2): 101-104. [3] 张洪涛,胡红丽,徐欣航,等. 基于粒子群算法的火电厂热工过程模型辨识[J]. 热力发电,2010,39(5): 59-61,81. [4] 张栾英,李瑞欣,秦志明,等. 采用模拟退火算法的Elman网络及在热工过程建模中的应用[J]. 中国电机工程学报,2005,25(11): 90-94. [5] 吴波,吴科,吕剑虹,等. 补偿递归模糊神经网络及在热工建模中的应用[J]. 东南大学学报: 自然科学版,2008,38(4): 668-673. [6] 米江,纪国宜. 基于改进BP神经网络的风机故障诊断研究[J]. 发电设备,2010,24(6): 430-434. [7] 刘长良,于希宁,姚万业,等. 基于遗传算法的火电厂热工过程模型辨识[J]. 中国电机工程学报,2003,23(3): 170-174. [8] 焦嵩鸣,韩璞,黄宇,等. 模糊量子遗传算法及其在热工过程模型辨识中的应用[J]. 中国电机工程学报,2007,27(5): 87-92. [9] 杨剑峰. 蚁群算法及其应用研究[D]. 杭州: 浙江大学,2007. [10] 杨维,李歧强. 粒子群优化算法综述[J]. 中国工程科学,2004,6(5): 87-94. [11] KENNEDY J. The particle swarm: social adaptation of knowledge[C]//Proceedings of IEEE International Conference on Evolutionary Computation. Indianapolis: IEEE,1997: 303-308. [12] 袁晓辉,王乘,张勇传,等. 粒子群优化算法在电力系统中的应用[J]. 电网技术,2004,28(19): 14-19. Model Identification of Thermal Process Based on Modified Hybrid Particle Swarm Optimization Chen Zhen,Wang Mingchun,Zhang Yufei (School of Energy and Environment,Southeast University,Nanjing 210096,China) To solve the problem of basic particle swarm optimization algorithm that is easy to fall into the local optimal solution,a modified hybrid particle swarm optimization algorithm was proposed based on the genetic algorithm and simulated annealing algorithm,i.e. introducing the selection,crossover and mutation in the genetic algorithm and the particle swarm optimization in the simulated annealing mechanism,which is able to maintain the diversity of particle swarms and improve the global evolution speed. Application results show that the modified hybrid particle swarm optimization algorithm has better effects compared with the basic particle swarm optimization algorithm. system identification; particle swarm optimization; genetic algorithm; simulated annealing algorithm 2016-09-18; 2016-10-17 陈 真(1990—),男,在读硕士研究生,研究方向为热工过程自动化控制。 E-mail: dian5566@qq.com TK321 A 1671-086X(2017)04-0223-04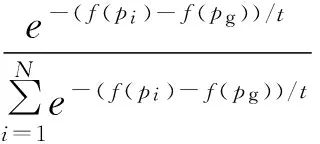
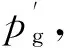
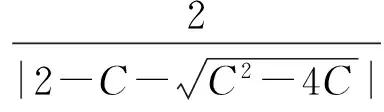
3 模型辨识
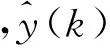
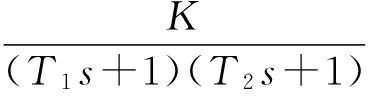
4 辨识仿真
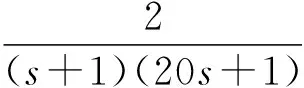
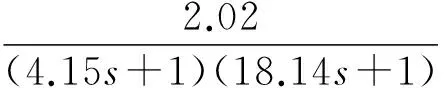
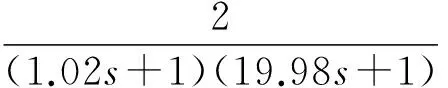

5 结语

