基于稳定性理论的张力腿平台横摇固有周期分析

吴 昊，林 焰

（大连理工大学 工业装备与结构分析国家重点实验室；运载工程与力学学部 船舶工程学院，辽宁大连 116024）

基于稳定性理论的张力腿平台横摇固有周期分析

吴 昊，林 焰

（大连理工大学 工业装备与结构分析国家重点实验室；运载工程与力学学部 船舶工程学院，辽宁大连 116024）

文章以稳定性理论为基础提出了一种张力腿平台横摇固有周期计算模型，分析了横摇临界角对平台横摇稳定性的影响，并将其应用于分析平台设计参数对横摇固有周期的影响。提出在一个横摇周期里，最后稳定横摇临界角对应的时间历程为1/4横摇固有周期这一假设，基于此假设，编制计算机计算程序，计算横摇运动中每一个横摇角，判断其稳定性，找出一个横摇周期内最后稳定横摇临界角对应的时间历程，求解横摇运动固有周期。考虑两种横摇阻尼情况，计算不同初始横摇角、横摇下沉位移、张力腱长度、平台重量和横摇阻尼的横摇固有周期，论证了平台设计参数对横摇固有周期的影响。该计算模型克服了从结构角度计算固有周期工作量大、计算周期长、计算结果不可靠的弱点，使横摇固有周期计算简单、有效。通过与不考虑横摇阻尼的情况对比，分析了横摇阻尼对横摇固有周期的影响。可以快速计算处于设计阶段或者已服役张力腿平台横摇固有周期。结合一型设计中的张力腿平台，应用文中提出的横摇固有周期计算模型对该平台进行了横摇固有周期的计算，并且分析了平台参数对横摇固有周期的影响。结果表明该方法可以对张力腿平台横摇固有周期进行快速计算。并可推广应用于其它海上结构物的横摇固有周期计算。

张力腿平台；横摇；稳定性；临界角；固有周期

0 引 言

石油是经济的血液，拥有充足的油气资源，并且保证油气资源的稳定供给，是经济平稳发展的必要条件。进入21世纪以来，随着社会和经济的发展，世界已经逐渐步入能源稀缺时代。陆上资源开发难度越来越大，许多国家把目光转向海洋[1]。海洋环境的复杂多变，波浪和风的无序性，对海洋结构物的运动有很大影响，甚至威胁它们的安全。海洋环境施加在海洋结构物上的载荷影响着海洋结构物的运动。海洋结构物在海洋中有6个自由度的运动，分别是：ξ1纵荡、ξ2升沉、ξ3横荡、ξ4横摇、ξ5首摇和ξ6纵摇。横摇运动对于张力腿平台在作业工况和自存工况的稳定性有着重要影响。对于张力腿平台，水平面结构近似对称，在不考虑横摇和纵摇惯性矩不同的情况下，ξ4横摇运动和ξ6纵摇运动近似相同。本文主要讨论ξ4横摇运动。

1 研究现状

Virgin[2]描述了一个数值和现象学相结合的方法来分析横摇运动，非线性阻尼和复原力臂特性。参照定性预测技术对周期运动的稳定性，特别是倾覆的可能性进行了探索。规则横浪中混沌运动现象是一个新的特征，应该引起设计师的兴趣。例如摄动技术，利用动力学系统理论指导下的数值模拟检测混沌现象是正当的，这是传统定量方法的局限性。Soliman等[3]做了一个经典的研究。该研究提出了半经验非线性微分方程的稳态和瞬态解，并将其应用于模拟在海军建造文献中被广泛讨论的两艘沉船的共振横摇运动。起始条件的空间安全区域的分析表明，瞬态倾覆可以在最后稳定运动状态是稳定性丧失的对应波高的一小部分时发生。该安全区域在中部区域的侵蚀非常突然，这意味着瞬间倾覆可能是一个合理的可重复的现象，提供了一种新的方法来量化船在波浪中的稳定性。Lin等[4]开发了随机分析程序，研究受到随机噪声干扰的周期性激励作用的混沌横摇运动和船舶倾覆的性质。数值结果表明，在噪声的情况下，船舶所有在异宿轨道附近的横摇运动轨迹将最终导致倾覆。Taylan[5]利用静稳性和非线性动力学稳定性提出了被称为“稳性储备”或者“稳性裕度”两种相对不同的方法，分析船舶流体力学。为了实现这个目的，横浪中的非线性横摇模型已经实现。根据分析的结果，提出了改善在海浪中船舶稳定性的建议。谷家扬等[6]对随机波浪下的张力腿平台耦合响应进了研究。用龙格—库塔方法解时域运动方程。Jonswap谱通过线性插值模拟随机波浪和流，风谱使用NPD谱。用蒙特卡罗方法模拟随机波和风的波动。

许多学者对张力腿平台在海洋中的运动进行了广泛而富有成效的研究。横摇运动和倾覆的研究主要集中在船舶领域，海洋结构物的横摇运动和倾覆的研究很少，特别是关于张力腿平台的横摇运动和倾覆研究很少。本文主要研究张力腿平台横摇稳定性以及横摇固有周期。

2 横摇运动模型

张力腿平台在海洋中受到外界载荷的激励作用，产生ξ1纵荡、ξ2升沉、ξ3横荡、ξ4横摇、ξ5首摇和ξ6纵摇六个自由度的运动。

对于张力腿平台，张力腱的预张紧力平衡平台浮力与重力之间的差值，横摇运动往往伴随横荡运动，横摇运动会引起平台升沉运动。张力腿平台水平面的结构近似对称，不考虑横摇和纵摇惯性矩不同，ξ4横摇运动和ξ6纵摇运动近似相同。本文主要研究ξ4横摇运动。海洋结构物受到波浪和风等外界载荷扰动，一般非线性微分横摇方程如下：

式中：Θ是横摇角，rad；I44是横摇惯性力矩，N·m；A44是水动力引起的附加惯性力矩，N·m；b1，b2，c1，c2，c3，c4和c5是系数；M（）t是扰动力矩，N·m；WM是风倾力矩，N·m。

3 张力腿平台横摇固有周期计算

张力腿平台在海洋中受到浮力、重力和张力腱的预张紧力的作用产生ξ1纵荡、ξ2升沉、ξ3横荡、ξ4横摇、ξ5首摇和ξ6纵摇六个自由度的运动。平台所受浮力与排开水的体积成正比，平台在海洋中的浮力体为半浸没的圆柱形立柱和全浸没的长方形横撑，是规则体，正常作业工况下排水体积与平台升沉位移成正比，所以可以用弹簧k表示平台升沉位移与浮力之间的关系，平台位移向下，浮力增大，等效弹簧拉力增大；平台位移向上，浮力减小，等效弹簧拉力减小。正常作业工况下张力腱张紧，张力腱内部存在预张紧力，考虑张力腱弹性系数为线形，预张紧力与拉伸位移成正比，即预张紧力与平台升沉位移成正比，所以可以用弹簧k1表示平台升沉位移与预张紧力之间的关系，平台位移向下，预张紧程度减小，张力腱的预张紧力减小；平台位移向上，预张紧程度增大，张力腱的预张紧力变大。张力腿平台在四组张力腱的约束下在海洋中运动，运动中张力腱长度变化与张力腱原长相比很小，可以忽略运动中的四组张力腱长度的不同。横摇运动是绕轴转动，平台水平面近似对称，横摇运动中有相同横摇转角的两组张力腱拉伸位移近似相同，横摇转角两侧的两组张力腱拉伸位移不同，所以可将张力腿平台横摇运动所受外力简化为两组拉伸位移不同的弹簧k1和弹簧k。

将张力腿平台简化为质点M，两组弹簧k1等效平台所受张力腱的预张紧力，弹簧k等效平台所受浮力。所以可以用质点M、两组弹簧k1和弹簧k模拟张力腿平台真实横摇运动和受力。张力腿平台横摇运动模型如图1所示。本文分析两种横摇运动，一种是考虑横摇阻尼的横摇运动，另一种是不考虑横摇阻尼的横摇运动。

在图1建立的横摇运动模型基础上，应用稳定性理论中临界点、中心点和鞍状点概念，提出一种张力腿平台横摇固有周期计算模型。该横摇固有周期计算模型原理为：在一个横摇运动周期的前1/4历程，横摇过程的任何一个角度都可能为横摇临界角。横摇临界角可能为稳定的中心点，也可能为不稳定的鞍状点。在稳定性理论中，一个横摇运动周期内，横摇临界角如果为中心点，横摇运动在此时刻稳定，继续运动到下一时刻；如果下一时刻横摇临界角为鞍状点，横摇运动在此时刻不稳定，说明此时刻横摇运动的前1/4周期已结束。基于此横摇运动稳定性分析，提出在一个横摇周期里，最后稳定横摇临界角对应的时间历程为1/4横摇固有周期这一假设。基于此假设，编制计算机计算程序，计算横摇运动中每一个横摇角，判断其稳定性，找出一个横摇周期内最后稳定横摇临界角对应的时间历程，求解横摇运动固有周期。张力腿平台横摇固有周期计算模型计算流程如下：

（1）建立张力腿平台横摇运动方程；

（2）求解横摇临界角，判断临界角的稳定性；

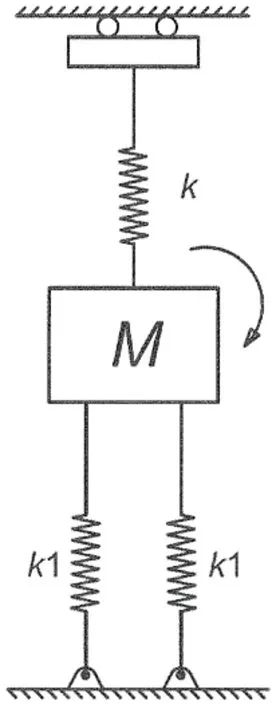
图1 张力腿平台横摇运动模型Fig.1 TLP roll motion model

（3）确定横摇临界角最终稳定时间；

（4）横摇临界角最终稳定时间为一次横摇运动的1/4固有周期，求解张力腿平台横摇固有周期。张力腿平台横摇固有周期计算流程图如图2所示。

3.1 考虑横摇阻尼的张力腿平台横摇运动

对于张力腿平台横摇运动，横摇位移正比于横摇角，横摇阻尼为非线性。二次非线性是最简单的高阶非线性，假设平台横摇阻尼与横摇角速度的平方成正比。

3.1.1 张力腿平台横摇运动方程及

临界角计算

考虑二次非线性横摇阻尼，建立张力腿平台横摇方程，如下：

图2 张力腿平台横摇固有周期计算流程图Fig.2 Flowchartofrolling naturalperiod of TLP

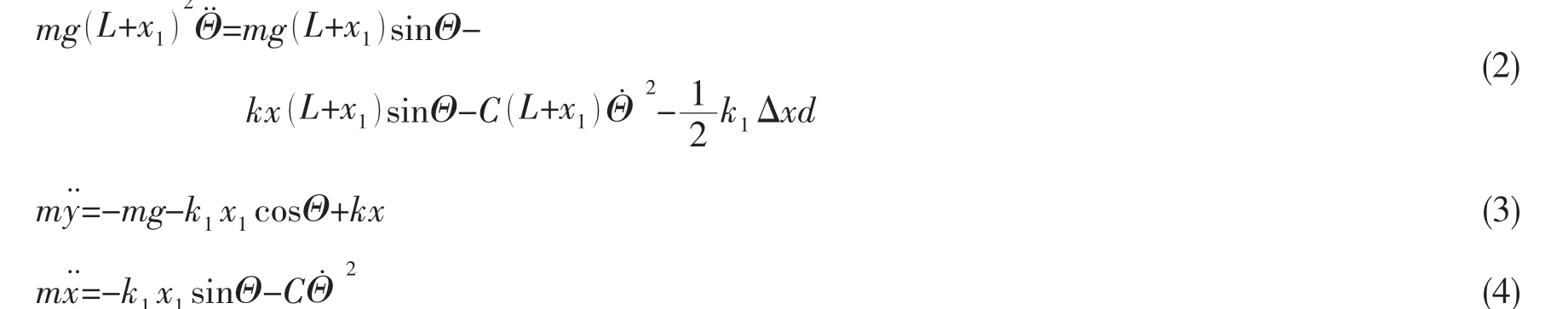
式中：C为横摇阻尼系数，N/rad；k为浮力系数，N/m；k1为张力腱弹性系数，N/m；x为平台横摇下沉位移，m；t为时间，s；△x为横摇引起的两组张力腱长度差值，m；d为两组张力腱水平距离，m；L为张力腱长度，m；G=mg为平台重量，N。

张力腿平台张力腱长度远远大于△x，忽略各组张力腱长度不同对横摇运动的影响。通过横摇方程求解横摇角θ。在临界角时，横摇角θ的角速度Θ˙为0，角加速度Θ¨最大。令

令f=0，求临界角。解得临界角方程为：

横摇角Θ是时间的函数。横摇角Θ随着横摇运动在时间上累积。解得横摇临界角θ为：

式中：a为初始横摇角系数，即通解常数。t为时间，s。

初始横摇角系数a决定了平台在横摇初始时刻的位置，和初始时刻的横摇角速度。由横摇角表达式可知角加速度为常数，所以初始横摇角系数a不决定角加速度。临界角θ为通解，需要初始边界条件确定初始横摇角系数a，解得特解。任何位置都可以是平台在横摇前的初始位置，所以不能解得初始横摇角系数a具体数值。由初始时刻横摇角小于90°解得a∈ ［-2.506 6，2.5066］。且初始横摇角系数a越接近0，初始横摇角越小。

3.1.2 张力腿平台横摇临界角稳定性的判断

f对θ求导，得：

本文结合流花16-2张力腿平台，论证张力腿平台横摇稳定性和计算横摇固有周期。平台重量及载荷约为43 188t，立柱结构尺寸如图3所示。

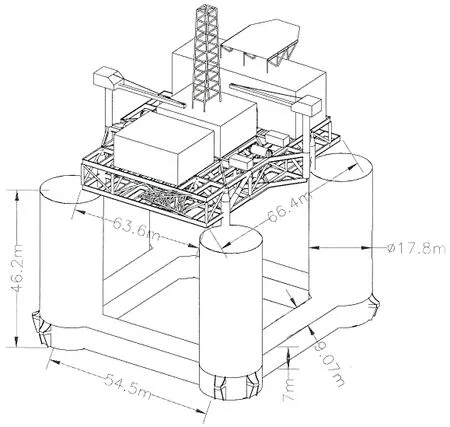
图3 张力腿平台结构尺寸Fig.3 Size of TLP

图4 张力腿平台横摇临界角时间历程数值模拟曲线（L=500 m，x=1 m）Fig.4 TLP times courses numerical simulation of parametric roll critical points(L=500 m,x=1 m)

张力腿平台横摇临界角时间历程数值模拟曲线图，如图4和图5所示。

固定横摇下沉位移x，改变初始横摇角系数a。

固定初始横摇角系数a，改变横摇下沉位移x。

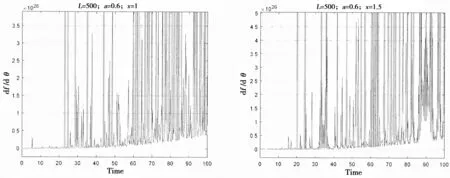
图5 张力腿平台横摇临界角时间历程数值模拟曲线 （L=500 m，a=0.6）Fig.5 TLP times courses numerical simulation of parametric roll critical points(L=500 m,a=0.6)

从图4和图5数值模拟曲线中可以看到，有限时间内，随着时间的累积，横摇角的在负值与正值之间震荡。说明横摇临界角在中心点和鞍状点之间转换，横摇临界角在稳定与不稳定之间转换。平台不能在平衡位置周期性横摇，横摇路径随着外界扰动的不同而不同。横摇初始阶段，值为负值且近似为0，说明平台处于外界力干扰很小的稳定状态，其横摇状态主要由稍后的外界扰动作用决定。随着横摇过程在时间上的累积，在正值与负值之间震荡，横摇临界角在中心点和鞍状点之间转换，横摇临界角在稳定与不稳定之间转换，平台可能在不是平衡位置的某点达到平衡。当时间经过累积后，大部分工况的横摇角的这些点为鞍状点，平台横摇不稳定，平台对应的运动状态可能已经倾覆。所以张力腿平台的横摇运动非常复杂，不能用理论公式预测其平衡位置，只能用频域或者时域的方法来模拟横摇运动状态。

3.1.3张力腿平台横摇固有周期计算

在单自由度质点弹簧运动系统里，质点的运动终止点为回复力最大的时刻。在时间历程中，当质点的加速度达到最大值或者局部极大值时，此刻质点速度最小，等于零，质点位移为最大。对于张力腿平台的一次横摇运动，横摇角加速度为最大值或者局部极大值时，此刻平台横摇角速度为最小，等于零，横摇角最大，平台横摇运动达到最大幅值，此时间历程为平台横摇运动周期。其所对应的时间即为横摇运动固有周期。由计算机程序绘制的横摇临界角时间历程数值模拟曲线图，当达到此时间历程中最后一个负值时，说明横摇达到最后的稳定点，该点可作为横摇的固有周期处理。由此可求得平台的横摇固有周期。横摇固有周期T计算公式如下：

式中：T为横摇固有周期，s；tln为横摇临界角时间历程数值模拟曲线的时间历程中最后一个负值时刻，s。

3.1.4 张力腿平台设计参数对横摇固有周期的影响

由横摇固有周期T计算公式可获得不同平台参数下横摇固有周期数值。

改变平台设计参数，求得平台横摇最后稳定点的时间历程，求解横摇固有周期，绘出不同平台参数对横摇固有周期的影响曲线。经过分析，对张力腿平台横摇固有周期有影响的设计参数有：初始横摇角、横摇下沉位移、张力腱长度、平台重量和横摇阻尼。

改变平台横摇下沉位移x，得到不同初始横摇角系数a值下最后稳定点对应的时间历程曲线，如图6所示。

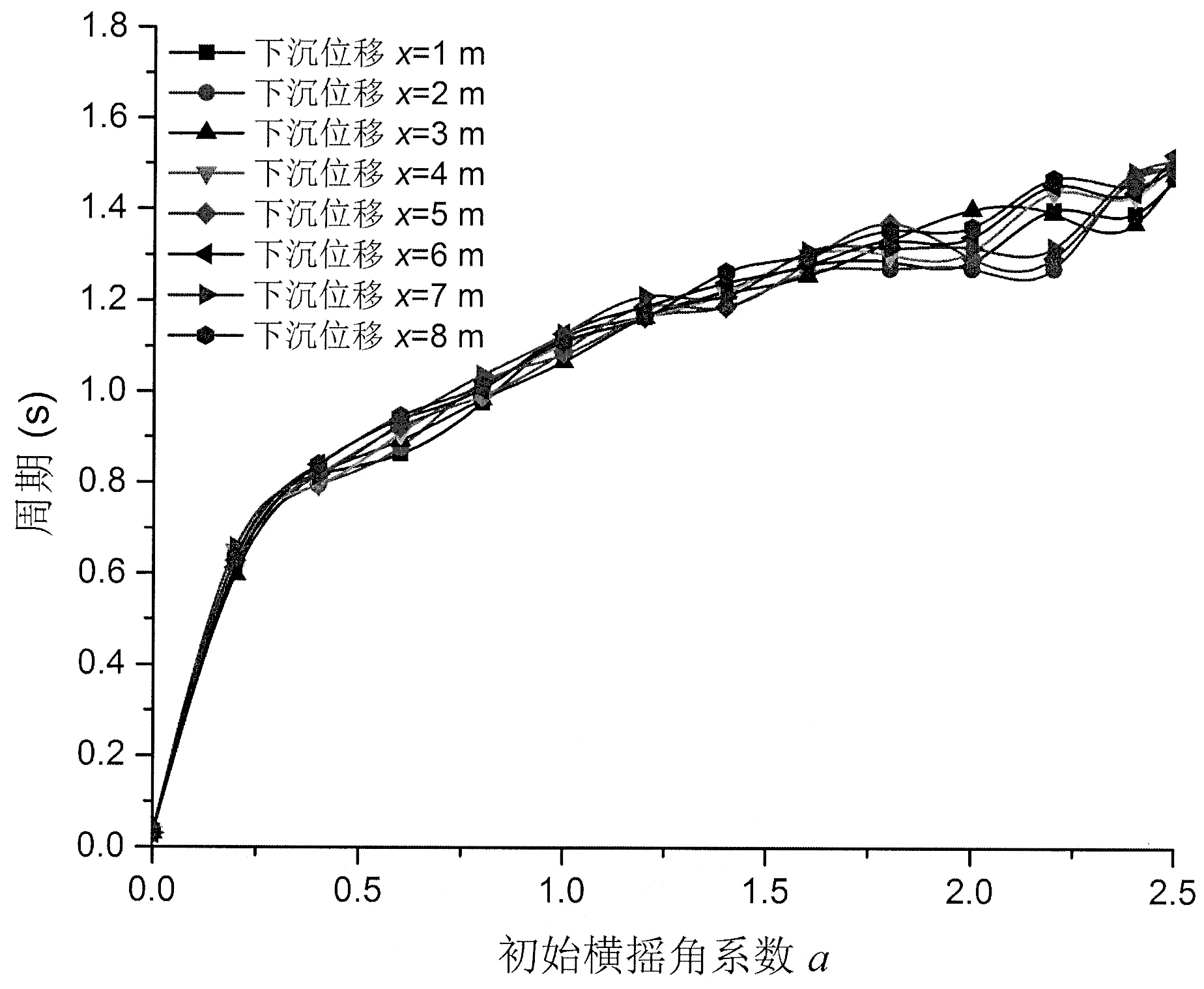
图6 不同平台横摇下沉位移x对横摇固有周期影响曲线Fig.6 The effects of different displacement of roll subsidence x on rolling natural period

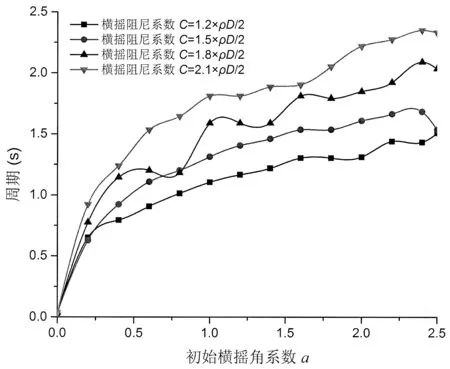
从图6中可以看出，随着初始横摇角系数a的增大，横摇固有周期逐渐增大。当a=0，横摇固有周期很小，但是不为零。当00.2时，横摇固有周期随初始横摇角的增大而增大，增长速率变缓，不同平台横摇下沉位移对应的固有周期差异开始显现。当0

改变平台张力腱长度L，得到不同初始横摇角系数a值下最后稳定点对应的时间历程曲线，如图7所示。

图7 不同张力腱长度对横摇固有周期影响曲线Fig.7 The effects ofdifferentlength oftendon L on rolling natural period

从图7中可以看出，随着初始横摇角系数a的增大，横摇固有周期逐渐增大。张力腱长度对横摇固有周期影响很小。当00.2时，横摇固有周期随初始横摇角的增大而增大，增长速率变缓，斜率小于0

改变平台重量G，得到不同初始横摇角系数a值下最后稳定点对应的时间历程曲线，如图8所示。

从图8中可以看出，随着初始横摇角系数a的增大，横摇固有周期逐渐增大。平台重量对横摇固有周期影响比较大。当0

改变平台横摇阻尼系数C，得到不同初始横摇角系数a值下最后稳定点对应的时间历程曲线，如图9所示。

从图9中可以看出，随着初始横摇角系数a的增大，横摇固有周期逐渐增大。横摇阻尼系数C对横摇固有周期影响很大。当0

图8 不同平台重量对横摇固有周期影响曲线Fig.8 The effects of different weight G on rolling natural period

图9 不同横摇阻尼系数对横摇固有周期影响曲线Fig.9 The effects of different roll damping coefficient C on rolling natural period

3.2 考虑无横摇阻尼的张力腿平台横摇运动

3.2.1 张力腿平台横摇运动方程及临界角计算当平台横摇没有阻尼时，建立张力腿平台横摇方程，如下：

式中：k为浮力系数，N/m；k1为张力腱弹性系数，N/m；x为平台横摇下沉位移，m；t为时间，s；△x为横摇引起的两组张力腱长度差值，m；d为两组张力腱水平距离，m；L为张力腱长度，m；G=mg为平台重量，N。

张力腿平台张力腱长度远远大于△x，忽略各组张力腱长度不同对横摇运动的影响。通过横摇公式求解横摇角θ。在临界角时，横摇角θ的角速度Θ˙为0，角加速度Θ¨最大。令

令f=0，求临界角。

解得临界角方程为：

横摇角θ是时间的函数。由于横摇运动，横摇角θ是时间的累积量。解得横摇临界角θ为

式中：a为初始横摇角系数，即通解常数；t为时间，s。

初始横摇角系数a决定了张力腿平台在横摇初始时刻的位置，和初始时刻的横摇角速度。由横摇角表达式可知角加速度为常数，所以初始横摇角系数a不决定角加速度。横摇临界角θ为通解，需要初始边界条件确定初始横摇角系数a，解得特解。任何位置都可以是平台在横摇前的初始位置，所以不能解得初始横摇角系数a具体数值。初始横摇角系数a越接近0，初始横摇角越小。

3.2.2 张力腿平台横摇临界角稳定性的判断

f对θ求导，得：

3.2.3 张力腿平台横摇固有周期计算

4 结 论

本文以稳定性理论为基础提出了一种张力腿平台横摇固有周期计算模型，分析了横摇临界角对平台横摇稳定性的影响，并将其应用于分析平台参数对横摇固有周期的影响。提出在一个横摇周期里，最后稳定横摇临界角对应的时间历程为1/4横摇固有周期这一假设，基于此假设，编制计算机计算程序，计算横摇运动中每一个横摇角，判断其稳定性，找出一个横摇周期内最后稳定横摇临界角对应的时间历程，求解横摇运动固有周期。结合一型设计中的张力腿平台，考虑两种横摇阻尼情况，计算不同初始横摇角、横摇下沉位移、张力腱长度、平台重量、横摇阻尼的横摇固有周期，论证了平台参数对横摇固有周期的影响，对平台的设计提出了建设性的意见。论证结论如下：

（1）此型张力腿平台横摇固有周期小于2.4s。

（2）论证了平台参数对横摇固有周期的影响。论证了平台横摇下沉位移，初始横摇角，张力腱长度，平台重量，阻尼系数对横摇固有周期的影响。

a.平台横摇下沉位移的变化对横摇固有周期的影响较小。初始横摇角直接影响横摇固有周期。

b.张力腱长度对横摇固有周期有影响，但影响不大。

c.平台重量对横摇固有周期影响较大。

d.横摇阻尼对横摇固有周期影响很大。

（3）利用平台重量、横摇阻尼对横摇固有周期影响不稳定的特性，可以有效避开环境载荷频率与平台自身频率的重合，减少共振的发生。

该横摇固有周期计算模型克服了从结构角度计算固有周期工作量大、计算周期长、计算结果不可靠的弱点，使横摇固有周期计算简单、有效。经过与不考虑横摇阻尼的情况对比，分析了横摇阻尼对横摇固有周期的影响。可以快速计算处于设计阶段或者已服役张力腿平台横摇固有周期。该方法也可以应用于其他海洋结构物横摇固有周期计算。

[1]吴 昊,林 焰.张力腿平台系泊风险评估方法研究[J].船舶力学,2016,20(5)：11-14. Wu Hao,Lin Yan.The risk assessment of mooring for tension leg platform[J].Journal of Ship Mechanics,2016,20(5)：11-14..

[2]Virgin L N.The nonlinear rolling response of a vessel including chaotic motions leading to capsize in regular seas[J].Applied Ocean Research,1987,9(2)：89-95.

[3]Soliman M S,Thompson J M.Transient and steady state analysis of capsize phenomena[J].Applied Ocean Research,1991,13(2)：82-92.

[4]Lin H,Yim S C.Chaotic roll motion and capsize of ships under periodic excitation with random noise[J].Applied Ocean Research,1995,17(3)：185-204.

[5]Taylan M.Static and dynamic aspects of a capsize phenomenon[J].Ocean Engineering,2003,30(3)：331-50.

[6]Gu J,Yang J,Lv H.Studies of TLP dynamic response under wind,waves and current[J].China Ocean Engineering,2012, 26：363-378.

Analysis rolling natural period for tension leg platform based on stability theory

WU Hao,LIN Yan
(School of Naval Architecture Engineering,Faculty of Vehicle Engineering and Mechanics,State Key Laboratory of Structural Analysis for Industrial Equipment,Dalian University of Technology,Dalian 116024,China)

A calculation model was established to research on rolling natural period of Tension Leg Platform (TLP)based on stability theory.The effects of roll critical points on rolling stability and effects of parameters of TLP on rolling natural period were analyzed.And an assumption was put forward that in one rolling motion,times courses corresponding the last stable roll critical point condition is a1/4cycle process.Based on the assumption,computer programs were built to calculate arbitrary roll angle,and used to estimate stability of arbitrary roll angles,so that times courses corresponding the last stable roll critical point in one rolling motion were found.So it can obtain rolling natural period.Considering two conditions of damping, this paper calculated rolling natural period under different initial roll angle,displacement of roll subsidence, length of tendon,weight and roll damping coefficient and demonstrated the influences of parameters of TLP on rolling natural period.The model is simple and effective to support fast estimating rolling natural period whether TLP is in designed stage or in service and avoid to obtain rolling natural period complicated withstructural theory.The influences of roll damping on rolling natural period were demonstrated.Based on a TLP which is in design stage,the rolling natural period was obtained with the established model.In this case,the influence of parameters of TLP on rolling natural period was found.Results show that the model is simple and effective to support fast estimating rolling natural period.This model can also apply to other marine structures to calculate rolling natural period.

Tension Leg Platform;roll;stability;critical point;natural period

P756.2

A

10.3969/j.issn.1007-7294.2017.07.006

1007-7294（2017）07-0842-14

2017-02-28

吴 昊（1989-），男，博士研究生；

林 焰（1963-），男，教授，博士生导师，E-mail：linyanly@dlut.edu.cn。